易逝性食品的温度控制及定价研究

刘温温，冯 琳，何亚兰

(天津大学系统工程研究所，天津 300072)

所谓易逝品是指那些有固定生命周期的产品，例如电子产品、服装、食品等。通常可将易逝品分为两类:一类是受产品价值制约的易逝品，例如电影票;另一类是受产品质量制约的易逝品，例如食品［1］。

大多企业经营的主要目标是最大化产品收益，而产品价格和质量又是影响其收益的两个主要因素。一般来说，顾客需求受价格影响较为明显，价格的降低会有效刺激销量，但企业销售单位产品的利润也会随之降低;反之价格的提升会削弱顾客的购买意愿，同时会增加企业的库存负担，尤其对于主营易逝品的企业，库存衰减所带来的损失会增大。随着人们生活水平的不断改善，产品的质量也成为顾客是否选择该产品的主要标准之一。通常情况下，产品质量由生命周期表征，而生命周期又主要受仓储温度影响。企业为了减少产品损耗带来的损失，往往会采取相应措施来控制仓储温度以延长其生命周期。然而，这些温度控制手段又会诱发一定的成本，如何更好地权衡收益与控制成本之间的关系，找到一个最优仓储温度，与企业的利益息息相关。

在产品定价方面，合理的定价策略不但会吸引更多的消费者，也会有效地刺激需求，是企业提高利润的重要手段［2－6］。YAO 等［7］分析了价格敏感系数与顾客需求之间的关系。SCHÜTZE［8］将定价策略主要分为3类，即动态定价，静态定价和混合定价。在质量控制方面，LABUZA［9］、RONG 等［10］以及 WANG 和 LI［11］介绍了一个质量衰减模型，并提出需要在整个供应链中考虑产品质量。面对即将到期的产品和新产品，在销售价格相差不大的情况下，顾客往往会青睐于后者。目前，大多数企业已经逐渐认识到产品质量在分销计划以及再制造过程中的重要性［12－13］。在温度控制方面，对于易逝性食品，产品质量受温度影响较为明显。目前，已有很多学者考虑采取温度控制的手段来提升企业竞争力［14－15］。一般情况下，仓储温度越低，产品的生命周期越长，较长的生命周期可为产品带来更大的定价空间。考虑到在众多易逝品中，食品对温度的变化较为敏感，因此笔者将其作为主要的研究对象。在考虑温度的影响时，AKKERMAN等［16］提出了在食品供应链中，控制温度可分为3类:冷冻、冷藏和常温保存。但是，在具体考虑每一类食品供应链时，大多研究均把温度假设为离散变量，从这些离散取值中挑选能够使利润达到最大值的最优温度，例如CORZO 等［17］和 TSIRONI等［18］通过较大容量的样本实验来获得最优温度。RONG等通过给定的数学规划方法得到最优温度。

然而，当考虑企业的收益最大时，目前还没有一个统一的标准来获得最优温度，也很少有学者将温度控制与产品定价结合考虑。因此，笔者在前人研究的基础上，从更加切合实际的角度出发，将温度作为连续变量，综合考虑温度控制和定价决策，为企业最大化其收益提供决策支持。

1 模型及其最优解

1．1 参数及其意义

笔者选用的参数及其意义如下:I(t)为t时刻的库存水平;p为产品的价格;D(t)为t时刻顾客的需求速率;h为单位产品的库存成本;tf为产品的生命周期(假设在tf时刻产品全部卖完);q(t)为t时刻产品的质量;q0为产品的初始质量;qmin为产品的最低质量(如果产品质量低于该值，那么必须废弃);k为质量衰减系数;θ(t)为t时刻库存的衰减率系数。

1．2 质量衰减模型

在一般情况下，可根据LABUZA提出的方法，将产品质量衰减动态表示为:

式中:k为产品的质量衰减系数;指数n为反应阶数，一般取0，1两个值。笔者在其取1的情况下进行考虑，并求解微分方程式(1)，可得:

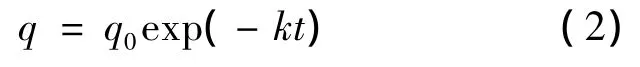
而质量衰减系数k由Arrhenius方程决定:

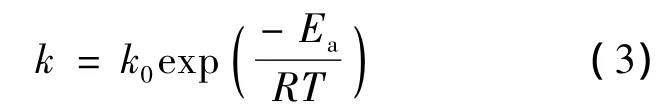
式中:k0为与反应速率有关的一个常数;Ea为控制质量衰减的活化能;R为气体常量;T为绝对温度。

基于文献［19］中介绍的关于能量消耗的模型，可以把温控成本函数表示为:

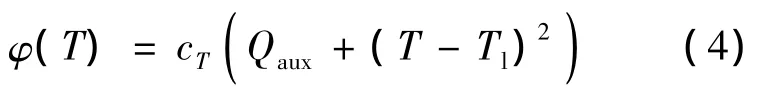
式中:Qaux为能量消耗的常值;Tl为自然温度;cT为成本系数。

由于产品最小质量qmin在tf时取得，由式(2)可知:qmin=q0exp(－ktf)，即:

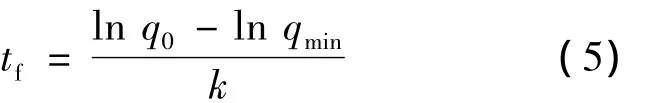
将式(3)中k值代入式(5)，可得:

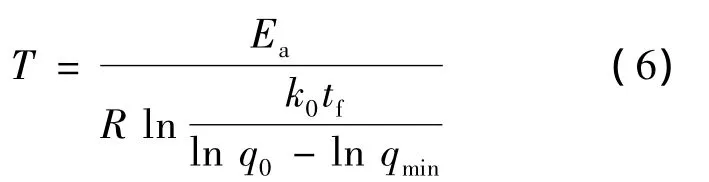
将式(6)代入式(4)中可把温控成本函数改写为:

1．3 温度控制下的定价模型

根据文献［20］以及YAO等的研究成果，假设需求函数D(p)是p的线性减函数，即D(p)=α－βp，其中α为市场容量，β为价格敏感系数，市场价格p需满足约束0≤p≤α/β以保证需求非负。系统初始库存水平为I0，在不考虑生产和补货的情况下，库存的消耗由顾客的需求和产品自身的衰减造成，即:

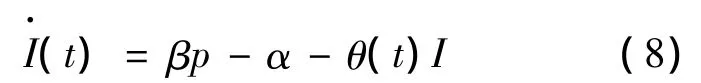
式中，θ(t)为库存的衰减率系数。

企业利润由销量毛利润减去库存成本和温控成本组成，可由式(9)表示:

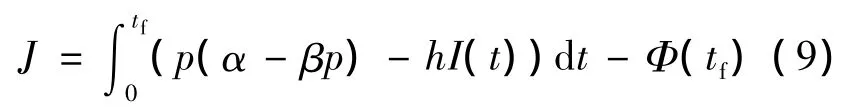
因此，可建立最大化企业利润的优化模型为:

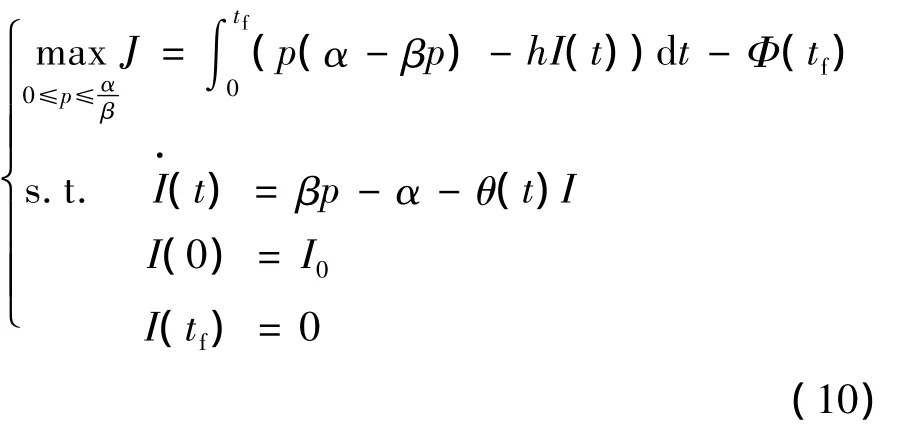
结合库存水平的初始条件I(0)=I0及终端条件I(tf)=0，求解系统状态方程式(8)，所得到的库存水平和产品价格分别为:

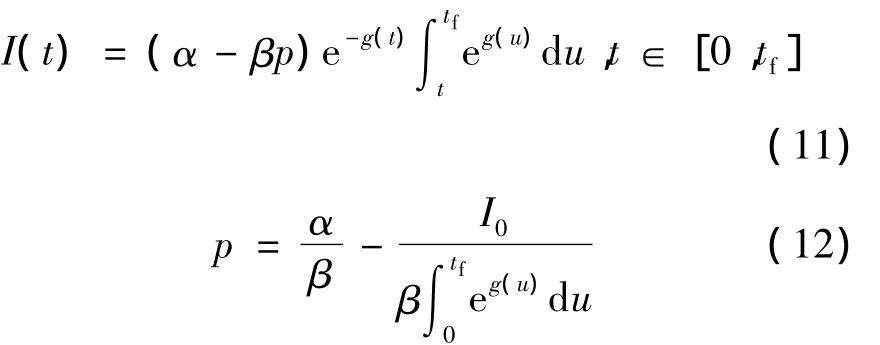
易验证 p∈［0，α/β］，事实上，根据式(11)，可得:

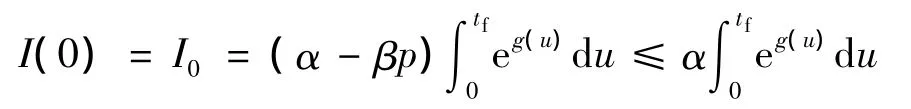
进一步有:

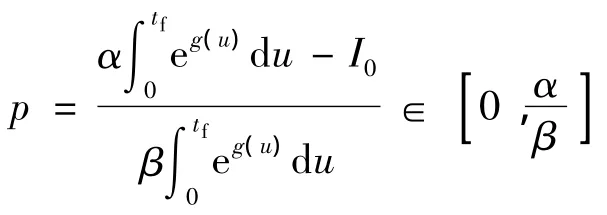
将式(7)，式(11)和式(12)代入目标函数式(9)中，可得企业总利润为:

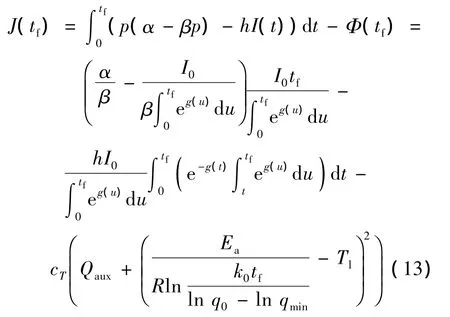
由式(13)可知，利润函数J(tf)是一个关于生命周期tf的非线性函数。通过一维搜索算法可找到最大化企业总利润生命周期t*f，进而由式(6)求得最优控制温度T*，由式(12)可得最优价格p*。

2 数值算例

笔者以需要冷冻保存的易逝性食品为例计算最优控制温度及产品价格。根据HONG等及HUA等［20］的研究，各参数取值如下:α =18，β=0．9，h=0．2，I0=400，cT=1．18 × 10－3，Qaux=20，Ea=85 610，R=8．314 4，k0=1．14 ×1015，q0=1，qmin=0．6，Tl=293。一般来说，随着保质期限的临近，易逝性食品变质腐烂的速度会加快，其衰减率系数可表示为时间的凸增函数，笔者假设θ(t)=θt2，其中 θ=0．001。

由式(13)，在上述参数下通过对tf进行一维搜索，可找到使总利润最大的生命周期19．37，进而分别由式(12)和式(6)求得最优售价p*=10．59，最优控制温度 T*=268．81，此时总利润J*=903．65。利润J随生命周期tf的变化曲线如图1所示。

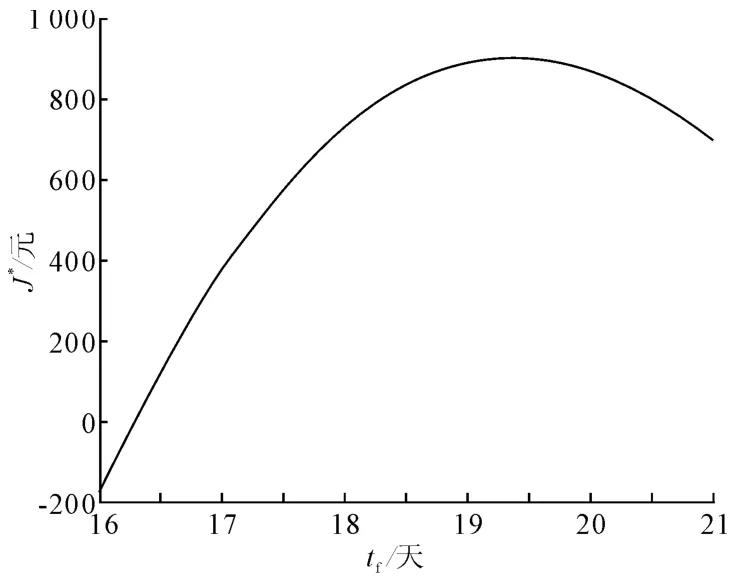
图1 利润随tf的变化曲线图

为了更好地分析各参数变化对最优值的影响，笔者在考虑其他参数不变的情况下，分别改变β，θ，I0和h的取值，得到最优策略及相应利润如表1～表4所示。

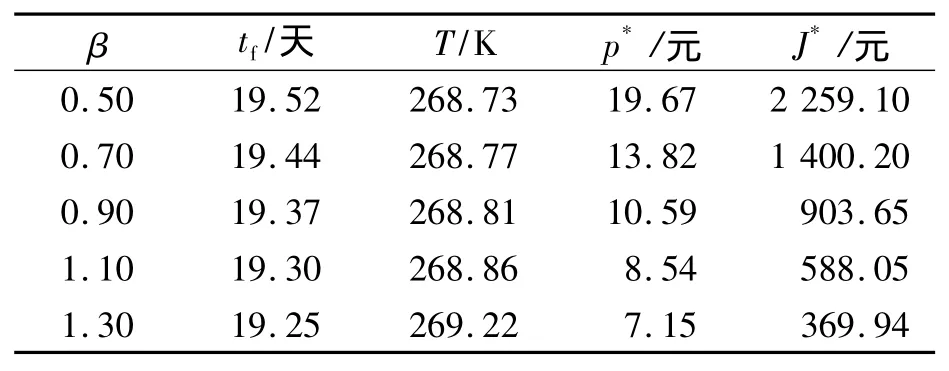
表1 β变化对各最优值的影响

从表1可以看出，最大利润J*和最优价格p*受价格弹性系数β影响较为明显。一般来说，β越大，顾客选择商品时越容易受商品价格影响，因此企业通常采用降低价格的手段来刺激需求，加快库存的消耗速度，这使得产品的销售周期缩短，从而相应的温度控制成本也会降低。特别地，注意到随着β的增大，最优利润会大幅减少。

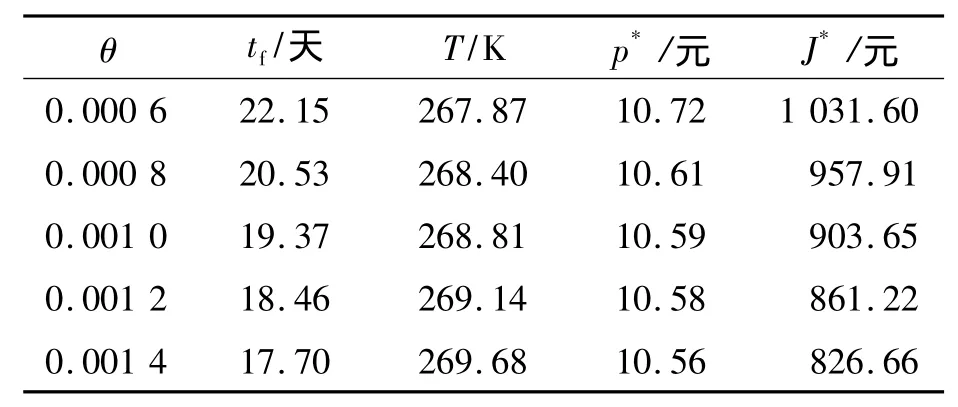
表2 θ变化对各最优值的影响

从表2可以看出，产品衰减率系数越大，其生命周期(销售周期)越短，也就意味着产品更不易保存。从系统方程式(8)中可以看出θ越大，库存衰减得越快，根据tf的定义，其生命周期越短。在这种情况下，企业一般会适当压低价格来使产品尽快出售，减少损失，这便导致了利润的下滑。

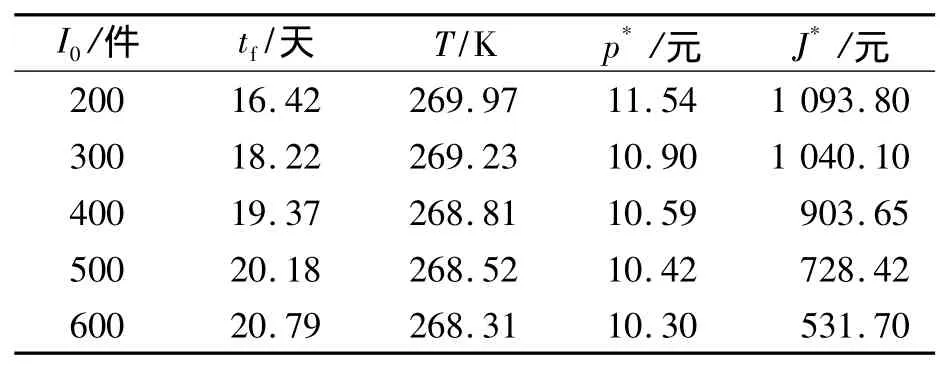
表3 I0变化对各最优值的影响

表3体现了各目标值随初始库存I0的变化情况，可以看出初始库存越大，将产品全部售出的时间就会越长。当面对较大的库存压力和较长的销售周期时，企业往往会采取各种措施使产品尽快出售，例如降低产品的价格。

表4描述了库存成本h对各目标值的影响。随着库存成本的不断增加，企业便会考虑通过尽快消耗库存来减少成本，因此需要降低售价以将产品尽快出售，相应地，产品的销售周期(生命周期)tf也会缩短。

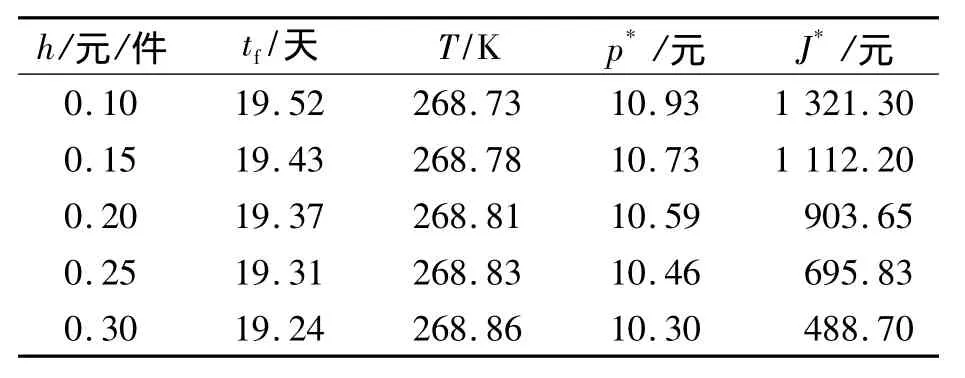
表4 h变化对各最优值的影响

3 结论

笔者充分考虑了销售价格和温度控制对易逝性食品收益的影响，将温度视为连续变量，建立了最大化企业利润的定价模型。最后利用数值算例对所求结果进行了检验，并分析了相应的管理意义。所得结论为企业制定产品价格与存储温度的决策提供了参考依据。

［1］ BLACKBURN J，SCUDDER G．Supply chain strategies for perishable products:the case of fresh produce［J］．Production and Operations Management，2009，18(2):129－137．

［2］ KIM S W，BELL P C．Optimal pricing and production decisions in the presence of symmetrical and asymmetrical substitution［J］．Omega，2011，39(5):528 －538．

［3］ 殷明，郑士源，丁以中，等．基于期权理论的国际海上集装箱运输协议动态定价决策［J］．系统工程理论与实践，2012，32(10):2297－2305．

［4］ 魏昕，朱益民，胡奇英．垄断厂商相依多产品的定价［J］．运筹与管理，2012，21(5):145 －153．

［5］ 何黄吉．企业产品最优定价决策模型的研究［J］．武汉理工大学学报:信息与管理工程版，2006，28(2):128－130．

［6］ 陶文源．基于供应链伙伴关系的产品定价问题研究［J］．武汉理工大学学报:信息与管理工程版，2003，25(1):107－110．

［7］ YAO Z，LEUNG S C H，LAI K K．Analysis of the impact of price－sensitivity factors on the returns policy in coordinating supply chain［J］．European Journal of Operational Research，2008，187(1):275 －282．

［8］ SCHÜTZE J．Pricing strategies for perishable products:the case of Vienna and the hotel reservation system hrs．com［J］．Central European Journal of Operations Research，2008，16(1):43 －66．

［9］ LABUZA T P．Application of chemical kinetics to deterioration of foods［J］．Journal of Chemical Education，1984，61(4):348 －358．

［10］ RONG A，AKKERMAN R，GRUNOW M．An optimization approach for managing fresh food quality throughout the supply chain［J］．International Journal of Production Economics，2011，131(1):421 －429．

［11］ WANG X，LI D．A dynamic product quality evaluation based pricing model for perishable food supply chains［J］．Omega，2012，40(6):906 －917．

［12］ 邵宝玉，石岿然．再制造过程中再制造品的质量选择及其影响［J］．工业工程，2012，15(3):83 －86．

［13］ 陈休晔，刘晓，邵鲁生．基于突发事件的易腐产品分销计划问题［J］．上海交通大学学报，2011，45(12):1800－1806．

［14］ HONG H，LUO Y，ZHU S，et al．Application of the general stability index method to predict quality deterioration in bighead carp(Aristichthys nobilis)heads during storage at different temperatures［J］．Journal of Food Engineering，2012，113(4):554 －558．

［15］ KUO J C，CHEN M C．Developing an advanced multi－temperature joint distribution system for the food cold chain［J］．Food Control，2010，21(4):559 － 566．

［16］ AKKERMAN R，FARAHANI P，GRUNOW M．Quality，safety and sustainability in food distribution:a review of quantitative operations management approaches and challenges［J］．OR Spectrum，2010，32(4):863－904．

［17］ CORZO O，BRACHO N，MARJAL J．Color change kinetics of sardine sheets during vacuum pulse osmotic dehydration［J］．Journal of Food Engineering，2006，75(1):21 －26．

［18］ TSIRONI T，DERMESONLOUOGLOU E，GIANNAKOUROU M，et al．Shelf life modelling of frozen shrimp at variable temperature conditions［J］．LWT － Food Science and Technology，2009，42(2):664 －671．

［19］ DORATO P．Optimal temperature control of solar energy systems［J］．Solar Energy，1983，30(2):147 －153．

［20］ HUA Z，LI S．Impacts of demand uncertainty on retailer＇s dominance and manufacturer－ retailer supply chain cooperation［J］．Omega，2008，36(5):697－714．