高速运动转子动静压轴承油膜动力稳定性分析

张大为，王佳亮

(哈尔滨电机厂有限责任公司，黑龙江 哈尔滨 150040)

0 引言

动静压轴承为兼有动压、静压轴承两者优点的轴承，其在正常转速时动压工作，低速旋转时静压工作的油膜轴承。轴承启动、制动过程中或主轴转速低于某一临界值时为静压作用，在轴承正常运行过程中动压租用，静压供油系统停止工作。这样工作的动静压轴承称为静压浮升式动静压轴承，经常用于大型汽轮发电机转子动平衡试验，转子转速最高约4300 r/min。

现对于发电设备转子分析动静压轴承油膜的动态性，即动静压轴承在高速工作情况下的动力学性能，如极限转速、不稳定性和对不平衡量的响应。在转子轴在升速运动过程中，轴的中心位移变化幅值迅速增加，以致难以控制，这对于轴承－轴系统则是一个极危险现象，可造成转子轴及轴承部位严重烧毁，继而造成价值几千万设备的损失。

1 动静压轴承工作原理

如图1两套供油系统，低压油PL将通过动压油腔进入轴承，而高压油PS进入静压油腔。注入静压油腔的油从轴承间隙泻出而形成一层压力油膜。若静压油腔与静压油腔有效面积的乘积等于外载荷，轴被顶起，脱离与轴承的直接接触，实现了液体摩擦。当轴以正常工作转速运行时，静压供油系统停止向静压油腔供油，此时另一个系统向动压油腔供油以保持动压润滑的需要，这时的外载荷将全部由油膜的动压效应所产生的作用力承受。

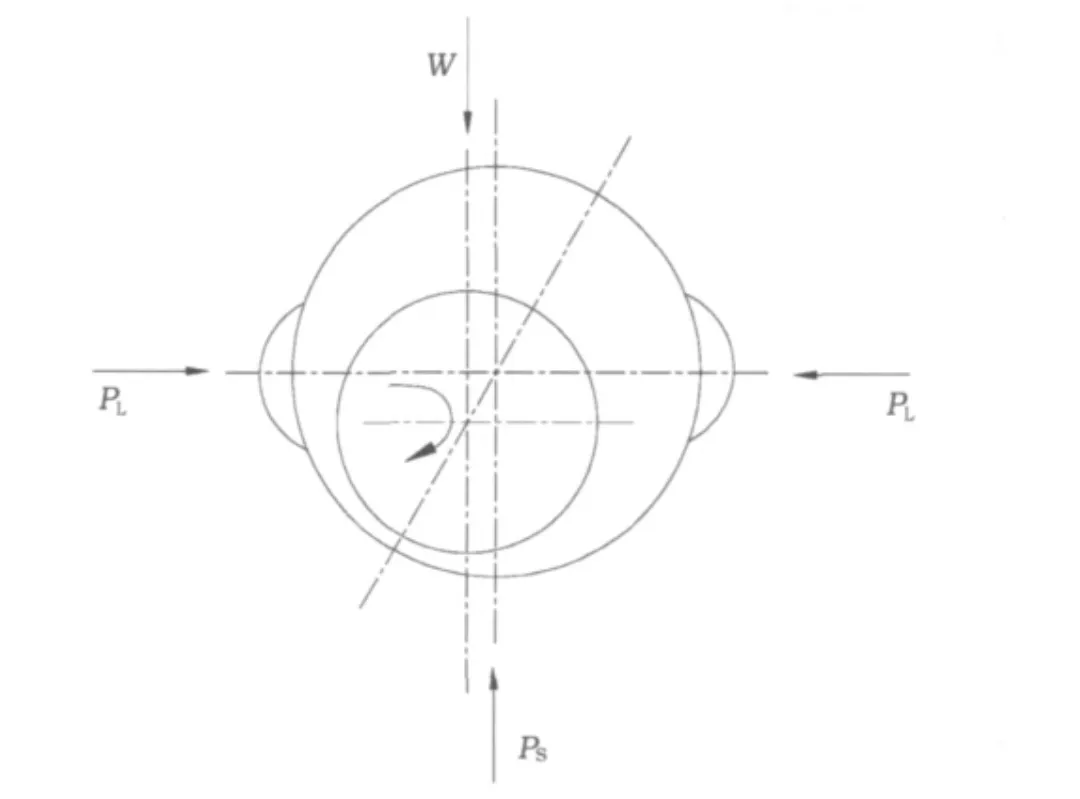
图1 动静压轴承示意图

2 油膜轴承－轴系统失稳现象成因

当一个油膜轴承－轴系统的速度逐渐升高时，可以测得轴的中心位移随时间变化，如图2所示，对于动静压轴承－轴系统，由于油膜产生的各向不同性的缘故，在高速轻载荷时，往往有两个频率。

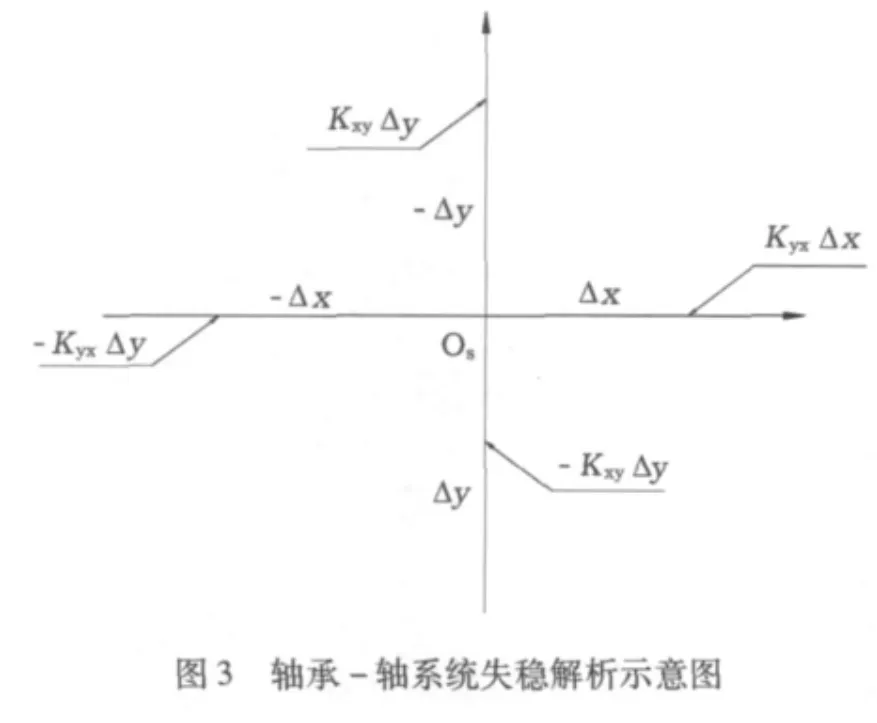
油膜轴承－轴系统失稳现象成因:油膜的动态特性系数中有两个交叉刚度系统，即Kxy、Kyx。这两个刚度系数对油膜轴承－轴系统的失稳有很大的影响。图3所示，图中OS是轴的瞬时平衡位置，若交叉刚度Kxy为负、Kyx为正，则交叉刚度与位移增量乘积所决定的x、y扰动力增加有:

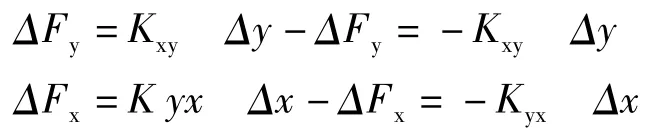
如果轴中心一旦偏离平衡位置，ΔFy、－ ΔFy、ΔFx、－ΔFx正好增加轴中心涡动的能量，造成油膜轴承－轴系统失稳。经分析Kxx、Kyy值大，则刚度高，有利于提高油膜轴承－轴系统的固有频率，这利于增加系统的稳定性。阻尼 Bxx、Byy值大，利于抑制振动，而Bxy、Byx对稳定性影响很小。

3 稳定性分析

以下通过对4个刚度系数和阻尼系数分析来判断油膜轴承－轴系统的稳定性。

轴在油膜中承受的扰动力的运动方程为:

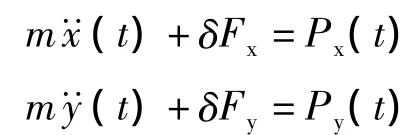
式中:

m——轴的质量;

x(t)、y(t)——轴在x、y方向位移随时间的变化;

Px(t)、Py(t)——作用在轴x、y方向的扰动力;

δFx、δFy—— 分别是轴受力的 x、y 方向的油膜力。

该方程式一元四次多项式。解方程应有4个根，即两对共轭复数根:

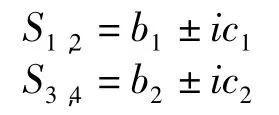
由特征方程根的性质可以判别油膜轴承－轴系统的稳定性。系统稳定的充分必要条件Re(s1)＜0(i=1，2，3，4)。在这里即根的实部为负，b1＜0，b2＜0。假设 S1，S2，S3，S4是特征方程 c(s)的4 个根。用待定系数法，待定系数为H，I，J，K。则变为下式:

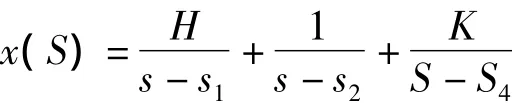
为求得轴受扰动力作用后轴心位移随时间变化方程，对上式进行反拉氏变换。反拉式变换为L－1[]，有:

式中给出在油膜中运动的轴受扰动力之后的曲线方程。

4 结语

对于x(t)=Hes1t+Ies2t+Jes3t+Kes4t方程分析可知，只有四个根的实部均小于0时，x(t)的振幅才能随时间衰减，上式能收敛，即系统受扰动力作用后能重新稳定下来，说明这个系统就是稳定系统。只要其中一个根实部大于0，则上式不能收敛。x(t)的振幅不断增大，是不稳定系统。若根的实部等于0，则x(t)不收敛也不发散，是稳定振动。在发电机转子试验过程中，转子轴承需提供一个旋转稳定的支持系统，在设计轴承系统时要充分考虑轴承系统各部位振动幅度是否影响试验的结论，笔者着重研究了动静压轴承油膜动力稳定性，以便在高速旋转过程中将轴承油膜对转子不稳定性的因素排除，将转子自身的不稳定因素显露，将有利于转子整体性能提高。