看图学数理

曼尼斯·凯洛许

1、2、3、4、5……我们常用这些数字来数数。数的用途很多，比如用来做游戏。很多人发现：用不同的方法把数加在一起，可以创造出很多有趣的图案。

你用数字能创造出哪些有趣的图案呢？

表示数的方法很多。可以在纸上画

在桌上放6张邮票，把它们排成一对一对的，最后一个也没有剩。

把所有东西通通配成对，一个也没剩，我们就说它是偶数。所以6就是偶数。

有时候，老师会要求班上的同学两个两个排一排。如果每个同学都能找到伴，配成对，那么班上的人数就是偶数。如果其他人都配成对后，还剩一个同学没找到伴，配不成对，那么班上的人数就是奇数。

在桌上放5个苹果，试着把它们两两配对。因为有一个配不成对，所以5是奇数。

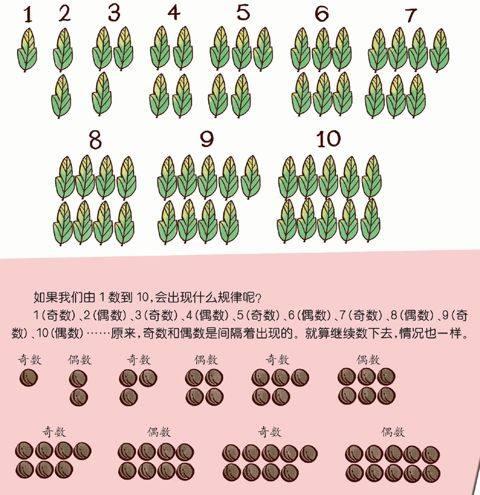
如果从1按顺序写到10，就叫“连续整数”。这些数当中，哪些是偶数呢？是不是2、4、6、8、10？有没有看到下图中这五个数下面的树叶，都能两两配对？如果这五个数按由小到大或由大到小的顺序写下来，就叫做“连续偶数”。

同样地，1、3、5、7、9这五个数下面的树叶不能完全两两配对，最后都剩一片，这五个数就是奇数，按顺序写下来，就是“连续奇数”。

如果我们由1数到10，会出现什么规律呢？

1（奇数）、2（偶数）、3（奇数）、4（偶数）、5（奇数）、6（偶数）、7（奇数）、8（偶数）、9（奇数）、10（偶数）……原来，奇数和偶数是间隔着出现的。就算继续数下去，情况也一样。

那17是奇数还是偶数呢？你可以拿17个小球出来做实验。把它们两两配对，看最后有没有剩下一个。也可以在嘴里依次念“奇数—偶数—奇数……”的口诀，念一声，就拿走一个小球，一直念到17，来检验刚才的答案对不对。

如果用不同的方法把这些数字相加，会得到什么数呢？

两个偶数相加，会得奇数还是偶数呢？让我们用下面的图片加加看。

你不用算就知道，这些小车刚好两两配对，一个也不剩，所以结果是一个偶数。把两个偶数加在一起，结果还是一个偶数。你发现了吗？

偶数+偶数=偶数

按照数量，在桌上摆两组珠子，然后把上图右边那组左右颠倒，变成下图中的样子。

把两组珠子组合起来，原来每组各多出来的一个珠子，正好重新两两配对，最后可得到左图的结果。

看到了吗？随便把两个奇数两两相加，会得到一个偶数。

奇数+奇数=偶数

知道上面的规律后，不需配对，我们就可知道17是奇数：17=7+10=奇数+偶数=奇数。用这样的方法就可方便地得出比10大的数是奇数还是偶数了。例如14=4+10=偶数+偶数=偶数。那么11、12、14、15、16、18、19是什么数呢？

你会发现：

一个两位数，如果个位上的数是奇数，那么这个数就是奇数；如果个位上是偶数，那么它就是偶数。即使十位数字不是1，这个规律也成立。

除了配对以外，还能用其他图案来表示奇数。下面是数字“7”的配对图案。把下图上排的3个扇贝换个方向，与下排的4个扇贝形成一个像书角一样的新图案。

用同样的方法，把连续奇数排成下面的图案。

从1开始的连续奇数相加，结果会是什么呢？1和3相加得4，相加以后的图案是正方形，如右图所示，所以说4是“平方数”。在4的正方形图案中，每边都有2个纽扣。所以，我们说4是2的平方，2的平方是4。

左面的图案虽然是正方形，但它的数目不是平方数。平方数图案的每一排一定有一样多的纽扣。

让我们在1和3相加的基础上再加上下一个奇数5。我们又得到了一个正方形的图案，它是平方数。这个平方数每边都有3个纽扣。所以，9是3的平方，3的平方是9。

用同样的方法加上下一个奇数7看看。是不是又排成一个正方形呢？它是不是平方数？

再想想看，1是不是平方数？它是不是每边都只有一个东西的正方形？因此，1是1的平方，1的平方是1。

从1开始的连续奇数相加，可以排成一个正方形的图案，也就是说，它们加起来是平方数。

例如1+3+5+7=16，我们可以看出，16排成了一个正方形的图案，它是平方数，每边有4个纽扣。所以，16是4的平方，4的平方是16。

你能证明下一个平方数是25吗？以此类推，你又能证明接下来的三个平方数分别是36、49、64吗？如果东西不够摆，可以在纸上画圆圈或黑点来代替。

赶紧动手试试吧！