流体力学中牛顿运动定律的应用

侯承志

【摘 要】结合多年的教育教学实践经验，作者在本文论述了牛顿运动定律在流体力学中的一个具体运用，即用来解释理想液体在水平管中作稳定流动时的压强与流速的关系，该方法比其他方法更简单明了，易于学生接受。

【关键词】牛顿运动定律；流体力学；理想液体；压强；流速

多年的教育教学实践经验告诉我们：教学要看对象，要有针对性，要因材施教。对于我们所在的高职高专院校现在招收的三年制普通专科学生而言，他们都是高中毕业后参加当年普通高招录取过来的，基础知识比较扎实，知识面也比较宽，分析问题和解决问题的能力也都比较强。因此，在学习理论课程时，不但要进行定量的讲授，而且要增强哲理性、逻辑性的讲授与推导，并且要求理论与实际相结合，只有这样才能满足他们的学习要求，同时也才能调动他们学习的积极性。如我们现在所使用的教材《医学物理学》中“液体的流动”一章，在解释理想液体在水平管中作稳定流动时压强与流速的关系时，若用牛顿运动定律解释，对他们来说，既庸俗、繁琐，又显得不新鲜、不严密，因此，教材中先是由功能原理推导出伯努利方程：恒量，然后利用，伯努利方程简化为：恒量，结合理想液体作稳定流动的连续性方程恒量，得出結论：理想液体在水平管中作稳定流动时，截面积大，则流速小、压强大；截面积小，则流速大、压强小。如此解释既直观清晰，又严密得体，学生很容易接受，效果也好。

而对于我们学校招收的五年一贯制的学生，由于他们是初中毕业生，知识基础相对薄弱，知识面较窄，他们理解问题、分析问题的能力也比较差，对教材《物理学》中“液体的流动”一章在解释理想液体在水平管中作稳定流动时压强与流速的关系时，有些教材仍用伯努利方程作定量解释，但教师在讲授、推导过程中由于牵涉的知识点较多，难度也大，有些知识学生没有学过，这样使他们接受比较困难，效果不佳。另外还有些教材是直接给出结论的，这样也容易造成学生学习上的困惑，难以理解和掌握。此时若改用牛顿运动定律作定性解释，倒使学生更容易接受些。

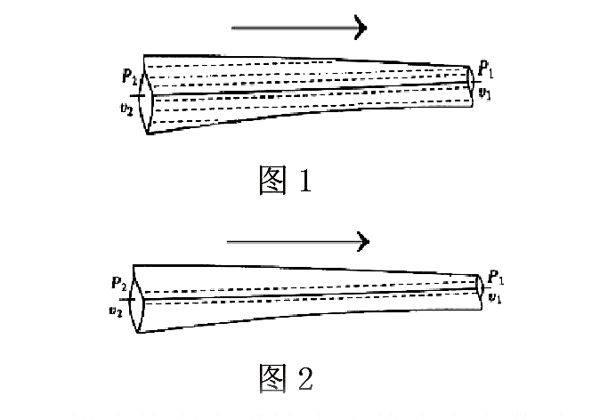
如图1，理想液体在水平管中沿箭头方向作稳定流动，在管子的中心轴线处选取一圆柱形细流管（如图2，所选圆柱形细流管用虚线表示），则该流管内液体是从水平管截面积大的地方流向截面积小的地方。

根据流管内液体作稳定流动的特性，流管内外液体不混淆，即流管内的液体不会流出管外，流管外的液体也不会流入管内，流管内液体始终为恒量。由于液体在流动过程中没有横向混杂，即无横向流速分量，故在垂直于液体流动方向上流管的管壁受管外液体的压力各向相等，也就是说管壁受外围液体的垂直作用力之和为零，对液体在水平方向上的流动情况没有影响。

在平行于液体流动方向上，流管内液体在流动过程中，受到来自前后方液体对流管两个端面的作用力：一方是前端面受到流管前面的液体对它的阻力，力的方向与整个流管中液体流动的方向相反，力的大小等于该处压强与其截面积的乘积，即；另一方是后端面受到流管后面的液体对它的推力，力的方向与流管中液体流动的方向一致，力的大小等于该处压强 与其截面积的乘积，即。于是整个流管中的液体在流动过程中所受的合力为：，即。其中表示圆柱形流管的横截面积，、分别表示流管前后两截面处的压强。

由于流管中液体由截面大的地方向截面小的地方流动时，速度是增大的，所以液体段有一个向前的加速度。设该段液体质量是，由牛顿第二定律得，即，所以。而是流管后端截面积大处的压强，是流管前端截面积小处的压强。于是得到：理想液体在水平管中作稳定流动时，截面积大处的压强大，截面积小处的压强小。再结合连续性方程 可以得出结论：理想液体在水平管中作稳定流动时，截面积大，则流速小、压强大；截面积小，则流速大、压强小。

这样定性地解释理想液体在水平管中作稳定流动时压强与流速的关系，用的知识点较少，很容易使五年制的学生接受。

【参考文献】

[1]潘志达，邱松耀等.医学物理学[M].北京：人民卫生出版社，2006.

[2]申耀德，楼淑英等.物理学[M].北京：人民卫生出版社，2004.

[3]张胜等.物理学[M].西安：第四军医大学出版社，2005.

[4]潘志达等.医学物理学[M].北京：人民卫生出版社，2007.