基于序列的不确定XML整体小枝查询技术

王 鹏，张晓琳

(内蒙古科技大学 信息工程学院，内蒙古 包头014010)

可扩展标记语言XML(eXtensible Markup Language)是标准通用标记语言(SGML)的一种变体，由W3C(World Wide Web Consortium)工作组制定。随着互联网的飞速发展，XML格式的数据在信息世界随处可见，使得XML成为当前数据的通用格式，因此研究利用XML来管理不确定数据具有重要的理论价值和现实意义。

查询处理是数据管理的核心，对于不确定XML查询处理的研究，国内外尚处起步阶段。文献［1］提出的不确定XML查询算法是根据二元结构连接方法中的Tree－Merge－Anc算法［2］改进的，文献［3］提出的不确定XML查询算法是根据整体匹配方法中的TwigStack算法［4］改进的，文献［5］提出的不确定XML查询处理方法是根据整体匹配方法中的TJFast算法［6］改进的，文献［7］提出的不确定XML查询处理方法是根据整体匹配方法中的TwigList算法［8］改进的。基于二元结构连接的方法由于算法本身会产生无用的中间结果而限制查询的效率，基于整体匹配的方法由于算法本身高内聚的特点不方便进行实例树概率值计算和概率阈值过滤。

PrTRIM(Probabilistic TRee Indexing and Matching)算法是将基于序列匹配的LCS－TRIM算法［9］应用到不确定XML的查询。本文以PrTRIM算法作为基础，提出了H－PrTRIM(Holistic Probabilistic TRee Indexing and Matching)算法。H－PrTRIM算法的思想是将PrTRIM算法中子序列匹配和结构过滤过程合并，在子序列匹配同时进行结构过滤，使子序列匹配的结果就是查询的最终结果，避免了子序列匹配过程产生过多不符合模式树结构的中间结果而影响查询的效率。H－PrTRIM算法与PrTRIM算法相比具有如下优势:(1)更适合查询大文档。(2)更适合查询结构复杂的语句。

1 背景知识

1.1 p－文档模型

p－文档模型是一棵包含普通节点和概率分布节点的树。普通节点来自XML文档的元素、属性名、文本值和属性值，概率分布节点用来标识文档中的概率信息。图1为一个PrXML{ind，mux}模型。

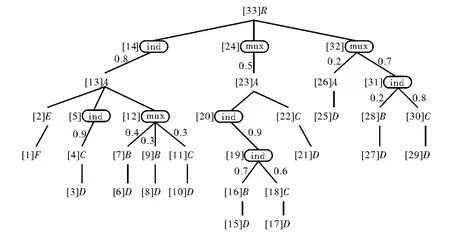
图1 PrXML{ind，mux}模型

1.2 基于序列的Twig模式匹配

可定义Twig模式匹配问题为:给定T wig查询模式Q和一个具有某种索引结构的XML数据库，所谓Twig模式匹配问题就是搜索XML数据库得到所有满足Q模式的XML数据片段，表示为n元组的形式［10］。对于不确定XML，匹配的输入由模式树和概率阈值组成，输出由实例树和实例树的存在概率组成。概率阈值的意义是要求输出的实例树的存在概率要大于等于输入的概率阈值。

序列匹配是一种比较新颖的查询处理方法，它的基本思想是将整个XML文档看作是一个整体，抽取XML文档的内容信息和结构信息，映射到一个序列，建立整体索引。针对模式树，同样抽取内容和结构信息，映射为一个序列。利用模式树的序列来匹配XML文档序列，得到的匹配结果就是查询在XML文档上的查询结果。

基于序列的Twig模式匹配最重要的是匹配结果的等价性问题，有两种情况可能导致匹配结果不等价，分别是假警报(False Alarm)和假不予考虑(False Dismissal)。

设D为XML文档，Q为查询，g为序列化方法。

假警报:g(Q)在g(D)中能找到一个匹配的子序列，但是Q在D中却找不到对应的树片段。

假不予考虑:g(Q)在g(D)中不能找到一个匹配的子序列，但是实际上Q在D中有对应的树片段。

H－PrTRIM算法的序列化方法是PSI(Probabilistic Sequence－based Index)索引和模式树序列化方法，H－PrTRIM算法的序列化方法不含有假不予考虑情况，但含有假警报情况，所以需要利用结构过滤对假警报进行消除。

1.3 PSI索引

如表1所示，PSI索引中每一个元素包括5个子元素。postorder为节点在XML文档中后序遍历的编号，唯一标识一个节点。tag为节点的内容。ppostorder为该节点父节点的postorder。cprob为节点的条件概率。marray记录从XML文档的根节点到该节点经过的类型为mux的概率分布节点，用一个小数表示，概率分布节点mux的postorder为整数部分，概率分布节点mux孩子节点的postorder为小数部分，要求该孩子节点为该节点所在子树的根节点。

图1所示的PrXML{ind，mux}模型对应的不确定XML文档可以生成表1所示的PSI索引。通过PSI索引的postorder和ppostorder能够找到从某一节点到XML文档根节点的路径，进而可以利用PSI索引里cprob计算该节点的存在概率，即在遍历路径的同时将cprob相乘，遍历到根节点时，cprob的乘积就是该节点的存在概率。

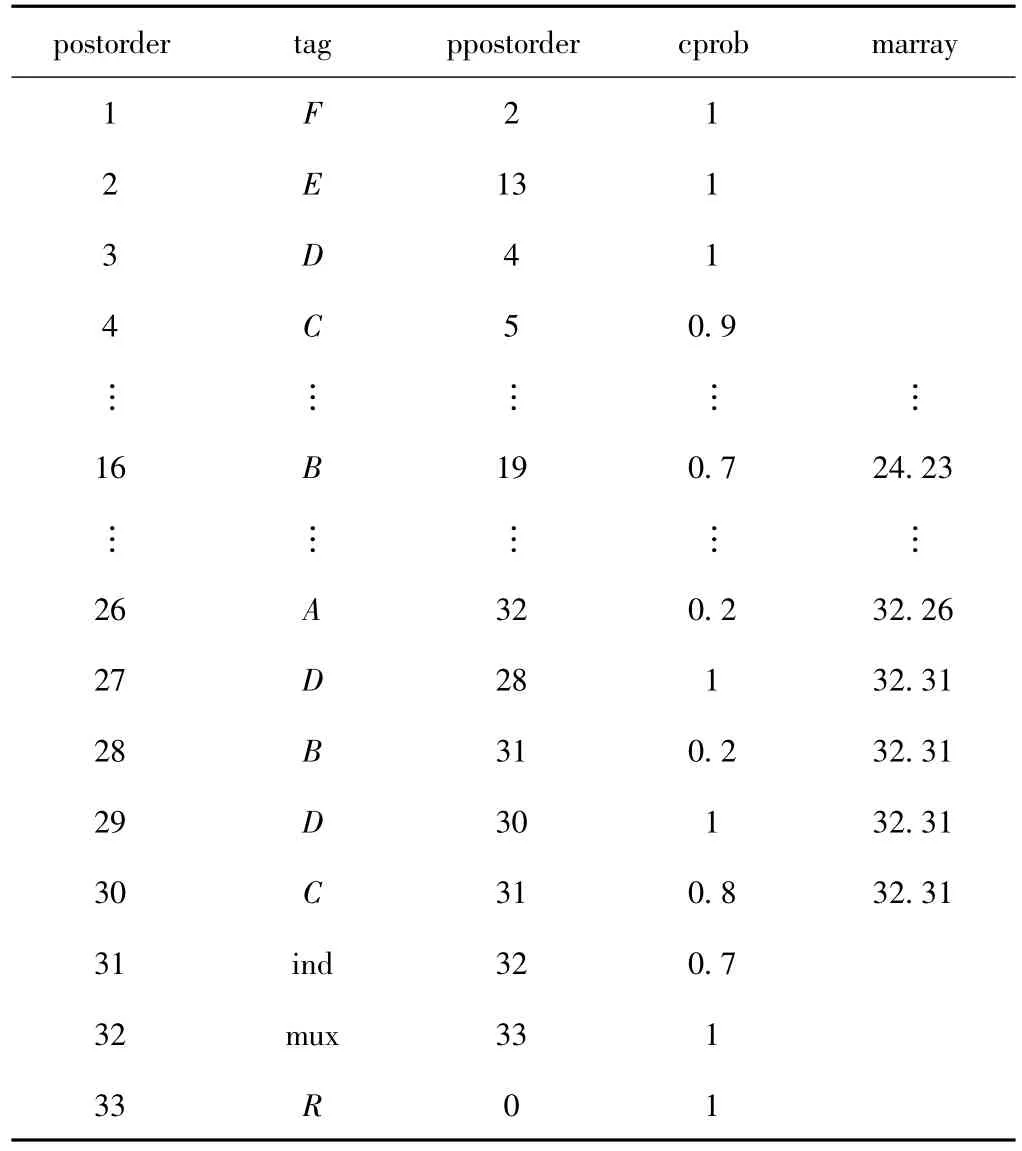
表1 PSI索引部分内容

在实例树中，类型为mux的同一概率分布节点下的不同分支的孩子/后裔不能同时存在，可以借助PSI索引中的marray来判断。以表1中节点26和节点30为例，节点26和节点30的marray分别为32.26和32.31，整数部分相同表示经过同一个类型为mux的概率分布节点32，小数部分不同表示节点26和节点30属于节点32的不同分支，因此节点26和节点30不能同时在实例树中存在。

2 不确定XML整体小枝匹配

H－PrTRIM算法查询之前需要对模式树进行序列化处理，在子序列匹配同时进行结构过滤，在查询的同时进行两次概率阈值过滤。

2.1 模式树序列化

不确定XML的查询语句可以用路径表达式表示，其中“/”表示父子关系，“//”表示祖先后代关系，例如R［A/B］//C。R［A/B］//C可以用树形结构来描述，称为模式树，如图2所示。

图2 模式树

序列化模式树中的每个节点描述为(postorder，tag，ppostorder，R)，其中postorder，tag和ppostorder所代表的意义与PSI索引中元素代表的意义相同。R表示该节点与上下文节点之间的关系，R=“pc”表示该节点与上下文节点的关系为父子关系，R=“ad”表示该节点与上下文节点的关系为祖先后代关系。因此，图2所示的模式树序列化为(1，B，2，pc)，(2，A，4，pc)，(3，C，4，ad)，(4，R，－，－)。

2.2 子序列匹配与结构过滤合并

子序列匹配通过PSI索引中的tag(序列A)和序列化模式树中的tag(序列B)进行，图3所示为一个子序列匹配结果。结构过滤的理论依据是文献［5］中的定义1和定理1。

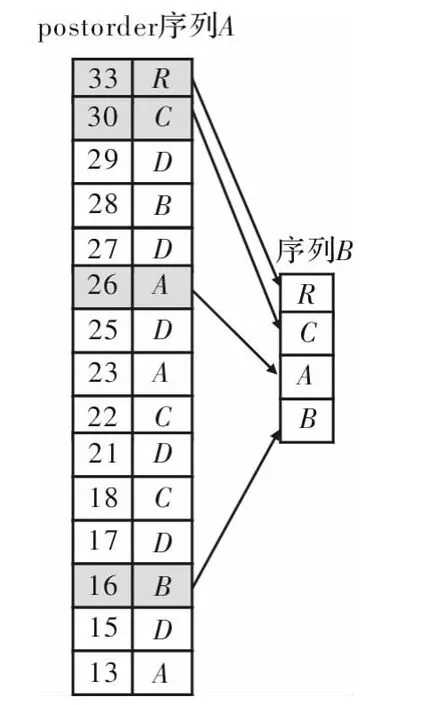
图3 子序列匹配示意

定义1假设两棵树T1和T2对应的序列S1=((A1，B1)…(Am，Bm))，S2=((C1，D1)…(Cm，Dm))，其中Ai和Ci定义了结构，Bi和Di包含了标记。S1和S2称为在位置i处结构一致，当且仅当以下条件满足:(1)1≤i≤m。(2)Bi和Di相等。(3)如果T1中Ai是Bi的父节点，则Ci是Di的父节点，或者S2中Ci的最近祖先在位置Ai处与S1结构一致。

定理1一个查询Q与T结构匹配，当且仅当Q与T在所有的位置k处都保持结构一致，1≤k≤m。

H－PrTRIM算法在子序列匹配的同时进行结构过滤，每当匹配到一个新的节点，就进行结构过滤，根据定义1检查新匹配的节点所在的局部结构是否符合对应模式树的局部结构，如果不符合，则不匹配该节点。根据定理1，子序列匹配得到的结果就是查询的最终结果。例如图3所示的子序列匹配过程中，根据图2所示的模式树结构，匹配过程中节点33，30，26都符合模式树的结构，因此都被接受。当已接受节点33，30，26时，匹配新的节点16，根据模式树的结构节点26与新的节点16应为父子关系，而实际上节点26与节点16并不是父子关系，因此节点16并不会被匹配。以下是在子序列匹配同时进行结构过滤的算法。

2.3 概率阈值过滤

由于组成实例树的每个节点的存在概率是实例树存在概率的子集，即在概率阈值的约束下，只有组成实例树的每个节点的存在概率大于等于概率阈值，实例树的存在概率才能大于等于概率阈值，因此可以在匹配选取节点时进行第一次概率阈值过滤。第一次概率阈值过滤规则:在子序列匹配和结构过滤过程中只选取那些存在概率大于等于概率阈值的节点。

在子序列匹配和结构过滤的同时可以进行第二次概率阈值过滤，一旦发现不符合概率阈值要求的局部结果可以及早地结束，这样可以提高查询的效率。第二次概率阈值过滤规则:在结构过滤过程中每当匹配到一个条件概率不等于1的节点，就将新计算得到的当前概率值与概率阈值进行比较，一旦小于概率阈值，立即终止。

3 实验结果与分析

实验中的算法采用Java语言实现，实验通过HPrTRIM算法与PrTRIM算法对比进行。实验环境为Windows XP平台，主频2.0 GHz，奔腾双核处理器，内存2 GB。实验所采用的数据集是在University Courses数据集中的reed.xml结构基础上随机加入概率分布节点以及概率值人工合成的不确定数据集。

实验用到的查询用例如表2所示。实验针对两个算法分别从3个方面进行:(1)概率阈值对算法响应时间的影响:相同的查询语句(Q3)，相同大小的数据集(58 MB)，不同的概率阈值(0.5～0.9)。(2)算法性能对比:不同的查询语句(Q1～Q5)，相同大小的数据集(58 MB)，相同的概率阈值(0.5)。(3)数据集大小对算法响应时间的影响:相同的查询语句(Q3)，不同大小的数据集(18～58 MB)，相同的概率阈值(0.5)。实验重复进行10次，对数据进行去掉极大值、极小值，然后取平均值的处理。

表2 实验用到的查询用例

概率阈值对算法响应时间的影响如图4所示，概率阈值越小，经过第一次概率阈值过滤后参与查询的节点就越多，所以H－PrTRIM算法与PrTRIM算法的响应时间相差就越大。随着概率阈值的增大，经过第一次概率阈值过滤后参与查询的节点减少，HPrTRIM算法与PrTRIM算法的响应时间逐渐接近。算法性能对比如图5所示，H－PrTRIM算法的响应时间总体上小于PrTRIM算法的响应时间，查询语句Q4最为明显，这是因为查询语句Q4与其他查询语句相比结构更复杂，复杂的结构更能发挥H－PrTRIM算法将子序列匹配和结构过滤合并的优势。文档大小对算法响应时间的影响如图6所示，随着文档增大，H－PrTRIM算法与PrTRIM算法响应时间的差距明显加大，这是因为文档越大，参与查询的节点越多。综上，HPrTRIM算法在应用于查询大文档和结构复杂的查询语句时更能体现出优势。

图4 概率阈值对算法响应时间的影响

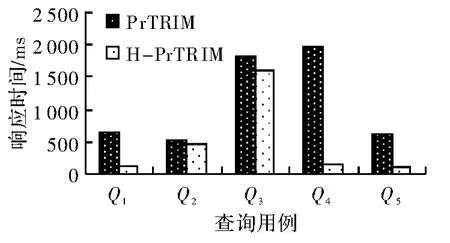
图5 算法性能对比

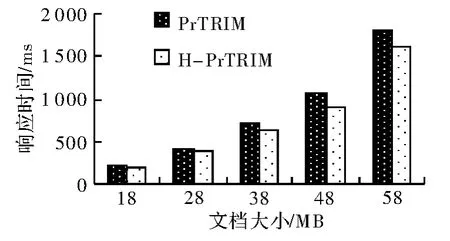
图6 文档大小对算法响应时间的影响

4 结束语

本文在PrTRIM算法的基础上对其进行改进，将PrTRIM算法中的子序列匹配和结构过滤过程合并，在子序列匹配的同时进行结构过滤，使子序列匹配得到的结果就是查询的最终结果。理论和实验表明尽管H－PrTRIM算法与PrTRIM算法相比少一次概率阈值过滤，但H－PrTRIM算法效率仍然高于PrTRIM算法。H－PrTRIM算法与PrTRIM算法相比更适合应用于大文档和结构复杂的查询。

［1］YUN J H，CHUNG C W.Efficient probabilistic XML query processing using an extended labeling scheme and a lightweight index［J］.Information Processing＆Management，2012，48(6):1181－1202.

［2］AL－KHALIFA S，JAGADISH H V，KOUDAS N，et al.Structural joins:A primitive for efficient XML query pattern matching［C］.San Jose，California，USA:ICDE，2002.

［3］ 李亚文.概率XML文档中Holistic Twig查询处理算法的研究与实现［D］.沈阳:东北大学，2009.

［4］BRUNO N，KOUDAS N，SRIVASTAVA D.Holistic twig joins:Optimal XML pattern matching［C］.Madison，Wisconsin，USA:SIGMOD Conference，2002.

［5］ 刘潘.概率XML文档中Twig查询处理算法的研究与实现［D］.沈阳:东北大学，2010.

［6］LU J，LING T W，CHAN C Y，et al.From region encoding to extended dewey:on efficient processing of XML twig pattern matching［C］.Trondheim，Norway:VLDB，2005.

［7］ 张晓琳，吕 庆，刘立新，等.一种高效的连续不确定XML小枝模式匹配算法［J］.计算机应用研究，2013，30(2):364－366.

［8］QIN L，YU J X，DING B.TwigList:make twig pattern matching fast［C］.Seoul，Korea:VLDB，2006.

［9］TATIKONDA S，PARTHASARATHY S，GOYDER M.LCSTRIM:dynamic programming meets XML indexing and querying［C］.Vienna，Austria:VLDB，2007.

［10］ 孔令波，唐世渭，杨冬青，等.XML数据的查询技术［J］.软件学报，2007，18(6):1400－1418.