DV－Hop无线网络定位算法研究

胡华鹏，胡方明，周 惇，张 钊

(西安电子科技大学 电子工程学院，陕西 西安710071)

节点定位问题已经成为无线网络传感器的一个重要研究方向。无线网络传感器中，根据定位过程中是否用到节点间的实际距离，把定位机制分为:基于测距的(Range－based)定位和距离无关的(Range－free)定位方法［1］。

Range－based算法需要测量相邻节点间的实际距离，利用已知节点间的距离和坐标定位出未知节点的位置，但此定位方法的成本较高。该测距方法有Radio Signal Strength(RSSI)，Time of Arrival(TOA)，Time Difference of Arrival(TDOA)和Angel of Arrival(AOA)等。Range－free定位算法则仅利用节点间的距离关联来计算未知节点的位置。定位算法比Range－based算法差，但成本大幅降低。典型的定位算法有DVHop算法［2］，Sum－Dist算法，Euclidean算法和基于连通性的定位算法等。

Niculescu等为避免对节点间距离的直接测量而提出了DV－Hop算法。该算法是基于距离矢量计算跳数的算法。该算法的基本思想是，将待定位节点到已知节点之间的距离用网络中节点平均每跳距离和到已知节点间的跳数乘积来标识，再使用三边测量法和最大似然估计法来获得待定位节点的位置信息。

由于无线传感器网络［3］中DV－Hop算法的锚节点与未知节点之间的平均跳距估算的误差较大，容易造成累积误差［4］。由此本文对原有DV－Hop算法进行修改，提出了一种新的节点位置估计算法。

1 DV－Hop算法的定位过程

DV－Hop的定位算法可以分为3个过程［5－7］:

(1)计算未知节点与每个锚节点的最小跳数。锚节点向邻居节点广播自身位置信息的分组，其中包括跳数字段，初始化为0。接收节点记录具有到每个信标节点的最小跳数，忽略来自同一个信标节点的较大跳数的分组。然后将跳数值加1，并转发给邻居节点。通过这个方法，网络中的所有节点能够记录每个锚节点的最小跳数。

(2)计算未知节点与信标节点的实际跳段距离。每个信标节点根据第一个阶段中记录的其他信标节点的位置信息和相距跳数，利用式(1)估算平均每跳的实际距离

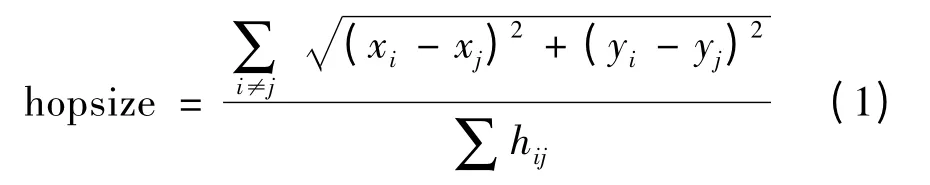
式中，hij为第i个节点到第j个节点间的跳数;(xi，yi)为第i个节点的坐标;(xj，yj)为第j个节点的坐标。假设DV－Hop的模型如图1所示。

图1 DV－Hop算法模型

其中，L1，L2，L3是锚节点;A是一个未知节点;L1，L2，L3这3点之间的距离已知，分别是30，50和80。节点L1～L2的距离为30;跳数为4;节点L1到节点L3的距离为50;跳数为4，根据公式计算节点L1直接每跳的平均距离为［(30+50)/(4+4)］=10。同理亦可得L2的平均每跳距离为［(30+80)/(4+6)］=11，L3的每跳平均距离为［(80+50)/(4+6)］=13。

一个信标节点在计算完与其他各信标节点每跳的平均距离后，在对邻居节点广播的消息发分组中，包含了各锚节点的最新信息。这样，其他节点可以得到锚节点的最新位置信息，一般是周围相邻节点先得到。在网络中，位置信息以广播的方式发射，网络中的节点在收到位置信息时就与原来收到的位置信息进行比较，如果新收到的位置信息比原来的位置信息更新，就抛弃原来的位置信息，将新收到的位置信息储存起来，这样就可以保证节点只储存1条最新的位置信息。未知节点接收到锚节点的每段平均距离，再根据式(2)可计算得到未知节点到锚节点的距离

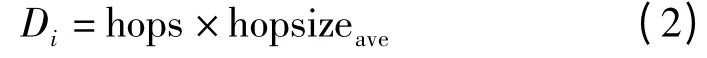
其中，hops为未知节点到锚节点之间的最小跳数。

(3)完成待定节点的位置估计。利用已经得到的数据用三边测量法和极大似然估计法完成位置节点的定位。

DV－Hop定位算法将平均每段的跳距与跳数的距离作为距离的估算值，所以平均跳距在较大程度上决定了DV－Hop的定位精度。若要误差在合理的估算范围内，则要求无线网络中节点分布虚密集、均匀。但网络中的节点较少且分布离散时，就容易造成累积误差。随着跳数的增加，误差将越来越大。

2 DV－Hop算法的改进

2.1 均匀量化模型

对任意节点i，假设信号的最大接收功率为Pmax，最小接收功率为Pmin，对通讯半径进行量化，量化的最大等级为M。任意邻居节点为j，设节点j接收到节点i的功率为Pij，则通过量化得到的距离信息dij为

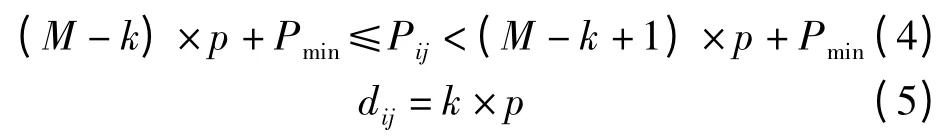
这里k为1～M之间的任意整数，p代表最小量化单位，当M确定后，p是一常数经过上面量化，Pij大的节点所对应的dij值小，说明信号强度越大，节点距离越小，这与实际情况相符。量化后，将节点i的邻居节点集C划分成M个聚类，每个聚类里的节点到i的距离量化值相同。其中p由节点的最大发射功率和最小能识别的功率确定。

在RSSI测距中，距离越近RSSI精度越高，距离越远时由RSSI值得到的误差则较大，因此在量化同时可以采取非均匀量化，对较近的距离采用较小的量化区间，对较远的距离则采用较大的量化区间。

考虑到算法的复杂性，文中运用均匀量化模型，量化后的模型中传统意义上的1跳由多个量化单位取代，其在某种程度上提高了算法的精确性。

其计算步骤为:(1)计算节点与每个锚节点的最小累计量化值。锚节点向邻居节点广播自身位置信息和路径序列。其中自身位置信息包括距离量化值字段，初始化为0，路径序列只包括自身节点编号。接收节点记录具有到每个锚节点的最小累计量化值，忽略来自同一个信标节点的较大累计量化值的分组，同时根据RSSI用式(3)～式(5)来估计其与上一跳节点间的dij，计算出k值，并将结果加入到量化值字段中，通过这一方法，网络中每个节点都能记录到锚节点的最小累计量化单位。(2)计算未知节点和锚节点的实际跳段距离。每个锚节点根据第一阶段中记录的其他信标节点的位置信息和相距量化单位数，利用式(6)估算平均每个量化单位的实际距离

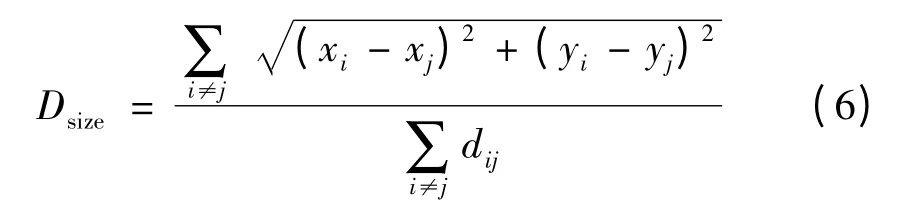
然后，锚节点将计算的平均每个量化单位距离用带有生存期字段的分组广播至网络中，未知节点仅记录接收到的第一个每跳平均距离，并转发给邻居节点。这个策略确保了大多数节点从最近的信标节点接收到平均每个量化值的距离。未知节点接收到平均每个量化值距离后，根据记录的量化单位总数，计算到每个信标节点的跳段距离。

2.2 加权最小二乘法

引入加权最小二乘估计的方法，即根据每个信标节点的位置精度，在最小二乘估计中采用不同的加权系数进行定位计算，以提高定位精度。在一般极大似然估计法的定位过程中，其一般步骤为:已知锚节点1，2，3，4，…，n的坐标分别为(x1，y1)、(x2，y2)、(x3，y3)，…，(xn，yn)，未知节点A的坐标为(x，y)。则根据空间坐标计算

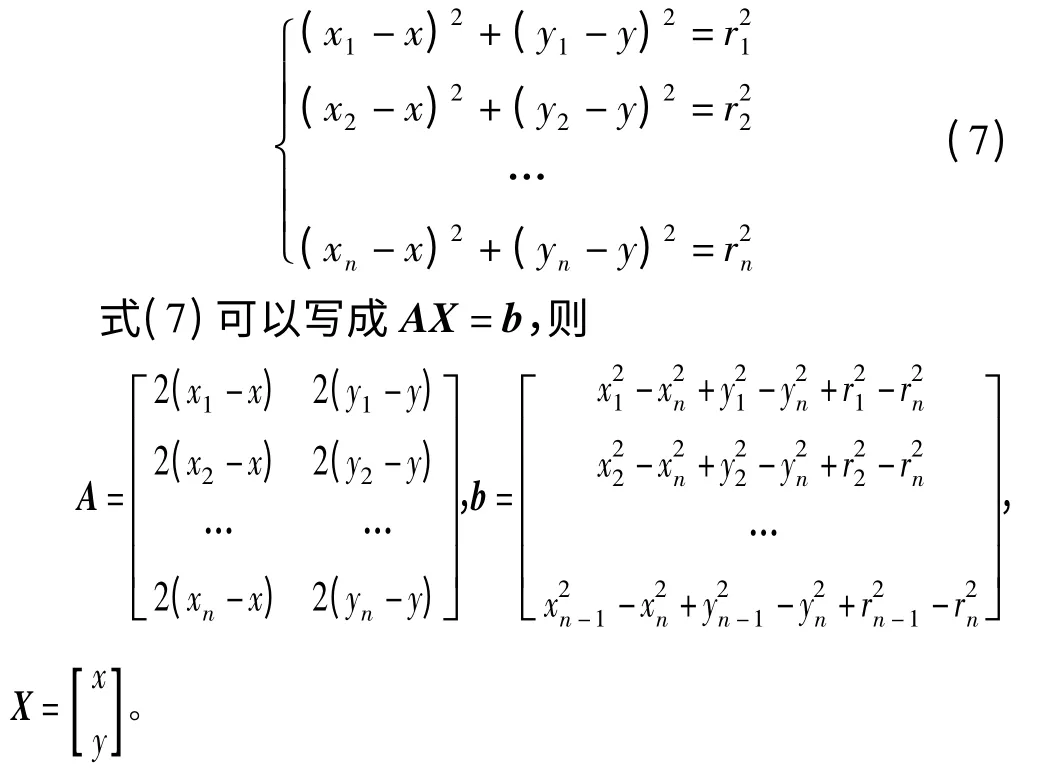
实际应用中，加权系数Wi与误差的协方差有关。理论可以证明，当W取测量值误差方差矩阵的逆矩阵时可使估计误差的方差最小，但实际应用中如何定义加权矩阵W还有待进一步改善。一般情况下，当节点间的跳数越大时造成的误差将越大，所以取的加权值要小一些;而当节点间的跳数较小的造成的误差会变小，所以取的加权值应大一些。

在此引入一个加权系数Wi，利用最小二乘法可得未知节点的坐标为

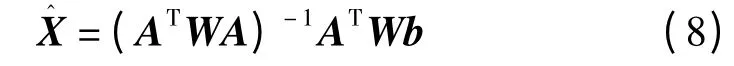
其中，Wi=1/hi，hi为参与定位的锚节点距离未知节点A的最小跳数，则

2.3 仿真与比较

为检验改进算法的性能，在Matlab平台上对传统DV－Hop定位算法和改进算法进行性能仿真对比分析，对算法的性能主要从定位误差方面进行评估。仿真实验网络模型的主要参数如下:网络规模是100个节点，随机分布在100 m×100 m的地域范围内，未知节点的坐标随机产生，节点的通信半径为16 m，量化最大等级为4。每种算法的仿真进行100次，取其定位误差的平均值，其两种算法的定位误差随着参与定位的锚节点个数变化结果如图2所示。

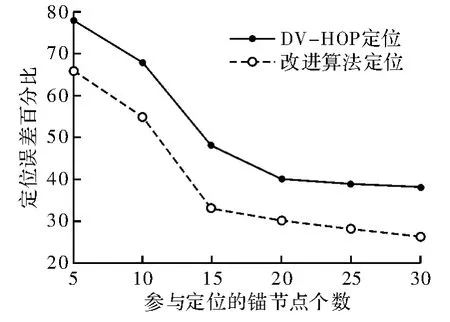
图2 定位误差对比图

由图可知，随着参与定位的锚节点个数的增加，其定位误差越来越小。在锚节点达到20时，其定位误差的下降率趋于平缓。在其对比中，改进算法与DVHop相比，其误差百分比有明显的改善，在锚节点达到30时，其定位误差减少了12%。

3 结束语

针对无线传感器网络定位中的DV－Hop定位算法中定位精度不足，提出了均匀量化模型来提高每段跳距的精度并用最小二乘法来解决定位过程中造成的累积误差。仿真结果证明，该算法在定位精度上有了一定得提高。此处讨论的算法都是停留在仿真试验的基础上，如何在实际系统中实现，并检验算法在现实环境中的性能表现也是一个急需实现解决的问题。

［1］WANG F B，SHI I，REN F Y.Self－localization systems and algorithms for wireless sensor networks［J］.Journal of Software，2005，16(5):857－868.

［2］NIU Y C，ZHANG S D，XU X Y，et a1.An enhanced DVHop localization algorithm for irregularly shaped sensor networks［C］.LNCS 4864，2007:694－704.

［3］SUN L M，LI J Z，CHEN Y，et a1.Wireless sensor networks［M］.Beijing:Tsinghua University Press，2005.

［4］ZHANG S G，CAO J N，CHEN J，et a1.Accurate and energy－efficient range－free localization for mobile sensor networks［J］.IEEE Transactions on Mobile Computing，2010，9(6):897－910.

［5］ 刘文远，王恩爽，陈子军.无线传感器网络中DV－Hop定位算法的改进［J］.小型微型计算机系统，2011，32(6):1071－1074.

［6］ 刘明，包亚萍，刘汉义.无线传感器网络中一种改进的DVHop算法［J］.传感器与仪器仪表，2009，25(4):128－129.

［7］ 王颖，石昊阳.基于DV－Hop的无线传感器网络定位算法［J］.仪表技术与传感器，2012(4):97－99.

［8］ 张新生，赵衍静，李海涛.基于DV－Hop定位算法的改进与研究［J］.计算机科学，2011(2):76－78，90.