基于SAS算法的三维多UAV协同航迹规划方法
王奎民
(中国人民解放军海军 驻锦州地区军事代表室,辽宁 锦州121000)
随着无人飞行器技术逐渐成熟,新型无人飞行器可完成更多的复杂任务,而这些复杂任务是人工驾驶飞机所无法实现的。同时由于无人飞行器造价低、隐身性能好、无人员伤亡等优点,无人飞行器代替人工驾驶飞行器已成为未来发展的趋势,无人飞行器航迹规划作为其关键技术之一已逐渐成为研究热点。
目前无人飞行器航迹规划的研究重点侧重于单个UAV的航迹规划[1],对于多UAV协同航迹规划的研究也多简化在二维环境空间中。具体算法主要有人工势场法、随机路线图法、进化算法和多目标PSO算法[2-5]等。本文针对三维多UAV协同航迹规划问题,提出一种启发式SAS算法进行求解,并仿真验证了算法的正确性与可靠性。
1 多UAV协同航迹规划描述
1.1 SAS算法扩展方式
用SAS算法进行路径规划是从起始点开始扩展直到目标点生成一条路径。在其扩展过程中共有封闭节点、开放节点和当前节点3类扩展点。封闭节点为扩展过程中已经选择的节点,在扩展过程中放入Closed表中;开放节点为扩展过程中已经出现但尚未选择的节点,在扩展过程中放入Open表中;当前节点为扩展过程中正在扩展的节点。
SAS算法扩展方式如图1所示,A为起始点,MB为目标点,扩展的步长为最小航迹段,航迹段数为扩展到当前节点所需扩展的步长个数,已扩展航程为从起始位置到当前节点的真实距离,记为LG,预估到达航程为从当前节点到目标点的直线距离,记为LH。初始航向为从起始点到目标点的连线方向。A点为当前节点,从A点开始扩展得到B,C,D 3个扩展点,将这3点放入Open表中,计算B,C,D各点的代价,假设B点代价最小,将B点从OPEN表中删除,放入Closed表中。将B点作为当前节点,重复以上操作直到目标点。在三维中与在二维中扩展的方式相同。
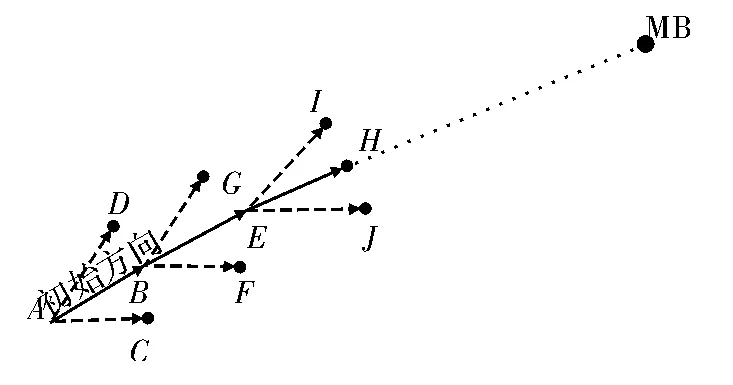
图1 SAS算法扩展方式
1.2 约束函数
多UAV航迹规划存在着单UAV约束和多UAV约束,具体描述如下:
(1)最小航迹段长度。即UAV开始改变飞行姿态前必须保持直飞的最短距离。在SAS算法中扩展一步的步长为最小航迹段长度。
(2)最大拐弯角。其限制了生成的航迹只能在小于或等于预先确定的最大拐弯角范围内转弯。在SAS算法中扩展点与当前节点的直线与当前节点的航向的水平夹角均小于最大拐弯角。
(3)最大爬升/俯冲角。该约束由UAV自身机动性能决定,其限制了生成航迹在高度方向上爬升/俯冲的最大角。在SAS算法中扩展点与当前节点的直线与当前节点的航向垂直夹角小于最大爬升/俯冲角。
(4)最大航迹长度。限制了航迹的长度必须小于或等于一个预先设定的最大距离,在SAS算法中其表达式如下

其中,LH为预估到达航程;LG为以扩展航程;dmax为最大航迹长度。
(5)最低/高飞行高度。其限制了UAV飞行的最低/高飞行高度,在SAS算法中其表达式如下

其中,h为当前节点所在高度;hmin和hmax分别表示最高和最低飞行高度。
(6)最小安全距离。限制了UAV之间必须保持的最小距离,当UAV间小于最小安全距离时认为UAV间发生了碰撞。在SAS算法中其表达式如下

其中,jl为当前节点与其他航迹的距离;danq为最小安全距离。
(7)避开威胁区。限制了UAV在规划过程中必须避开威胁区,由于在SAS算法中,设定的威胁区为火炮球型模型,其表达式如下

其中,d为当前节点到威胁区中心的距离;R为威胁区的半径。
约束(1)~(3)在SAS算法扩展中实现,约束(4)~(7)在SAS算法的评价函数中进行评价。
1.3 评价函数
多航迹规划中每条航迹代价函数为
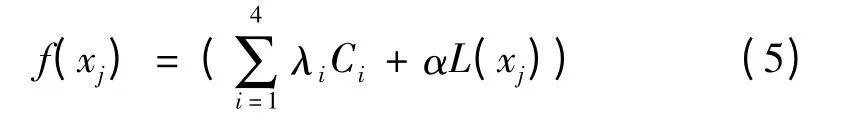
其中,α、λ1~λ4为常值;C1~C4的值根据上文所示计算;L(xj)为协同航程。其计算方式如下文所述。
协同航程为每个UAV规划出的航迹最理想的航程值。在文中协同航程使用二维航迹距离法计算。计算各起始点与目标点之间二维航迹规划后的航迹距离,如图2所示的航迹距离L1、L2、L3、L4。选定航迹距离长的作为参考航迹,协同航程的计算公式如下
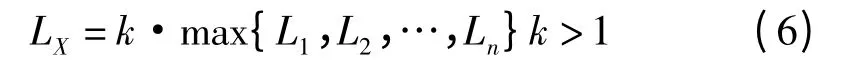
图2 协同航程计算
L(xj)的表达式如下
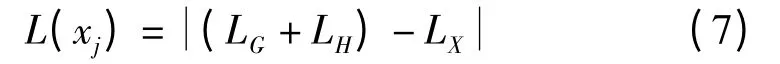
其中,LG为此条航迹已经扩展的航程;LH为此条航迹预估的到达对应攻击目标的航程;LX为协同航程。
2 基于SAS的多UAV协同航迹规划算法
多UAV协同航迹规划的目的是在保证每架UAV最大生存概率的前提下,为每架UAV生成一条航迹,保证UAV同时到达作战区域,以最佳的作战效果完成预期的作战任务。SAS算法的执行步骤描述如下:
(1)将多个起始点放入各自的Closed表中,将起始点作为个自航迹的当前节点,按顺序找到航迹段数最小的作为待扩展当前节点,并对其进行扩展。
(2)将扩展节点放入Open表中,检测当前扩展航迹的当前航迹段是否与其他航迹发生碰撞。
(3)若未发生碰撞,转第(7)步,否则转至第(4)步。
(4)比较当前扩展航迹的当前航迹段标号No.{当前航迹段}和与其发生碰撞航迹的当前航迹段标号No.{碰撞航迹}。
(5)如果No.{当前航迹段}=No.{碰撞航迹},淘汰当前扩展航迹的当前扩展节点。转至第(7)步。
(6)如果No.{当前航迹段}≠No.{碰撞航迹},保存扩展节点,将扩展节点放入Closed表中。
(7)按顺序找到航迹段数最小的作为待扩展当前节点,并对其进行扩展。
(8)如果规划成功则转第(9)步,否则转第(2)步。
(9)输出规划结果。
3 仿真结果分析
仿真环境为根据真实地形生成的200×200像素大小的数字地形图像,如图3所示。设定各无人机均具有相同速度,最小航迹段为10 km,作战半径650 km,最大拐弯角为π/6,最大爬升/俯冲角为π/4,最小安全距离为1 km。作战要求:我方无人机同时到达不同的敌方目标进行打击,无人机不能穿越敌方威胁区,且无人机之间距离必须小于最短安全距离。

图3 数字高程地图俯视图
3.1 3起始点3目标点协同航迹规划
实验中,共有3架无人机,分别从不同的起始点出发飞往不同的目标点,图4显示了3起始点飞往3目标点多航迹规划完成情况。战场中包含4个威胁区,以及山峰等多个禁飞区。具体数据如下:起始点数据如表1,目标点数据如表2,任务分配表如表3。

表1 起始点数据
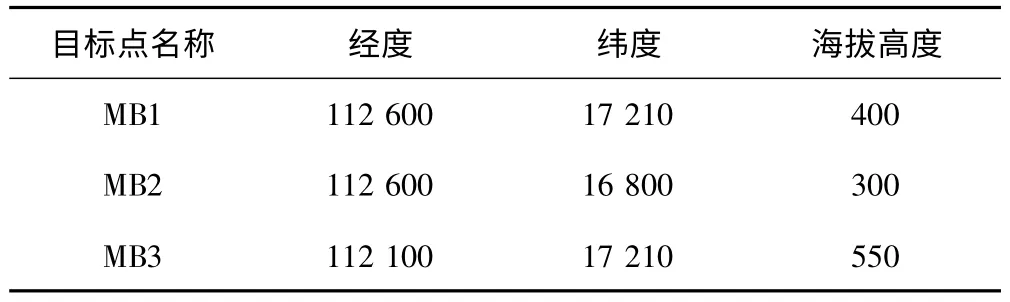
表2 目标点数据
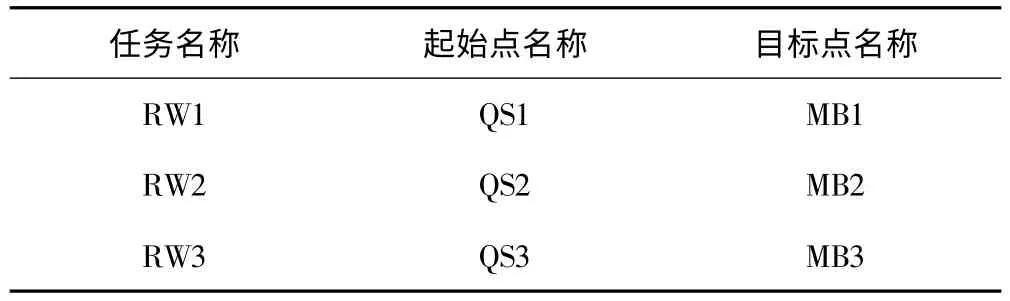
表3 任务分配表
表4给出了本组实验的航迹规划情况,从中可以看到3个任务的航迹距离差值分别为1.1 km、1.3 km、0.25 km,由于无人机飞行速度快,1 km的距离几乎可以忽略不计。从规划速度上讲,3条航迹的规划仅耗时23.7 s。
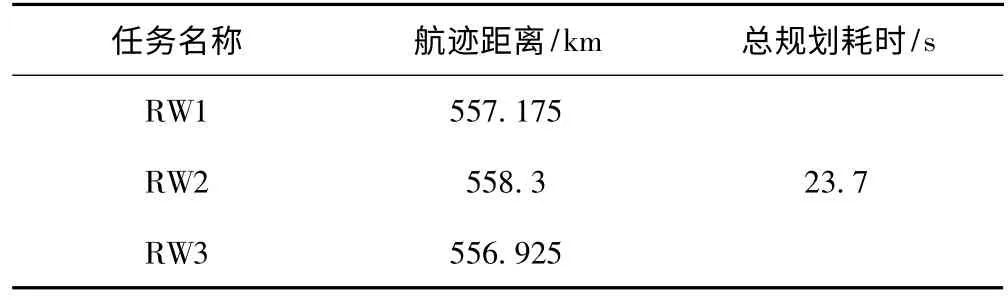
表4 3起始点3目标点协同航迹规划实验结果

图4 3起始点飞往3目标点航迹俯视图
3.2 5起始点5目标点协同航迹规划
本实验的目的是验证航迹规划数目增加时算法的收敛性能。图5显示了5起始点飞往5目标点多航迹规划完成情况。表5给出了本组实验航迹规划情况,从中可以看到5个任务的航迹距离差值在十几到几十之间。5条航迹也仅耗时57.1 s,比三条航迹的规划耗时23.7 s多33.4 s。
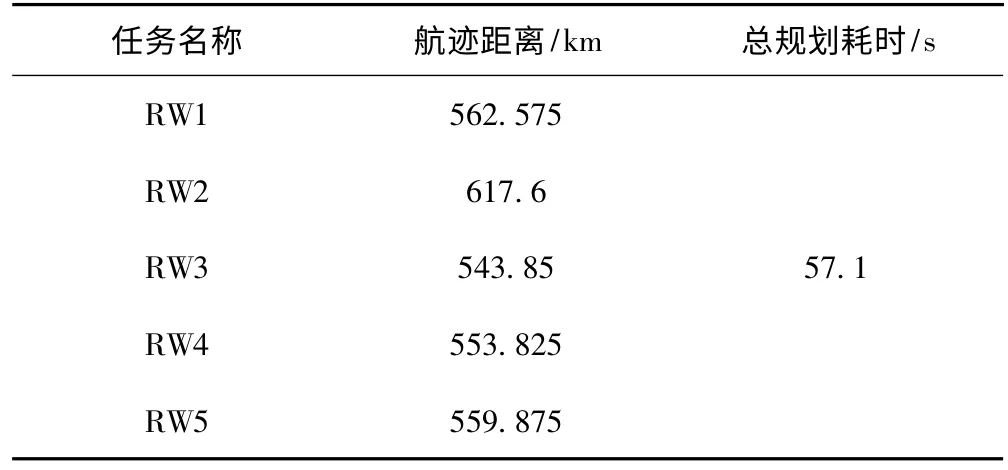
表5 5起始点5目标点协同航迹规划实验结果
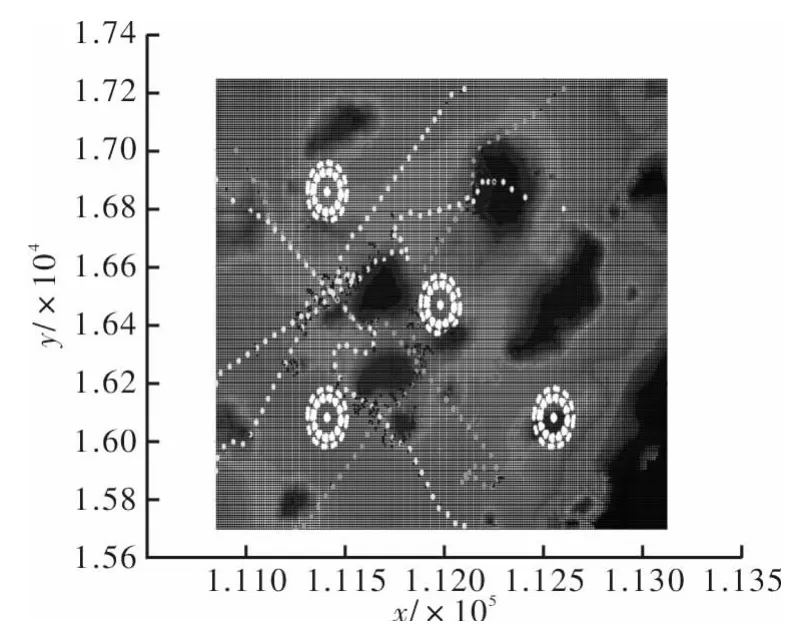
图5 5起始点飞往5目标点航迹俯视图
4 结束语
本文在保证可靠性的基础上使用SAS算法解决了多UAV协同航迹规划问题,仿真结果证明使用SAS算法能够较快地规划出协同航迹,规划出的航迹距离相差较小满足了协同性能的要求。
[1]AKYILDIZ I F,MELODIA T,KAUSHIK R.A survey on wireless multimedia sensor networks[J].Computer Networks,2007,51(4):921-960.
[2]LI C H,LEE C K.Minimum cross entropy thresholding[J].Pattern Recognition,1993,26(4):617-625.
[3]KHATIB O.Real time obstacle avoidance for manipulators and mobile robots[J].International Journal of Robotics Research,1986,5(1):90-99.
[4] 叶文,范洪达,朱爱红.无人飞行器任务规划[M].北京:国防工业出版社,2011.
[5] 朱红果,郑昌文.一种基于PSO的多UAV协同航迹规划方法[J].计算机工程与科学,2010,32(10):142-144.
[6] 丁明跃,郑昌文,周成平,等.无人飞行器航迹规划[M].北京:电子工业出版社,2008.

