一种空间复用MIMO-OFDM联合量化反馈预编码*

周冬跃,胡斌杰

(1.华南理工大学电子与信息学院∥短距离无线探测与通信广东省重点实验室，广东 广州 510640；2.广东工业大学 物理与光电工程学院，广东 广州 510006)

采用正交频分复用 (OFDM) 技术可以提高通信系统信道频谱效率，还可以提高抗频率选择性信道衰落性能[1]，而多输入多输出(MIMO)可以实现空间复用，因而综合两种通信技术的MIMO-OFDM技术可使系统性能得到了更大的提高，被认为未来无线通信中的关键技术之一，现已经成为IEEE 802.11 (WLAN)和 IEEE 802.16 (WiMAX)标准的核心技术。然而，下行链路MIMO-OFDM系统发射端需要进行预编码，特别是在频分双工(FDD)系统中，发射端信道状态信息CSI需要从接收端通过上行链路频道反馈传输，过多反馈比特数不仅降低频带效率，而且增加了CSI延时[2]。采用量化的预编码既可以改善系统通信质量，又减少反馈比特开销。

近年来研究人员对OFDM预编码进行许多有意义的研究，包括发射预处理权矩阵(或矢量)设计、各子载波功率分配和比特分配方面的内容。文献[2-4]提出了基于空间复用OFDM系统的发射权矩阵方案，其中的预编码采用Mt×Ms维(Mt表示发射天线数，Ms表示发射端比特流并行的数量)矩阵，并且其中文献[2]和[4]还尝试了预编码矩阵量化算法，然而这些方案都没有进行功率量化分配优化，因此误码率比较高。文献[5-8]研究了OFDM发射分集方案，利用空间分集方法，采用Mt×1的波束形成向量，提出了分组反馈法算法和引入了旋转角度的插值算法，改善了系统误码特性，但采用空间分集方法虽然误码率较低但发射信道容量也较低，其中文献[7]还提出了一种时域内的量化预处理方法，把预处理环节设计在傅里叶逆变换之后进行，这种方案尽管能在时域实现预处理，但由于OFDM子载波功率分配位于频率域，难以又在频率域内优化子载波功率分配。文献[8]提出的有限比特反馈方法只适用于时分复用(TDD)系统。文献[9-12]提出了OFDM发射端资源分配的算法，分别对预编码矩阵、比特和功率分配提出一些优化方案，但这些优化的理论表达式停留在连续量的阶段，如果把这个连续量反馈到发射端需要的大量比特开销，而对于FDD通信系统而言并不现实。总的来说，现有研究中，对于空间分集研究成果虽然较多，但空间复用预编码矩阵较空间分集系统更复杂，而对预处理权矩阵和功率分配进行联合量化优化也很少。

基于以上情况，文中对空间复用下行链路提出一种量化功率分配和量化分集向量相结合的联合量化预处理方法，建立功率分配码本，并且对文献[11]中子载波功率分配进行修正；同时完善了在分组反馈中预处理矩阵插值表达式，在文献[3]表达式中引入新的旋转角度优化法，使预编码联合优化的结果更精确，从而达到降低系统误码率和提高通信容量的更好效果。

1 预编码工作原理

1.1 系统模型

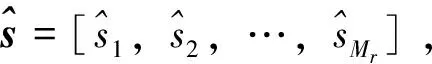
文中的无线信道是频率选择性准静态衰落信道，信道衰落系数在每个OFDM帧间保持不变，而在帧与帧之间随机变化，在频率域输入输出关系就可以用式(1)来表示：

(1)

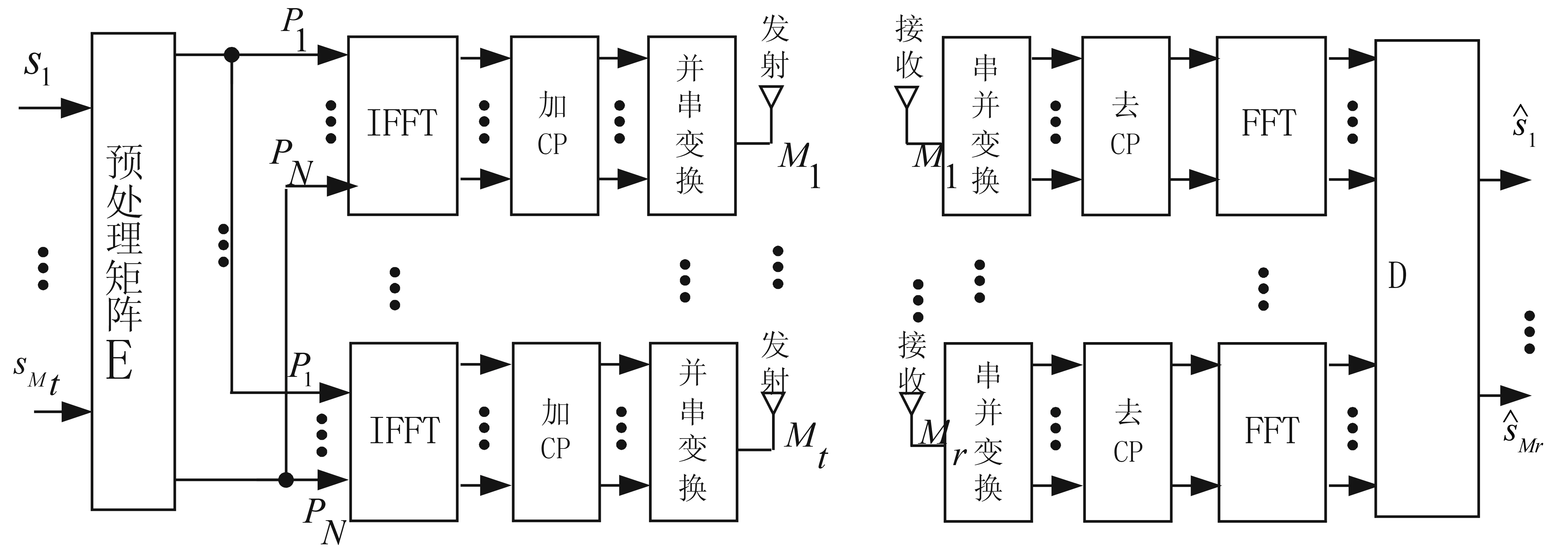
图1 MIMO-OFDM空间复用系统框图Fig.1 Block diagram of MIMO-OFDM spatial multiplexing system

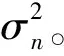
1.2 OFDM预处理技术

1.2.1 理想信道状态信息条件下的预处理矩阵 如果发射端能得到准确信道状态信息H，那么发射端的最佳预处理矩阵E可以通过信道的奇异值分解得到[3]，即对信道矩阵进行奇异值分解：

(U,VH) =svd[H]

(2)

式中：svd[·]表示奇异值分解运算，U、VH分别是信道H奇异值分解的左、右酋矩阵，右酋矩阵就是发射端最优的预编码矩阵E=V。

接收端采用最小均方差准则(MMSE)信号检测，最佳解码矩阵D可以用(3)式表示。

D=[I+ρEHHHHE]-1EHHH

(3)

式中：I是单位矩阵，ρ是发射端信噪比。

从文献[12]可知，功率均匀分配条件下，信道的互信息量I可用式(4)表示。

(4)

式中：Hi是第i个子载波对应的信道矩阵函数，E(i)是Hi对应的预处理矩阵，(·)H表示矩阵共轭转置运算。

将频率选择性信道看成是准静态的，并且采用非各态历经随机过程来描述这类信息的变化，可以把将信道的互信息量定义为瞬时信道容量C[13]，并用式(5)来表征C大小。

(5)

式中：‖Q‖表示对矩阵Q求范数运算，Pi是第i个子载波的功率分配。

1.2.2 功率分配的优化 研究各子载波上的功率分配Pi，文献[11]对在空间分集MIMO-OFDM系统有详细研究，在不考虑子载波比特分配的条件下，功率分配的优化结果用式(6)表示。

(6)

式中：Hi是第i个子载波的信道，λmax[Q]表示矩阵Q的最大特征值，令OFDM每一帧子载波数为N，每个子载波的平均功率是1，OFDM发射总功率表示则为N。

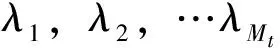
i,j∈S={ 1,2,…,N}

(7)

式中：Hi、Hj分别是第i、j个子载波的信道，λ[Q]表示矩阵Q的特征值，sum(λ[Q])表示矩阵Q各特征值之和。

1.2.3 功率分配量化和预编码联合优化 由于反馈信道资源非常有限，采用连续值表示的预编码矩阵和功率分配没有实用价值，必须对以上各个连续的优化值进行量化。文献[3,5]中预编码量化算法采用各子载波平均分配功率的方法，文献[10,11]对功率分配优化停留在连续值阶段。

文中提出的功率量化方法不同于现有算法：先设计一个离线功率码本，然后从码本中选取最优的元素。

根据文献[3,13]对频率选择性信道特性分析，对于带宽有限的信道，式(7)表达的最佳功率分配Pi明显集中平均功率系数附近，即Pi分布是以1为中心的随机分布，并且功率离中心越近其概率越大[3，13]，根据这个特征，为了减小量化误差，文中对Pi进行非均匀量化，参照非均匀量化理论中的A律近似原理[13]，提出对称的16段非线性折线算法，即设计码本ß的长度LB=16，各段折线的斜率变化，各段对应不同范围的功率Pi，具体数据在表1中列出，对应的折线图为图2。

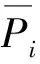
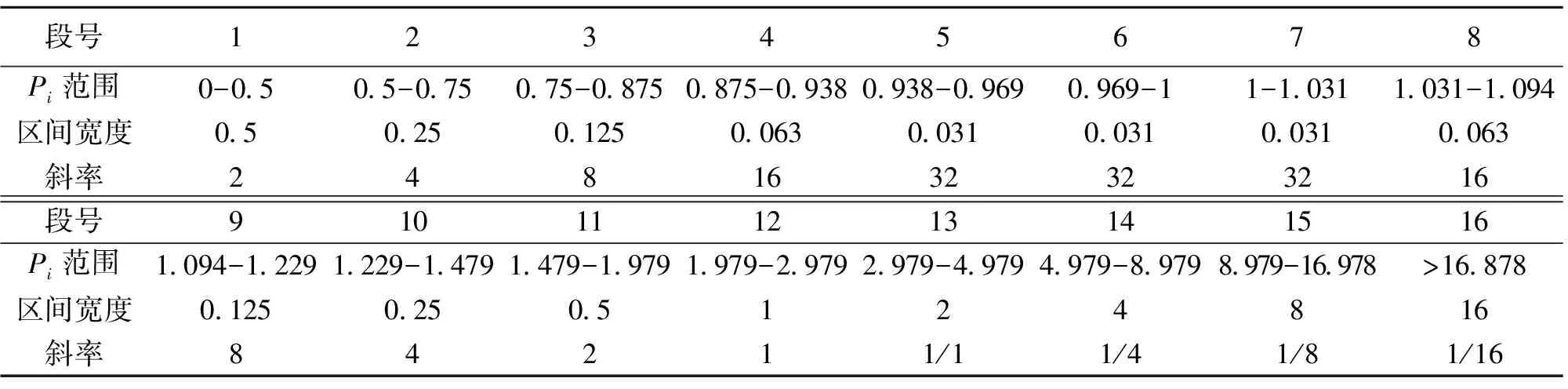
表1 16段折线量化数据分布1)

1)“段号”表示16个不同折线曲线的量化序号，“Pi范围”表示输入的连续功率系数范围，各段的宽度在“区间宽度”中表示，倾斜大小用“斜率”表示

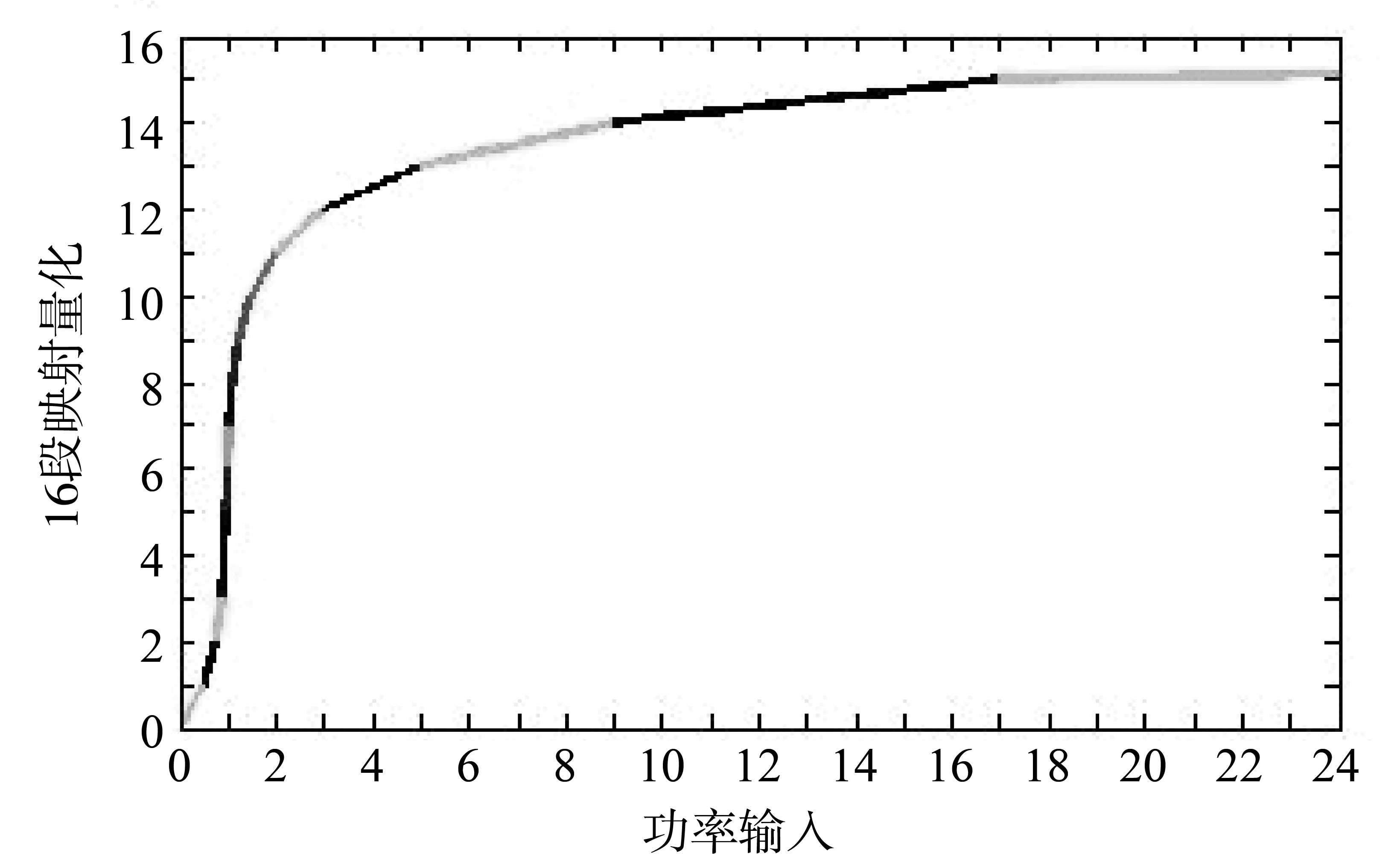
图2 非线性量化功率量化图Fig.2 Block diagram of MIMO-OFDM spatial multiplexing system

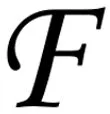
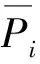
(8)

式中：det(·)表示求解行列的值。

1.2.4 发射端的插值恢复算法 为了进一步减少反馈比特数，文中改进了分组反馈算法，提出了基于分组反馈的功率分配和预编码矩阵联合量化优化算法，步骤如下：

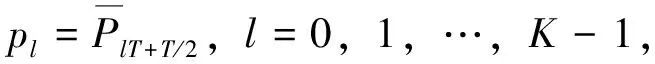
k=1,2,…,T-1

(9)

式中，ck=(k-1)/T是线性权重系数。

为了在发射端得到全部子载波的预编码矩阵，文中新设计了改进型矩阵插值表达式，如(10)式，对预编码矩阵插值引入角度调节因子Φl,k，由(11)式可见Φl,k不但考虑了θl-1和θl，而且考虑不同子载波的排序(即k不同)，该式不同于文献[5]中的矢量插值算法，也不同于文献[3]中的重复采用预编码矩阵码本矩阵求迹的复杂方法。

1≤l≤K,2≤k≤T

(10)

Φl,k= ej(θl-1 + kΔ ),Δ=(θl-θl-1)/(T-1)

(11)

(12)

式(10-12)中：El=ElT+1,0≤l≤K-1由(8)式而得，θl表示的角度变量通过搜索角度码本得到最佳值：θl∈{0,2π/P,…,2π(L-1)/L}。Θ={0,2π/L,4π/L,…,2π(L-1)/L}表示长度为L角度码本，在接收端通过式(12)对每组中第T/2个子载波优化，得到最优角度变量θl，并反馈对应的索引到发射端后，在发射端采用(10)插值得到全部子载波的最优预处理矩阵ElC+k。

2 方案反馈开销和算法复杂度进行分析

2.1 反馈比特量分析

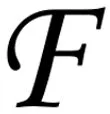
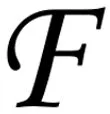
2)分组反馈算法：对每一个子载波组只反馈一个量化分集向量信息，每一帧反馈比特数等于Klog2LF=48；

3)分组反馈插值算法：充分兼顾到1)和2)两种算法优缺点的算法，一方面进行分组反馈；同时利用相关性对相邻子载波进行线性插值，还引入量化旋转角度进行格点搜索优化减小误码率。每组子载波反馈的比特包括量化分集向量比特log2LF和旋转角度比特log2L，每一帧反馈总比特数是Klog2LF+Klog2L=48+32=80；

4)文中算法：每组子载波反馈的比特除与3)中算法相同的信息外，还有量化功率比特log2LB，总数为K(log2LF+log2L+log2LB)=8×(6+4+4)=112。从反馈比特来看，其中全载波反馈算法开销最大，分组反馈算法最小，文中算法的比特开销比全载波反馈算法的比特数减少了70%，比分组反馈插值算法的略高。

2.2 计算复杂度分析

文中算法主要的计算量来自式(3)、(7)、(8)、(10)和(12)，计算中没有循环迭代，没有排序，而且非线性功率分配不存在矩阵运算，定性上看总的计算量并不大。文中算法每帧OFDM量化预编码搜索个数：N/K=8个；而现有的“全载波反馈算法” 每帧OFDM量化预编码搜索个数是N=64个。“分组反馈插值算法” 预编码搜索个数是N/K=8个。对于较多子载波的MIMO-OFDM系统来说，文中算法对比“全载波反馈算法”复杂度也是大大降低。

3 系统仿真和分析

利用Monte Carlo仿真方法，仿真过程中选用ESTI/BRAN Model A信道模型，子载波数N=64，OFDM每帧包含K=8组，OFDM循环前缀长度GI=8，分别比较全载波反馈算法、分组反馈算法和分组反馈插值算法与文中算法在误码率和信道容量两方面的特性。

3.1 误码率特性

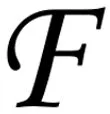
从图3可知，在BER=10-4时，文中算法与分组反馈插值算法相比获得1 dB的信噪比增益，文中算法对比分组反馈算法提高4 dB的信噪比增益；在信噪比SNR=9 dB时，文中算法误码率仅仅是分组反馈插值算法误码率的20%，对比分组反馈算法，文中的算法的BER性能优势更加明显。对比全载波反馈算法尽管文中算法略高，但反馈比特数仅占全载波反馈算法比特数的30%。

图3 量化误码率比较(Mt=3，Mr=3)Fig.3 Comparison of quantified BER performance of system(Mt=3，Mr=3)

3.2 系统的信道容量

根据式(5)定义的预编码系统瞬时信道容量C，比较现有三种算法与文中算法的信道容量。

图4给出了在发射天线和接收天线数Mt=3，Mr=3条件下信道容量，可见在信噪比SNR=10 dB时，文中算法的信道容量比分组反馈插值算法提高了4 b/s，并且随着信噪比SNR增加，文中算法优于分组反馈算法和分组反馈插值算法的趋势更明显。因此说，文中算法能实现的信息传输速率更快，信道容量更大。

图4 OFDM系统信息速率(Mt=3，Mr=3)Fig.4 Capacity of MIMO-OFDM system(Mt=3，Mr=3)

4 结 论

针对空间复用下行MIMO-OFDM系统，文中优化了一种子载波功率分配的表达式，设计一种非线性功率量化码本，提出一种基于分组反馈的量化功率分配和量化预处理矩阵的联合预处理方法，通过查表得到了功率量化反馈比特信息，发射端利用这些反馈信息通过插值就可以恢复优化功率分配和发射预编码矩阵，从而实现了联合量化发射预处理。总之，文中算法在反馈信息特数增加不多情况下，实现误码率大幅下降，信道容量增加，综合特性比现有算法明显更好。

参考文献：

[1] WANG Z, GIANNAKIS G B. Wireless multicarrier communications:where Fourier meets Shannon[J]. IEEE Trans on Signal Process. 2000,17(3): 29-48.

[2] ANTONIO G, ANA B. Optimizing average performance of OFDM systems using limited-rate feedback[J]. IEEE Trans on Wireless Commun, 2010,9(10):3130-3143.

[3] CHOI J, HEATH Jr R W. Interpolation based unitary precoding for spatial multiplexing MIMO-OFDM with limited feedback[J]. IEEE Trans on Signal Processing, 2006,54(12): 4730-4740.

[4] FU Hongliang, TAO Yong. Nonlinear precoding for spatial multiplexing MIMO-OFDM downlink systems[C]∥ 2010 2nd International Conference on Signal Processing Systems (ICSPS). Dalian, China July 5-7, 2010:116-119.

[5] CHOI J, MONDAL B. Interpolation based transmit beamforming for MIMO-OFDM with limited feedback[J]. IEEE Trans on Signal Processing , 2005,53(11): 4125-4135.

[6] ARIYAVISITAKUL S，ZHENG J，OJARD E. Subspace beamforming for near-Capacity MIMO performance[J]. IEEE Trans on Signal Process, 2008, 56( 11):5729-5733.

[7] Time-domain transmit beamforming for MIMO-OFDM systems with finite rate feedback[J].IEEE Trans on commun,2009, 57(9)：2828-2838.

[8] 许道峰,杨绿溪. TDD-MIMO下行链路预编码[J]. 通信学报，2009，30(5):35-41.

[9] GHADERIPOOR A, TELLAMBURA C. On the design, selection algorithm and performance analysis of limited feedback transmit beamforming[J]. IEEE Transactions on Wireless Communications, 2008,7(12):4948-4957.

[10] LEINONEN J, HAMALAINEN J. Performance analysis of downlink OFDMA resource allocation with limited feedback[J]. IEEE Trans on Wireless Communications, 2009, 8(6):2927-2937.

[11] PAN Yahan, AISSA S. Dynamic resource allocation with beamforming for MIMO OFDM systems: performance and effects of imperfect CSI[J]. IEEE Transactions on Wireless Communications, 2007,6(12):4249-4255.

[12] FILIPPO Z, WANG Xiaodong. Low-rate-feedback-assisted beamforming and power control for MIMO-OFDM systems[J]. IEEE Trans on Vehicular Technology, 2010,59(1):225-234.

[13] PROAKIS J G . 数字通信[M]. 5版.北京: 电子工业出版社,2009: 183-200.