共形粘合的有界度圆填充逼近
陈德健,蓝师义
(广西民族大学理学院,广西 南宁 530006)
圆填充是指具有特定相切模式的一种圆格局,其理论在复分析与离散几何的交叉学科中是当今一个快速发展的研究领域。近几年来在这个领域研究所取得的成就起源于Fields奖得主Thurston[1]在1985年提出这样的猜测:六边形圆填充可用来近似Riemann映射。1987年Rodin等[2]证明了该方案的收敛性。 随后出现大量关于圆填充理论及其应用的研究(见文[3-6]等)。共形粘合最近重新引起人们的研究兴趣,是因为它在图像识别和弦理论研究中有着重要的应用。例如,Mumford等[7]用共形粘合作为关键步骤来研究图像识别方法;Radnell[8]证明了有界Riemann曲面的拟对称粘合可以给弦理论提供一个模型;Williams[9]用离散粘合技术构造了三角剖分曲面的共形映射。
对共形粘合的离散逼近的研究,Williams[10]已经建立了共形粘合的六边形圆填充离散逼近。在本文,我们将Williams的结果推广到非六边形圆填充即有界度圆填充的情形。首先,我们讨论平面内两个不相交圆盘的共形粘合。从复平面内无限有界度圆填充的载体我们可以构造这两个圆盘的近似区域,将组合粘合技术应用于这两个近似区域,我们得到球面上的一个三角剖分。根据圆填充定理,就得到Riemann球面上一个相关的圆填充。由此我们可建立两个离散近似映射。然后,证明了它们分别收敛于由一个拟对称诱导的两个共形粘合映,并且散粘合曲线也收敛于该拟对称诱导的拟圆周;其次,我们研究上半平面与下半平面的共形粘合。应用两个有限正方形区域序列分别近似上半平面与下半平面,对于每一对正方形区域,类似于前面的做法,我们可以得到它们的有界度圆填充离散近似区域,对这两个近似区域应用组合粘合方法就得到一个拓扑圆盘的三角剖分,这就给出复平面上一个相关的圆填充。基于此,我们就可以建立两个离散近似映射,然后推出它们的收敛性。
本文工作与文[10]的主要不同是:第一,构造离散共形粘合所使用的圆填充不同,文[10]应用六边形圆填充即每个圆的周围都有六个相邻圆,而我们应用有界度圆填充,也就是每个圆的周围不一定都有六个相邻圆,但只要其相邻圆的个数有界就可以; 第二,所粘合的区域不一样,我们将文[10]所讨论的单位圆盘与单位圆盘外部的离散粘合推广到复平面内任意两个相交圆盘的情形。本文组织如下:在第1节给出圆填充与共形粘合的基本概念及一些相关结果;在第2节讨论平面两个不相交圆盘的离散共形粘合;上半平面与下半平面的离散共形粘合在第3节讨论。
1 圆填充与共形粘合
在这一节我们将简要给出圆填充与共形粘合的基本概念及其相关结果,更详细的背景知识,可参见文[6,11]等。
定义1 给定一个三角剖分K,我们称复平面内一个圆集合P为关于K的圆填充, 若下面条件成立:
(i) 对于K中每个顶点u,在P中都有一个圆Cu与之对应;
(ii)若[u,v]是K的一条边,则圆Cu与Cv外切;
(iii) 若u,v,w是K内的一个正向面,则Cu,Cv,Cw组成P中一个正向的两两相切的三个圆。
一个圆填充称为单叶的, 如果它所有的圆都不重叠, 也就是没有两个圆相交多于一点。 一个圆填充称为有界度圆填充,若其每个圆的相邻圆的个数都小于或等于某个常数。用测地线连接圆填充P中所有相切圆的中心所形成的几何复形称为P的载体,记为carr(P),也称为复形K在欧式平面上的嵌入。
关于圆填充的存在唯一性,我们给出下面本文将用到的两个结果,它们可以从文[6]得到。

命题2 一定存在复平面内无限的有界度单叶圆填充P,使得其载体填满整个复平面,即carr(P)=。
定义2 给定两个Jordan区域D1和D2以及它们边界上的一个同胚映射φ:∂D1→∂D2, 如果等同点x∈D1与φ(x)∈D2,那么就可以把D1和D2粘合在一起。进一步,若存在两个共形映射f:D1→Ω与g:D2→Ω*,使得在边界上有g=f∘φ,其中Ω和Ω*分别为Riemann球面S2内某一条Jordan曲线Γ的有界分支与无界分支,则称φ为一个共形粘合。
定义3 设D和D*是复平面内的两个圆盘,映射φ:∂D*→∂D是一个保向同胚映射。若一个存在常数K,使得∂D*上任意具有相同长度(|I|∂D*=|J|∂D*)的两个相邻的子区间I与J,有则称φ为一个K拟对称映射。
定义4 设Γ1和Γ2是复平面内的两条Jordan曲线,称映射φ:Γ1→Γ2为一个K-双lipschitz同胚映射,若对所有x,y∈Γ1,有
容易知道,任意一个K-双Lipschitz映射都是一个K2-拟对称映射。关于两个区域的共形粘合问题,有下面著名结果,也称为共形粘合定理,它可由文[11]得到。
命题3 (共形粘合定理) 设D,D*⊂是两个不相交的圆盘,φ:∂D*→∂D是一个拟对称映射,则存在两个共形映射f:D→Ω和g:D*→Ω*,使得它们在边界上满足g=f∘φ,这里Ω与Ω*是S2上某一条Jordan曲线的两个分支。
本文的主要目标是应用有界度圆填充方法构造命题3中f与g的离散近似映射,并证明它们的收敛性。
2 圆盘粘合的离散近似
在这一节我们将讨论两个拓扑圆盘的离散共形粘合。也就是,我们应用有界度圆填充技术构造两个圆盘粘合的离散近似映射,然后证明这些离散粘合映射收敛于共形粘合映射。 这分为下面三个步骤进行。
第一步,首先描述两个三角剖分的组合粘合。设T和T*是两个拓扑圆盘的三角剖分, 且假设它们被嵌入到复平面内,使得它们的每个三角形都是欧氏三角形。将T的边界顶点,按逆时针记为v1,v2,…,vn,T*的边界顶点按顺时针记为w1,w2,…,wm。设φ:∂T*→∂T是一个K-双lipschitz同胚映射。为了确保T*中每个边界顶点在φ下的像都是T中某一边界顶点,因此,我们需要对T*的每个边界顶点ωi(i=1,2,…,m)按下面添加一个顶点



引理2 假设三角剖分T和T*的每个三角形的内角都属于区间[α,β],其中0<α≤β<π是两个常数。则它们的扩张三角剖分T*和T中每个面的内角θ也属于某区间[α*,β*],这里0<α*≤β*<π仅依赖于α,β,K和比率C=l/l*,而l和l*分别表示T和T*中包含一个边界顶点的边的最大长度和最小长度。
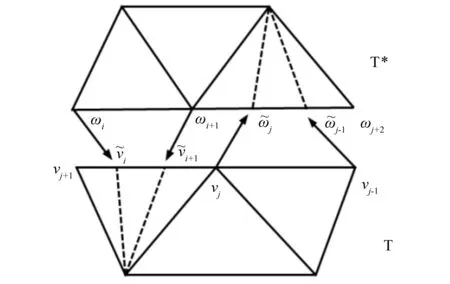
图1 两个三角剖分的组合粘合 Fig.1 Combinatorial welding of two triangulations
第二步,用有界度圆填充构造两个圆盘的离散近似区域。考虑复平面内如命题3中两个不相交的圆盘D与D*。根据命题2,我们知道,必存在一个填满整个复平面的有界度无限单叶圆填充Q,不妨假设Q中每个圆的半径不超过1/(2n),其中n∈。设QD是包含于D内的Q的最大子圆填充,记其载体carr(QD)=Tn。令Dn表示Tn的多面体,则Dn⊂D为D的一个离散近似区域,如图2所示。完全类似地,我们可以得到包含于D*内的一个三角剖分及其相应的离散近似区域并取定的一个内部顶点为w∞。容易知道,当n→∞时,
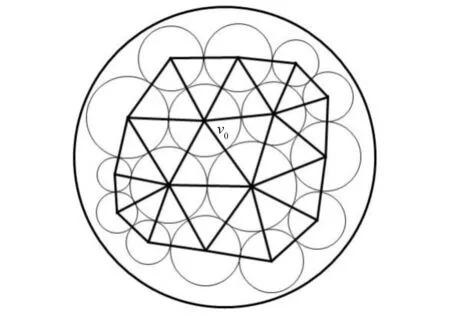
图2 一个圆盘D的离散近似区域Dn的构造Fig.2 The construction of discrete approximating regions Dnof a disc D



(ii)对每一个n∈,fn与gn都是K1-拟共形映射,这里K1-只依赖于圆填充Q的度;
(iii)对每一个n∈,曲线Γn是K2-拟圆周,其中而K2仅依赖于常数K和圆填充Q的度。
定理1 给定复平面内两个不相交的圆盘D和D*, 设φ:∂D*→∂D是一个双Lipschitz拟对称映射,则存在离散近似映射序列fn和gn分别在D和D*的紧子集上一致收敛于由φ诱导的共形粘合映射f和g,当n→∞时。而且当n→∞时,离散粘合曲线Γn收敛于由φ诱导的拟圆周Γ。

其次,根据引理 3 (ii),我们知道,对于每一个n∈,fn和gn都是K1-拟共形映射。 由欧氏平面圆填充的面积长度引理[2],用类似于文[12-13]的方法, 我们可以推出当n→∞时,fn:Dn→Ωn与分别在D与D*的紧子集内一致收敛于共形映射f:D→Ω和g:D*→Ω*。
最后, 注意到对于每个n∈, 成立同时当n→∞时, (pn)-1与分别收敛于恒等映射。因此,我们推出当n→∞时,φn一致收敛于φ。这样在引理3(i)中令n→∞,我们就得到g=f°φ.此外,引理3(iii)给出了对于每个n∈,Γn是一个拟圆周,再根据环引理[2],我们可以推出Γn一致收敛于某一个拟圆周Γ, 当n→∞时。 于是就完成了这个定理的证明。
如果把上面定理中的双Lipschitz映射φ改为是一个拟对称映射,则结论也成立。也就是以下定理。
定理2 给定复平面内两个不相交的圆盘D和D*,设φ:∂D*→∂D是一个拟对称映射,则存在离散近似映射序列fn和gn分别在D和D*的紧子集上一致收敛于由φ诱导的共形粘合映射f和g,当n→∞时。而且当n→∞时,离散粘合曲线Γn收敛于由φ诱导的拟圆周Γ。
证明 根据文[11,14],我们知道,双Lipschitz映射在所有拟对称映射组成的集合中是稠密的,由此,我们推出该定理成立。
3 半平面粘合的离散近似
在这一节我们将应用有界度圆填充技术构造上半平面U与下半平面L粘合的离散近似映射,然后,证明它们的收敛性。
首先,构造离散近似映射。设φ是上的一个K-双Lipschitz拟对称映射使得0和∞是它的两个不动点。对每个n∈,用a与b分别表示满足下面条件的1/n的两个最小倍数:a≤φ(-n),φ(n)≤b。如在第3节假设Q为填满整个复平面的无限有界度单叶圆填充且Q中每个圆的半径小于或等于1/n。用TUn和TLn分别是包含于区域[a,b]×[0,b-a]和[-n,n]×[-2n,0]中的 carr(Q)的两个最大子复形。将TUn中位于0和1的顶点分别记为v0和v1,且用Ln和Un分别表示TLn和TUn所形成的多面体区域。上面的条件保证了TLn∩的顶点在φ下的像位于TUn∩的边上,应用第3节的粘合方法,通过φ我们分别TUn和TLn扩张为Un和Ln。


其次,证明离散近似映射fn和gn的收敛性。因为φ是一个保向的实同胚,所以φ在上递增的。由此,我们得到,当n→∞时,a→-∞,b→+∞且Ln∪Un→。由假设φ是双Lipschitz映射,而Kn是有界度的,因此fn和gn均是K1-拟共形映射,其中K1不依赖于n。同时,由构造我们推出,等式gn=fnφn在[-n,n]成立。进一步,我们有
引理4 近似映射fn和gn都能通过成为扩张的K-拟共形映射。而且,对于给定的任意紧子集E,则当n充分大时,映射fn和gn在E上都有定义。
由Un的构造我们知道,当n→∞时,Un→U。 因此,对于给定的紧子集E,当n足够大时,Un将覆盖为了保证fn在上有定义,下证对足够大的n,Φn(Ln)也将覆盖由Beurling-Ahlfors扩张的构造[16]知,当n→∞时,Φn局部一致收敛于Φ,其中Φ是φ的Beurling-Ahlfors扩张。因此,对每个i=1,2,…,Φ(Li)必包含0的一个相对开邻域假设Ri是这样一个开邻域的最大半径。则因为Φ是真映射且当n→∞时Ln→L,所以必有Ri→∞,当i→∞时。然而,由于Li是紧的,因此Φn在Li上一致收敛于Φ。于是,对每个i,一定能找到Ni∈,使得对所有n≥Ni,有特别地,对所有n≥Ni,有
⊂Φn(Ln)

由于每个fn都使得0和1为不动点而忽略∞,因此由文[11]我们知道,{fn}是正规族且存在一个子序列局部一致收敛于上的一个K-拟共形同胚映射f。通过重新组合,我们可假设整个序列{fn}收敛于f。因为f的定义域是整个复平面,所以Liouville’s定理给出f的值域也是整个复平面。事实上,通过令f(∞)=∞可以使∞为f的可去奇点,于是f(∪{∞})是在S2上过0,1和∞的一条Jordan曲线。
根据fn的构造和圆填充的环引理,我们推出当n→∞时,fn在U的任意紧子集上的最大伸缩商趋近于1。由此我们得到f在U上是共形的。同理,我们推出{gn}也收敛于L上的一个共形映射g。从而我们有
定理3 若给定一个双Lipschitz拟对称映射φ,则一定存在两个离散近似映射序列fn和gn分别在U和L的紧子集上一致收敛于由φ诱导的共形粘合映射f和g。而且,由fn和gn的像的公共边界形成的离散粘合曲线Γn是一个拟圆周,它一致收敛于由φ诱导的拟圆周Γ。
证明由于f和g在上是K-拟共形的,因此f(∪{∞})=g(∪{∞})是一个拟圆周。另外,注意到对每个n∈,有gn=fnφn,并且fn,gn和φn在上分别一致收敛于f,g和φ,所以我们有g(x)=fφ(x),x∈。
根据共形粘合定理的唯一性, 我们知道f|U和g|L必是对应于φ的两个共形粘合映射。这蕴含着原来构造的两个序列{fn} 与{gn}的收敛性。由引理4我们知道, {fn} 与{gn}都是拟共形映射,于是Γn是一个拟圆周。此外,由构造我们知道,f|L与g|U分别为粘合映射f与g通过Γ的扩张。因此由fn和gn在上的一致收敛性推出Γn也一致收敛于Γ,当n→∞时。这样我们就完成了这个定理的证明。
参考文献:
[1] THURSTON W. The finite Riemann mapping theorem [C]//Invited address, International Symposium in Celebration of the proof of the Bieberbach Conjecture, Purdue University, 1985.
[2] RODIN B, SULLIVAN D. The convergence of circle packings to the Riemann mapping [J]. J Differential Geom, 1987, 26:349-360.
[3] MARDEN A, RODIN B. On Thruston’s formulation and proof of Anndreev’s theorem [J]. Lecture Notes in Math, 1990, 1435: 103-115.
[4] STEPHENSON K. The approximation of conformal structures via circle packing [J]. Computational Methods and Function Theory, Ser Approx Decompos, Volume 11, World Sci Publishing, River Edge, NJ, 1999: 551-582.
[5] HE Z X, SCHRAMM O. Hyperbolic and parabolic packings [J]. Discrete Comput Geom, 1995, 14: 123-149.
[6] STEPHENSON K. Introduction to circle packing (the theory of analytic functions) [M]. Cambridge: Cambridge University Press, 2005.
[7] SHARON E, MUMFORD D. 2D-Shape analysis using conformal mapping [J]. Intern J Comput Vision, 2006, 70: 55-75.

[9] WILLIAMS G B. Constructing conformal maps of triangulated surfaces [J]. J Math Anal Appl, 2012, 391(1): 113-120.
[10] WILLIAMS G B. Discrete conformal welding [J]. Indiana Univ Math J, 2004, 53(3): 765-804.
[11] LEHTO O, VIRTANEN K I. Quasiconformal mappings in the plane [M]. New York: Springer-Verlag, 1973.
[12] HE Z X, RODIN B. Convergence of circle packings of finite valence to Riemann mappings [J]. Comm in Aanl and Geom, 1993, 1: 31-41.
[13] LAN S Y, DAI D Q.C∞-convergence of circle packings of bounded degree to the Riemann mapping [J]. J Math Anal Appl, 2011, 376: 1-10.
[14] KELINGOS J A. Boundary correspondence under quasiconformal mappings [J]. Michigan Math J, 1966, 13: 235-249.

[16] BEURLING A, AHLFORS L. The boundary correspondence under quasiconformal mappings [J]. Acta Math, 1956, 96: 125-142.

