关于高效调制成形滤波器的中心频率
陈志敏 吴乐南
(东南大学信息科学与工程学院,江苏 南京 210096)
引 言
世界范围内的频谱资源短缺挑战着科研人员和运营商的智慧,研究高频谱利用率的调制技术以最大限度地压缩无线传输频谱,具有直接的经济效益和重要的战略意义[1].超窄带(Ultra Narrow Band,UNB)调制作为一种高频谱利用率的通信新技术,最初由美国的H.R.Walker博士1980年提出[2],此后技术创新[1,3]与专利争夺[4]主要在中美两国展开.在众多的UNB高效调制技术中,以扩展的二元相位键控(Extended Binary Phase Shift Keying,EBPSK)[1]为代表的不对称二元偏移键控(Asymmetry Binary Shift Keying,ABSK)调制[4]简单高效,得到了较多的关注[5-10].EBPSK调制信号功率谱的特点是:大部分功率集中在载波及其附近,被拔高为“频谱树”;剩余的小部分信号功率则分布在一个相当宽的频率范围,被压低成“频谱草”.然而,尽管这样的信号即使不采用专门的成形滤波,在无线电管理部门现行的带宽定义下也堪称“超窄带”[1],但却不可能完整地通过发射系统,因为功放级的调谐网络以及馈线、天线等的带宽都是有限的.另外,虽然在严格的同等带宽限制下,EBPSK系统也表现出了优良的传输性能[11],但由于EBPSK功率谱关于其载频是不对称的,因此其成形滤波器或发射端综合频率响应的中心频率是否应与其载频重合,尚无结论.
为此,本文首先简要介绍EBPSK调制与解调技术,推导已调信号功率谱中非载频处的功率谱表达式,发现EBPSK调制信号的能量最大处的频率偏离其载频;进而在不同带宽范围下对EBPSK调制信号发送功率的百分比进行仿真对比;最后将发送成形滤波器的中心频率相对于EBPSK载频偏移后进行系统的解调性能仿真,得到了中心频率偏调可带来系统增益的结论.
1 EBPSK调制与解调
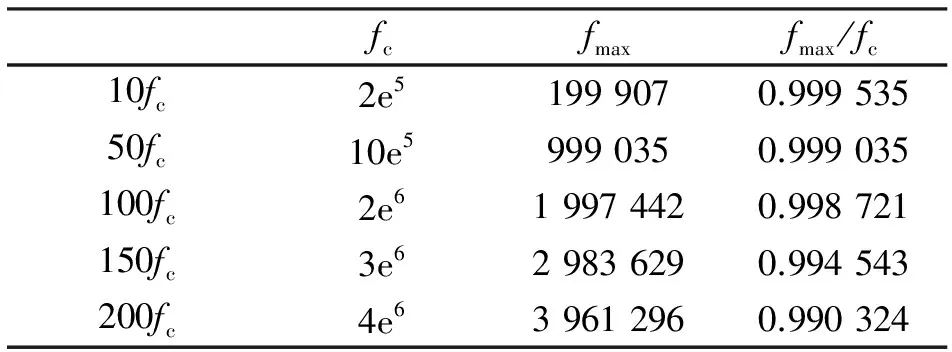
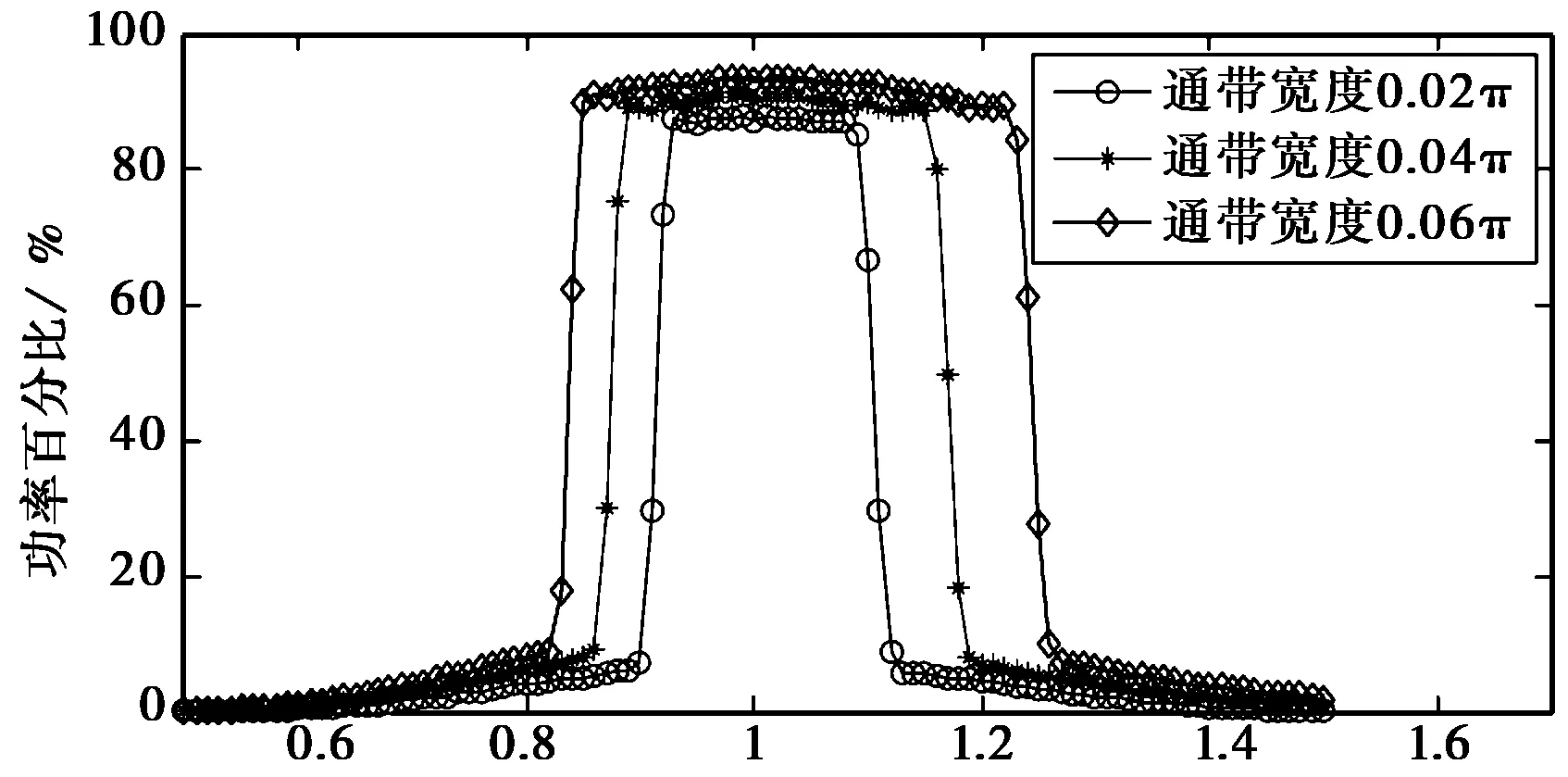
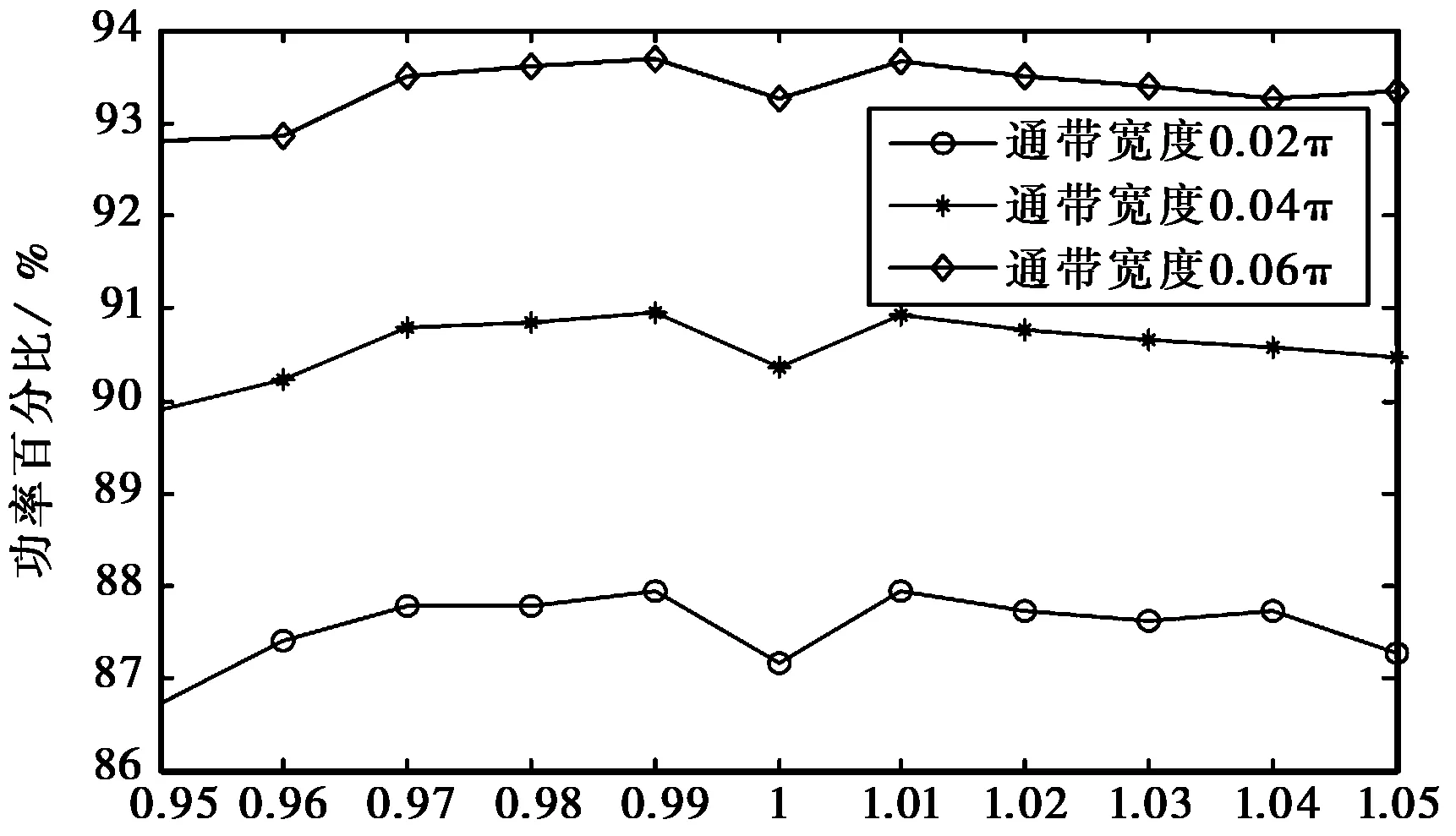
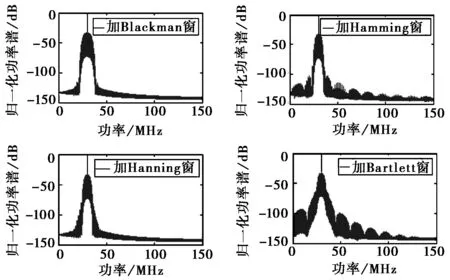
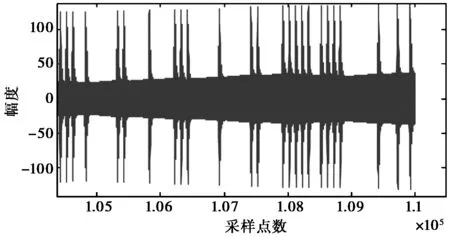
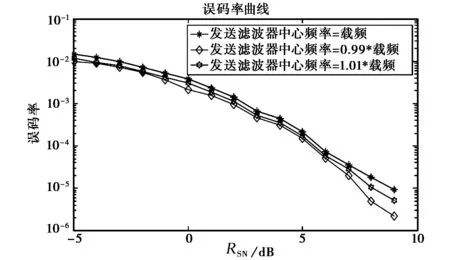
传统的二元相位键控(Binary Phase Shift Keying,BPSK)调制“0”和“1”是对称的,且调制角度θ=π,因此能够完全抑制载波,但其频谱利用率理论上只有1 bps/Hz;而EBPSK即使取调制角度θ=π,也仍然保留了较高的载波分量,因为其调制时段τ持续了K个载波周期,而码元长度T则持续了N个载波周期,要求K (1) f0(t)和f1(t)分别为数据“0”和“1”的信号波形,且只在时段τ内才可能不同,为了放大这种微小差异,可利用一类特殊的无限冲激响应(Infinite Impulse Response,IIR)数字带通滤波器,使得与之匹配的EBPSK调制信号的滤波输出波形在信息调制处产生明显而强烈的寄生调幅冲击,在噪声背景下突显出信号的调制信息[12],称之为冲击滤波器.EBPSK调制及冲击滤波器输出波形如图1所示. 图1 EBPSK调制波形和冲击滤波器输出波形 从图1可以看出,码元“1”持续的K个载波周期经过接收机冲击滤波后转化为寄生调幅,且寄生调幅仅出现在跳变周期中.因此,采用简单的幅度门限就可直接对信息码元做出判决,无需下变频到基带或零中频. EBPSK调制波形的功率谱,已有文献[5-13]推导,本文直接引用其结论.令θ=π,则可得EBPSK调制信号的功率谱中: 1) 载波分量为 (2) 2) 非载波分量为 (3) 式(2)、(3)显示EBPSK信号的功率谱由连续谱和离散谱构成,其中离散谱给出了EBPSK已调信号的周期成分,不含调制信息;而连续谱则体现了调制信息的随机性. 令B=A= 1,并取fc= 465 kHz,K=2,N=20,则载波功率谱为 (4) 式中,τ和T的含义同式(1). 非载波信号功率谱为 (5) 在理论计算的非载频处EBPSK调制信号功率谱表达式(3)中包含了无限冲击函数δ(f),因而为了给出理论功率谱,对δ(f)进行了幅度近似,其近似值仅影响连续谱最高点的高度,对整体包络形状没有影响.功率谱的理论值是在假设样本数据无限长的前提下精确计算的结果,其理论功率谱图如图2所示. 由图2可见,非载频处EBPSK调制信号功率谱的最大值在载频附近,其是否关于载频对称直接影响到EBPSK调制信号功率谱的对称性.理论值假设样本数据为无限长,因此取尽量多的点进行近似处理,以取得功率谱最大值的位置.设置仿真截止频率分别为10fc,50fc,100fc,150fc,200fc.EBPSK调制信号非载频处功率谱最大值fmax与fc的位置关系如表1所示. 表1 非载频处功率谱最大值fmax与fc的位置关系 由表1可见,随着采样点数的增加,非载频处功率谱与载频的相对位置关系越趋于固定值,约为0.99.说明EBPSK调制信号的功率谱分布并非以载频为中心对称.下面据此进一步讨论发送滤波器的设计. 无疑,只有空中频谱才可能干扰别人,才占用公共资源,才应该有偿使用,才必须合理监管[1].因此,为了通过成形滤波进一步紧缩发射信号的空中频谱,获得更高的频谱利用率,并保证带内输出功率的最大化,本节对通过3种不同带宽有限冲激响应(Finite Impulse Response,FIR)滤波器的EBPSK信号的输出功率百分比进行了仿真分析,结果如图3所示.由图3(a)可以看出:不同通带宽度对应的功率百分比曲线走向趋势大致相同,均在载频的对称邻域内具有高输出功率比,且因EBPSK调制信号自身的能量高度集中于载波,载频附近不同带宽的功率百分比均在90%左右.图3(b)为载频处的局部放大图,观察发现3种带宽下的输出功率百分比最大处均位于载频左右两侧的0.99和1.01处,而载波频率却处于相对低点,其中0.99倍载频比1.01倍载频处又略微偏高,这与表1的分析相吻合,因此首选0.99倍载波频率作为发送滤波器的中心频率. (a) 成形滤波后信号输出百分比 (b) 成形滤波后信号输出百分比(局部)图3 成形滤波后EBPSK调制信号功率百分比 发送滤波器中心频率确定后,接下来是窗函数的选择,这对滤波特性影响很大,一般要满足:1)主瓣窄,以获得较陡的过渡带;2)旁瓣尽可能低.实用中这两点往往不能兼得,参考表2知,可通过增加主瓣宽度来换取对旁瓣的抑制. 表2 窗函数窗口长度M与阻带衰减的对应关系 从表2可见,4种窗函数中Bartlett窗、Hanning窗和Hamming窗的近似过渡带宽相同,均较Blackman窗窄.同时,Hamming窗的最小阻带衰减与前两种窗函数相比较而言,第一旁瓣的衰减更大,能量更加集中在主瓣.对于超窄带通信系统而言,发送成形滤波器的窗函数需具备大的带外衰减以及较窄的窗口宽度,才能使能量更加集中,频率利用率更高. 基于Blackman窗、Hamming窗、Hanning窗和Bartlett窗的Welch谱估计得到加窗后的EBPSK调制信号功率谱图,如图4所示.仿真参数:fc= 30 MHz,A=B= 1,K=2,N= 100,采样频率为300 MHz.4种窗函数均为50阶,归一化通带宽度为0.02π. 根据前面的分析,定量比较各窗函数的性能,一般根据三个频域指标进行衡量:3 dB带宽、最大旁瓣峰值、旁瓣谱峰渐进衰减速度.对于EBPSK调制信号来说,其功率谱呈现“树+草”的形式,用3 dB带宽标准来衡量不足以区分各窗函数的优劣.因此,采用主瓣宽度Bw/MHz,第一旁瓣衰减D/ (dB/oct)以及99%功率带宽B99%/MHz这3个频域指标进行各窗函数性能的比较.4种窗函数的性能对比如表3所示.可见,Hamming窗具有较大的旁瓣衰减以及较窄的主瓣宽度,更符合超窄带通信系统的要求. (a) 整体功率谱 (b) 中心局部放大的功率谱图4 基于Welch谱估计得到的EBPSK调制信号功率谱 窗函数BwDB99%Bartlett窗10-9014Hanning窗10-10512Hamming窗10-11513Blackman窗15-8017 发送成形滤波器的设计是否合理,最终还要由系统的解调性能来考核.采用基于Hamming窗的FIR发送成形滤波器,阶数为50阶,归一化通带宽度为0.02π.通过该FIR滤波器成形滤波发送的EBPSK调制信号,通过接收机的冲击滤波器后输出的时域波形如图5所示.改变调制端发送成形滤波器的中心频率,得到EBPSK解调器的误码性能如图6所示. 由图6可以看出,发送滤波器中心频率相对于EBPSK信号载频适当偏调可获得比准确调谐更好的解调性能.例如当误码率为10-5时,以发射信号载频为基准,发送滤波器中心频率向高偏10%约可取得0.8 dB信噪比增益,而向低偏10%则约有1.2 dB信噪比增益.这也验证了第2、第3节理论分析与仿真结果的正确性. 图5 加窗后EBPSK调制信号滤波输出波形 图6 成形滤波器不同中心频率系统误码性能对比 本文的分析与仿真表明: 1) EBPSK调制信号的能量并非以载频为中心对称分布. 2) 选择50阶加Hamming窗的发送成形滤波器且中心频率相对于EBPSK信号载频偏移10%,在10-5误码率下得到约1 dB的信噪比增益,其中将滤波器中心频率向低偏调增益更高. 3) 发送成形滤波器能够在紧缩EBPSK信号带宽的同时,保证甚至提高信息的传输性能. 本文只是研究了近似矩形的FIR发送成形滤波器,下一步将研究具有单峰幅频特性的IIR成形滤波器的偏调影响,这更符合发射机功放调谐回路和天馈线均为模拟系统的实际情况. [1] 吴乐南. 超窄带高速通信进展[J]. 自然科学进展, 2007, 17(10): 143-149. WU Lenan. Progress in ultra narrow band communication[J]. Progress in Natural Science, 2007, 17(10): 143-149. (in Chinese) [2] WALKER H R. Ultra Narrow Band Modulation Textbook [M/OL].[2012-08-20] http://www.vmsk.org/. [3] FENG Man, WU Lenan. Special non-linear filter and extension to Shannon’s channel capacity[J]. Digital Signal Processing, 2009, 19(5): 861-873. [4] WU Lenan, FENG Man, et al. Recent patents on ultra narrow band modulations[J]. Recent Patents on Signal Processing, 2011, 1(1): 36-47. [5] FENG Man, QI Chenhao, WU Lenan. Analysis and optimization of power spectrum on EBPSK modulation in through-efficient wireless system [J]. Journal of Southeast University: English Edition, 2008, 24(2): 143-148. [6] 王红星, 王洪利, 张 磊, 等. EBPSK及其优化调制信号的二阶循环平稳特性分析[J]. 电波科学学报, 2010, 25(1): 42-46. WANG Hongxing, WANG Hongli, ZHANG Lei, et al. Cyclostationarity analysis on EBPSK and its optimization[J]. Chinese Journal of Radio Science, 2010, 25(1): 42-46. (in Chinese) [7] 王红星, 王洪利, 毛忠阳. 基于时频分布的扩展的二元相移键控信号解调算法[J]. 吉林大学学报:工学版, 2011, 41(5): 1491-1496. WANG Hongxing, WANG Hongli, MAO Zhongyang. Analysis of EBPSK demodulation algorithm based on time-frequency distribution[J]. Journal of Jilin University: Eng and Technol Ed, 2011, 41(5): 1491-1496. (in Chinese) [8] 王红星, 王洪利, 毛忠阳,等. 基于循环谱特性的扩展二元相移键控解调算法[J]. 电波科学学报, 2010, 25(5): 934-939. WANG Hongxing, WANG Hongli, MAO Zhongyang, et al. The demodulation algorithm for EBPSK based on cyclic spectrum characteristic[J]. Chinese Journal of Radio Science, 2010, 25(5): 935-939. (in Chinese) [9] WU Lenan, FENG Man. On BER performance of EBPSK-MODEM in AWGN channel[J]. Sensors, 2010, 10: 3824-3834. [10] 戚晨皓, 陈国强, 吴乐南. 二阶锁相环的EBPSK信号解调分析[J]. 电子与信息学报, 2009, 31(2): 418-421. QI Chenhao, CHEN Guoqiang, WU Lenan. EBPSK demodulation analysis based on second-order phase locked loop[J]. Journal of Electronics & Information Technology, 2009, 31(2): 418-421. (in Chinese) [11] 何善宝, 林益明, 吴乐南, 等. 星间链路新型信号体制设计[J]. 中国空间科学技术, 2011, (4): 15-22. HE Shanbao, LIN Yiming, WU Lenan, et al. Design of new signal system for inter-satellite links[J]. Chinese Space Science and Technology, 2011, (4): 15-22. (in Chinese) [12] 冯 熳, 高 鹏, 吴乐南. 超窄带调制信号的特殊滤波分析与仿真[J]. 东南大学学报:自然科学版, 2010, 40(2): 227-230. FENG Man, GAO Peng, WU Lenan. Analysis and simulation of special filtering based on ultra narrow band modulated signal[J]. Journal of Southeast University: Natural Science Edition, 2010, 40(2): 227-230. (in Chinese) [13] 张士凯, 吴乐南. EBPSK调制信号功率谱分析[J]. 电波科学学报, 2008, 23(3): 496-500. ZHANG Shikai, WU Lenan. PSD analysis of EBPSK modulated signals[J]. Chinese Journal of Radio Science, 2008, 23(3): 496-500. (in Chinese)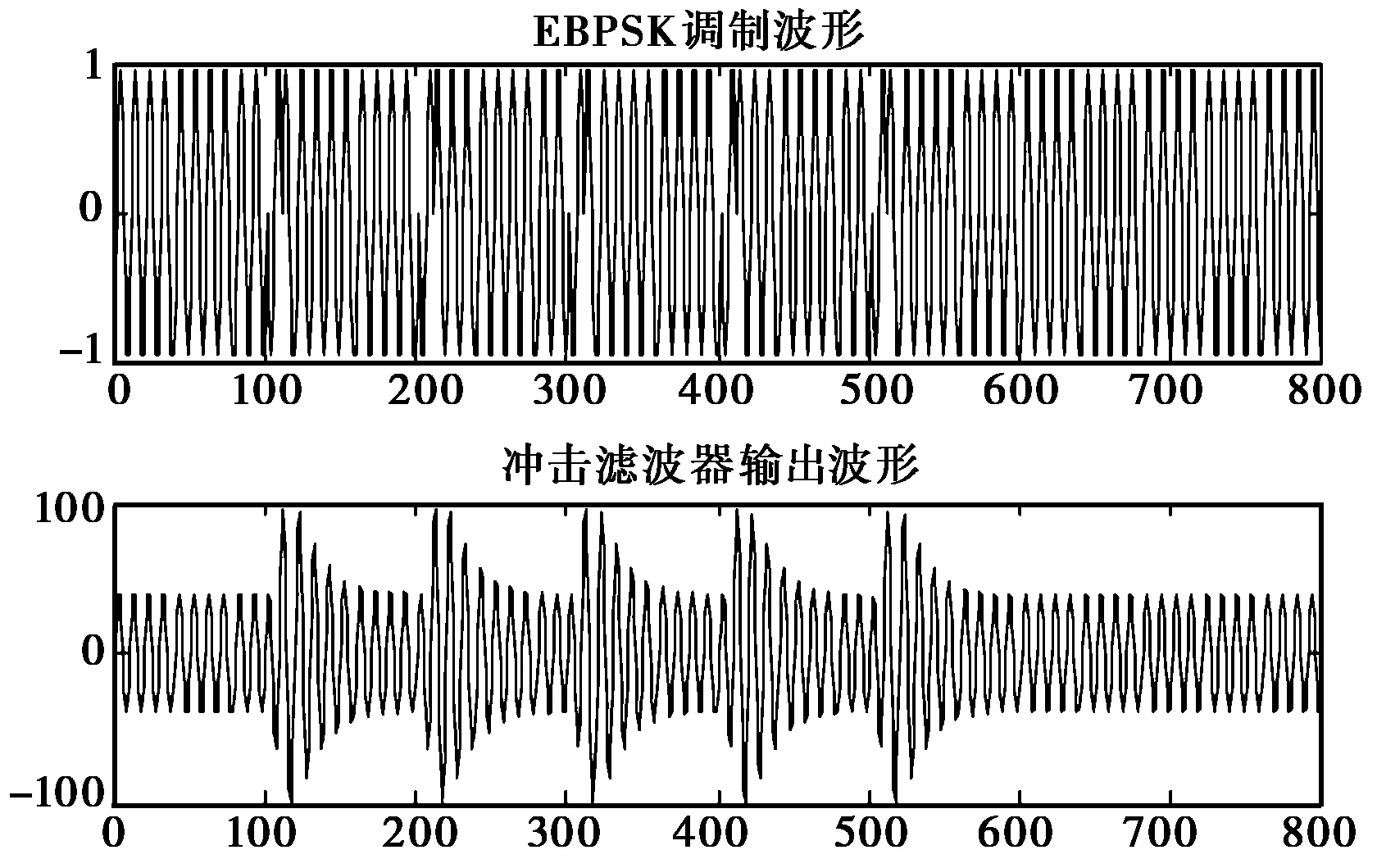
2 功率谱
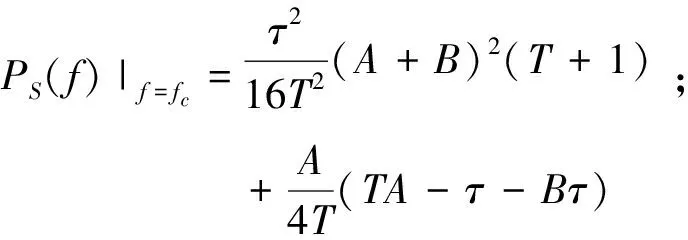
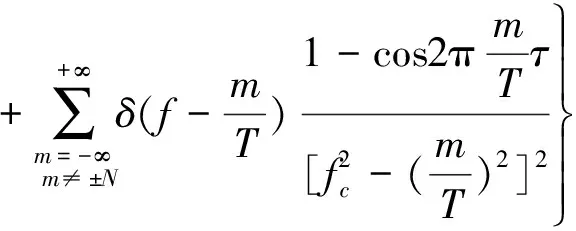
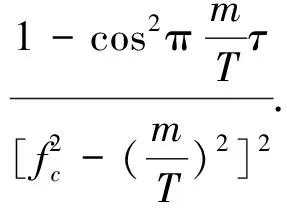
3 发送滤波器
3.1 中心频率的确定
3.2 窗函数的选择



4 中心对称与非中心对称发送滤波器的解调对比
5 结 论

