一种基于Walsh矩阵的正交多相码设计方法

李 军 刘 娜 刘红明 孙 颖 何子述

(电子科技大学电子工程学院，四川 成都 611731)

引 言

正交信号一般应用于多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达体系[1-3]，良好的正交波形能够在空间上形成低增益的宽波束，提高雷达的抗截获性能. 接收信号经过数字多波束技术后，能够形成多个高增益的窄波束，能够同时检测出多个目标.总之，正交波形的设计越来越受到人们的重视.

常见正交波形的信号形式有正交离散频率编码信号[4]、正交频分复用-线性调频信号[5]、正交多相编码信号[6].由于正交多相编码信号带宽利用率高，本文从多相码设计角度对正交波形进行设计.目前正交相位编码信号设计方法多集中在智能领域中，如Liu等[7]利用遗传算法进行正交性的搜索和相关量的优化，但是这种算法很容易陷入局部最优.针对这一现象，Deng[8]利用基于遗传算法的模拟退火算法进行了正交相位编码信号的设计，这一设计虽然具有很强的局部搜索能力，但是却对整个搜索空间不够了解，不利于将搜索过程进入最希望的区域，而且没有解决在目标零偏移点处，信号间严格正交性(后文将在目标零点偏移处信号间严格正交性简称严格正交性)的问题，这将会直接影响到雷达的角度测量精度和杂波对消效果[9-10].为了解决相位编码信号间严格正交性的问题[11]，本文引入了Walsh函数的概念，提出了一种基于Walsh矩阵的正交多相码信号设计方法.Walsh矩阵保证信号间具有严格正交性，通过对Walsh矩阵列变换，为遗传算法提供了严格正交性空间域，使得遗传算法优化速度得到了很大的提升.同时在遗传算法中添加了“和信号”形式的代价函数，使得设计出的信号组在目标检测性能上得到了提升.“和信号”的概念来源于每个接收信号是所有发射信号在空间上叠加后的综合信号，因此对接收的“和信号”做相关处理时，要求所有发射信号都与“和信号”做匹配滤波，各匹配滤波后叠加的综合输出旁瓣量直接决定着雷达对目标的检测性能，根据这一理念才把“和信号”的相关旁瓣输出增加为遗传算法代价函数之一.

本设计方案是在保证信号间严格正交性的同时，尽可能地降低“和信号”相关峰值旁瓣量、自相关峰值旁瓣量以及互相关峰值量.严格正交性的保证是通过变化后的类Walsh矩阵给予的，类Walsh矩阵是通过Walsh矩阵变化重组生成的正交多相码矩阵，Walsh矩阵则是通过Walsh函数采样得到的.低相关旁瓣量则是通过遗传算法对严格正交信号空间域进行筛选实现的.严格正交性使得信号处理时具有更优的角度测量精度和杂波对消效果；低自相关旁瓣量和低互相关量的设计使得发射信号组在空间上能量分布均匀，同时降低了信号间的干扰，便于隐身；低“和信号”相关峰值旁瓣量的设计使得雷达综合输出端有更好的目标检测概率；多相码的设计使得信号更不容易被破获且能够获得比较低的相关旁瓣量.

1 正交多相码信号形式

假设MIMO雷达发射的是一组正交相位编码信号，信号个数为L，每个信号的编码长度为N，那么编码信号集合可表示如下：

{Sl(t)=a(t)ejφl(n),n=1,2,…,N},l=1,2,…,L，

(1)

且为了满足信号间严格正交性，要求任意两个信号间满足关系为

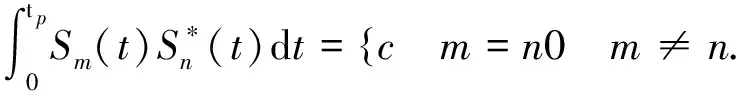
(2)

式中：a(t)为每个码元的载频信号；tp为信号持续时间；φl(n)为第l个信号第n个码元内信号的初始相位，对于四相码来说相位取值为

φl(n)∈{0,π/2,π,3π/2}.

(3)

根据信号的相关处理特性，可以定义自相关A(φl,k)序列、互相关C(φp,φq,k)序列，“和信号”相关S(k)序列表达式为

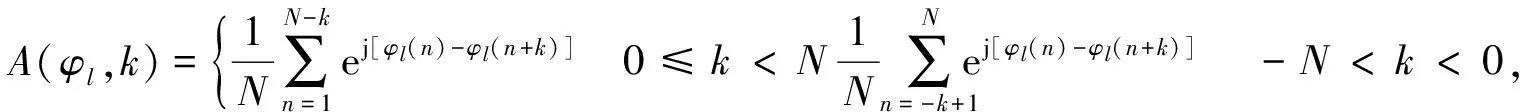
(4)

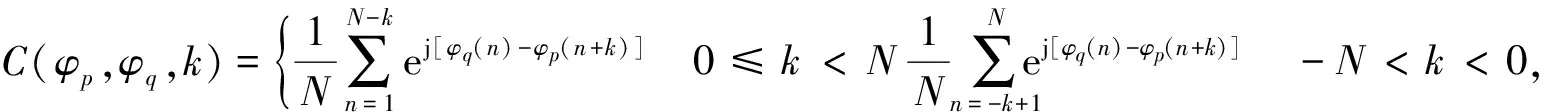
(5)

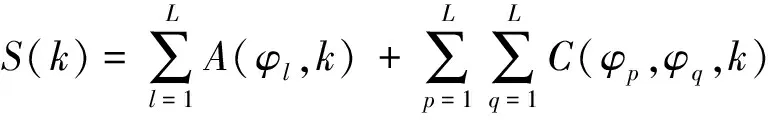
(6)

由于载频信号在每个码元中保持不变，因此在计算相关量时可以不做考虑，简化了计算复杂度.由式(4)、(5)和(6)可见相关输出是一个滑动相关的过程，旁瓣输出是不可避免的.“和信号”相关峰值旁瓣量高将会直接引起虚假目标的产生或者掩盖了真实的弱目标，高的自相关旁瓣量和互相关量则会使得发射信号组在空间上能量分布不均匀，不利于隐身，所以要求设计出的正交相位编码信号具有三种类型的低旁瓣量.

2 基于Walsh矩阵的正交多相码矩阵设计

Walsh矩阵中的每个行向量是通过一组完备的正交函数系Walsh函数等间隔采样得到的，该Walsh函数只有两个取值,分别是+1和-1，假设对N=2v个Walsh函数进行1/N=2-v等间隔采样，那么将会得到一个N×N的Walsh矩阵.Walsh函数正交性数学表述如下：

(7)

例如当v取3时，可以得到如下Walsh矩阵

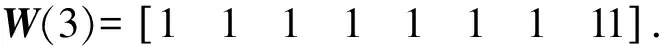
通过采样生成的Walsh矩阵，仅包含两个元素+1和-1，对应到相位上是0和π，满足正交二相码生成逻辑，即满足如下两个逻辑定理：

定理1 多个长度为N的二相码序列彼此正交的必要条件是N为偶数，且取值为+1和-1的子码数相等；

定理2 长度为2m正交二相码序列，可以找到至少包含2m-1个序列构成的正交编码簇，其中任意两个编码之间满足严格正交性约束.

定理证明如下：

定理1的证明：已知二相码编码中每个码元序列的取值只能是+1和-1(分别对应于信号相位0和π)，随机取两个彼此正交的编码序列M1和M2，两个二相编码序列的长度均为N，然后逐个比较两个编码序列的码元，记符号相同的码元个数为N1，符号不同的码元个数为N2，则有N1+N2=N.为保证两个二相码序列严格正交性，N1和N2需满足N1=N2，所以有

N=N1+N2=2N1=2N2.

(8)

由此可见，N必须是偶数才能够保证严格正交性，而且为控制编码序列的自相关旁瓣，二相码序列取+1和-1的数量必须相等，证明完毕.

定理2的证明：利用归纳法，当m=2时定理显然成立，且根据定理1，任意一个二相码序列中+1和-1的个数相等.

假定当m=k0≥2时定理2成立，即存在一个编码长度为N=2k0，含N-1个正交二相码的编码簇，记编码序列为mi，i=1,2,…,N-1.

先构造出三个长度都为2N的二相码簇，第一个记为D，编码总数为N-1，表示为

D={d|di=mi‖mi,i=1,2,…,N-1};

(9)

第二个记为E，编码总数为N-1，表示为

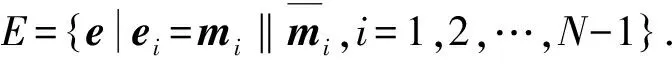
(10)

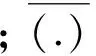
第三个记为F，它只含一个编码序列

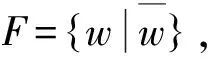
(11)

w为长度为N的全+1二相码串，则并接在一起的为全-1的二相码串.

从簇D和E中各取一个元素di和ej，考察两串二相码之间的正交性，显然有：

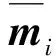
如果i=j，则两串二相码之间符号相同和相反的子码数量各为N，则推出di与ej正交；于是有D与E正交.

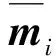
记G为F、D和E三者间的交集，综合前面的推理可知G中所有元素取+1和-1的子码个数相同，并且所有元素两两满足正交的条件，而G中元素的个数为

2(N-1)+1=2(2k0-1)+1=2k0+1-1,

(12)

这说明m=k0+1时定理成立.综合上述过程可知，定理2成立.

通过生成逻辑，Walsh矩阵仅仅满足二相码信号间的严格正交性，并且没有考虑到信号的相关旁瓣输出，需要利用遗传算法对相关旁瓣量进行优化选择以满足实际需求.由于设计出的正交二相码信号相位个数较少，因此需要拓展相位个数，以四相码为例构造出的类Walsh矩阵形式为

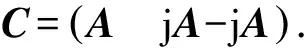
(13)

式中矩阵A为一个N×N的Walsh矩阵，通过A矩阵构造出2N×2N的矩阵C就满足相位个数为四相的正交矩阵，证明如下：

定义ci,cj分别表示为矩阵C的第i,j行，ai,aj分别表示矩阵A的第i,j行.当i,j>N时，则ai=ai-N,aj=aj-N，并且矩阵A中任意两个行向量具有严格正交性，这是由正交Walsh阵的性质决定的，那么C中行向量的取值存在如下两种情况(i,j显然不能取相同的值)：

第一种情况，i,j同时取在前N行或者后N行，那么

ci·cj=ai·aj±j(ai·aj)

=0±j0

=0;

(14)

第二种情况，i,j一个取前N行，一个取在后N行，那么当j=i+N时,

ci·cj

=ai·(-j)aj+jai·aj

=ai·(-j)ai+jai·ai

=-jN+jN

=0,

(15)

当j≠i+N时,

ci·cj

=ai·(-j)aj+jai·aj

=ai·(-j)aj-N+jai·aj-N

=-j0+j0

=0.

(16)

证明完毕.以此类推可以设计出满足8相、16相等类Walsh矩阵，由于Walsh矩阵可以无限制的扩展，因此本文设计出的多相编码信号的编码长度可以无限扩展，但是扩展的编码长度必须为2的正次方倍，原因从二相生成逻辑看，Walsh矩阵可以按照2的次方倍无限扩展，类Walsh矩阵大小与Walsh矩阵存大小存在2倍的关系，因此设计出的正交信号组能够按照2的次方倍无限扩展.

但是，设计出来的类Walsh矩阵从整个生成逻辑上看仅仅是保证了信号间的严格正交性，对于相关旁瓣量依然没有考虑，因此要获得低相关旁瓣量的信号组，需要在类Walsh矩阵形成的严格正交性空间域上，利用遗传算法进行优化选择.类Walsh矩阵形成的严格正交性空间域是指对类Walsh矩阵进行初等列变换后可能形成的各种正交矩阵的集合，由于列变换打乱了原有相位编码的排列顺序，所以通过不同的列变换可以形成不同旁瓣量的正交信号组，根据矩阵理论相关知识了解，列变换不会影响正交矩阵行向量间的严格正交性.

3 遗传算法优化选择

通过重新编排Walsh阵生成类Walsh矩阵，如果直接从其中任意选取某几个行向量作为雷达发射的相位编码信号组，那么信号间具有严格正交性，但是相关旁瓣输出是否比较低却不能保证.并且由于Walsh矩阵生成逻辑的限制，直接抽取其中某几个行向量作为雷达发射信号的编码序列则很容易被破译，从而增大了雷达基站被发现的概率，因此需要通过遗传算法对类Walsh矩阵生成的严格正交性空间域进行优化选择，打乱原有的编码排列逻辑，得到低自相关峰值旁瓣量、低互相关峰值量以及低“和信号”相关峰值旁瓣量的发射信号组.以四相码为例介绍总体设计步骤，流程框图如图1所示.

根据流程框图具体设计步骤如下：

第一步，生成Walsh矩阵A，并按公式(13)编排后生成类Walsh矩阵C作为初始严格正交性空间域的一组值.

第二步，产生初始种群即对设置好大小种群的每个个体的染色体进行编码，每个染色体由两部分组成：一部分编码将译码成正交四相码阵的随机列重排，另一部分编码将译码为对随机列重排后四相码矩阵的随机行抽取.例如需求编码长度为N=4，信号个数L=2的信号组，染色体编码形式如下：

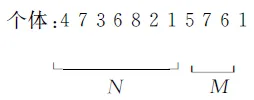
译码表述为：原正交四相码矩阵的第3列、第4列、第1列和第2列重排成为新正交四相码矩阵的第1列、第2列、第3列和第4列，抽取的信号组为新正交四相码矩阵的第2行和第4行.

第三步，适应度值的计算与分配，适应度值的代价函数由自相关峰值旁瓣量、互相关峰值量、“和信号”相关峰值旁瓣量三部分组成，目的在于能够使得发射信号在空间上能量分布均匀，以及提升综合信号对目标的检测性能.

第四步，利用遗传算法中的遗传算子(选择、交叉、变异)对种群进行优化更新.

第五步，重复第三步和第四步直到满足结束条件即遗传代数达到设定的最大值.

图1 流程框图

4 仿真结果

仿真参数设置为编码长度N=1 024，信号个数选择L=4，相位个数选择为四相，最大遗传代数为100.遗传算法优化结束后得到的信号组的归一化相关峰值如表1所示.

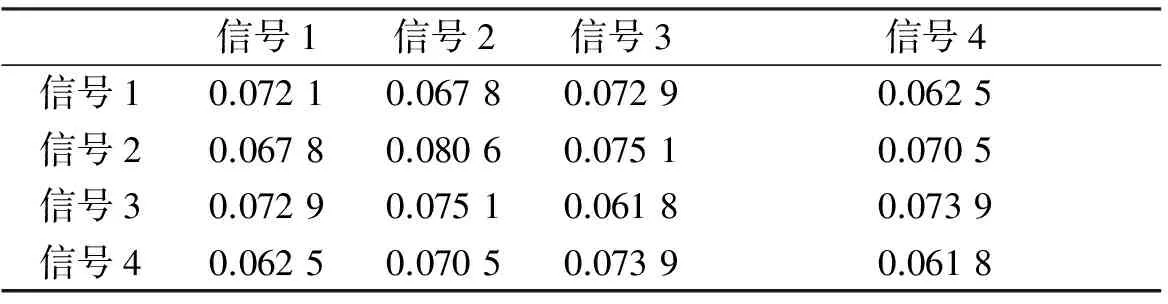
表1 优化后四相码相关峰值表

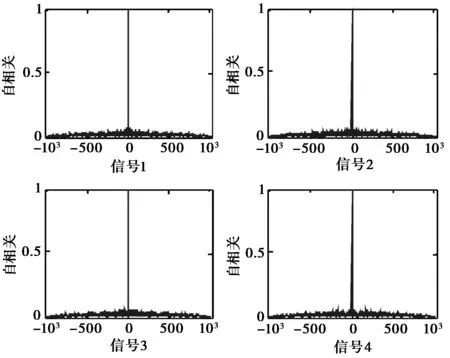
图2 优化后四相码自相关图

图3 优化后四相码互相关图

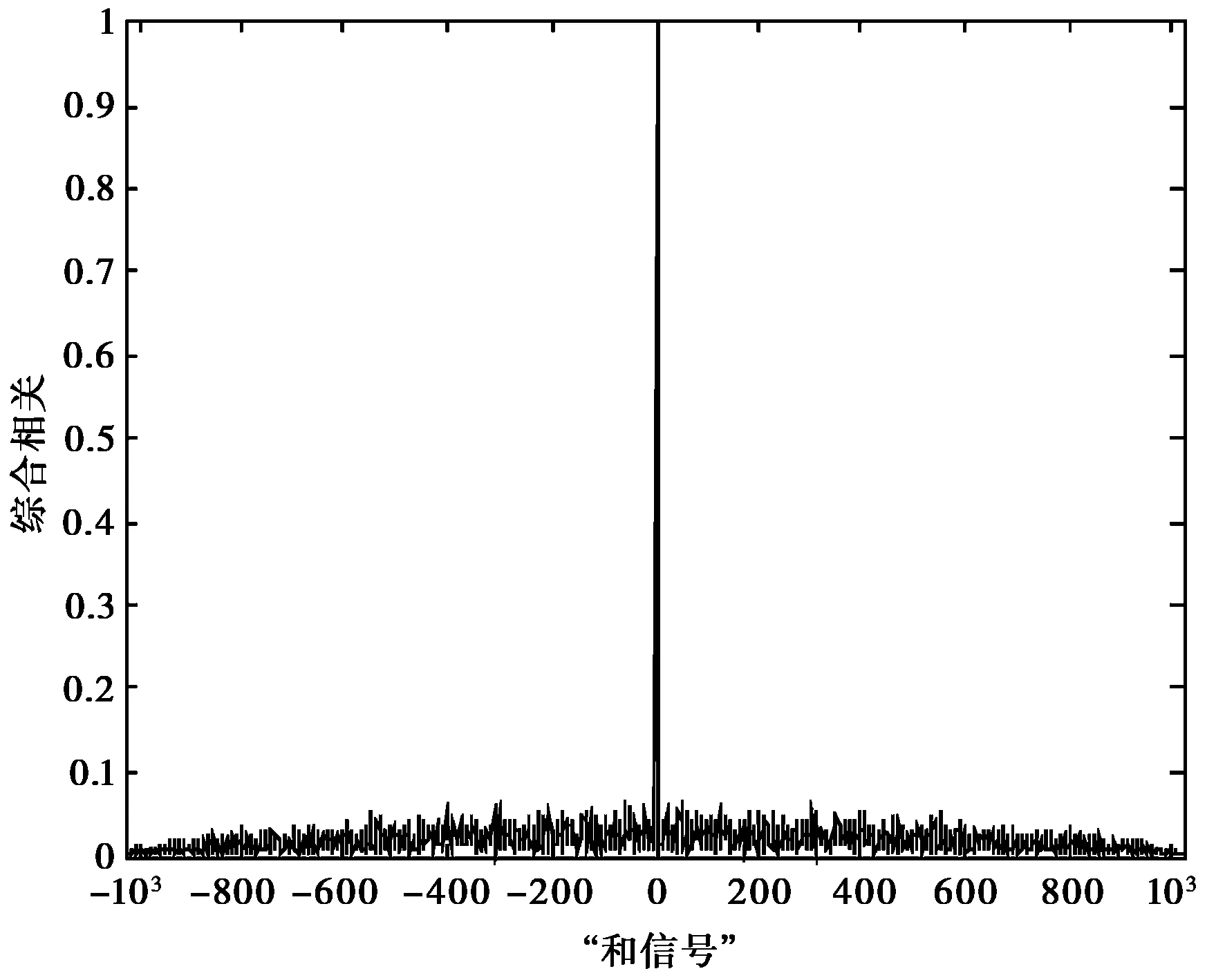
图4 优化后四相码“和信号”相关图

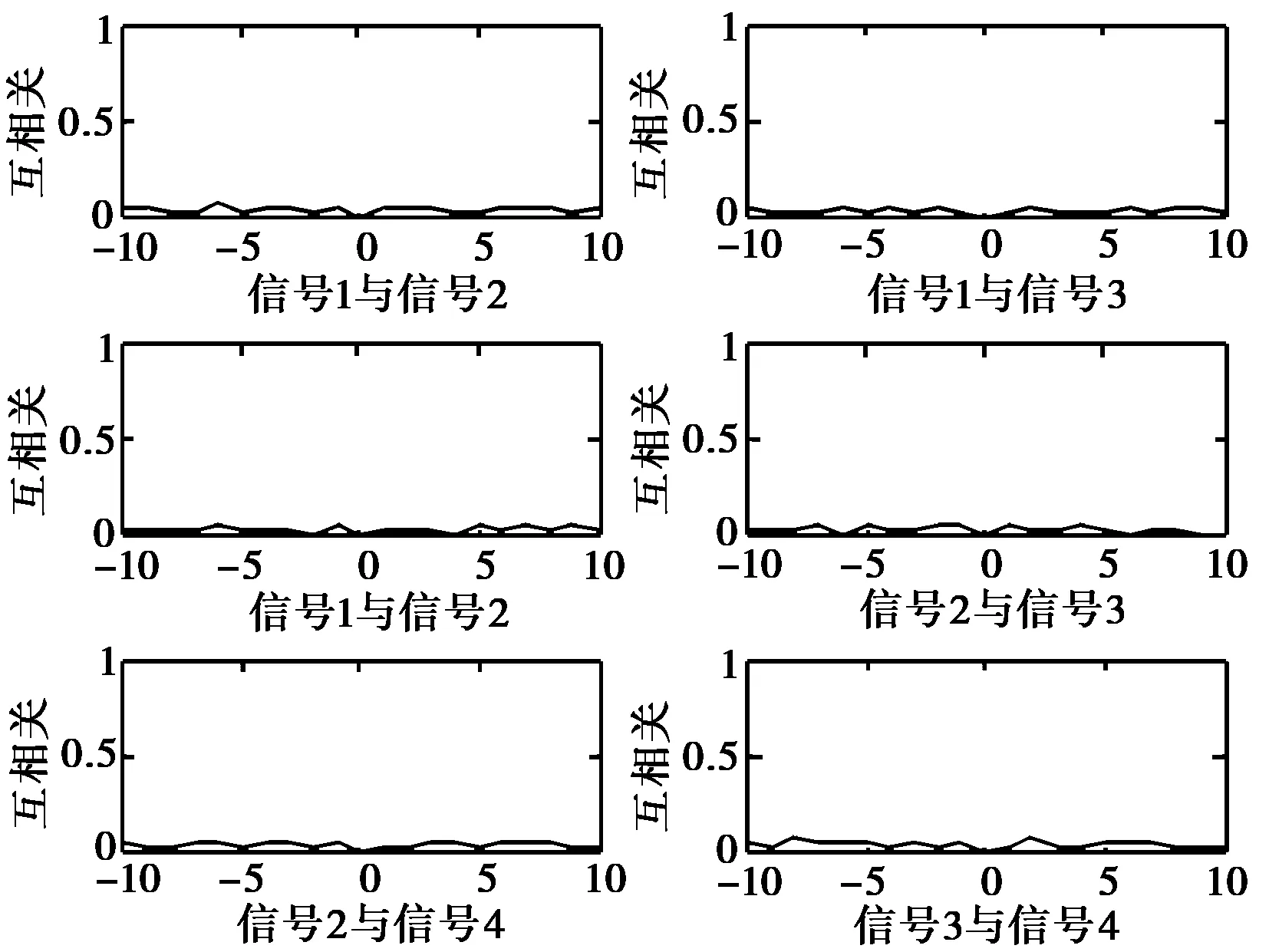
图5 优化后四相码互相关局部图

根据表1得到平均自相关峰值旁瓣量(平均ASP)为0.069 1，平均互相关峰值量(平均CP)为0.070 5即-23.160 3 dB和-23.031 0 dB，“和信号”相关峰值旁瓣为0.061 5(-24.082 4 dB)，所有相关旁瓣量比较低.

设计出的四相码信号的归一化自相关整体图如图2所示；归一化互相关整体图如图3所示；归一化“和信号”相关输出如图4所示.

由图2～4可见“和信号”相关输出旁瓣电平、自相关旁瓣电平和互相关旁瓣电平都是比较低的，使得信号组的抗截获性能更高，同时更容易检测到弱目标并使虚假目标的出现概率降低.

本文的又一个关键点在于设计出的信号组满足严格正交性，通过图5(互相关局部放大图)可以看出信号间在目标零点偏移处互相关量输出为0，说明该方法是可行的.严格正交性的满足，使得信号在角度测量精度和杂波对消效果上得到了很大的提升.

下面针对设计出的正交多相编码信号做多普勒容忍性能分析，设置脉冲重复周期为tr，占空比为η=20%，那么一个脉冲周期内信号持续时间tp=0.2tr.多普勒频率为fd，归一化后的多普勒分辨率(归一化多普勒为fd*tr=fd*5tp)如图6所示.

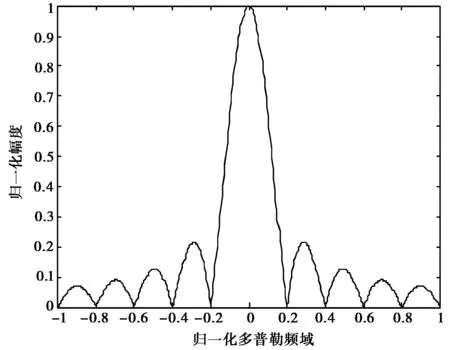
图6 归一化多普勒分辨率

通过图6发现该信号组多普勒分辨率仅与脉冲持续时间有关，与相位编码序列的排列顺序无关，具有一般相位编码信号多普勒容忍性较差的特性，因此相位编码信号一般用于检测静止目标，如果用于探测运动目标，则需要在信号处理端进行多普勒预补偿.

5 结 论

正交相位编码是正交信号的一种重要形式，被广泛的应用于MIMO雷达上.多相码的设计使得雷达信号隐蔽性更强，实际雷达发射相位编码信号需求低综合旁瓣量，从而便于对目标的检测.本文提出了一种正交多相码的设计方法.Walsh函数正交性能的利用使得设计出的多相码序列具有严格正交性，便于提升角度测量精度和杂波对消效果；遗传算法在正交性空间域上优化选择使得信号组具有低旁瓣量，降低了传统遗传算法的优化运算量；增加“和信号”形式的代价函数，使得遗传算法优化出的信号组提升了目标检测性能.

但是，本文设计出来的信号组仍然是相位编码信号，它具有相位编码信号的特有属性，例如对多普勒比较敏感等，这就需要在接收信号处理时，进行多普勒预补偿来解决该问题.

[1] 何子述,韩春林,刘 波.MIMO雷达概念及其技术特点分析[J].电子学报,2005,33(12A):2441-2445.

HE Zishu,HAN Chunlin,LI Bo.MIMO radar and its technical characteristic analysis[J].Chinese Journal of Electronics,2005,33(12A):2441-2445.(in Chinese)

[2] 王 勇,廖桂生,王喜媛.MIMO系统空时特征波束性能分析[J].电波科学学报,2009,24(2):297-301.

WANG Yong,LIAO Guisheng,WANG Xiyuan.Performance analysis of space-time eigen-beamforming in MIMO systems[J].Chinese Journal of Radio Science,2009,4(2):297-301.(in Chinese)

[3] 刘韵佛,刘 峥,谢 荣.一种基于拟牛顿法的MIMO雷达发射方向图综合方法[J].电波科学学报,2008,23(6):1188-1192.

LIU Yunfo,LIU Zheng,XIE Rong.Transmit pattern synthesis algorithm for MIMO radar based on Newton-like method[J].Chinese Journal of Radio Science,2008,23(6):1188-1192.(in Chinese)

[4] 杨 进,邱兆坤,黎 湘,等.一种基于混沌序列的随机离散频率编码信号[J].电子与信息学报,2011,V33(11):2702-2708

YANG Jin,QIU Zhaokun,LI Xiang,et al.Random discrete frequency coding signal based on chaotic series[J].Journal of Electronics & Information Technology,2011,V33(11):2702-2708.(in Chinese)

[5] 刘 波,韩春林,苗江宏.MIMO雷达正交LFM信号设计及性能分析[J].电子科技大学学报,2009,38(1):28-31.

LIU Bo,HAN Chunlin,MIAO Jianghong.OFD-LFM signal design and performance analysis for MIMO radar[J].Journal of University of Electronic Science and Technology of China,2009,38(1):28-31.(in Chinese)

[6] DENG H.Polyphase code design for orthogonal netted radar systems[J].IEEE Trans on Signal Processing,2004,52(11):3126-3135.

[7] LIU Bo,HE Zishu,ZENG Jiankui,et al.Polyphase orthogonal code design for MIMO radar systems[C]// International Conference on Radar.Shanghai,October 16-19,2006,1:113-116.

[8] DENG H.Synthesis of binary sequences with good autocorrelation and cross-correlation properties by simulated annealing[J].IEEE Trans Aerosp Electron Syst,1996,32(1):98-107.

[9] LI J,STOICA P,XU L Z,et al.On parameter identifiability of MIMO radar[J].IEEE Signal Processing Letters,2007,14(12):968-971.

[10] 刘红明,何子述,李 军.双基地MIMO雷达发射阵目标角度估计[J].电波科学学报,2010,25(3):499-504.LIU Hongming,HE Zishu,LI Jun.Transmitter array target angle estimates for bistatic MIMO radar[J].Chinese Journal of Radio Science,2010,25(3):499-504.(in Chinese)

[11] SUN Ying,HE Zishu,LIU Hongming,et al.Binary orthogonal code design for MIMO radar systems[C]// IEEE 2010 international symposium on intelligent signal processing and communication systems.Chengdu,December 6-8,2010.