非均匀线阵多输入多输出雷达成像旁瓣抑方法

王 伟 马跃华 郝燕玲

(哈尔滨工程大学自动化学院，黑龙江 哈尔滨 150001)

引 言

多输入多输出(Multiple Input Multiple Output，MIMO)雷达作为一种新型的雷达体制，受到人们越来越多的关注[1]. MIMO雷达在发射端发射相互正交的信号，再在接收端通过一组匹配滤波器将其分离，形成了远大于实际阵元数的等效阵列[2]，从而给MIMO雷达带来了诸多优势，如更高的角度分辨率[3]、更多的可探测目标数目[4]，以及更灵活的波束方向图设计[5-6]等.

最近很多研究人员致力于非均匀MIMO雷达阵列结构的研究[7-10]. 文献[7-9]研究了最小冗余阵MIMO雷达，通过设计发射阵列和接收阵列结构，使得匹配滤波后形成的MIMO雷达等效阵列为最小冗余阵，利用有限的物理阵元数获得很大的等效阵列孔径长度，从而提高了阵元利用率，改善了空间角度分辨率. 文献[10]将稀疏阵列MIMO雷达用于成像中，由于稀疏阵列的特性，可以获得很高的角度分辨率. 但与此同时，由于非均匀阵列空间采样数的减少，导致波束旁瓣增加，限制了其在目标检测、成像等方面的应用. 如何抑制非均匀线阵MIMO雷达的旁瓣水平，是提高MIMO雷达系统性能的关键.

阵列内插是一种有效的阵列预处理技术，其基本思想是将任意阵列变换成等距均匀线阵[11]，从而可以利用一些为均匀线阵设计的算法，如旋转不变子空间(Estimating Signal Parameters Via Rotational Invariance Techniques，ESPRIT)[12]算法. 文献[13]提出一种基于阵列内插的大间距均匀线阵米波雷达测高方法，有效地克服了波数域变换时存在的角度模糊. 文献[14]将阵列内插技术应用于非均匀线阵MIMO雷达多目标角度估计，虚拟内插后增加了阵元数，从而提高了角度估计性能，增加了可辨识目标数.

本文将阵列内插技术应用于非均匀线阵MIMO雷达成像中，对匹配滤波后形成的等效阵列进行内插变换，将其变换为均匀阵列，并且构造出虚拟均匀阵列的接收信号，在此基础上，采用反向投影(Back Projection，BP)算法[15]进行成像，可以有效地降低旁瓣水平，改善非均匀线阵MIMO雷达的成像性能.

1 MIMO雷达模型

假设MIMO雷达系统含有M个发射阵元，N个接收阵元，采用密集布阵的形式，发射阵列和接收阵列结构如图1所示. 发射阵列和接收阵列都位于x轴上，其法线方向为y轴，左边第一个发射/接收阵元处定义为原点. 假设观测区域包含P个点目标，均满足远场条件，第p个点目标的方位角表示为θp.

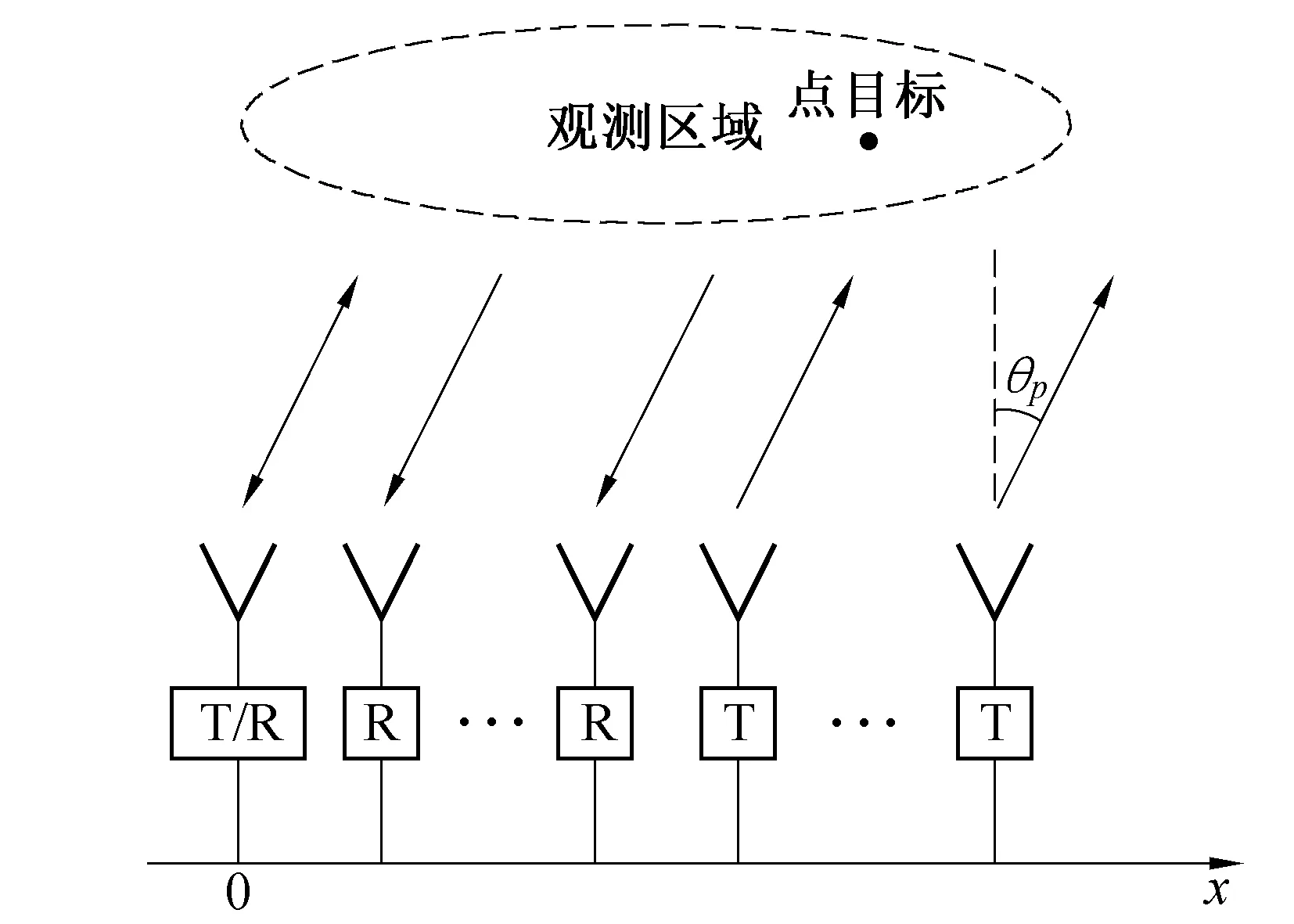
图1 单基地MIMO雷达结构示意图

MIMO雷达各个发射天线发射相互正交的信号，经过目标反射后，接收阵列接收到的信号为

(1)

式中:X∈CN×L为采样后的接收数据，L为采样拍数；βp为第p个点目标的反射系数；S∈CM×L表示发射信号矩阵；W∈CN×L为加性高斯白噪声矩阵；αr(θp)和αt(θp)分别为接收导引矢量和发射导引矢量，具体定义如下：

αr(θp)= [1,exp(-j2πv2sinθp/λ),…,

exp(-j2πvNsinθp/λ)]T,

(2)

αt(θp)= [1,exp(-j2πu2sinθp/λ),…,

exp(-j2πuMsinθp/λ)]T，

(3)

式中，vn表示第n个接收阵元的横坐标，um表示第m个发射阵元的横坐标.

在接收端利用发射信号的正交性对接收信号进行匹配滤波，并堆栈成列可以得到

(4)

式中:c(θi)=αr(θi)⊗αt(θi)定义为MIMO雷达的等效阵列导向矢量，⊗表示克罗内克积运算符；V为匹配滤波后的噪声矩阵. 由式(4)可以看出，MIMO雷达匹配滤波后的信号可以看作是一个等效阵列接收的信号，该等效阵列由发射阵列和接收阵列的空间卷积产生.

非均匀线阵MIMO雷达所采用的发射阵列和接收阵列都为非均匀阵列，空间卷积后得到的等效阵列也为非均匀线阵. 这样的阵列结构具有大的阵列孔径，可以获得更高的空间角度分辨率，但是由于空间的非均匀采样，减少了空间采样数，导致阵列波束旁瓣水平增加，降低了MIMO雷达系统目标检测、成像等的性能. 在下一节中，采用阵列内插技术进行阵列变换，将MIMO雷达等效阵列变换为均匀线阵，并且虚拟出均匀线阵的接收信号，在不增加实际阵元数的情况下提高空间采样率，从而降低旁瓣水平.

2 阵列内插技术

阵列内插技术是一种有效的阵列信号预处理技术，利用阵列内插技术可以将任意阵列变换成一等距均匀线阵或是其他期望的阵列结构，以方便后续的信号处理. 内插阵列变换的基本思想是求出目标区域内的导向矢量，包括原有阵列的导向矢量和期望阵列的导向矢量，再从两个导向矢量中找出变换关系，即求出变换矩阵，从而实现任意阵列到均匀线阵的虚拟变换[11].

假设MIMO雷达观测的目标集中在区域Θ内，经过匹配滤波后得到的等效阵列为非均匀线阵，期望阵列为均匀线阵. 首先对目标区域进行划分，将区域Θ细分为

Θ=[θlθl+Δθθl+2Δθ…θr],

(5)

θl和θr分别为Θ的左右边界，Δθ为步长，则MIMO雷达等效阵列的阵列流型矩阵为

C=[c(θl)c(θl+Δθ) …c(θr)].

(6)

(7)

(8)

从式(8)可以求得以下的变换关系为

(9)

为了获得精确度较高的内插变换矩阵B，可采用小的步长Δθ对观测区域细分. 虽然所需的运算量较大，但对于实际系统来说，这往往是一个离线计算的过程.

得到内插变换矩阵B后，根据式(4)和式(8)，可以求得内插变换后虚拟产生的均匀线阵接收信号为

=BY.

(10)

由式(10)可以看出，利用变换矩阵B和原来MIMO雷达等效阵列的接收信号，可以得到虚拟均匀线阵的接收信号. 比较式(4)和式(10)，空间采样点相当于从原来的MN个变为了uM+vN个，由非均匀阵列的稀疏性可知uM+vN>MN，所以通过阵列预处理的方法得到了原来阵元间隔处的接收信号，在不增加实际阵元的情况下提高了空间采样率，从而降低了旁瓣水平.将MIMO雷达等效阵列内插变换为均匀线阵后还可以利用许多针对均匀线阵设计的算法，如ESPRIT等.

3 成像算法

采用BP算法[15]对MIMO雷达接收信号进行成像处理. BP成像方法适用于任意阵列结构，这样也更便于比较阵列内插前后的成像效果. BP算法的基本思想是首先计算目标点到各个天线孔径点之间的双程时延，而后将相应的时延补偿后进行相干叠加，求叠加结果的幅度得到所需目标的后向散射强度. 对区域进行成像时，先将成像区域划分为一系列网格点，对每个点遍历上述的“延迟求和”过程，即可求出各个点的散射系数，完成对观测区域的成像.

对成像区域进行网格化时采用极坐标形式. 距离向网格与采样时刻一一对应，每一个采样时刻对应一个距离单元，可以理解为匹配滤波并堆栈后所得信号的每一行是一个距离单元的回波信号. 把成像区域在方位向均匀细分为K份，即成像区域所覆盖方位角为[θ1,θ2,…,θK]. 则距离为r，角度为θk处的像素点到MIMO雷达等效阵列的相移矢量可以表示为

a(r,θk)= exp(j4πr/C)[1,exp(j(u1+v2)πsinθk),

…,exp(j(uM+vN)πsinθk)]T.

(11)

式中，C表示电磁波传播速度. 相应的，该像素点到内插变换后形成的虚拟阵列的相移矢量为

exp(j2πsinθk),…,

exp(j(uM+vN)πsinθk)]T.

(12)

式(11)和(12)都具有和阵列导引矢量类似的形式，这与前面设定的远场目标条件是相符的. 考虑某一个距离单元的所有方位角度，可以得到相移矩阵定义如下：

A(r)=[a(θ1),a(θ2),…,a(θK)];

(13)

(14)

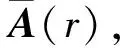
I(r)=Y(r)*AH(r);

(15)

(16)

4 实验仿真与分析

假设MIMO雷达具有4个发射阵元和4个接收阵元，以半波长为标准的坐标分别为(0, 13, 26, 39)和(0, 1, 4, 6). MIMO雷达发射波形采用循环算法[16](Cyclic Algorithm-New, CAN)设计的正交波形，每个发射波形包含码元数为100，载频为10 GHz，带宽设为50 MHz，相应的码元时宽为0.02 μs，脉冲重复周期为6 μs，采样周期等于码元时宽. 考虑二维平面成像，成像区域用极坐标形式描述，以第一个发射(接收)阵元处为原点. 成像区域距离R范围为200～800 m, 方位角范围为-45°～45°，方位角划分网格时步长选为0.1°. 存在单个目标点距离为600 m, 方位角为0°，后向散射系数为1. 进行阵列内插变换区域Θ取为[-10°∶ 0.01°∶ 10°]. 接收阵元处信噪比为30 dB，利用BP成像算法对阵列内插前后的信号进行成像处理，得到的结果如图2所示.

图2中，(a)、(c)表示为未采用阵列内插技术所得成像结果的三维图以及距离R=600 m处的切面图；(b)、(d)为先采用阵列内插预处理再进行成像的结果. 从两组图可以看出：直接利用非均匀的MIMO雷达等效阵列接收信号进行成像处理得到的图像旁瓣较高，这是由于非均匀阵列较稀疏导致的，影响了成像质量. 阵列内插后图像旁瓣明显降低，成像效果显著提高，这是因为虚拟内插相当于补充了阵元间隔处的采样，增加了空间采样率，从而降低了旁瓣水平.

分析不同信噪比对本文所提方法的影响，设置信噪比为[10∶5∶40] dB，以峰值旁瓣比(Peak Side-lobe Ratio，PSLR)作为标准来比较成像效果的好坏. 采用阵列内插和不采用阵列内插成像的峰值旁瓣比如图3所示.

从图3可以看出当信噪比大于20 dB时，采用阵列内插技术后成像结果的PSLR明显降低，这是因为阵列内插技术增加了空间采样率，与此前的理论分析相符. 需要注意的是当信噪比较低时，利用阵列内插后成像结果的PSLR高于未利用阵列内插时，这是因为当信噪比较低时MIMO雷达接收信号中包含噪声分量偏高，导致内插变换误差较大，影响了成像效果. 在MIMO雷达系统中可以采用脉冲积累的方法提高信噪比.

(a) 阵列内插前的成像结果三维图

(b) 阵列内插后的成像结果三维图

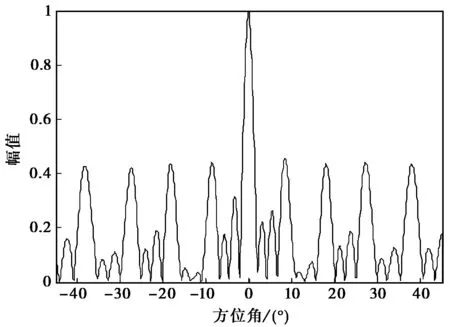
(c) 阵列内插前成像结果的方位向剖面图

(d) 阵列内插后成像结果的方位向剖面图图2 成像结果对比图

图3 信噪比的影响

5 结 论

针对非均匀线阵MIMO雷达空间采样率低，成像旁瓣较高的问题，本文将阵列内插预处理技术应用于MIMO雷达成像，先把非均匀等效阵列内插变换为均匀线阵，再利用标准BP算法进行成像. 仿真实验表明：本文所提方法在信噪比较高时可以有效地降低旁瓣水平，提高成像质量. 另外，所提方法可以将任意阵列结构的MIMO雷达等效阵列变换为均匀线阵，为利用一些基于均匀线阵设计的算法提供了条件.

[1] FISHLER E, HAIMOVICH A, BLUM R, et al.MIMO radar: an idea whose time has come[C]∥ Proc IEEE Radar conf.Pennsylvania, 2004:71-78.

[2] BEKKERMAN I and TABRIKIAN J.Target detection and localization using MIMO radars and sonars [J]. IEEE Trans on Signal Processing, 2006, 54(10): 3873-3883.

[3] BLISS D W, FORSYTHE K W.Multiple-Input Multiple-Output (MIMO) radar and imaging: degrees of freedom and resolution[C]∥ 37th Asilomar Conf on Signals, Systems and Computers. California, 2003: 54-59.

[4] LI J, STOICA P, XU L, and et al.On parameteridentifiability of MIMO radar [J]. IEEE Signal Processing, 2007, 14(12): 968-971.

[5] STOICA P, LI J, XIE Y.On probing signal design for MIMO radar [J]. IEEE Trans on Signal Processing, 2007, 55(8): 4151-4161.

[6] 刘韵佛, 刘 峥, 谢 荣.一种基于拟牛顿法的发射方向图综合方法[J].电波科学学报, 2008, 23(6): 1188-1193.

LIUYunfo, LIU Zheng, XIE Rong.Transmit pattern synthesis algorithm for MIMO radar based on Newton-like method [J].Chinese Journal of Radio Science, 2008, 23(6): 1188-1193.(in Chinese)

[7] CHEN C, VAIDYANATHAN P P.Minimum redundancy MIMO radars [C]∥ Proc ISCAS.Washington, 2008: 45-48.

[8] 王 伟, 马跃华, 王咸鹏.低冗余度多输入多输出雷达阵列结构设计[J].电波科学学报, 2012, 27(5): 968-972.

WANG Wei, MA Yuehua, WANG Xianpeng.Low-redundancy MIMO radar array structure design[J].Chinese Journal of Radio Science, 2012, 27(5): 968-972.(in Chinese)

[9] 张 娟, 张林让, 刘 楠.阵元利用率最高的MIMO雷达阵列结构优化算法[J].西安电子科技大学学报, 2010, 37(1): 86-90.

ZHANG Juan, ZHANG Linrang, LIU Nan.Array optimization algorithm for MIMO radar with a maximum physical sensors efficiency[J].Journal of XIDIAN University, 2010, 37(1):86-90.(in Chinese)

[10] SCHINDLER J K.Sparse, active aperture imaging [J].IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 202-209.

[11] GERSHMAN B A, BOHME F J.A note on most favorable array geometries for DOA estimation and array interpolation [J].IEEE Signal Processing Letters, 1997, 4(8): 232-235.

[12] KASSIS E, PICHERAL J, MOKBEL C.EM-Esprit algorithm for direction finding with nonuniform arrays[C]∥ IEEE 14th workshop on statistical signal processing.Madison, 2007, 453-457.

[13] 胡铁军, 杨雪亚, 陈伯孝.阵列内插的波束域ML米波雷达测高方法[J].电波科学学报, 2009, 24(4): 660-666.

HU Tiejun, YANG Xueya, CHEN Boxiao.Application of beamspace ML algorithm based on array interpolation in height measuring using VHF radar [J].Chinese Journal of Radio Science, 2009, 24(4): 660-666.(in Chinese)

[14] 王 伟, 王咸鹏, 李 欣.非均匀线阵MIMO雷达的多目标定位方法[J].系统工程与电子技术, 2012, 34(3): 477-481.

WANG Wei, WANG Xianpeng, LI Xin.Multi-target localization for non-uniform linear array of MIMO radar[J].Systems Engineering and Electronics, 2012, 34(3): 477-481.(in Chinese)

[15] 王怀军, 黄春琳, 陆 珉, 等.MIMO雷达反向投影成像算法[J].系统工程与电子技术, 2010, 32(8): 1567-1573.

WANG Huaijun, HUANG Chunlin, LU Min, et al.Back projection imaging algorithm for MIMO radar [J].Systems Engineering and Electronics, 2010, 32(8): 1567-1573.(in Chinese)

[16] HE H, STOICA P, LI J.Designingunimodular sequence sets with good correlations-including an application to MIMO radar[J].IEEE Transactions on Signal Processing, 2009, 57(11): 4391-4405.