基于自适应频率选择的OTHR多模传播抑制研究

李铁成 李 雪 冯 静 鲁转侠

(中国电波传播研究所，山东 青岛 266107)

引 言

天波超视距雷达(Over-the-Horizon Radar，OTHR)利用电离层折射、返回散射传播机理来实现超视距覆盖，克服了地球曲率限制，作用距离达1 000～4 000 km，覆盖范围几百万平方千米[1-2]，对敌方飞机、舰船和导弹目标等具有早期预警的突出优点[3-4].电离层是OTHR的主要传播媒介，具有时变、随机、色散和各向异性等特性，影响雷达信号传播，特别是电离层相位污染和多模传播引起OTHR地海杂波频谱大幅度展宽，使得OTHR对舰船目标的检测能力急剧下降[5-7].

电离层相位污染的本质是电离层的非平稳特性使得通过电离层传播的射线相位路径发生变化，导致回波信号相位非相干，引起OTHR地、海杂波频谱大幅展宽，制约舰船等低速目标检测.目前关于电离层相位污染抑制算法较多，主要分为两大类：一是采用短相干积累时间(Coherebt Integration Time,CIT)来避免电离层的非平稳性；二是目前OTHR中广泛应用的时域估计补偿方法，比较流行的算法有最大熵谱估计法[8]、相位梯度估计法[9]、时频分析法[10]和特征分解法[11]等.文献[12]采用分段多项式相位信号(Polynomial Phase Signal,PPS)建立电离层相位调制函数模型，并利用高阶模糊函数(High-order Ambiguity Function,HAF)法分析每段的瞬时相位，最后综合出整段校正函数.文献[13]给出了几种快速判断多项式相位信号阶数的方法，进一步提升了该方法的工程适用性.

电离层多模传播本质是其分层特性使得不同地面距离回波落入同一群距离单元，引起地、海杂波谱大幅展宽，扩大检测盲速区，限制海面慢速目标检测.文献[14]提出了基于二维天线阵列的多模传播抑制算法，该方法利用二维数字波束形成技术实现俯仰、方位上窄波束探测，使得雷达系统工作于单一传播模式.由于要求俯仰和方位分辨率较高，造价昂贵.目前法国的NOSTRADAMUS天波超视距雷达系统采用二维星型天线阵列，这种方法利用高硬件配置提升系统能力，思路简单清晰，问题解决最为彻底.文献[15]提出了基于多模-单模转换的方法.该方法受传播模式数目、各模式信号幅度、多普勒频移等估计误差影响较大；文献[16]提出了海杂波循环对消法抑制天波超视距雷达多模传播.该方法不将多模转化为单模，而是直接在多模条件下利用海杂波循环对消去除多个Bragg峰，从而发现目标.但该方法受各模式信号幅度、多普勒频率、初相等估计精度影响，通常需要多次对消以应对杂波剩余.文献[17]提出依据天波超视距雷达配置的电波环境探测系统，利用自适应频率选择实现多模传播抑制，但文献中未提及具体实现方法.

目前，电离层相位污染和多模传播均亟待解决，但又以多模传播抑制最为棘手.

上述提及的多模传播抑制方法中以基于频率选择的方法抑制多模式传播最为实际、有效，即使有时由于对探测目标覆盖及环境干扰等原因不存在单模工作频率，但若能选择传播模式较少的工作频率，也将降低后续采用基于信号处理技术的多模抑制难度.

本文提出了一种基于特征分解的返回散射定频探测不同距离单元传播模式数目提取算法，实现了基于定频探测的全频段传播模式数目分布智能提取，从而最终实现针对某一指定探测区域的单模式工作频率选择.

1 基于返回散射定频探测的单模工作频率选择

1.1 电离层返回散射定频探测

返回散射探测是OTHR重要的电波环境监测手段.其工作原理是其发射信号斜投射到电离层，经折射后照射到地面或海面，地海杂波散射的信号有一部分将沿着原路径再次经电离层折射回到发射点，被那里的接收机接收，如图1所示.

图1 返回散射探测原理示意图

返回散射探测包括扫频探测和定频探测两种.返回散射扫频探测是指探测设备在较短时间内按照一定频率列表迅速完成整个频段的扫描，得到返回散射扫频电离图.返回散射定频探测是指，在某一频点上驻留多个探测脉冲，利用相干积累技术获得多普勒频谱，由于单频点工作时间较长，因此覆盖全频段工作是探测频点不宜选择过多，以免探测周期过长.

显然，返回散射定频探测方式与雷达系统工作方式完全相同.因此，若能获取单频点定频探测传播模式数目随探测距离的分布，并设置定频探测频点已一定的频率步进覆盖全频段，则可获得先验的雷达系统探测全频段内传播模式数目随工作频率和探测距离的分布，从而实现基于频率选择的多模传播抑制.

图2为仿真的电离层传播模式数目随频率和探测距离的分布图.显然，从该图中可直接获得某一探测距离上的单模工作频段.

图2 返回散射定频探测传播模式提取结果示意图

1.2 基于返回散射定频探测的单模工作频率选择流程

基于返回散射定频探测的单模工作频率选择具体步骤如下：

1) 进行返回散射定频探测频率选择；

2) 根据选择的定频探测频率集进行返回散射定频探测；

3) 采用特征分解法提取单频点传播模式数目分布；

4) 综合各频点传播模式数目分布提取结果，获得全频段传播模式数目分布；

5) 根据指定探测距离，获取单模工作频段.

图3给出了基于返回散射定频探测的OTHR单模工作频率选择流程.

图3 基于返回散射定频探测的OTHR单模工作频率选择流程

1.3 返回散射全频段定频探测频率选择原则

返回散射全频段定频探测频率选择需满足以下基本原则：

1) 选择的定频探测频率下限为覆盖雷达最低探测频率，上限为当前电离层允许的最高可用频率；

2) 选择的定频探测频率应为干净频点，即不受电台等外界干扰，且噪声基底应尽可能的低；

3) 选择的定频探测频率间隔应不大于1 MHz，满足对全频段传播模式分布的采样要求.

1.4 基于特征分解的返回散射单频点定频探测传播模式数目分布获取

1.4.1 特征值和特征向量

特征分解(Eigende composition)，又称谱分解(Spectral decomposition)，可将矩阵分解为其特征值和特征向量之积.

设矩阵A为N×N的矩阵，ν为N维非零向量，若

Aν=λν.

(1)

则称λ为矩阵A的特征值，ν为特征值λ对应的特征向量.由式(1)可得

p(λ)=det(A-λI)=0 ,

(2)

式中p(λ)为矩阵的特征多项式，式(2)也称为矩阵的特征方程.特征多项式是关于未知数λ的N次多项式.由代数基本定理，特征方程有N个解.这些解的解集也就是特征值的集合，有时也称为“谱”(Spectrum).

对特征多项式p(λ)进行因式分解，可得：

p(λ)=(λ-λ1)n1…(λ-λk)nk=0.

(3)

其中

(4)

对每一个特征值λi，有下式成立：

(A-λiI)=0.

(5)

对每一个特征方程，都会有mi(1≤mi≤ni)个线性无关的解.这mi个向量与一个特征值λi相对应.这里，整数mi称为特征值λi的几何重数，而ni称为代数重数.这里需要注意的是几何重数与代数重数可以相等，但也可以不相等.一种最简单的情况是mi=ni=1.特征向量的极大线性无关向量组中向量的个数可以由所有特征值的几何重数之和来确定.

1.4.2 矩阵的特征分解

令qi(i=1,…,N)为矩阵A的N个线性无关的特征向量.这样，A可以被分解为

A=QΛQ-1.

(6)

式中：Q是N×N方阵，且其第i列为A的特征向量qi;Λ是对角矩阵，其对角线上的元素为对应的特征值，也即Λii=λi.

一般来说，特征向量qi(i=1,…,N)一般被正交单位化(这不是必须的).未被正交单位化的特征向量组νi(i=1,…,N),也可以作为Q的列向量，可以理解为Q中向量的长度都被Q-1抵消了.

1.4.3 基于特征分解的返回散射定频探测传播模式数目提取

假设OTHR回波信号不存在相位污染，来自K个相邻距离、方位单元的回波信号传播模式数目相同.其中第k个距离、方位单元上的回波序列表示为

(N-1)TR)]

(7)

式中：k=1,2,…,K；TR为脉冲重复周期；N为一个CIT内脉冲重复周期的个数.

用K个回波序列分别构成数据矩阵X的每一列，如式(8)所示：

X=

(8)

矩阵X的维数是N×K，其协方差矩阵为

R=XXH/K

(9)

对协方差矩阵R进行特征分解，将其特征值按大小排列为λ1>λ2>…>λp，并划分信号子空间Us和噪声子空间Un.由于协方差矩阵中杂波能量占主要部分，且比目标信号和噪声高出很多，因此特征值λi中存在若干个(设为r)明显大的特征值，其对应的特征矢量S1,S2,…,Sr所张成的空间即为杂波子空间Us，而余下的p-r个特征矢量G1,G2,…,Gp-r所张成的空间为噪声子空间Un.这里杂波对应的特征值个数r根据特征值的数值范围自动判别，考虑一阶海杂波正负峰成对出现，传播模式数目为r/2.

图4为仿真的返回散射定频电离图，工作频率为15 MHz，其中地、海杂波回波利用正弦信号模拟，由于本文只关注传播模式数目，因此仿真图形中未考虑回波能量随距离、传播模式的变化.仿真中，各距离段预设的传播模式数目如表1所示.

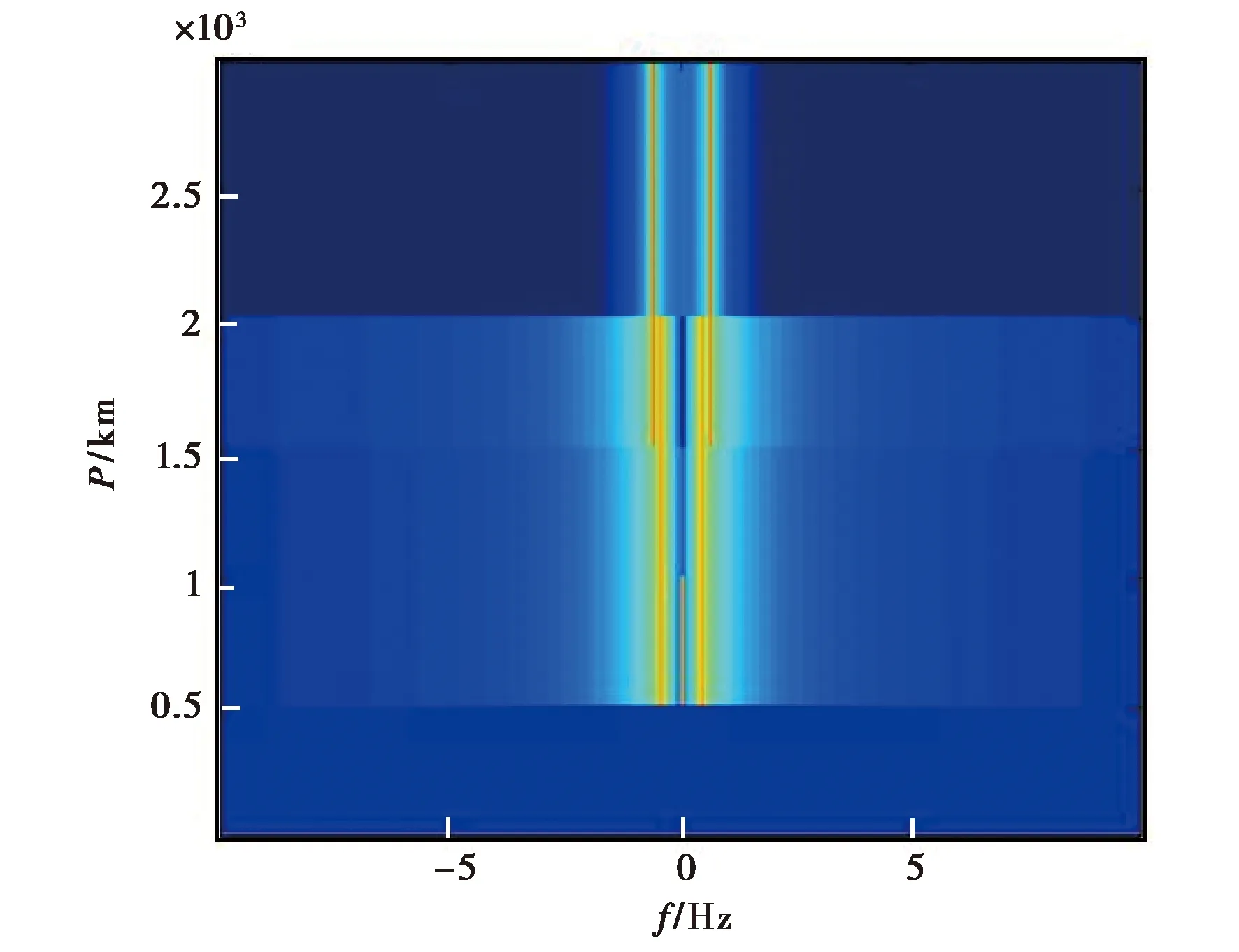
图4 仿真的返回散射定频探测电离图

采用上述基于特征分解的传播模式数目获取方法对图4所示数据进行处理，获得了各距离门传播模式数目，如表1 所示.提取结果与预设结果吻合.

从分析结果中不难看出，若雷达关注的探测距离段为1 500～2 000 km，该频点存在两个传播模式，不利于进行舰船等低速目标探测.若关注的探测距离段为2 000～3 000 km，则该频点为单模传播.

表1 不同距离段传播模式数目分布

1.5 全频段传播模式数目分布获取

利用基于特征分解的传播模式数目提取算法对所有定频探测频点进行分析，即可获得全频段传播模式数目随探测距离的分布.

1.6 单模传播频段确定

获得全频段传播模式数目随距离分布后，根据指定探测距离段，即可直接确定单模工作频段，实现OTHR多模传播抑制.

2 试验验证

正如前面所指出，自适应频率选择实现多模传播抑制的核心是基于特征分解的单频点传播模式数目分布提取算法.本文主要针对这一算法进行试验数据验证.

图5为2012年5月16日某电离层返回散射探测站测得的返回散射定频探测电离图.该返回散射探测仪收发分置，相距约100 km.采用线性调频脉冲工作方式，工作频率14.723 MHz脉冲宽度6 ms，调频带宽10 kHz，脉冲重复周期50 ms，相干积累次数512，相干积累时间25.6 s，采样率80 kHz，探测频率范围5～28 MHz.图6为工作频率16.547 MHz对应的返回散射定频探测电离图，与图5探测时间相差25.6 s.

采用基于特征分解的传播模式数目获取方法对图5、6所示数据进行处理，获得了各距离门传播模式数目，如表2、3所示.

图5 返回散射定频探测结果(14.723 MHz)

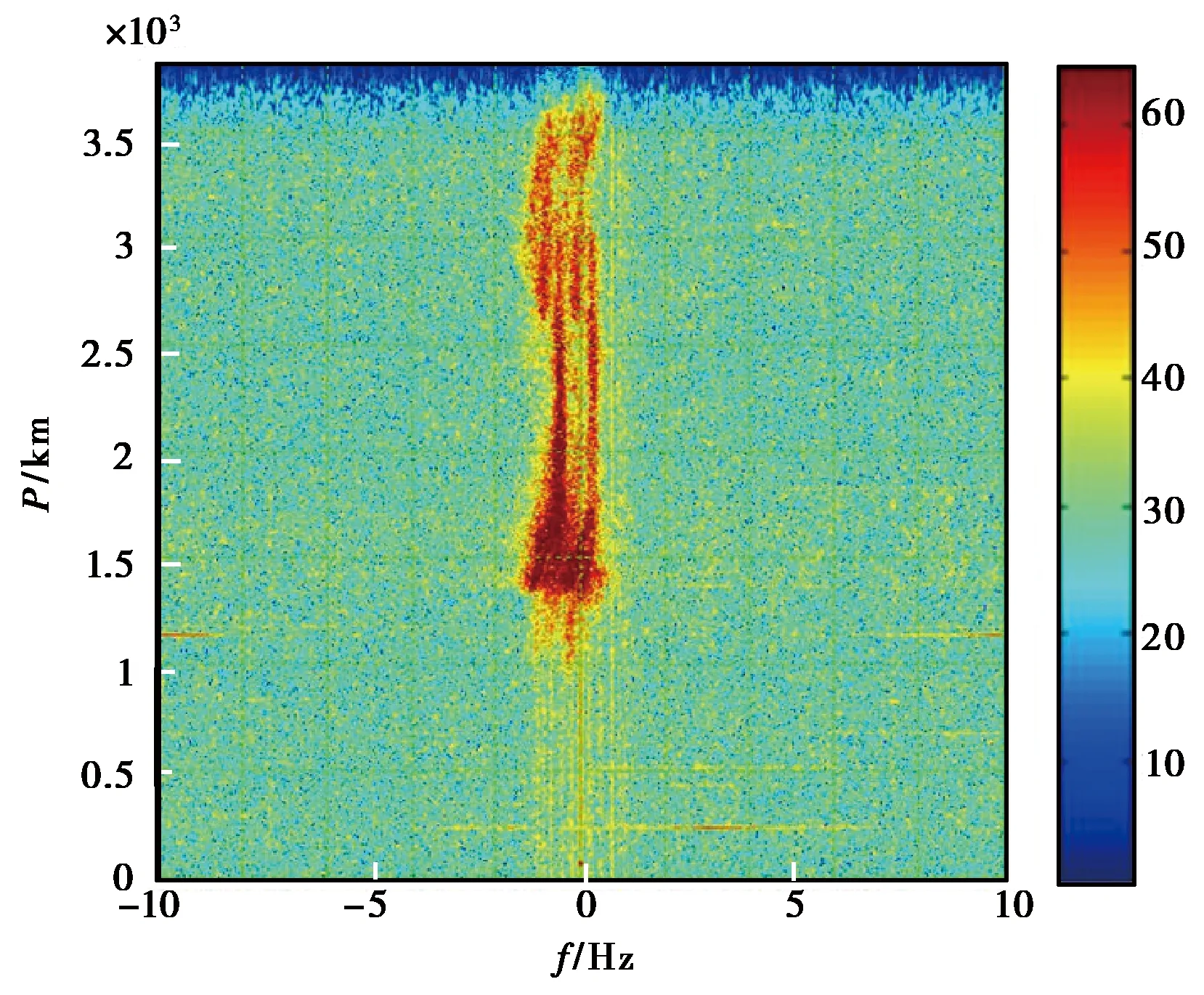
图6 返回散射定频探测结果(16.547 MHz)

序号距离段传播模式数目11300～2000km222000～2580km132580～3500km3

表3 不同距离段传播模式数目分布

显然，若雷达系统关注的探测距离段为2 000～2 500 km，则上述两个频点均满足单模式探测要求.若雷达系统关注的探测距离段为2 500～3 000 km，则需采用频率16.547 MHz进行探测，频率14.723 MHz不满足单模探测要求.

3 结 论

返回散射定频探测工作原理、探测体制、传播路径等与OTHR完全相同.采用特征分解技术对全频段返回散射定频探测结果进行处理可获得OTHR全频段内传播模式数目随距离分布，以此作为先验信息可实现基于工作频率选择的多模传播抑制.该问题的成功解决，将大幅提升OTHR对海面舰船目标检测能力.

[1] NELASON R, MILLMAN G H. HF sky-wave backscatter radar for over-the-horizon ditection[C]// Collected Papers on Over-the-Horizon Radar, 2001: 151-154.

[2] HEADRICK J M. Looking over the horizon[J]. IEEE Spectrum, 1990, 27(7): 36-39.

[3] MARTORELLA M, SOLETI R, BERIZZI F, et al. Plume effect on radar cross section of missiles at HF band[C]// Proceedings of the International Conference Radar, 2003: 656-661.

[4] STAUSBERGER D J, GARBER E D, Chamberlain N F, et al. Modeling and performance of HF/OTH radar target classification systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(2): 396-403.

[5] 凡俊梅, 焦培南, 肖景明. 海洋杂波对高频雷达检测海面上低速目标的影响[J]. 电波科学学报, 1997, 12(2): 205-210.

FAN Junmei, JIAO Peinan, XIAO Jingming. The sea clutter effect on the low Doppler targets detection by HF radar[J]. Chinese Journal of Radio Science, 1997, 12(2): 205-210. (in Chinese)

[6] 郭 欣, 倪晋麟, 刘国岁. 短相干积累条件下天波超视距雷达的舰船检测[J]. 电子与信息学报, 2004, 26(4): 613-618.

GUO Xin, NI Jinlin, LIU Guosui. The ship detection of sky wave over-the-horizon radar with short coherent integration time[J]．Journal of Electronics & Information Techoonology, 2004, 26(4): 613-618. (in Chinese)

[7] 黄德耀. 高频雷达海洋回波谱特性及影响其质量的因素[J]. 电波科学学报, 1996, 11(2): 94-101.

HUANG Deyao. Character of HF radar sea echo spectra and factor of the effects on the quality of the spectra[J]. Chinese Journal of Radio Science, 1996, 11(2): 94-101. (in Chinese)

[8] BOURDILLON A, GAUTHIER F, PARENT J. Use of maximum entropy spectral analysis to improve ship detection by over-the-horizon radar[J]. Radio Science, 1987, 22(2): 313-320.

[9] 邢孟道, 保 铮. 电离层电波传播相位污染校正[J].电波科学学报, 2002, 17(2): 129-133.

XING Mengdao, BAO Zheng. Phase perturbation correction in ionospheric electromagnetic wave propagation[J]. Chinese Journal of Radio Science, 2002, 17(2): 129-133. (in Chinese)

[10] HOWLAND P E, COOPER D C. Use of the Wigner-Ville distribution to compensate for ionospheric layer movement in high-frequency sky-wave radar systems[J]. IEEE Proceedings-F, 1993, 140(1): 29-36.

[11] ANDERSON S J, ABRAMOVICH Y I. A Unified approach to detection, classification, and correction of ionospheric distortion in HF sky wave radar systems[J]. Radio Science, 1998, 33(4): 1055-1067.

[12] LU Kun, WANG Jiong, LIU Xingzhao. A piecewise parametric method based on polynomial phase model to compensate ionospheric phase contamination[C]//Pro of ICASSP. Hong Kong, 2003: 405-409.

[13] 李 雪, 邓维波, 焦培南. 分段多项式建模解电离层慢径相位污染阶数选择新方法[J]. 电波科学学报, 2009, 24(6): 1-6.

LI Xue, DENG Weibo, JIAO Peinan. Novel order-select method of polynomial modeling for ionosphere phase perturbation correction[J]. Chinese Journal of Radio Science, 2009, 24(6): 1-6.(in Chinese)

[14] BAZIN V, MOLINIE J P, MUNOZ J. A general presentation about the OTH-radar NOSTRADAMUS[C]// IEEE Conference on Radar, 2006, 17(8): 634-642.

[15] 杨志群. 天波超视距雷达信号处理方法研究[D].南京: 南京理工大学, 2003.

YANG Zhiqun. Research on Signal Processing of Sky-wave Over-the-Horizon Radar[D]. Nanjing: Nanjing University of Scienee and Technology, 2003. (in Chinese)

[16] 郭 欣. 天波超视距雷达信号处理技术研究[D]. 南京: 南京理工大学, 2004.

GUO Xin. Study on Skywave Over-the-Horizon Radar Signal Proeessing[D]. Nanjing: Nanjing University of Scienee and Technology, 2004. (in Chinese)

[17] ANDERSON S J, MEI F J, JIAO P N. Enhanced OTHR ship detection via dual frequency operation[C]// Proceedings of 2001 CIE International Conference on Radar, 2001: 85-89.