矩量法精确求解磁场积分方程的有效方法

吴君辉 曹祥玉 袁浩波 高 军

(1.空军工程大学信息与导航学院,陕西 西安 710077；2.西安电子科技大学 天线与微波技术国防重点实验室,陕西 西安 710071)

引 言

矩量法[1]是数值计算积分方程的经典算法，得到了国内外众多学者的认同和深入研究. 特别是1982年RWG(Rao-Wilton-Glisson)三角形网格函数的提出，将其作为矩量法求解理想导体电场积分方程(Electric Field Integral Equation,EFIE)的基函数和权函数[2]，使矩量法成为求解目标电磁特性的主要方法. EFIE计算结果精确，是电磁数值计算的最常用公式[3]，但它存在迭代求解难以收敛的问题. 磁场积分方程(Magnetic Field Integral Equation，MFIE)具有较好的迭代收敛性，但在前人的研究中发现它的计算精度远不及EFIE，通常只在混合场积分方程(Combined Field Integral Equation，CFIE)中出现，用于改善EFIE的收敛性. 但CFIE的未知量翻倍，计算电大目标将增加巨大的计算量. 若MFIE可以取得良好的精度，单独采用其求解电大目标，不失为一种优秀的方法. 为了提高MFIE的精度，文献[4]给出了MFIE近奇异性的处理方法，但并不能完全解决问题. 文献[5]分析了MFIE精度低的原因，文献[6]对立体角进行了修正，文献[7]指出MFIE中隐含弱奇异性.

特别分析了MFIE隐含的外层积分弱奇异性，在不对积分方程做额外修正的情况下，仅通过简单有效的积分变换消除了MFIE的奇异性，使矩量法求解MFIE可以获得良好的精度，准确地计算目标雷达散射截面(Radar Cross Section ，RCS)，为以后开发基于MFIE的快速算法求解电大目标问题打下基础.

1 基于RWG函数的MFIE

矩量法计算的一个关键因素是基函数的选取. 由于三角形网格具有良好的描述复杂外形的能力，并且RWG函数满足电流连续性的性质，采用RWG基函数求解EFIE得到了广泛的研究与应用[2]，并解决了EFIE求解中1/R项奇异性的问题[8]. 因此对MFIE进行矩量法求解仍采用RWG基函数并使用伽略金法，RWG基函数表达为[9]

(1)

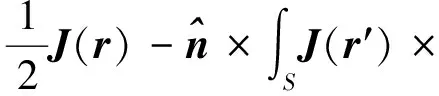
(2)

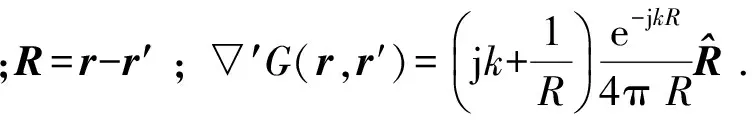
ZmnIn=Vm.

(3)

式中:

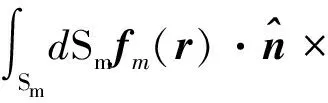
由于与权函数作内积，Zmn具有内外两层积分. 内层积分中的 ▽′G(r,r′)可提取出 1/R2强奇异点，使它的奇异性处理比EFIE更加复杂.

2 MFIE奇异性的消除

2.1 内层积分中的奇异性处理

首先将Zmn中奇异点所在的内层积分提出并带入基函数展开单独分析[5],有

(4)

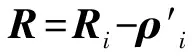
(5)

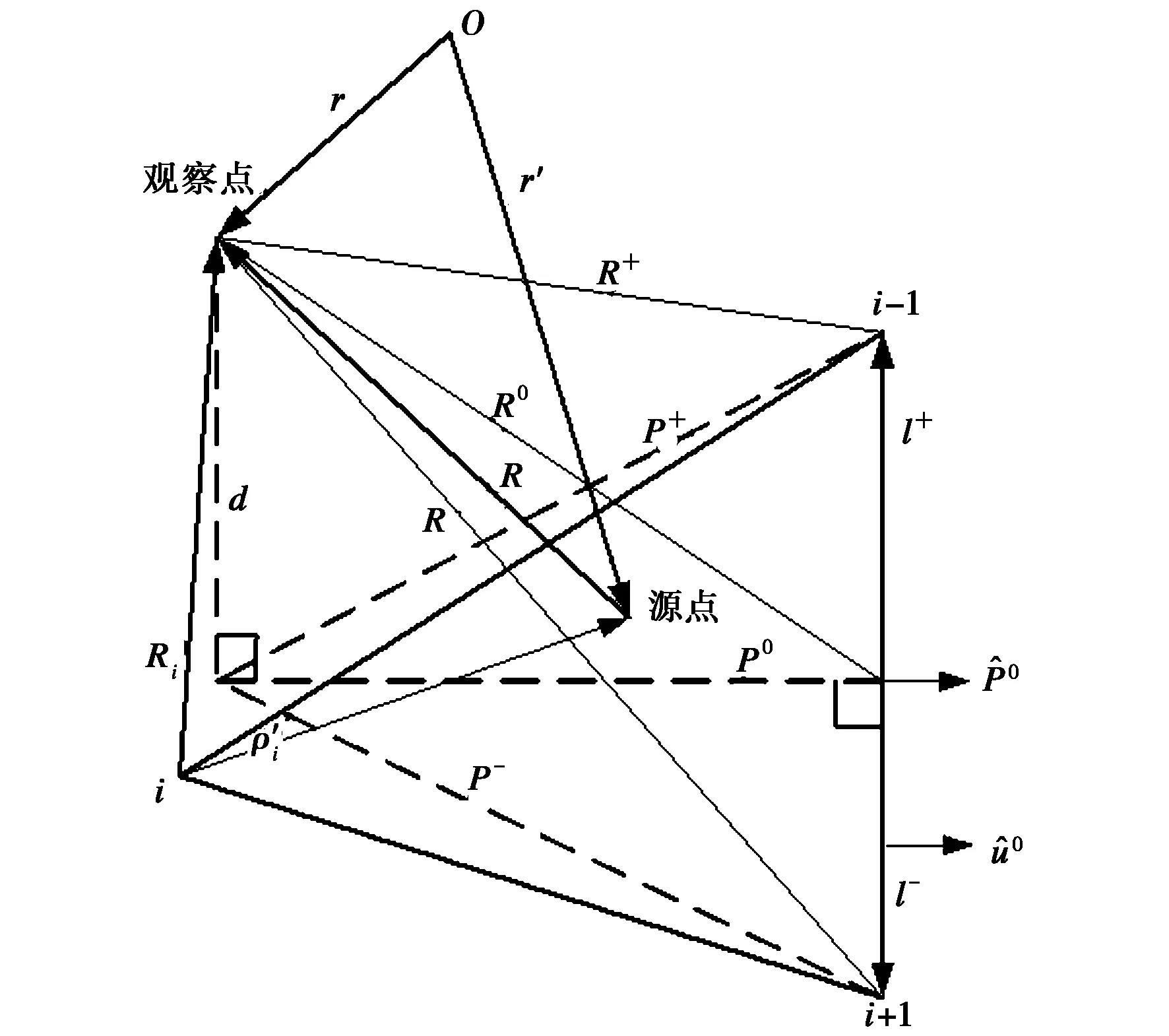
图1 观察点与源点各矢量及标量含义示意图

由式(5)可以看出，MFIE包含 1/R2的奇异点，因此当R→0需进行奇异点处理，即将式(5)右边展开为两部分，使前半部无奇异性,有

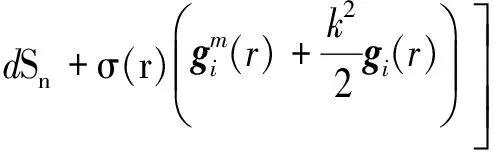
(6)

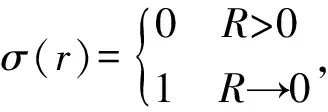
(7)

=g1i+g2i.

(8)

(9)

(10)

(11)

(12)

通过上述推导，去除了MFIE中内层积分的奇异性，采用高斯积分计算内层积分，可以完成矩量法基于RWG基函数计算MFIE. 但仅处理内层积分的奇异性无法获得精确计算结果.

2.2 外层积分弱奇异性处理

文献[7]推测MFIE无法获得精确结果是由于MFIE的积分核奇异性过强，即使处理了上述的内层积分奇异性，外层积分中仍然存在奇异性. 首先为检验此结论，不失一般性，单独对内层积分的奇异点 1/R2进行积分，其中积分源点和观察点分别为r=(x,y,0)，rd=(0,0,D) ，积分区域为一顶点位于原点，两边分别在x轴和y轴，边长为1的等腰直角三角形. 积分过程推导如下:

(13)

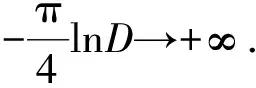
接着计算如图2所示两个三角形面片模型，当源点所在三角形a与观察点所在三角形b有公共边存在时，在b上沿公共边的垂线由近到远取多个观察点，分别带入阻抗矩阵Zmn的公式进行计算.

图2 共边的观察点、源点弱奇异性示意图

根据图2显示的计算结果，当观察点逐渐远离公共边，计算值趋于零；而当观察点接近公共边，计算值迅速下降，趋于负无穷，呈现对数函数形式. 可见2.1中的方法虽消除了MFIE中存在的强奇异性，但当源点三角形和观察点三角形共边时，确实仍存在ln(R) 形式的弱奇异性.

为解决此问题，文献[7]借鉴了加减奇异项的方法，从公式中分割出奇异项的分式单独分析. 但是MFIE表达式复杂，难以推导包含ln(R) 的解析表达式，并且外层积分的奇异性并不是标准对数函数，是否可以将 ln(R) 作为奇异项还有待验证.

这里通过对Hi(r) 的外层积分作积分域变换来解决上述问题. 将Hi(r) 与RWG函数做内积，得到它的外层积分，积分域为观察点所在三角形,有

(14)

首先对式(14)积分域作Duffy变换：

ξ=(1-y)x,η=y;

(15)

将积分域扩展为一个正方形，则积分式(14)变为

Hi(r)(1-y)dxdy.

(16)

对式(16)的积分上下限再作一次变换：

x=u2,y=y，

(17)

有

Hi(r)(1-y)2ududy.

(18)

Jacobi式为J2=2u，其中u将会与 ln(R) 的弱奇异性相抵消，从而去除积分式的奇异性.

上述方法解决了MFIE外层积分 ln(R) 形式的弱奇异性问题，相对于其它方法，积分域变换的方法更加简洁也更加严谨.

3 数值算例及结果分析

首先计算如图3所示球体的RCS并与Mie级数对比以验证算法的准确性. 球直径为1 m，剖分尺寸为0.06 m，剖分为2 724个三角形面片，未知数4 086个. 激励平面波的波长为1 m，由 -z方向入射，沿x方向极化.

如图3所示，本文方法计算MFIE的RCS结果与Mie级数解及EFIE吻合良好，与EFIE相比，均方根误差(RMS)=0.027 dB[11]. 图4显示MFIE在迭代求解时收敛速度远远快于EFIE.

接着计算如图5所示导弹模型，剖分尺寸为0.25 m，共剖分为3 420个三角形面片，未知数5 130个，入射波长4 m，由 -z方向入射，沿x方向极化. 计算其RCS时采用了三种矩量法：电场积分方程(EFIE)；未处理外层弱奇异性的MFIE(oldMFIE)；和处理了外层弱奇异性的MFIE(newMFIE).

由图5可见，未处理弱奇异性的MFIE计算RCS与EFIE的结果有明显差异，经过弱奇异性处理后的MFIE能与EFIE较好吻合，RMS=0.45 dB. 从图6可见MFIE在迭代求解时收敛速度远远快于EFIE.

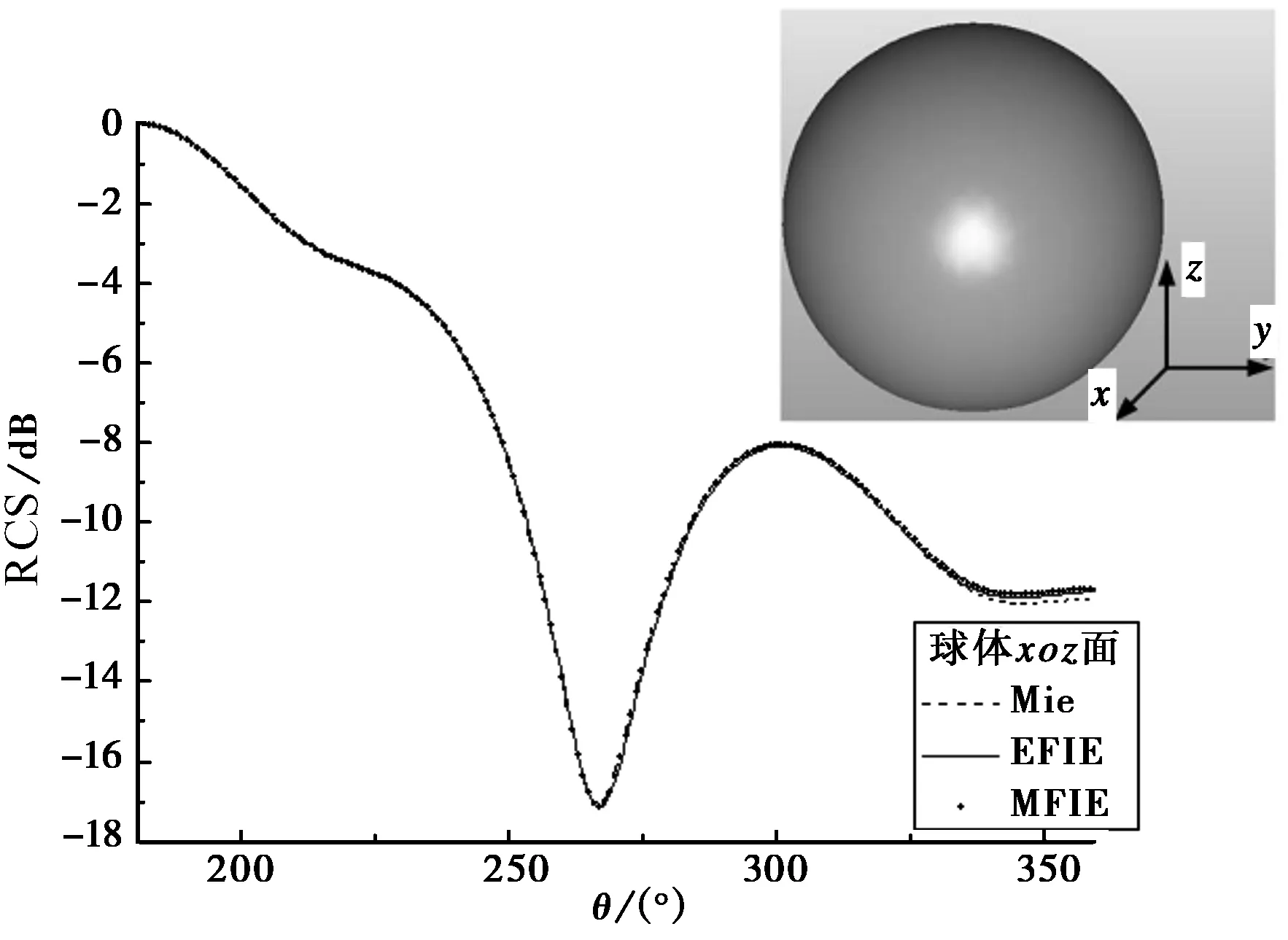
图3 球体xoz面上归一化RCS

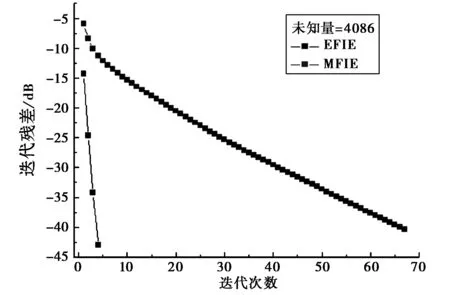
图4 计算球体RCS时广义最小余量法(GMRES)收敛速度

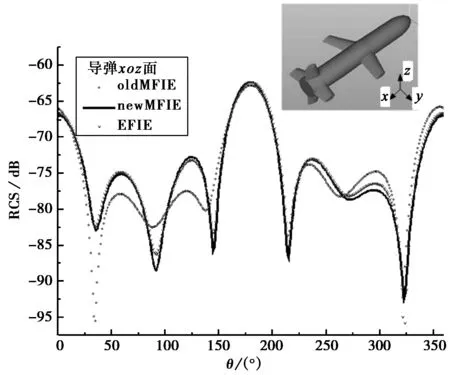
图5 导弹xoz面上RCS

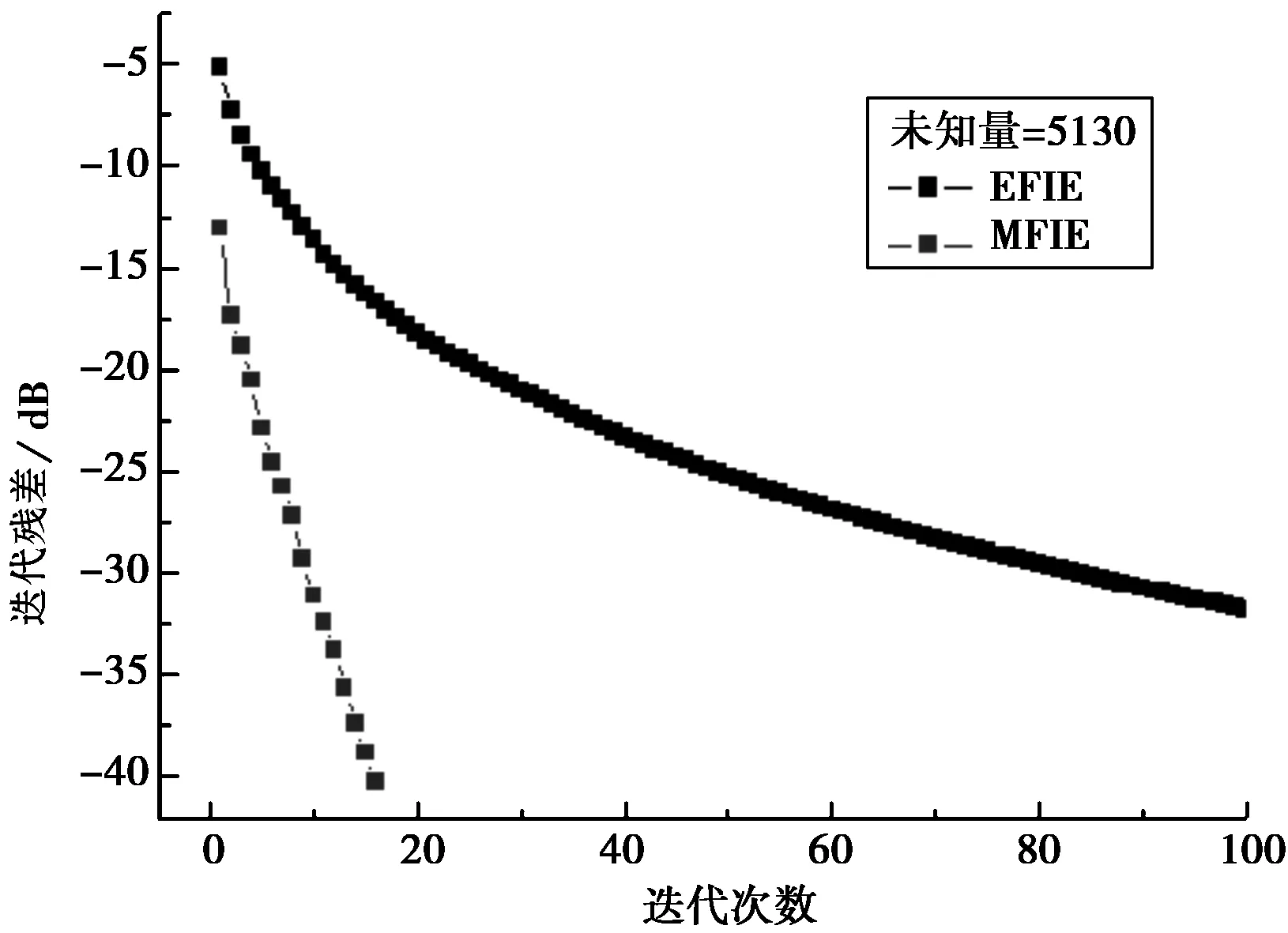
图6 计算导弹RCS时广义最小余量法收敛速度

4 结 论

针对矩量法求解MFIE计算结果不精确的问题，通过提取奇异点，消除了MFIE积分核所包含的1/R2强奇异性；并验证了外层积分中残留ln(R) 形式的弱奇异性，通过简单的积分域变换将其抵消，从而完全消除了MFIE的奇异性. 通过实例计算，验证了弱奇异性对于MFIE计算精度的影响，与EFIE结果的对比说明在完全消除奇异性后，矩量法求解MFIE可以达到较高的精度.

[1] HARRINGTON R F. Field Computation by Moment Methods[M]. New York: Macmillan, 1968.

[2] RAO S, WILTON D, GLISSON A. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Transactions on Antennas and Propagation, 1982, 30(3): 409-418.

[3] 凌 劲, 龚书喜, 王文涛, 等. 一种快速计算雷达散射截面空域特性的方法[J]. 电波科学学报, 2011, 26(1): 151-155.

LING Jin, GONG Shuxi, WANG Wentao, et al. A novel technique for fast radar cross section computation in spatial domains[J].Chinese Journal of Radio Science, 2011, 26(1): 151-155.(in Chinese)

[4] HODGES R E, RAHMAT-SAMII Y. The evaluation of MFIE integrals with the use of vector triangle basis functions[J]. Microwave Opt Technol Lett, 1997, 14(1): 9-14.

[8] KATAJA J, POLIMERIDIS A G, MOSIG J R, et al. Analytical shape derivatives of the MFIE system matrix discretized with RWG functions[J]. IEEE Trans Antennas Propag, 2013, 61(2):1-5.

[9] 徐晓飞, 曹祥玉, 高 军, 等. 基于核外求解方法的电大目标散射特性计算[J]. 电波科学学报, 2010, 25 (4): 679-683.

XU Xiaofei, CAO Xiangyu, GAO Jun, et al. Scattering calculation of electrically large targets based on out-of-core solving method[J]. Chinese Journal of Radio Science, 2010, 25(4): 679-683.(in Chinese)

[10] WILTON D R, RAO S M, GLISSON A W, et al. Potential integrals for uniform and linear source distributions on polygonal and polyhedral domains[J]. IEEE Trans Antennas Propa, 1984, 32(3): 276-281.

[11] 伍月千, 盛新庆. 均匀介质目标高阶矩量法的高效预处理方法[J]. 电波科学学报, 2012, 27(6): 1099-1104.

WU Yueqian, SHENG Xinqing. Efficient precondition algorithm for higher order method of moments for homogeneous dielectric objects[J]. Chinese Journal of Radio Science, 2012, 27(6): 1099-1104.(in Chinese)