一种基于对比度最优准则的调频斜率估计方法
徐志明 卢永革 李 胜 姚京萍
(电磁散射重点实验室,北京 100854)
引 言
合成孔径雷达(Synthetic Aperture Radar,SAR)是一种高分辨率有源微波成像雷达.它可以在能见度极差的气象条件下得到类似光学照相一样的高分辨率二维图像.SAR系统主要通过发射高带宽的线性调频信号和对方位回波历史相干处理来获取高分辨率二维图像.
在实际应用中,由于大气湍流的影响,雷达载机存在沿飞行方向和垂直于飞行方向的扰动,从而产生运动误差.运动误差带来的相位误差会破坏雷达回波信号的相干性,致使在成像处理中方位压缩的匹配处理出现失配,造成图像的方位向散焦,严重时甚至无法成像.因此,SAR图像处理中需要估计出回波方位向相位误差,并把它补偿掉.需要强调的是:影响图像聚焦性能好坏的主要因素是二次相位误差,即采用不精确的多普勒调频斜率值造成的相位误差.因此,准确地估计多普勒调频斜率是至关重要的.
图像对比度可理解为图像中各象素点亮度值与图像亮度均值的偏离程度,借助概率论中方差的概念,图像对比度函数是方位向图像亮度的标准偏差和平均值的比值,调频斜率的估计可等价为一个求解对比度值最优解的优化过程.而在这个优化过程中,随着对误差补偿精度要求的提高计算量会急剧加大.
本文根据图像对比度与调频斜率的关系,引入数学中的抛物线法来估计多普勒调频斜率,避免了经典算法中的反复迭代,大大提高了计算效率.最后用SAR实测数据验证了该方法的可行性和高效性.
1 对比度最优算法描述
散焦的合成孔径雷达图像,可以看作是目标散射系数与点扩散函数的卷积结果.扩散函数被展宽,散焦图像的像素幅度在其平均值上下表现出较小的起伏,图像对比度较低;聚焦良好的图像往往在一些像素上显示出尖锋,导致像素强度的较大变化,即对比度增大.因此,以对比度作为衡量图像聚焦程度的准则是可行的.
假定雷达数据中二次相位误差的数学模型为φe(n)=γ·n2(0≤n≤N).式中γ是二次相位误差系数,I(n,γ),(n=1,…,N)为方位向一维图像的幅度.
本文采用文献[3]中图像强度标准偏差与均值的比值作为图像对比度函数的定义为
(1)
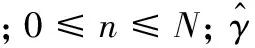
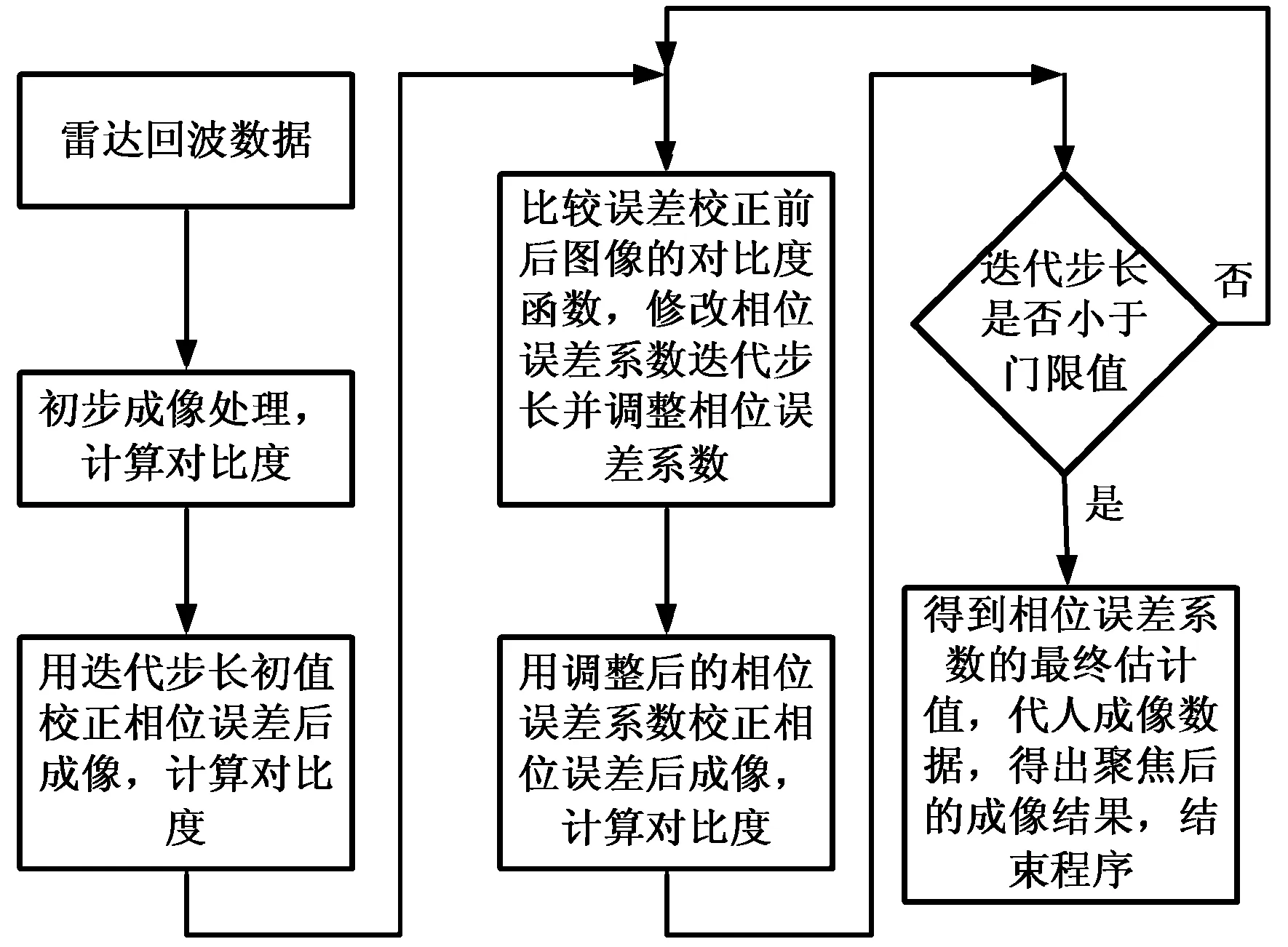
图1 对比度最优算法流程图
2 抛物线法
根据图像对比度定义,由点目标仿真可得到图像对比度与调频斜率的关系曲线如图2所示.当调频斜率为某一个值时,对比度有最大值,由此可以将图2近似为一条抛物线,若已知三个合适的试探调频斜率的对比度,则可以求出该对比度最大时所对应的调频斜率,此时,得到的调频斜率可以看作是最佳调频斜率的近似值.
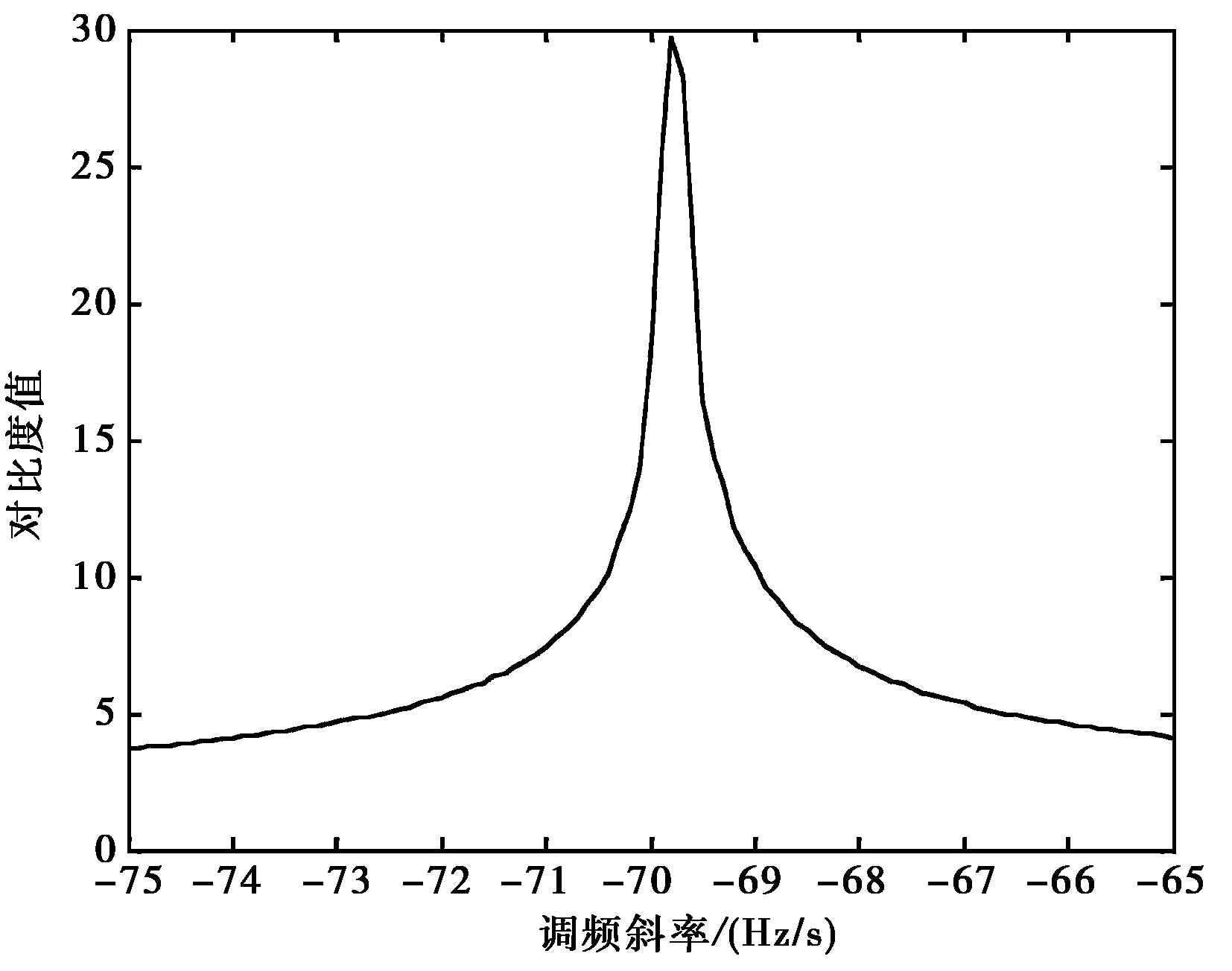
图2 对比度与调频斜率关系曲线图
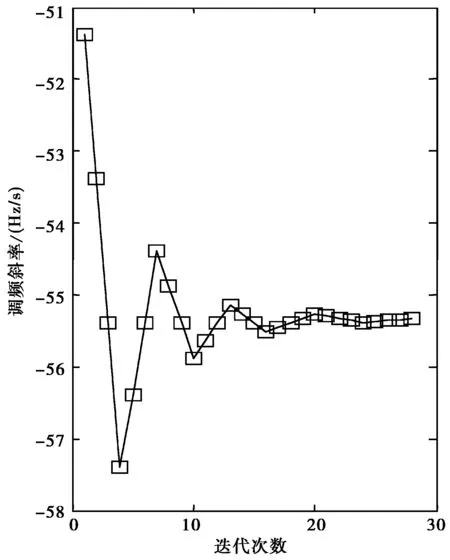
假设Ka1,Ka2,Ka3,(Ka1 (2) 由数学分析可知,式(2)达到最大值时对应的Ka值为 (3) 由此,可用该值来近似等于调频斜率的估计值. 因方法中三个试探调频斜率的取值影响抛物线法的估计准确度.实际应用中,可以根据机载SAR几何关系和各种运动传感器(如惯导、惯性测量单元等)测得的运动误差数据粗略估计调频斜率的范围.在此粗略的调频斜率范围附近取Ka1,Ka3,而Ka2可取Ka1,Ka3黄金分割值:Ka2=0.618(Ka3-Ka1)+Ka1. 图3 进退法自聚焦收敛需迭代的次数 为了分析抛物线法的可行性,本文分别用经典的进退法和抛物线法对X波段机载SAR实测数据进行了自聚焦分析.从图3可以看出,进退法要经过大约20次的迭代,调频斜率才差不多趋于收敛,且收敛值在-55.50 Hz/s附近.而抛物线法取Ka1=-50 Hz/s,Ka3=-61 Hz/s,Ka2=0.618(Ka3-Ka1)+Ka1,则可估计出调频斜率为-55.66 Hz/s.显然,两种方法估计得到的结果几乎一样,但抛物线法由于不需要迭代,计算效率明显增加,而成像结果近似.图4(a)是用经典的进退法成像的结果,图4(b)是用抛物线法成像的结果. (a) 进退法成像的结果 (b) 抛物线法成像的结果图4 实测数据成像结果 对图像中点目标分析评估结果如表1所示.在同样的计算机硬件平台上,很显然,根据评估指标可知,利用抛物线法成像得到的结果和经典的进退法得到的结果在成像质量上很接近,但是通过算法的运行时间可以看出,抛物线法的计算效率明显提高. 表1 两种算法分辨率及运行时间分析 同传统的图像对比度自聚焦算法相比,本文提出了基于抛物线法的图像对比度自聚焦算法,该方法引入了数学中的抛物线法来估计多普勒调频斜率,避免了传统算法中的反复迭代,大大提高了计算速度,明显缩短了图像的聚焦时间.通过机载SAR实测数据成像验证了该方法的可行性和高效性. [1] 武拥军,黄 冶,吴先良.机载双站聚束合成孔径雷达的三维空间分辨率特性[J].电波科学学报,2011,26(6):1200-1206. WU Yongjun,HUANG Ye,WU Xianliang.Three-dimensional spatial resolution of airborne bistatic spotlight SAR[J].Chinese Journal of Radio Science,2011,26(6):1200-1206.(in Chinese) [2] 邓云凯,王 宇,杨贤林,等.基于对比度最优准则的自聚焦优化算法研究[J].电子学报,2006,34(9):1742-1744. DENG Yunkai,WANG Yu,YANG Xianlin,ZHANG Zhimin.The Research of autofocus optimization algorithm based on contrast optimization criterion[J].Chinese Journal of Electronics,2006,34(9):1742-1744.(in Chinese) [3] BERIZZI F. CORSINI G. Autofocusing of inverse synthetic aperture radar images using contrast optimization[J].IEEE Trans AES,1996,32(3):1185-1191. [4] 刘月花,荆麟角.对比度最优自聚焦算法[J].电子与信息学报,2003,25(1):24-30. LIU Yuehua,JING Linjiao.Contrast optimization autofocus algorithm[J].Journal of Electronics and Information Technology,2003,25(1):24-30.(in Chinese) [5] 保 铮,刑孟道,王 彤.雷达成像技术[M].北京:电子工业出版社,2005. [6] 张澄波.综合孔径雷达:原理、系统分析与应用[M]. 北京:科学出版社,1989. [7] 杨 俭,侯海平,曲长文,等.机载下视阵列合成孔径雷达成像的微多普勒效应[J].电波科学学报,2012,27(5):1049-1055. YANG Jian,HOU Haiping,QU Changwen,et al.Micro-doppler effect for airborne downward looking array SAR imaging[J].Chinese Journal of Radio Science,2012,27(5):1049-1055.(in Chinese) [8] JAKOWTZ C V. WAHL DE, EICHEL P H,et al.Spotlight-Mode Synthetic Aperture Radar:A Signal Processing Approach[M].Boston,Kluwer Academic Publishers,1996.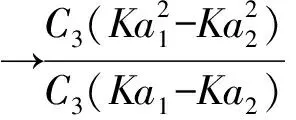
3 算法性能比较



4 结 论

