利用静态方向图数值综合方法抑制电离层干扰
陈骁锋 吴雄斌 徐兴安 沈志奔 王 立
(武汉大学电子信息学院海态实验室,湖北 武汉 430079)
引 言
电离层干扰一直是高频地波雷达探测海洋过程中非常重要的研究课题. 国内外关于此方面的研究主要围绕两个方面:一是电离层杂波特性的研究[1];二是电离层杂波的抑制方法研究[2]. 虽然国内外已经提出了许多抑制电离层干扰的方法,但由于电离层干扰的复杂性,大多数文献都是针对某段特殊的干扰数据进行分析,具有很强的针对性. 文献[3-5]尝试从阵列信号处理入手,通过控制雷达波束的方式,限制来自空中的电离层干扰,达到抑制的目的[3-5].
自适应阵列处理和空间谱估计是阵列信号处理的两个主要研究方向. 空间谱估计算法能够突破“瑞利限”实现高分辨的到达角方位估计,高频地波雷达在探测海洋表面流时,采用的就是空间谱估计算法中的多重信号分类法(Multiple Signal Characteristic,MUSIC). 然而在某些特定的环境下,空间谱估计算法由于存在探测信号源数必须小于天线阵元数的要求[4],会导致算法的失效,如利用宽波束雷达探测海洋表面的海浪. 此类情况下必须考虑用波束形成的方法,形成指定方向较窄波束的回波谱[5].
在理想条件下,自适应波束形成技术可以有效抑制干扰,使阵列输出信干噪比最大. 但实际系统中,不可避免的存在各种误差,如阵列通道的幅相误差、互耦误差、位置误差等,自适应的波束形成对这些误差干扰非常敏感[6]. 静态波束形成的方法与之相比,在实际应用中更加稳定,具有较好的鲁棒性.
空间匹配滤波器又称常规波束形成(Conventional Beamforming,CBF)是最基础的静态波束形成方法,它用对各阵元信号加权进行相位补偿的方法使主波束指向期望的信号方向. Dolph于1946年提出了用于均匀线阵的经典低副瓣综合方法(Dolph-Chebyshev方法),该方法可以在限定最大副瓣电平的同时获取较窄的主瓣波束[7]. 1966年Tseng和Baklanov将Dolph-Chebyshev方法推广应用于均匀矩形阵列[8-9]. 1990年Olen提出一种较为简单、直观的基于自适应阵列理论的静态方向图数值综合方法(Numerical Pattern Synthesis ,NPS[10]). 1992年Er提出的峰值控制方法可以在任意阵列情况下进行复杂静态方向图综合[11],但由于在每次迭代中需确定方向图的峰值点,因此较Olen的方法复杂. 2008年Eom利用遗传算法计算信号的最大功率,对相控阵天线单元的相位和幅度进行了优化和校正[12],2010年Frank用遗传算法形成二维平面阵的窄波束平覆盖区域[13].
在实际应用过程中,高频地波雷达回波信号处理中的波束形成方法,都只考虑一维即水平方向上的影响,这样导致的结果是尽管水平方向图具有窄波束、低旁瓣等优势,但来自空中的干扰也会大量进入到回波信号中,其中最典型的就是电离层干扰[14]. 特别对于小阵列而言,因为场地有限,往往只能采用双排阵列,导致阵列方向图在俯仰角方向上的分辨率非常低,严重影响回波特性.
针对这一问题,本文提出利用二维NPS算法对高频地波雷达回波信号进行波束形成,并针对NPS迭代过程中的性能变化特性,提出一种基于方向图旁瓣误差的性能模型,能够用于寻找NPS的最优设置参数. 分别针对方阵和特殊小型阵列进行了仿真分析,通过实测数据的比较,能够发现改进的二维NPS算法能够有效抑制来自垂直方向的干扰,为海洋信息的提取提供可靠的保障.
1 原理算法
首先介绍任意阵列雷达信号的数学建模,分析利用二维NPS算法进行波束形成过程中的主要步骤及关键问题.
对于一个N元任意窄带信号,导向矢量可以表示为
a(θ,φ)=[g1(θ)ejφ1(θ,φ),g2(θ)ejφ2(θ,φ),
…,gN(θ)ejφN(θ,φ)].
(1)
式中:gi(θ)为第i个阵元的响应;θ表示水平入射方位角;φ表示俯仰角;φi(θ,φ)为第i个阵元相对相位参考点的相移. 设阵列权矢量W=[w1,w2, …,wN]T, 则阵列响应方向图可表示为
G(θ,φ)=|WHa(θ,φ)|.
(2)
设(θ0,φ0)为期望信号角度,即归一化处理后有G(θ0,φ0)=1. 第一次迭代时的初值为
(3)
设D(θ,φ)为期望的旁瓣峰值电平,以dB表示,则实际电压值为
d(θ,φ)=10D(θ,φ)/20.
(4)
根据经典的NPS算法,在阵列的旁瓣区施加多个虚拟干扰,并控制虚拟干扰功率的大小,经过迭代运算,适当的调整该位置的干扰强度,从而得到期望的阵列天线方向图. 若第k次迭代求得的自适应权矢量为WH(k),则第k次迭代的方向图增益为
G(θ,φ,k)=|WH(k)a(θ,φ)|
(5)
根据式(5),可以确定出主瓣范围. 由于二维方向图的主瓣是一个放射性的波束,主瓣范围的确定相对一维来说复杂许多. 虽然一些方法如图像处理技术中的灰度阈值法、模式识别法[15]等,能够更准确地确定主瓣范围,但此时主瓣范围的表示形式也更加复杂. 因为每次迭代都需要进行主瓣区域的确定,所以,需要根据实际情况采用合适的方法,使时间复杂度不至于过大,又保证迭代结果的质量.
为了算法简便,只提取阵列水平平面和法线方向的垂面这两个平面,利用差分法分别检测主瓣附近的变化趋势,从而确定包络主瓣的方形区域[θL,θR,φL,φR].
假设M个干扰均匀分布在整个空间区域,入射角扫描个数为P,俯仰角扫描个数为Q,M=P×Q. 对于处于主瓣范围内的虚拟干扰,令其功率为0;对于主瓣范围外的干扰,通过比较虚拟干扰环境对应的方向图在旁瓣(θm,φm)处的增益G(θm,φm)与期望的旁瓣增益d(θm,φm)的大小,对虚拟干扰的功率进行调整. 虚拟干扰功率的迭代公式为
Γ(θp,φq,k)=ξ(θp,φq,k)+η[G(θp,φq,k)-
d((θp,φq))],
ξ(θp,φq,k+1)=
(6)
式中:η为一合适的常数因子,η的取值既要保证迭代的收敛性,又要保证收敛的速度,通常通过试验经验获得;p和q表示方位.
因为假设的虚拟干扰和噪声互不相关,可以得到第k次迭代的阵列协方差矩阵
aH(θp,φq)].
(7)

(8)
最终迭代结束时得到的自适应权矢量即为所求的静态权矢量.
2 仿真与实测数据分析
2.1 性能仿真
为验证二维NPS波束形成算法的性能及其对OSMAR071天线阵列的适用性,利用两种不同大小、规格的阵型(8×8方阵和OSMAR071天线阵)对算法进行仿真分析,给出两种阵列的二维CBF和NPS的方向图结果以便比较. 同时仿真不同方向图下存在电离层干扰的信号反演结果,利用蒙特卡洛算法比较两种方法的性能.
1) 8×8元方阵
取8×8元方阵,阵元间距为半波长,主瓣指向阵列法线方向(方位角90°,俯仰角0°),设置旁瓣峰值为-40 dB,迭代次数k=1 000次,每隔一个方位角、一个俯仰角取一个虚拟干扰,迭代的常数因子为η=0.1.
图1(a)、(b)所示为8×8元阵列二维CBF和二维NPS仿真结果的比较. 8×8元阵列二维NPS的结果与二维CBF的结果相比:①NPS水平方向的旁瓣波束得到有效的降低,旁瓣电平下降了约7 dB;②NPS俯仰角方向上的旁瓣得到有效抑制,特别对于俯仰角较大的区域,能够达到10 dB以上的抑制.
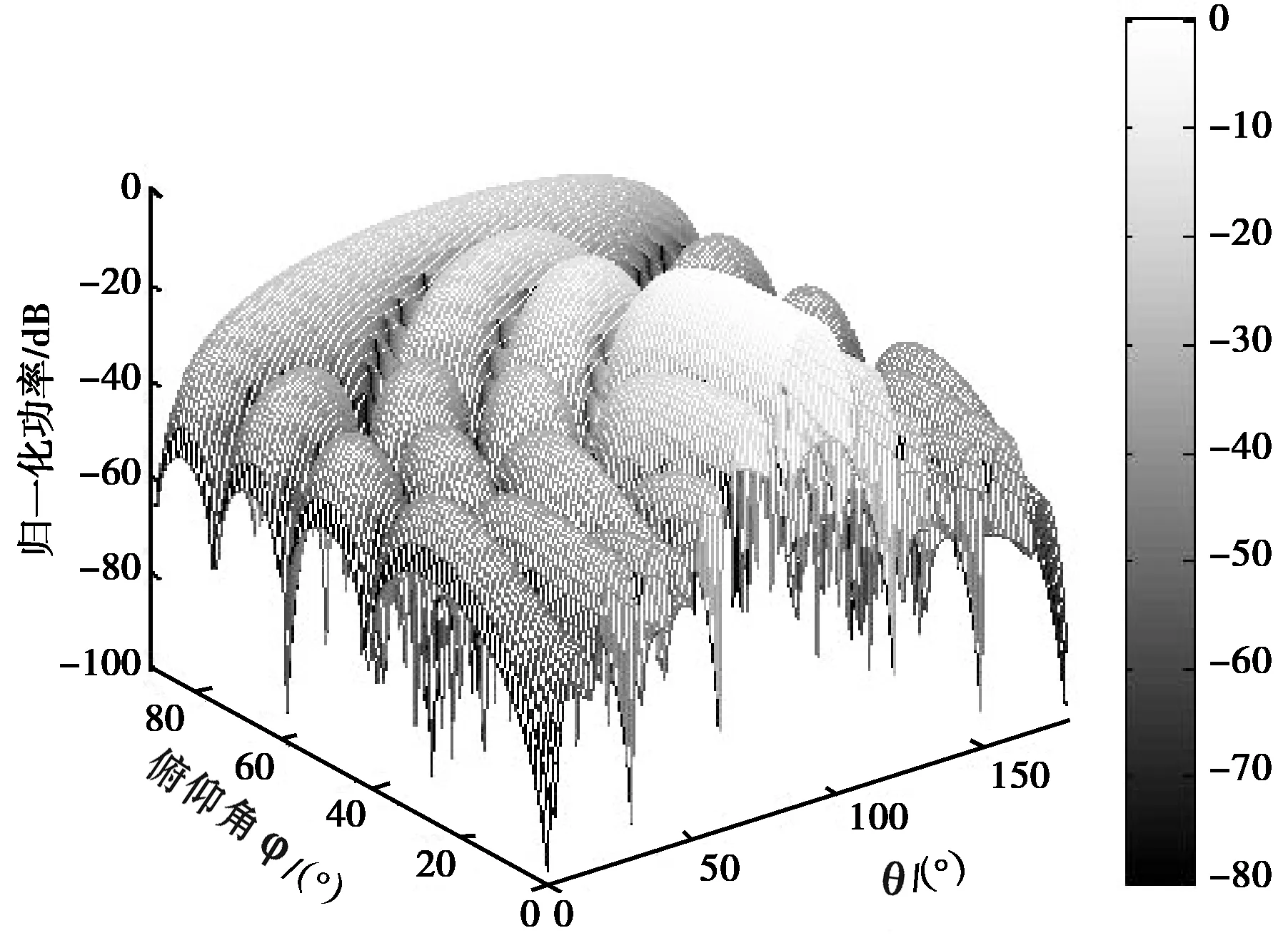
(a) 8×8元阵二维CBF方向图

(b) 8×8元阵二维NPS方向图
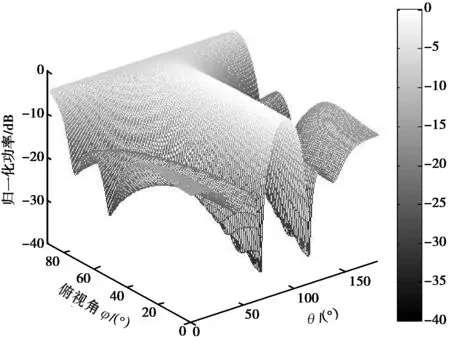
(c) OSMAR071二维CBF方向图

(d) OSMAR071二维NPS方向图图1 两阵列二维CBF和二维NPS仿真结果
2) OSMAR071天线阵
OSMAR071天线阵的阵型坐标如表1所示,工作频率为8 MHz,主瓣指向阵列法线方向(方位角90°,俯仰角0°),设置旁瓣峰值为:-15 dB(方位角0°~180°,俯仰角0°~5°),-10 dB(方位角0°~180°,俯仰角6°~90°),迭代次数k=1 000次,每隔一个方位角、一个俯仰角取一个虚拟干扰,迭代的常数因子为η=0.1.

表1 OSMAR071天线阵天线位置示意图 m
图1(c)、(d)所示为OSMAR071天线阵二维CBF和NPS仿真结果的比较. OSMAR071天线阵二维NPS的结果与二维CBF结果相比:① NPS水平方向的波束旁瓣电平相比CBF要高2~3 dB,且主瓣宽度明显增大,达到26°,-3 dB处主瓣宽度变大2°;②NPS俯仰角方向上的旁瓣得到有效抑制,能够达到5 dB以上. 产生这一现象的原因是OSMAR071的小型天线阵列只有两排,在空间的上分辨率非常低,水平方向和垂直方向的方向图相互制约,强制优化俯仰角方向的旁瓣,会导致水平方向的方向图优化效果变差.
由图1可以发现:两种算法在不同阵列下的效果是不同的,在8×8元阵列中,二维NPS算法能够很容易实现方向图的优化;而在OSMAR071小型阵列中,在对俯仰角较大区域的干扰进行抑制的时候,由于小型阵列的阵型限制,不可避免地会使水平方向的性能下降.
在仿真的过程中还发现,通过控制不同方位的虚拟干扰功率大小,得到的方向图效果是不同的,仿真设置是虚拟功率为-15 dB(方位角0°~180°,俯仰角0°~5°)和-10 dB(方位角0°~180°,俯仰角6°~90°),只是一个粗糙的仿真设置. 如果合理选用一些参数优化算法,对虚拟干扰平面进行细致的设置,会得到性能更好的方向图.
同时在迭代过程中,方向图的变化并不是平缓的,在8×8元阵列k=504及k=918仿真时,会出现旁瓣电平突然变大,然后再缓慢减小的现象.
这些现象说明,在利用二维NPS对阵列进行波束形成时,必须针对实际情况,设置更加合理的参数设置,以寻求最合适的优化结果.
3) 电离层干扰抑制性能仿真
为了进一步比较两种算法对电离层干扰抑制的效果,特构造一个存在噪声时的正弦信号模型. 该信号的幅度为1,频率为归一化-1,方位角为60°,俯仰角为0° ;电离层干扰的幅度为0.000 1,频率为覆盖频段上的均匀随机分布,方位角覆盖宽度为60°,俯仰角为80°;随机白噪声的幅度为0.001.
图2(b)中的电离层干扰的方位角位置为-30°~30°,图2(c)中的电离层干扰方位角为-180°~180°内随机起始位置,覆盖宽度为60°. 可以看出二维NPS算法与二维CBF算法相比,能够更好的抑制来自空中各个方向的电离层干扰,提高信号的信噪比.

(a) 无电离层干扰下波束形成图

(b) 电离层干扰下波束形成图

(c) 1 000次实验噪声变化图2 电离层干扰抑制性能仿真
针对参数选择的问题,提出一种方向图的旁瓣误差模型用以评估性能,以寻找最优参数设置. 下面以8×8元阵列为例进行说明.
首先定义水平视角和法线垂直视角两个方向从归一化零值开始搜索最小值和变化最大值,取这两个值中较小的一个,作为该指向方向的主瓣边界,定义垂直和水平方向的主瓣边界所在矩形区域为主瓣区间. 然后确定最小迭代次数N及最大迭代次数M,8×8元阵列元阵列的最大迭代次数一般不超1 000. 第k次迭代的方向图旁瓣误差模型Ek定义为主瓣区间外的电平值与预期电平值(即预设虚拟干扰值)的差值. 则
Ek=Γk-Γ0.
(9)
如图3(a)所示为旁瓣误差随迭代次数变化的曲线,此处没有采用绝对值和对数是因为曲线与预设虚拟干扰值Γ0有关,如将虚拟干扰值设置为-20 dB,则曲线会整体小于零.

(a) 不同虚拟干扰下的旁瓣误差
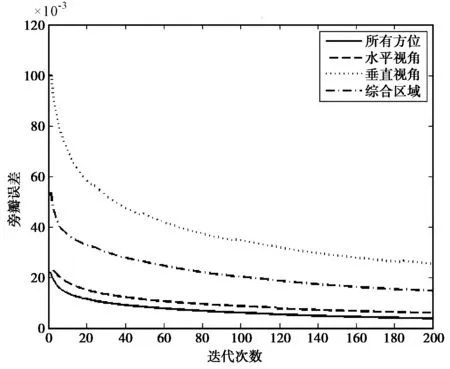
(b) 不同覆盖区域下的旁瓣误差
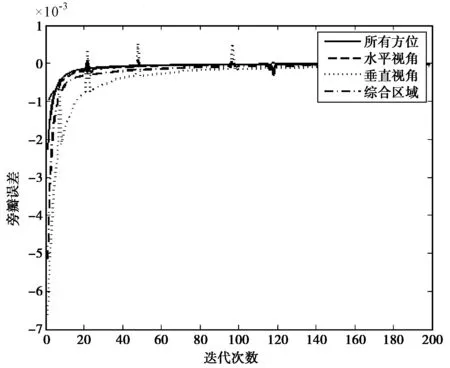
(c) 不同覆盖区域的旁瓣误差的导数图3 利用方向图旁瓣误差模型确定迭代次数
针对实际情况,模型还可以更改覆盖区间,如3(b)图所示为四种不同覆盖区域的旁瓣误差变化曲线(所有方位:方位角0°~180°、俯仰角0°~90°;水平视角:方位角0°~180°、俯仰角0°;垂直视角:方位角90°、俯仰角0°~90°;综合区域:俯仰角0°~5°及85°~90°时方位角为0°~180°、俯仰角6°~84°时方位角为主瓣边界内). 可以看出,所有方位和水平视角的曲线较为相似,垂直视角则误差较大. 此处建议采用综合区域.
为了确定迭代次数,先对上述曲线按照迭代次数作差,得到如图3(c)所示的变化率曲线. 规定若满足式(10)的条件,则认为曲线变化率已趋于平滑,此时迭代终止.
(10)
表2所示为设置不同最低门限时,迭代终止时的次数.

表2 不同最低门限时的迭代终止值
由式(9)可以看出,此模型实际上是不考虑预设虚拟干扰值的绝对影响的,而只是针对某个固定虚拟干扰值时的性能波动. 在对预设虚拟干扰值进行设定时,需要对模型进行功能扩展.
2.2 实测数据分析
为检验算法对于实测数据的效果,利用上述方法对位于福建龙海的中程高频地波雷达OSMAR071观测数据进行分析. 高频地波雷达OSMAR071是武汉大学电波传播实验室研制的阵列式OSMAR系列高频地波雷达的定型产品,回波信号质量较OSMAR工程样机有较大的改善[16]. 该雷达是采用FMICW波形的宽波束地波雷达,波束范围可达150°,扫频带宽为30 kHz,距离分辨率为5 km,接收阵列为8元非线性阵列,采用基于海洋回波的无源校准方法进行通道幅度和相位一致性校准后,利用MUSIC超分辨算法对海流进行测向,精度可达1.5°,该雷达每0.652 8×1 024 s可以得到一场多普勒谱数据.
图4为龙海雷达站2009年9月28日及2009年10月29日全天的实测数据,每个时间点的数据为该时刻回波二阶谱的频率叠加,并对每个时间点的数据分别作二维CBF和二维NPS波束形成. 图4(a)原始数据中4-6点时段存在点状干扰,10-18点时段存在条状干扰. 波束形成的主瓣指向阵列法线方向,工作频率为7.88 MHz,主瓣指向阵列法线方向(方位角90°,俯仰角0°);二维NPS算法设置旁瓣峰值为:-15 dB(俯仰角0°~5°),-10 dB(俯仰角6°~90°),迭代次数k=1 000次,每隔一个方位角、一个俯仰角取一个虚拟干扰,迭代的常数因子为η=0.1.
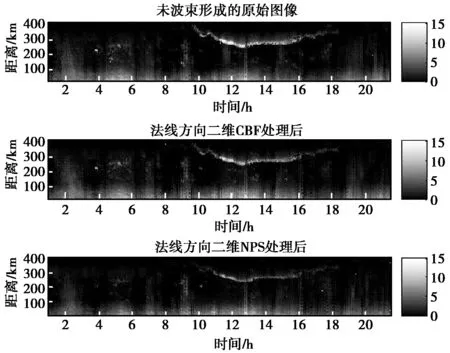
(a) 2009年9月28日全天的实测数据

(b) 2009年10月29日全天的实测数据图4 龙海雷达站回波能量图
比较结果可以发现,4-6点时段的点状干扰数量明显减少,10-18点时段的条状干扰颜色变浅. 同样的,图4(b)也显示出相同的性能. 这说明二维NPS能比二维CBF更有效地抑制点状干扰,并能够减轻条状干扰的影响.
3 结 论
提出利用二维静态方向图NPS对高频地波雷达回波信号进行数字波束形成,实现抑制电离层干扰的功能. 1)对于两种阵型进行了仿真分析,发现对于8×8元阵列,二维NPS算法性能优良,无论是在水平方向还是俯仰角较大的区域,都能够抑制旁瓣电平,降低干扰噪声对信号的影响;对于OSMAR071的小型阵列,需要仔细设置参数,特别是虚拟干扰功率大小,才能使综合性能最优. 2)提出了方向图旁瓣性能模型用来评估二维NPS算法迭代过程中的性能变化. 3)分析了两天的实测数据,结果表明二维NPS算法能够明显减小电离层干扰的影响. 在实际应用中展示出较为稳定可靠的性能.
由于实际电离层干扰的复杂性,抗干扰阵列的设计和算法的参数配置等需要进一步的研究. 今后还需要从以下问题开展进一步的工作:1)确定二维主瓣宽度的方法需要进行更多的比较尝试. 2)方向图性能模型的性能全面化,考虑抖动误差和绝对误差等多方面因素,便于迭代次数及虚拟干扰的选择. 3)由于现有实测数据中电离层干扰都处于300~400 km的较远区域,难以布设浮标获取对比数据. 同时海洋信息参数的获取率很低,无法进行海洋参数的结果比较. 应设法寻找其它形式的电离层干扰进行实测数据分析.
[1] 吴海鹏, 焦培南, 凡俊梅. 高频海洋回波谱电离层污染及实验研究[J]. 电波科学学报, 2004, 19(5): 515-518.
WU HaiPeng, JIAO Peinan, FAN Junmei. Effects of ionosphere on HF sea echo Doppler spectra[J]. Chinese Journal of Radio Science, 2004, 19(5): 515-518. (in Chinese)
[2] LI W L. High-frequency over the horizon radar and ionospheric backscatter studies in China[J]. Radio Science, 1998,33(5):1445-1458.
[3] VOURAS P, FREBURGER B. Application of adaptive beamforming techniques to HF radar[C]∥ IEEE Radar Conference, 2008: 795-800.
[4] STOICA P, NEHORAI A. MUSIC, Maximum likelihood, and Cramer-Rao bound[J]. IEEE Trans on Acoustics, Speechand Signal Processing, 1989, 37(5): 720-741.
[5] 李 伦, 吴雄斌, 李 炎, 等. “凤凰”台风期间海面风、浪的高频地波雷达OSMAR071遥感[J]. 遥感学报, 2012, 16(1): 154-165.
[6] 王永良, 丁前军, 李荣锋. 自适应阵列处理[M]. 北京: 清华大学出版社, 2009: 223-226.
[7] DOLPH C L. A Current distribution for broadside arrays which optimizes the relationship between beamwidth and side-lobe level[J]. Proc IRE, 1946, 34: 335-348.
[8] TSENG F I, CHENG D K. Optimum scannable planar arrays with an invariant sidelobe level[J]. proceedings of the IEEE, 1968, 56 (11): 1771-1778.
[9] BAKLANOV Y V. Chebyshev distribution of currents for a plane array of radiators[J]. Radio Eng Electron Phys, 1966, 11: 640-642.
[10] OLEN C A, COMPTON R T Jr. A numerical pattern synthesis algorithm for arrays[J]. IEEE Transactions on Antennas and Propagation, 1990, 38(10): 1666-1676.
[11] ER M H. Array pattern synthesis with a controlled mean-square sidelobel level[J]. IEEE Transactions on Signal Processing, 1992, 40(4): 977-981.
[12] SON S H, EOM S Y, JEON S I, et al. Automatic phase correction of phased array antennas by a genetic algorithm[J]. IEEE Antenas and Propagation Magazine, 2008, 56(8): 2751-2754.
[13] VILLEGAS F J. Parallel genetic-algorithm optimization of shaped beam coverage areas using planar 2-D phased arrays[J]. IEEE Trans on Antenna and Propagation, 2007, 55(6): 1745-1753.
[14] 尚 尚, 张 宁, 李 杨. 高频地波雷达电离层杂波统计特性研究[J]. 电波科学学报, 2011, 26(3): 521-526.
SHANG Shang, ZHANG Ning, LI Yang. Ionospheric clutter statistical properties in HFSWR[J]. Chinese Journal of Radio Science,2011,26(3):521-526.(in Chinese)
[15] RAFAEL C, GONZALEZ. 数字图像处理[M]. 北京: 电子工业出版社, 2002.
[16] WU X B, LI L, SHAO Y X, et al. Experimental determination of sinificant waveheight by OSMAR71: comparison with results from Buoy[J]. Journal of Wuhan University Nature Science, 2009, 14(6): 499-504.

