具有干扰和协方差反馈的多天线系统信道容量
王 谦 岳殿武,2 闫秋娜
(1.大连海事大学信息科学技术学院,辽宁 大连 116026;2.东南大学移动通信国家重点实验室,江苏 南京 210096)
引 言
随着对无线通信业务需求的日益增加,人们对传输速率等指标提出了更高的要求.理论研究表明多输入多输出(Multiple-Input Multiple-Output, UMIMO)多天线无线通信系统和传统单发单收单天线系统相比可显著提高系统的信道容量,因而MIMO技术成为当今无线通信领域的热门话题[1].
根据发射端对信道状态信息(Channel State Information,CSI)的掌握程度不同,MIMO信道容量存在很大差异.发射端获得CSI的程度大致分为三类:1)完全获知CSI;2)部分获知CSI;3)完全未知CSI.理论研究表明,在获得不同程度CSI情况下,发射端对发射信号协方差矩阵的构造方式存在很大差异,相应的信道容量也有很大区别[1].部分获知CSI是指发射端已知关于信道的统计信息,如关于信道的协方差信息.因为信道矩阵的相关性关于时间相对稳定,所以进行协方差反馈可以极大地减少额外开支,且系统相对便于实现.完全获知CSI系统性能最好,但实践难度最大;而完全未知CSI 时,理论比较容易展开,但实际性能要比部分获知CSI情况差很大[1-2].因此,这里将着重探讨最重要的部分获知CSI情况.
在无同信道干扰情况下,发射信号协方差矩阵完全决定于MIMO信道的统计特性[3-4].在瑞利衰落下,文献[3-4]将信道容量建立为矩阵变量的优化问题.其中文献[3]考虑了存在接收相关的MIMO信道,而文献[4]则将MIMO信道模型推广到既存在接收相关又存在发射相关的MIMO信道情况.此外,文献[3-4]还给出了利用协方差反馈所得最优发射信号协方差矩阵所具有的特征,以及在此情况下波束成型技术可以获得最优性能的充分必要条件.对于任意给定发射信号协方差矩阵,文献[5]则推导出遍历信道容量的闭式表达式.在赖斯信道下,MIMO信道容量取决于均值和协方差的反馈信息.由于在该信道下的分析难度较大,已知的研究或者对信道模型进行了简化[6],或者对发射信号进行了限制[7].其中文献[6]针对多输入单输出系统提出一种利用均值与协方差信息反馈的信道容量优化方案;而文献[7]则针对MIMO系统给出小信噪比下发射信号协方差矩阵的表达形式.通过利用遍历容量的二阶近似,文献[8]对容量的最优化问题进行了深一步探讨.
在现代通信系统特别是蜂窝移动通信系统中,为了提高频谱利用率,相距足够远的通信链路常采用相同的载频,这将不可避免地在通信过程中引入严重影响通信质量的同信道干扰[9].当存在同信道干扰时,相关结论还鲜有报导,所以,将探讨部分获知CSI情况下具有同信道干扰的MIMO遍历信道容量最优化问题.特别地通过已知的协方差信息,利用大数定理和非线性规划理论中的梯度映射算法,提出一种发射信号协方差矩阵的近似最优构造方式,并通过仿真分析给出一些相关性质.
1 系统模型
考虑一个具有M根发射天线和N根接收天线的MIMO系统,则发射端与接收端之间的信道可以用N×M的信道矩阵H表示.令其衰落统计为瑞利分布,发射端相关矩阵为Ωt,接收端相关矩阵为Ωr.现假设接收端的相关矩阵为单位对角矩阵,即Ωr=IN.这表示接收天线元素之间是统计独立的.该假设适用于接收天线距离较大的上行链路,即接收端为基站的情况.假设外界同信道干扰源个数为L,第i个干扰源具有Mi根干扰天线,其至接收端的信道矩阵为Hi,而矩阵Hi的内部元素服从独立同分布的瑞利衰落,这里i=1,2,…,L.则在接收端,N维接收信号向量y可以表示为
(1)
式中:ρ和ηi分别表示发射信噪比和第i个干扰源的干扰噪声比; 向量n表示高斯白噪声向量,它的协方差矩阵为IN;x和xi分别表示发射信号和第i个干扰源的干扰信号,二者均为零均值的高斯向量,具有的协方差矩阵分别为S和Si,i=1,…,L.最后假设Si=IMi/Mi,其中IM表示M阶的单位对角矩阵.由文献[10]可知,这是一种容量下界的情况.
假设接收端可以获得准确的CSI,而发射端仅获知信道发射端的互相关矩阵Ωt以及干扰功率ηi,i=1,…,L,根据信息论理论,条件互信息量可以表示为[1]
(2)
式中
(3)
所以遍历信道容量表示为[1]
I=E(IH,Hi,1≤i≤L)
(4)
式中E(·)表示统计平均.
2 遍历容量的近似最优化
首先考虑对同信道干扰成分的等效.当干扰天线数目很大时,因为矩阵Hi的元素服从独立同分布的瑞利衰落,所以由文献[1]的结论可以得到下列关系
(5)
将式(5)代入式(3),即得到
(6)
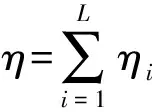
(7)
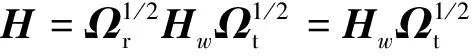
(8)
(9)
并将式(8)和(9)带入式(7),可得到
(10)
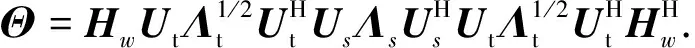
(11)
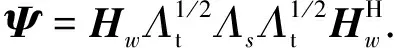
令Λs=diag(s1,…,sM),Λt=diag(t1,…,tM).同时为了便于书写,令s=(s1,…,sM)T,t=(t1,…,tM)T.遍历信道容量的最优化问题就化为了以下问题:
s.t.s1+…+sM=1,
si≥0,i=1,…,M.
(12)
令满足式(12)限制条件的所有元素的集合为Δ.
对于式(12),至今最优解向量s仍然无法利用闭式表达[4],所以与文献[11]的分析思路相似,将利用梯度映射算法,通过迭代实现遍历信道容量的优化.
首先,定义下列符号,以引出遍历容量的闭式表达式.令
(13)
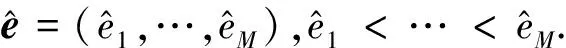

利用文献[5]的结论,当M≤N时,遍历容量表达式为
(14)
式中:Φ1(k)的(i,j)位置的元素
{Φ1(k)}i,j=
(15)
(16)
(17)
至于M>N的情况,将在附录中给出表达式.
梯度映射算法常用于求解带有约束条件的函数最优值问题,该算法是最速下降法在约束条件下的延伸[15].在上文背景下,其步骤如下:
1) 设定最大迭代次数kmax和起始点s(0)=(s1(0),…,sM(0))T,使其满足s(0)∈Δ,此时令k=0.
2) 计算遍历容量表达式I在点(s1(k),…,sM(k))处的梯度g.则g可以表示为
(18)
3) 选择合适的γk,并令
s′(k)=s(k)+γkg(k).
(19)
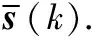
5) 选择合适的αk,并令
(20)
6) 令k=k+1,检查k是否达到了最大迭代次数kmax,如果达到kmax则退出迭代;如果未达到kmax,则检查s(k+1)-s(k)中最大元素的取值δ,如果δ大于预设值ε,则回到第2步;如果δ≤ε,则退出迭代.
在进行上述算法的过程中,主要涉及如下4方面内容:
1) 初值的选择和对向量的排序问题;
2) 导数的求解;

4) 如何选择合适的步长αk.
下面对以上问题逐个进行解决.
2.1 初始值的选择和对向量元素的排序
2.2 导数的求解
为了便于分析,分别考虑式(14)的分子和分母部分.
对于分母部分,令
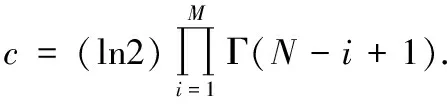
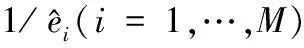
(22)
(23)
(24)
(25)

(26)
对于分子部分,令
F2(k)=det(Φ1(k)),
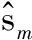
(27)
{F2(k,r,m)}i,j=

(29)
(30)
(31)
I1(n,u,b)= (-1)n-1bnebuEi(-bu)+
(32)
(33)

(34)
2.3 映射
应用文献[11]可以得到
(35)
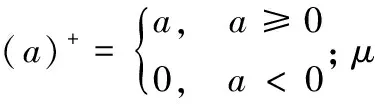
(36)
不难看出,式(36)是μ的单调递减函数,而μ的取值可以利用二分法[16]获得.
2.4 步长αk的确定
利用Armijo法则[15]可获得步长αk.在算法迭代过程中,令γk=1,β是取值在0.1到0.5之间的常数,σ是取值在0到1之间的常数,并令αk=βmk其中mk的取值即为最小的使不等式(37)成立的非负整数.
I(s(k+1))-I(s(k))
(37)
3 仿真结果
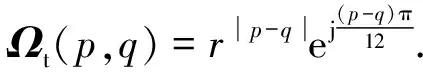
首先观察本文方法的容量性能,并与完全获知CSI、完全未知CSI两种典型系统容量进行对比.为便于说明,分别简称以上两种系统为Ⅰ系统和Ⅱ系统,而本文方法对应的系统简称为Ⅲ系统.Ⅰ系统容量通过广义注水算法(Ceneralized Water Filling,GWF)获得[11];Ⅱ系统容量通过信号协方差矩阵取单位对角矩阵获得[1].
图1比较三种系统的遍历容量.图中每个系统含有2根发射天线和2根接收天线,发射信噪比为10 dB,r=0.9,共有2个等功率干扰源,每个干扰源带有2根干扰天线.通过观察可以发现,Ⅲ系统的容量始终介于Ⅰ系统和Ⅱ系统容量之间.
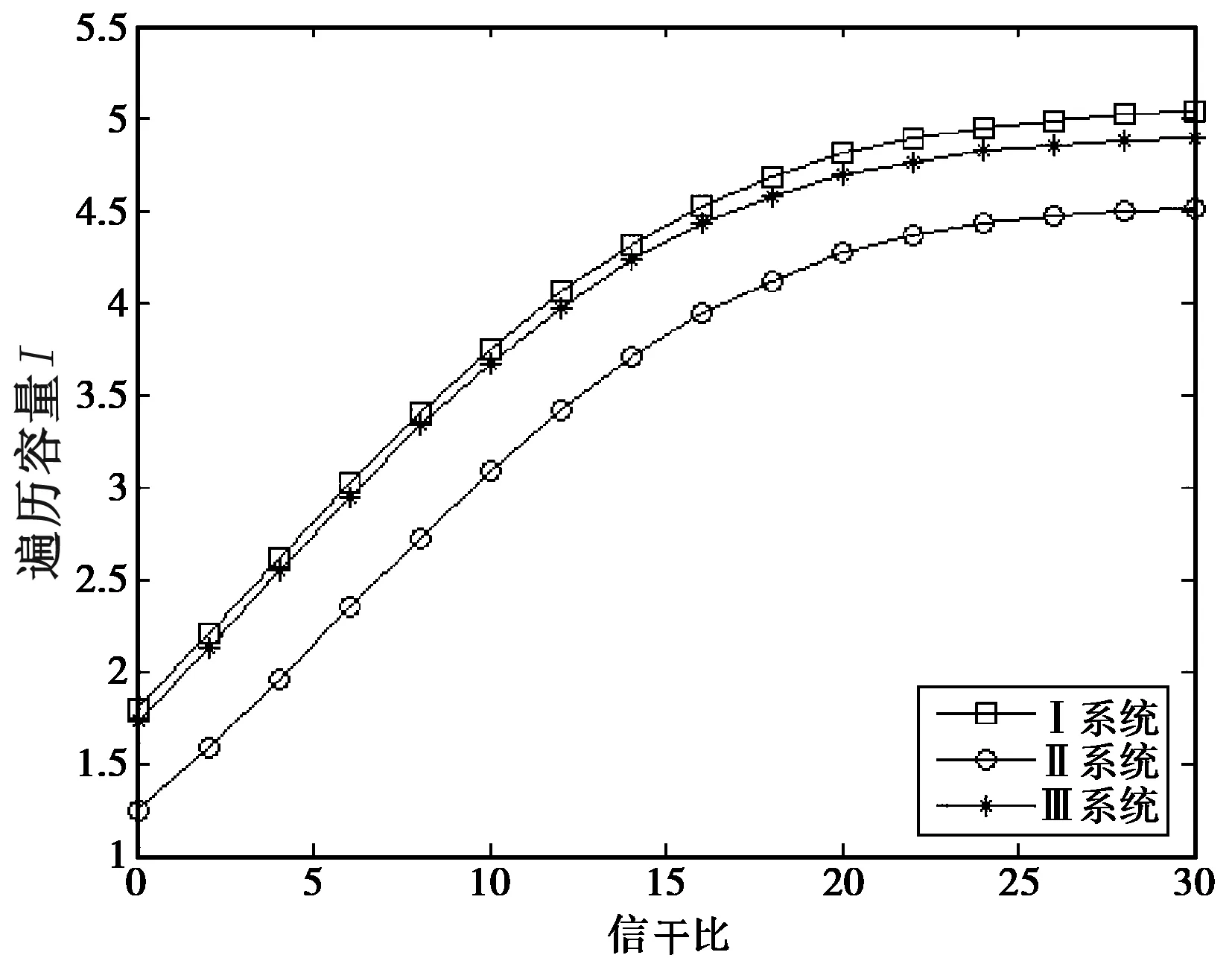
图1 三种系统容量比较
为了考察Ⅲ系统的实用性,我们从信噪比、干扰源天线数以及相关系数三方面进行仿真.为了便于比较,定义Ⅲ系统的容量为CGP,I系统的容量为CGWF,Ⅱ系统的容量为CNoCSI,并定义容量比x1=CGP/CGWF,容量比x2=CNoCSI/CGP.容量比x1表示Ⅲ系统容量与Ⅰ系统容量接近程度;而容量比x2表示Ⅱ系统容量与Ⅲ系统容量的接近程度.
图2,3和4分别比较信噪比,干扰天线数目以及相关系数r对x1的影响.仿真过程假设收发天线数相等,均为2.图2中令干扰天线数目为2,r=0.1.图3中信噪比为20 dB,r=0.1,并且横轴的SIR表示信号总功率与总干扰功率的比值.图4中信噪比取20 dB,干扰天线个数为2.由仿真曲线可以看出:信噪比的取值越大以及干扰天线数目越少,Ⅲ系统容量与I系统容量越接近;而相关系数对性能的影响则相对复杂,通过曲线可以看出:在低信干比即强干扰处,r的取值越大,两系统的容量性能越接近;当信干比取值较大即干扰较弱时,结论恰好相反.由此可得,在强干扰和强相关以及在弱干扰和弱相关情况下,Ⅲ系统容量将接近I系统容量.
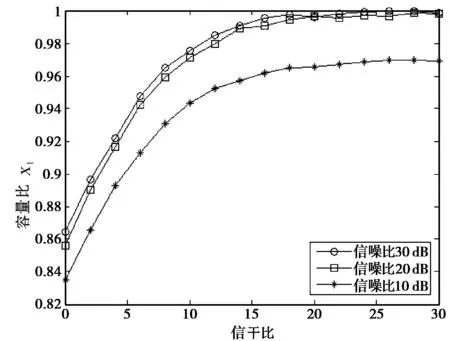
图2 Ⅲ系统与Ⅰ系统容量比随信噪比变化情况
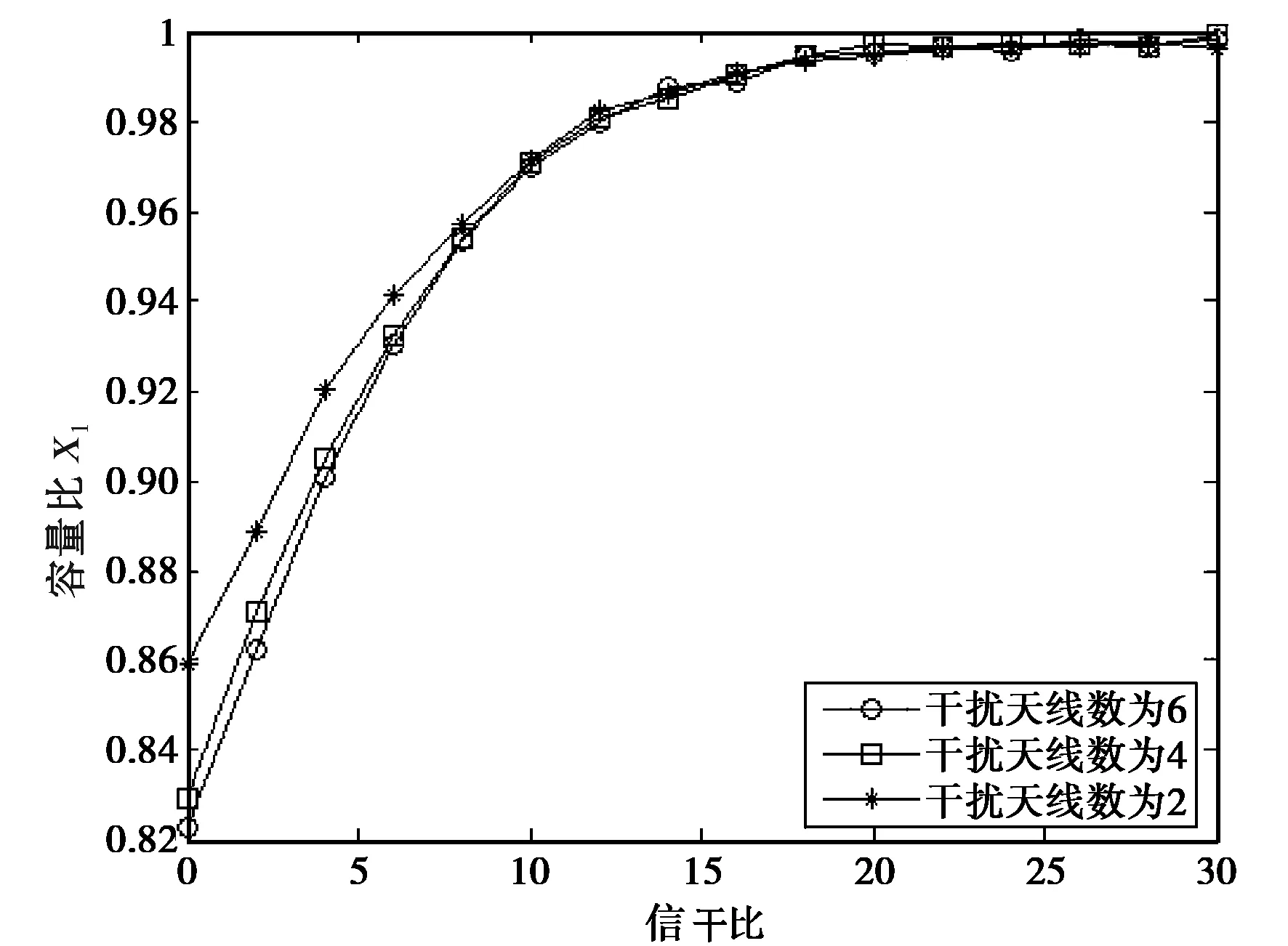
图3 Ⅲ系统与Ⅰ系统容量比随干扰天线数目变化情况
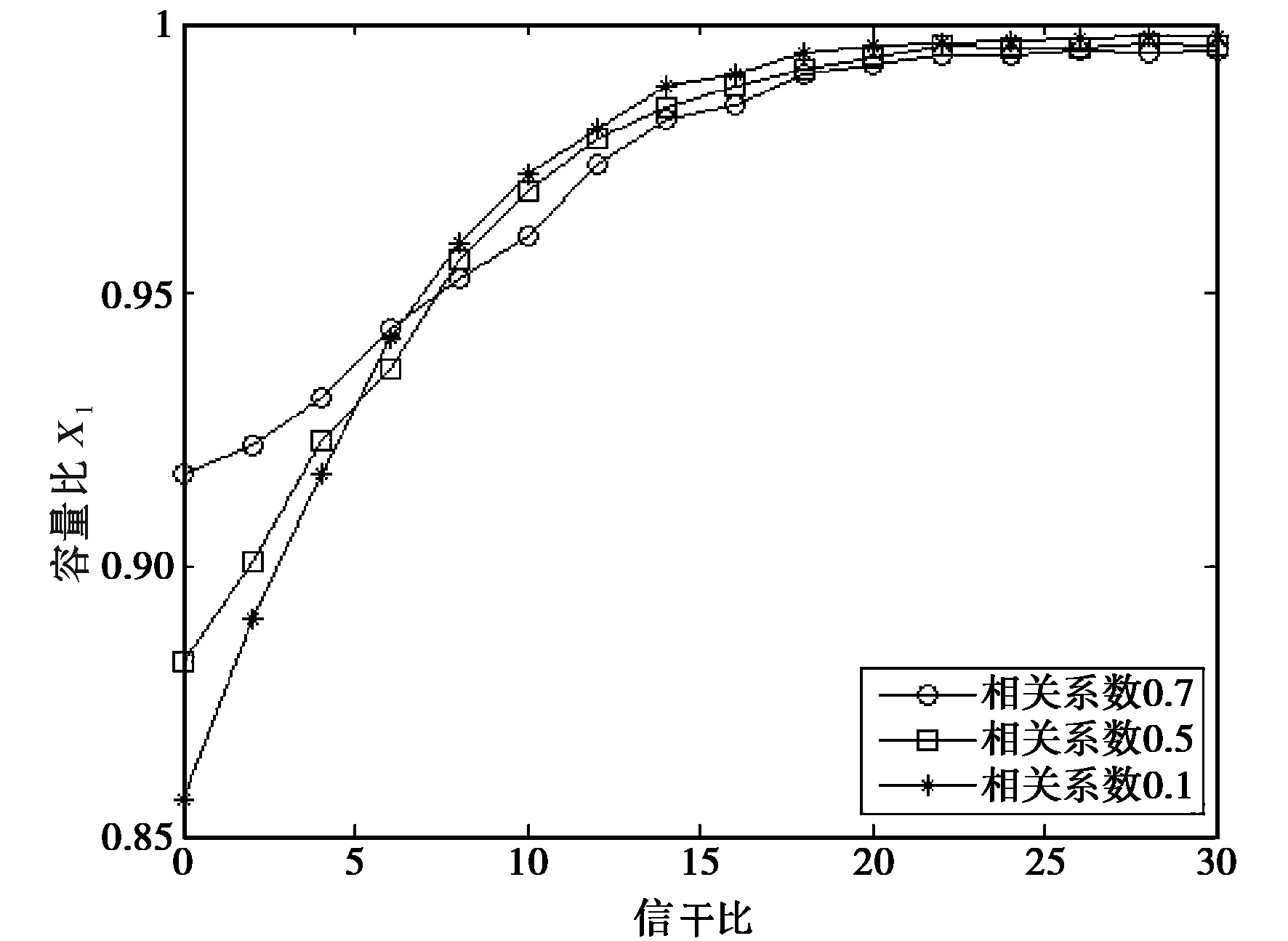
图4 Ⅲ系统与Ⅰ系统容量比随相关系数变化情况
我们也分别观察了信噪比、干扰天线数目以及相关系数r对x2的影响,相应的关于容量比x2的仿真结果分别类似图2,3和4.这些仿真结果可以总结为,在强干扰和很强的相关特性时,x2的取值较小,Ⅲ系统容量相比II系统容量明显提高.
综上可以得出,在强干扰以及信道矩阵具有很强相关性时,我们所考虑的协方差反馈系统具有很高的实际应用价值.
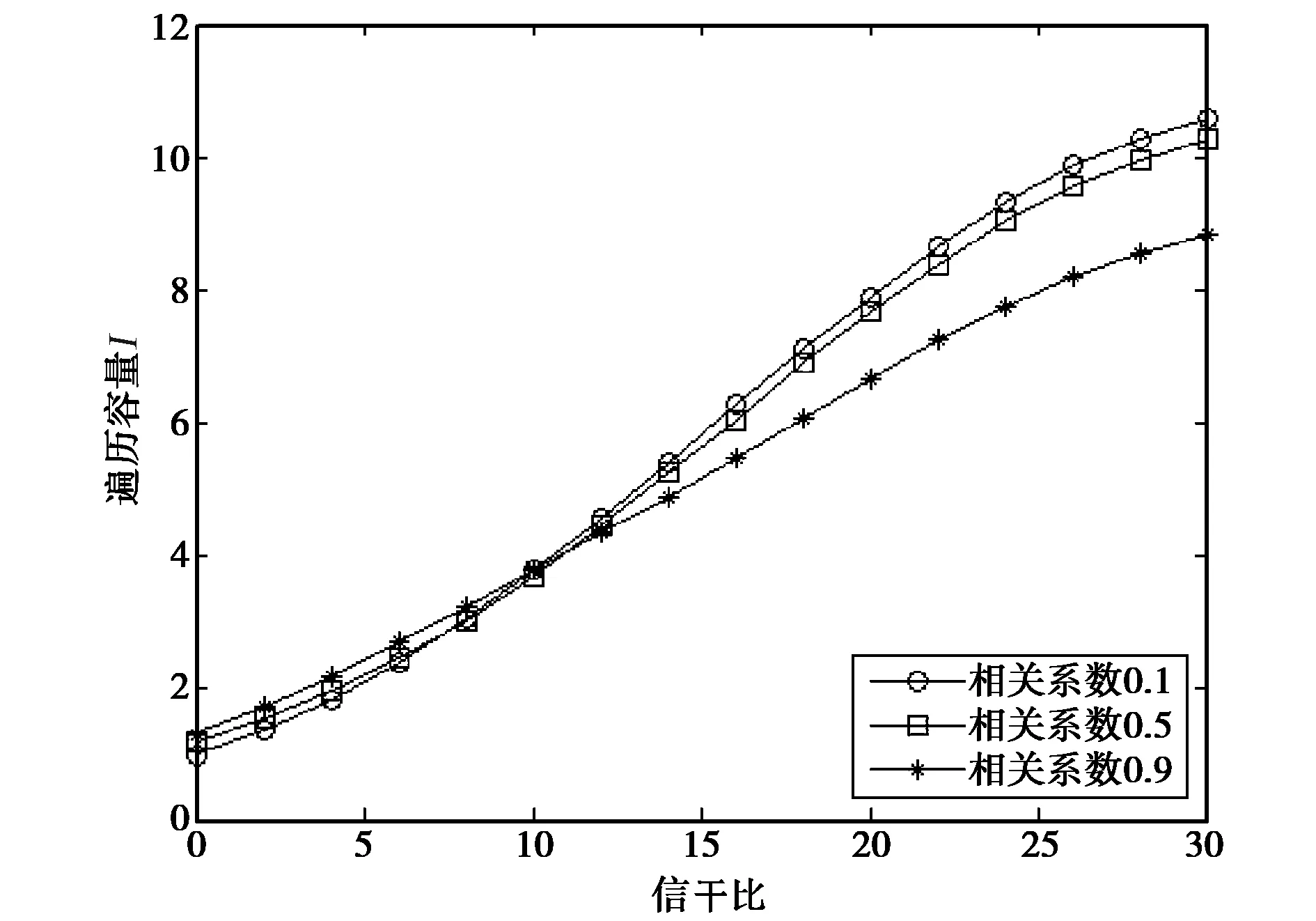
图5 Ⅲ系统容量随信道矩阵相关系数r的变化情况
下面通过Monte-Carlo仿真观察Ⅲ系统容量随信道矩阵相关系数r的变化情况,图5考虑2发2收的MIMO系统,发射信噪比为20 dB,系统带有3个干扰源,每个干扰源装备2根天线.由仿真结果可以看出,当SIR大于一个取值后,容量取值将随r的增加而减小,当SIR小于这个取值时,结论恰好相反.
在实际通信链路中,干扰信道往往具有发射相关性,干扰信号协方差矩阵Si取值也往往与本文的假设不同,由文献[10]可知,该遍历容量性能将优于此前讨论的情况.为了便于讨论,定义IV系统如下:所有干扰信道的发射相关矩阵为指数模型并且相关系数ri都相等,Si为利用天线数归一化的单位对角矩阵.
图6的仿真曲线是利用3发3收系统得到,系统带有1个干扰源,干扰天线数为4,发射信噪比为20 dB,r和ri的取值如图所示.注:(a,b)=(r=a,ri=b).

图6 Ⅲ系统容量与IV系统容量的比较
由仿真结果图6可以看出:本文模型Ⅲ是相同信道模型下的容量下界,然而与更为一般的IV系统相比,容量的差别很小,尤其当信噪比很大时,两种模型可以相互等效.
4 结 论
在带有同信道干扰和协方差矩阵反馈情况下,提出了优化MIMO系统信道容量的传输方案.通过仿真发现在强干扰以及信道矩阵具有很强相关性的条件下文中所提出的方案可以接近最优传输方案.
带有同信道干扰的MIMO系统信道容量问题,理论研究难度很大,但却十分有实践意义.值得注意的是,目前涌现的理论相关的干扰对齐技术已在通信学界得到广泛关注[14].
附录A
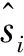
由文献[5],当M>N时,遍历容量的表达式可以写成如下形式:
(A1)
式中:
(A2)
{Φ2(k)}i,j=
(A3)
经过观察发现,式(A1)的分母部分与正文中式(14)具有相同的结构,所以不再重复关于分母部分的求导问题.
讨论式(A1)分子部分的求导问题.与正文讨论问题的方法类似,首先令
G2(k)=det(Φ2(k)),
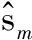
(A4)
式中:
{G2(k,r,m)}i,j=
(A5)
式(A5)包含的2个积分式可以参考正文中式(29)~(33)进行化简.
[1] GOLDSMITH A,JAFAR S A,JINDAL N,et al.Capacity limit of MIMO channels[J].IEEE Journal on Selected Areas in Communications, 2003,21(5):684-702.
[2] 闫秋娜,岳殿武,王 谦.同信道干扰下相关多输入多输出信道容量分析[J].电波科学学报,2012,27(3):556-563.
YAN Qiuna, YUE Dianwu,WANG Qian. Analysis of correlated MIMO channel capacity under co-channel interference[J].Chinese Journal of Radio Science,2012,27(3):556-563.(in Chinese)
[3] JAFAR S A,VISWANATH S,GOLDSMITH A.Channel capacity and beamforming for multiple transmit and receive antennas with covariance feedback[C]∥IEEE International Conference on Communications. Helsinki,2001,2266-2270.
[4] JORSWIECK E A,BOCHE H.channel capacity and capacity-range of beamforming in MIMO wireless systems under correlated fading with covariance feedback[J].IEEE Transactions on Wireless Communications,2004,3(5):1543-1553.
[5] KANG M, ALOUINI M S.Water-filling capacity and beamforming performance of MIMO systems with covariance feedback[C]∥4thIEEE Workshop on Signal Processing Advances in Wireless Communications. Rome,2003:556-560.
[6] LI J,ZHANG Q T.Transmitter optimization for correlated MISO fading channels with generic mean and covariance feedback[J].IEEE Transactions on Wireless Communications,2008,7(9):3312-3317.
[7] GOHARY R H,MESBAH W,DAVIDSON T N.Rate-optimal MIMO transmission with mean and covariance feedback at low SNRs[J].IEEE Transactions on Vehicular Technology,2009,58(7):3802-3807.
[8] GOHARY R H,DAVIDSON T N.On rate-optimal MIMO signalling with mean and covariance feedback[J].IEEE Transactions on Wireless Communications,2009,8(2):912-921.
[9] RAPPAPORT T S.无线通信原理与应用[M].北京:电子工业出版社,2004.
[10] YE S,BLUM R S.Some properties of the capacity of MIMO systems with co-channel interference[C]∥IEEE Internet Conference on Acoustics,Speech and Signal Processing. Philadelphia,2005,3:18-23.
[11] YE S,BLUM R S.Optimized signaling for MIMO interference systems with feedback[J].IEEE Transactions on Signal Processing, 2003,51(11):2839-2848.
[12] GRADSHTEYN I S,RYZHIK I M.Table of Integrals,Series,and Products[M]. 7thed. Orlando Academic Press,2007.
[13] ZHANG Q T, CUI X W.Outage probability for optimum combining of arbitrarily faded signals in the presence of correlated rayleigh interferers[J].IEEE Transactions on Vehicular Technology,2004,53(4):1043-1051.
[14] AYACH O E,PETERS S W,HEATH Jr.R W.The practical challenges of interference alignment[J].IEEE Wireless Communications,2013,20(1):35-42.
[15] BERTSEKAS D P.Nonlinear Programming[M].Belmont: Athena Scientific,1995.
[16] BOYD S,VANDENBERGHE L.Convex Optimization[M].Cambridge:Cambridge Univ Press,2003.
[17] ZHANG Q T,LIU D P.A simple capacity formula for diversity Rician channels[J].IEEE Communications Letters,2002,6(11):481-483.
[18] YUE D W,ZHANG Q T.Generic approach to the performance analysis of correlated transmit/receive diversity MIMO systems with/without co-channel interference[J].IEEE Transactions on Information Theory,2010,56(3):1147-1157.
[19] 王自力,龚耀寰.MIMO宏小区窄带信道模型的相关性能分析[J].电波科学学报,2005,20(1):37-42.
WANG Zili,GONG Yaohuan. Correlation oharacteristic analysis of MIMO macro-cell narrowband channel model[J].Chinese Journal of Radio Science, 2005, 20(1):37-42.(in Chinese)
[20] 李光球.相关衰落信道上MIMO系统中组合SC/MRC的性能分析[J].电波科学学报,2009,24(1):163-166.
LI Guangqiu. Performance analysis of combined transmit SC/receive MRC for MIMO systems in correlated fading channels[J].Chinese Journal of Radio Science,2009,24(1):163-166.(in Chinese)

