基于频谱监测传感网的分布式协同信号识别

吴 昊 柳永祥 姚富强 赵杭生

(1．解放军理工大学通信工程学院，江苏 南京 210007；2．南京电讯技术研究所，江苏 南京 210007；)

引 言

无线传感器网络具有监测精度高、系统容错性好以及可远程监控等特点，使得其在频谱监测领域具有广阔的应用前景.将传感器网络技术引入频谱监测领域，可为建立起全地域覆盖、全频域无缝隙、全时段不间断、全天候工作的电磁频谱监测网提供有力支撑.构建电磁频谱监测传感网可为需用频的设备提供可用的频率指配，为正在用频的设备提供干扰源检测、测向、定位、跟踪、识别分类能力，为重要设备的用频参数提供安全保密支持.要实现频谱监测传感网从理论走向实用化，服务于频谱安全领域、公众服务领域，必须首先突破分布式协同频谱感知关键技术，为提高频谱监测传感网的信号检测能力、参数提取能力、调制识别能力提供技术支撑和方法.文中充分借鉴国内外现有的分布式信号协同检测、识别分类的理论和最新研究成果，重点解决频谱监测传感网中的分布式协同信号识别技术.

目前多数调制识别技术[1-7]是基于单节点完成的，主要是基于假设检验和统计模式识别的两类方法.但是单节点受环境变化的影响，容错性能较差，从而导致其信号识别率较低，此外，随着作战地域或通信范围不断扩大，单节点的监测能力以及对信息的实时处理能力都将受到极大限制.而基于无线传感网的分布式信号识别技术，能够利用数据融合[8]，消除对未知信号判断模糊性，提高识别准确率.

1 分类特征建立

第i个传感器节点在平坦衰落环境中，接收到的受噪声污染的信号可表示为[9]

(1)

式中：A是接收信号的平均功率；az为发送码元序列；p(t-zTs)是发送码元波形，Ts为符号周期；ωc为载波频率；θc为载波相位. 假设所有ni(t)为零均值的复高斯白噪声，且方差为N0，假设E[|az|2]=1，则信噪比可定义为RSN=A/N0.

完成对接收信号yi(t)的预处理，即完成载波、相位、定时同步以及波形恢复，得到复包络基带信号为

(2)

式中，Δθ为相位抖动.

利用各阶累积量对2ASK、4ASK、BPSK、QPSK、16QAM、2FSK、4FSK、8PSK、MSK等常见调制信号进行分析，得到如表1所示的数字调制信号各阶累积理论值.通过对各阶累积量理论值分析，可建立如下特征参数：

(3)

首先利用特征向量{T1,T2}可将待识别的调制信号分为三大类：当{T1,T2}={1,1}时对应的数字调制信号为{2ASK/BPSK、4ASK}；当{T1,T2}={1,0}时对应的数字调制信号为{QPSK/16QAM}；当{T1,T2}={0,0}时对应的数字调制信号为{2FSK、4FSK、8PSK、MSK}.

其次，利用特征参数T3与T4进一步分类: 对于{2ASK/BPSK、4ASK}，当T3=2对应的是2ASK/BPSK，当T3=1.36对应的是4ASK；对于{QPSK/16QAM}，当T4=16对应的是QPSK，当T4=13.76对应的是16QAM.

利用信号功率和平方谱线特征对{2FSK，4FSK，8PSK，MSK}这一类数字调制信号进行分类识别.图1和图2所示的是2FSK、4FSK、8PSK、MSK功率谱和平方谱，从图中可知，通过搜索调制信号功率谱和平方谱的谱峰数可对这类信号进行分类，假定功率谱谱峰用P1表示，平方谱谱峰用P2表示，信号功率谱反映调制信号的功率分布，如{2FSK、MSK}为单谱峰信号，频谱较为平坦，而4FSK频谱起伏较多，而8PSK的谱形状完全不同于其他类，因此通过合理设定门限值，利用P1可将这类信号分为4FSK、8PSK、{2FSK、MSK}三类；进而采用P2可将2FSK与MSK区分开，由于倍频后，2FSK在传空号频率处出现离线谱线，而MSK没有，利用P2可将MSK从2FSK中检测出来.

在高斯噪声信道下，功率谱谱峰P1可在信噪比为-15 dB的情况下保持良好的健壮性，此时8PSK谱形状完全被噪声淹没，虽然仍可根据其它几类信号的谱峰特征将其区分开，但随着信噪比的继续降低，P1特征将急速恶化，无法更好的进行分类识别.而平方谱谱峰P2可在信噪比为-4.5 dB时保持较好的健壮性，但随着信噪比的继续降低，2FSK在传空号频率处出现离线谱线将被噪声淹没，无法将其与MSK区分开.

因此，传感器节点建立的用于各类调制信号识别的分类特征向量为

T={T1,T2,T3,T4,P1,P2}，

(4)

利用其相互组合可得到较好的识别概率.

表1 数字调制信号各阶累积理论值

图1 2FSK，4FSK，8PSK，MSK的归一化功率谱线

图2 2FSK，4FSK，8PSK，MSK的归一化平方谱线

2 信噪比盲估计

第1节完成了传感器节点对数字调制信号特征参数提取和分类特征向量的建立，在频谱监测传感网的融合中心上，还需要对各传感器节点分配权值，即融合中心对传感器节点的信任度进行赋值.下面利用信噪比的大小对其分配权值.

第i个传感器节点的接收信号可表示为式(2),进行无失真采样后，得到其离散形式为

yi(k)=si(k)+ni(k)，k∈[1,2,…,N]．

(5)

式中：si(k)表示调制信号；ni(k)为独立的零均值高斯噪声；N为采集信号长度.构造接收信号的协方差矩阵[10-11]，令

l,q∈[1,2,…,m]，

(6)

则协方差矩阵的模型为

(7)

式中，m为协方差矩阵的维数，它影响协方差矩阵及其奇异值表述信号的分辨率，m选择过小，协方差矩阵失真大，影响信噪比估计，m选择过大，增加不必要的计算量，m一般取值为50～100.

对接收信号的协方差矩阵分解为

R=E{yyH}=E{[s+n][s+n]H}

=E{ssH}+E{nnH}=Rs+Rn，

(8)

由于观测噪声与信号相互独立不相关，且具有相同的方差，所以Rn=σ2I，则式(8)可变为

R=Rs+σ2I.

(9)

若rank(Rs)=r,则：

R=U∑UH+σ2I=U(∑+σ2)UH=UΠUH.

(10)

式中，

Π=∑+σ2I

(11)

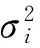
由式(10)可知只要得到接收信号的信号子空间的维数，即可分离出信号子空间和噪声子空间，目前估计信号子空间的方法有最小描述长度(Minimum description length,MDL)、Akaike信息量准则(Akaike information criterion, AIC)、联合信息准则(Combined information criterion,CIC等方法，这里采用MDL方法，具体准则如下：

(12)

定义MDL目标函数为

FMDL(p)= (N-m)(m-p)lg[Tsph(p)]+

(13)

信号空间的维数估计为

(14)

根据上述原理，给出具体信噪比估计步骤如下：

1) 根据式(6)与(7)构造协方差矩阵；

为检验算法有效性，计算估计偏差和标准差作为评估方法，定义如下：

(15)

(16)

利用所提出算法对QPSK、16QAM两种信号的信噪比估计进行仿真验证，结合式(15)和(16)对性能进行分析，假定协方差矩阵的维度为60，对两种信号进行1 000个码元的采集，仿真次数为100次，信噪比变化范围为-8～20 dB.

图3给出了两种信号信噪比估计的偏差和标准差随信噪比的变化曲线.由图3可以看出: 算法在信噪比小于13 dB时，偏差能够控制在0.5 dB范围以内; 而标准差可保持在0.25 dB以内；在信噪比较大时，偏差较大; 但当信噪比较大时，偏差对信号识别概率的影响几乎可以忽略.所以，提出的信噪比算法满足对QPSK、16QAM两种信号识别的要求.

图3 信噪比估计的偏差和标准差

3 分布式协同信号识别框架

上面详细介绍了频谱监测传感网中传感器节点上完成的特征参数提取与信噪比盲估计，为进一步提高对信号的识别概率，利用数据融合，可极大程度消除对未知信号判断模糊性，当少数传感器节点信道条件恶化时，融合中心仍能保持较高的识别概率.目前，关于多传感器信号识别的融合算法主要是在决策层上采用大数判决的方法[12]，即根据传感器节点的判决信息，选择多数传感器都判断的类型作为最终识别结果.而文中提出的方法是根据对各传感器节点信噪比的估计对其可信度进行赋值，在特征层上，将各传感器节点提取的特征向量进行融合，利用融合后的特征向量进行信号调制方式识别，从而完成整个分布式算法的识别过程.图4给出了分布式协同信号识别整体框架.

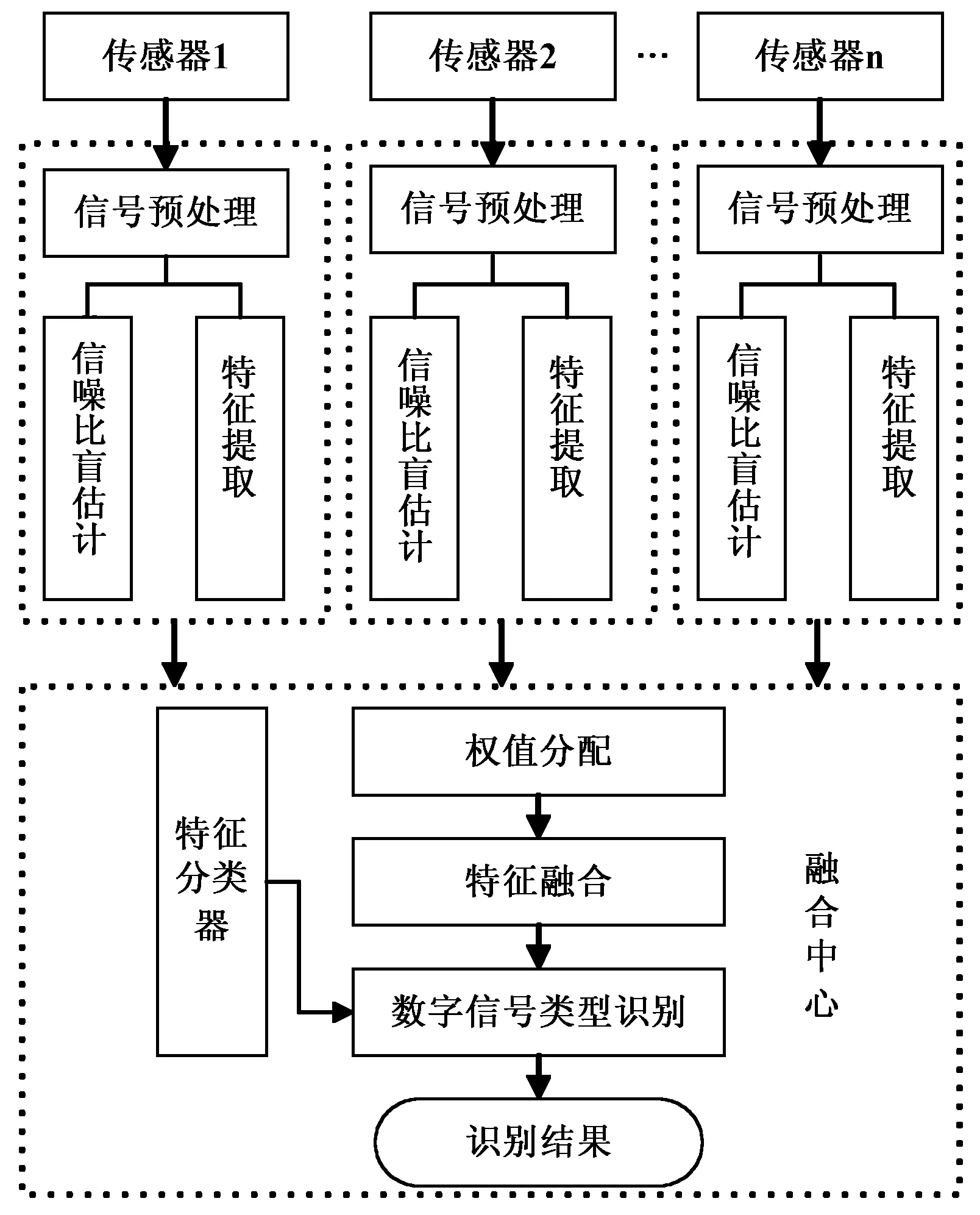
图4 分布式协同信号识别框架

其具体实施步骤为：

步骤1 信号预处理：对各传感器节点采集的信号数据进行预处理，如完成载波、相位、定时同步以及波形恢复，得到待识别的复基带调制信号.

步骤2 特征提取：根据第2节所述，各传感器节点提取用于调制识别的各类特征参数，这里主要提取特征向量T={T1,T2,T3,T4,P1,P2}.

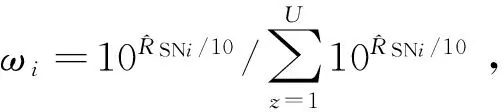
步骤6 类型识别:根据第2节所建立的特征分类过程，结合步骤5融合后的特征参数，进行数字调制信号的类型识别.

4 仿真分析

仿真场景1 假设传感器节点数目为10，且所有传感器节点的接收条件相同，信噪比在-5.5～-3.5 dB变化，仿真次数为100次，信号采样频率为20 kHz，码元速率为100 bit/s，且MFSK的频偏为500 Hz，相位抖动为5°，仿真采样码元为2 000个，噪声为高斯白噪声.融合算法对各种调制信号的识别性能如图5所示，当信噪比大于-4.5 dB时对所有数字调制信号均能达到90%的识别概率.

图5 10个接收条件相同传感器的识别概率

仿真场景2 当传感器节点数目为3个，且接收条件不同，即其中一个传感器节点的信噪比RSN1变化范围是-8～0 dB，另外两个传感器节点的信噪比分别为RSN2=RSN1+1，RSN3=RSN2+2，其他仿真条件与场景1相同，图6给出了融合算法对各种调制信号的识别性能，在信噪比大于-5 dB时能达到90%的识别概率.该仿真场景主要体现的是当个别节点所处接收信号条件相对恶劣的情况下，只要保证其他某几个节点的接收环境，经过融合中心的融合处理，仍能达到较高的识别概率.

图6 3个接收条件不同传感器的识别概率

5 结 论

研究了一种分布式协同信号识别方法，对于单传感器节点采用高阶累量和谱线特征建立了一组健壮性较强的分类特征，节点将信噪比的估计值和特征参数作为样本，在特征层上，根据信噪比为每个传感器分配权值，并对各传感器节点的特征向量进行融合，最终得到能够反映单传感器节点不确定性的融合特征向量，结合已建立的分类算法对接收信号进行最终判别.仿真表明，即使在部分传感器节点的接收环境较为恶劣的情况下，该方法仍能保持较高的识别概率.

[1] 杨 琳.数字通信信号调制方式自动识别技术研究[D].合肥: 中国科学技术大学,2008.

YANG Lin. Research on Techniques in automatic Modulation Classification for Digital Communication Signals[D].Hefei: University of Science and Technology of China,2008.(in Chinese)

[2] 冯 祥,李建东.调制识别算法及性能分析[J].电波科学学报,2005,20(6):737-740.

Feng Xiang,LI Jiandong. Modulation classification algorithms and performance analysis[J].Chinese Journal of radio science,2005,20(6):737-740.(in Chinese)

[3] 胡建伟,杨绍权,汤建龙.多径信道下MPSK信号的调制分类算法[J].电波科学学报,2005,20(4):505-509.

HU Jianwei,YANG Shaoquan,TANG Jianlong. Modulation classification of MPSK signals in multipath fading channel[J]. Chinese Journal of Radio Science,2005,20(4):505-509.(in Chinese)

[4] 李 鹏,汪芙平,王赞基.一种短波信道中数字调制方式识别算法[J].电波科学学报,2007,22(5):735-739.

LI Peng,WANG Fuping,WANG Zanji. Algorithm for modulation recognition in shortwave channel environment [J]. Chinese Journal of Radio Science,2007,22(5): 735-739.(in Chinese)

[5] 范海波,杨志俊,曹志刚. 卫星通信常用调制方式的自动识别[J].通信学报,2004,25(1):140-149.

FAN Haibo,YANG Zhijun,CAO Zhigang. Automatic recognition for common used modulations in satellite communication[J].Joural of China institution of communication, 2004,25(1):140-149.(in Chinese)

[6] WEI W, MENDEL M.Maximum-likelihood classification for digital amplitude-phase modulations[J].IEEE Trans on Communication,2000,48(2):189-193.

[7] 黄 英,雷 菁.卫星通信中调制识别算法研究[J].系统工程与电子技术,2009,31(6):1303-1306.

HUANG Ying,LEI Jing.Research on recognition of modulation signals in satellite communication [J]. Systems Engineering and Electronics,2009,31(6):1303-1306.(in Chinese)

[8] 韩崇昭,朱洪艳,段战胜.多源信息融合 [M]. 2版.北京: 清华大学出版社,2010:1-12.

[9] ANANTHRAM S, BRIAN M S.Hierarchical digital modulation classification using cumulants[J].IEEE Transaction on Communication,2000,48(3):416-429.

[10] ZHAN Yafeng,CAO Zhigang,MA Zhengxin. A blind SNR estimation algorithm for MPSK signals in AWGN Channel[C]∥Proceedings of ICFS. Tokyo: Waseda University,2002.

[11] 孙刚灿,安建平,杨 杰,等.非协作通信中的信噪比估计算法[J].北京理工大学学报,2009,29(8):708-712.

SUN Gangcan, An Jianping,YANG Jie,et al. Signal and noise ratio estimation method in non-cooperative communication[J].Transactions of Beijing Institute of Technology,2009,29(8):708-712.(in Chinese)

[12] 程汉文,陈 亮,吴乐南.基于加权表决的决策层融合多系统调制识别[J]. 系统工程与电子技术,2010,32(2): 342-345.

CHENG Hanwen, CHEN Liang, WU Lenan. Weighted voting based on decision fusion for modulation classification of multisystems[J]. Systems Engineering and Electronics,2010,32(2): 342-345.(in Chinese)