应用hLDA进行多文档主题建模关键因素研究

衡 伟，于 佳，李 蕾，刘咏彬

(北京邮电大学 计算机学院 智能科学技术中心，北京 100876)

1 引言

为了从数据中学习层次信息，Blei等人[1]提出了基于nCRP的层次潜在狄利克雷分配(以下简称hLDA)非参模型。模拟数据和JACM语料的实验评估证明了其具有非常好的效果[2]。Asli和Dilek等人[3]采用交叉验证的方法对hLDA进行英文多文档摘要建模，效果显著。刘等[4]利用hLDA进行中文多文档聚类和摘要的研究，亦取得了非常好的效果。

但hLDA的建模效果却因语料和应用建模者的不同而差异巨大。虽然在Blei的论文中提出了无监督的、针对先验超参的MH抽样方法[5]，在迭代尽可能多的条件下，理论上可以实现完备的后验推理[6]。但是，实际应用中资源有限，我们无法保证进行足够多次的迭代，且不同的语料特征以及建模需求使得迭代次数具有很大的不确定性；加之吉布斯后验推理算法是一种随机算法，每次迭代稳定的状态都不同[7]；再者，应用中对最优树结构的评估方法也有较大的不确定性。一定程度上需要通过多次局部最优的结果来逼近全局最优。Blei仅仅给出了模型参数本身[2]，却没有详细的分析参数选择过程。同样Asli和Dilek的交叉检验寻找模型参数方法则过多的限制了模型的泛化效果。本文通过统一分析框架，采用理论分析与实验相结合的方式，对应用hLDA到多文档主题建模任务中的关键影响因素进行深入研究，试图寻找优化的建模策略、建模流程以及有效的参数配置方法，能在有限资源、有限迭代、语料多变的情况下，尽可能让建模结果更好地逼近全局最优，从而为hLDA实现高效的层次主题建模提供有益的参考。

文章结构安排如下： 第2节介绍统一分析框架，从贝叶斯线索和范围线索两个角度分析多种影响因子，同时简要介绍了实验模块；第3节针对 hLDA 模型文档生成过程的超参进行分析和实验；第4节给出了吉布斯抽样算法后验推理的关键影响因素；第5节针对影响建模的全局因子进行了分析；第6节给出一个经验型优化建模流程，并结合最新的ACL MultiLing 2013多语言多文档摘要数据进行建模效果实验与效果评估。

2 统一分析框架及实验模块

2.1 统一分析框架

如图1所示，黑色矩形虚线表示范围线索，在虚线框之外是一些全局的建模影响因子，如抽样与否、树的深度、语料的大小，词汇量等特征。虚线内部是贝叶斯线索的影响因子，如狄利克雷(Dirichlet*为了与Blei论文中表示一致，后面我们将使用Dir()表示。())分布超参η、 GEM分布超参m, π、nCRP过程超参γ*此处表示同Blei hlda算法包[http://www.cs.princeton.edu/～blei/topicmodeling.html]中参数命名。。黑色椭圆形实线是贝叶斯过程： 黑色有向实线箭头所示为基于先验的文档生成过程。逆向的黑色虚线箭头即贝叶斯后验推理： 从语料出发*忽略了预处理到生成文档到词的过程，图中的Doc, Wd,n也应该有相应的黑色虚线表示。，选择路径Cd和词Wd,n，获得最优树结构。

图1 统一分析框架

从图1的统一分析框架，我们能够窥见hLDA模型算法的全貌，从而有利于深入分析建模影响因子。后面三节便是以这两个线索为纲展开的，并结合具体的实验分析，为此，我们对用于建模分析的实验系统做一个较为全面的介绍。

2.2 实验系统介绍

2.2.1 实验系统框架

实验系统由三个模块组成： 预处理、hLDA建模、结果分析评估。如图2所示。预处理模块对语料进行分句、分词、生成词表、统计词频特征等。生成hLDA建模输入文件，同时为hLDA超参选择提供分析依据。hLDA建模是核心模块， 其设置文件中的超参选择是建模的重点，主要依据语料本身的特征分析以及对于建模结果分析的反馈。结果分析评估模块是实验分析的基础，从而验证各个建模影响因素。

图2 试验系统框架图

2.2.2 实验语料来源

实验语料来源于两部分： 其一收集了国内门户网站新闻报道，共十个话题，每个话题10篇相关报道，即Portal News。便于图表叙述，给出了英文缩写，如甘肃校车事故(SBAG)，伊朗制裁(IRSA)等。其二是ACL MultiLing 2013多语言多文档摘要评测发布的数据，也由十个话题，每个话题下10篇新闻组成： 如印度洋海啸(M000)，伦敦爆炸案(M001)等。

3 文档生成过程

3.1 嵌套中国餐馆过程nCRP

nCRP是hLDA的核心，属于贝叶斯非参建模家族，近些年在层次主题建模领域受到了广泛的关注[8-10]。nCRP构造了一个树状层次结构先验，超参γ决定先验树结构的形状，即每个文档每一层的路径选择。称之为嵌套中国餐馆过程是因为本质上它只是对于每一层都使用中国餐馆模型(即CRP)进行路径选择。

3.1.1 中国餐馆过程CRP

CRP可被简单表述为如何从以下等式的条件概率函数中选择一个样本所属的类别聚簇，见式(1)。

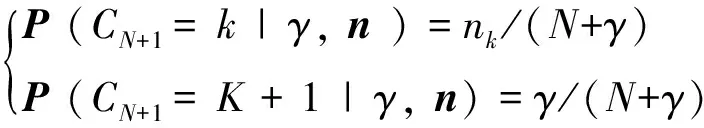
(1)

其中，N表示已有的样本数，CN+1表示新来的样本，K表示目前的样本类别数，nk表示第k个样本类别所含有的样本数目，n表示所有nk所组成的集合向量。可以看出，某一个类别上的样本越多，则新抽样本属于该类别的概率越大。最终聚簇数的期望如式(2)所示。

在给定γ的情况下，占用聚簇数的期望随着样本数n呈指数增长，因此，可以通过分析文档数目和期望的聚簇数来反向估计γ的范围。这在实际的分析nCRP超参的过程中亦具有较高的参考意义。

3.1.2 nCRP及γ值实验分析

CRP是一个在整型离散空间上的随机过程，nCRP同样是一个随机过程，但不是在一维的整型空间，而是在树的深度维度上的整型向量空间。因此，当假设每个聚簇上有一个潜在主题变量βk时，某一条聚簇路径上也有一个潜在向量<β0,kβ…,kβl,k>。nCRP过程指定了文档所属的潜在向量聚簇。对于三层树结构，nCRP过程相当于在一个三维整型空间中去选择聚簇，每个样本则是三维空间中的某一个点。

如表1所示，实验分析在同一个话题语料*ACL MultiLing 2013中文语料下的M004话题。下，γ值所引起的聚簇数(即路径数)的变化。

表1 GAMMA值对聚簇数和词层分配影响

当γ=0.2时，前段主要路径聚集，而路径数却相应的减少。随着γ值从1.0变化到8.0，各聚簇分布逐渐趋向平均，且路径数也在相应增加。各层词分配在随机抽样允许的变动范围内，比例基本不变。从原理上分析，如式(1)所示，γ值增大使得选择新聚簇的可能性增加，在总文档数不变时，原本过于聚集的簇倾向于分散，产生更多新聚簇。而第三层词的分配是随着γ的增大而减少，而最后的路径数却呈现增多的趋势，其原因便在于，γ增大的过程中，从根节点到叶子节点各个层次聚簇数都相应的增加，由式(2)可知，文档数越大，词数越多的情况，聚簇的增加越快，因此相对而言，根节点增加的要比叶子节点快，为了满足这样的先验假设，后验词分配便逐渐的从叶子往根聚集，从而导致叶子节点词的减少。

3.2 折棒构造

折棒构造是狄利克雷过程(以下简称DP过程)的另一种构造方式，侧重于以最终分布为中心的构造。每次折棒，都会通过Beta分布得到最终分布比例的一部分，而CRP每次抽样只是对最终分布比例的一次更新，随着抽样次数的增加进而愈加接近最终分布。关于折棒过程更为详细的叙述，很多论文中皆可参考[3-4，8，10]。既然CRP和折棒过程都是DP过程的不同构造方式，对于CRP的理论分析同样适用于折棒过程，如最终聚簇的期望等。

3.2.1 参数m和π实验分析

参数m控制着从根节点到叶子节点的分配比例，而π则指定该分配比例的严格程度，但相对m，其影响要小。实验首先从Portal News语料中随机选取两篇，分析m从0.25到0.75变化时词的分配。如图3所示，上下各三个饼状比例图，分别表示一个主题在不同的m值条件下，树中各层词分配比例。饼状图中的黑色部分表示第三层叶子节点所占词的比例，白色部分表示中间层词所占据的比例，而灰色部分则表示根节点词所占的比例。

图3 不同m下，三层树结构时词的分配比例

从第一行三个饼状图的比例变化可以看出，随着m值的变大，叶子节点中词的比例明显增加，而根节点中词所占的比例则在减少。第二行虽然不同语料差异使得各层词的比例不完全相同，但是这种趋势也非常显著。可以推测，m越大，文档中的词越向叶子节点聚集，越倾向于较为具体的主题，反之亦然。

接着图3的分析，利用ACL MultiLing 2013中前五个主题的语料，分析确定m值情况下，词分配比例的稳定性。如表2所示，随着m从0.25增加到0.75的过程中，level0层的分配比例在逐渐减小,level2层的比例在逐渐增加。从原理上来看，折棒构造过程中m、π的先验影响效果比较明显，尤其在树的层数小、主题下文档数较少时，贝叶斯后验解释受先验的影响较大。因此，在应用建模时可以根据期望的主题层次分布和抽象具体词的比例来确定m值的范围。以此类推，结合CRP中的理论分析和实验评估，我们可以给出一个经验化的比例范围，从而有利于我们所期望的更为精确的m值控制。

接着前面在nCRP试验中的分析， 当γ产生较大变化时，对于路径树和聚簇比例的变化有一定的影响， 但是各个层次词的分配比例受到γ参数的影响较小。这在一定程度上为我们细化γ和m参数对树结构的调节范围提供了可能。

表2 不同语料数据时，确定m值下各词层分配的稳定性

3.3 狄利克雷分布和DP过程

狄利克雷分布决定了每个节点上主题先验βk。文档生成过程中，首先假设一个无限深度和无限宽度的树结构，树中的每一个节点以超参η生成一个主题，以此进行嵌套中国餐馆过程和折棒过程的构造。两种构造却已经不仅仅是由样本数N和先验超参γ或m、π控制，在单纯的整型空间上的聚簇划分。因为每个节点都有了实际意义，即主题βk。于是这两种过程都变成了在潜在主题变量下的混合模型。我们首先分析DP的形式化定义以及DP的两种构造过程，以此为切入点来分析狄利克雷分布所确定的主题和这两个构造过程的关系。

3.3.1 从DP的角度分析文档生成过程

DP是一种随机概率测量在一个可测量空间上的分布[11]。在生成主题节点值空间的Dir()分布的基础上，分别把nCRP和GEM的构造过程理解成为一种DP过程。对于nCRP而言：

式(3)中，L表示的是嵌套的层数向量所构成的分布矩阵，对于每一层通过CRP过程，得到一个比例分布，结合层数得到这样一个矩阵结构。接下来对一篇文档从L矩阵中的第一行开始一直到结束，逐步选择相应的基分布值，即β向量，其向量长度等于嵌套的次数，也即树的深度。Categorical(K)分布表示从某一有K个结果的随机事件中抽样。这便是通过嵌套CRP方式构造一个DP过程。而式(4)中，则是直接从DP定义的概率测量的角度来生成。好处在于能够直接清晰的分析出狄利克雷分布作为基分布在整个nCRP过程中的作用。而对于GEM而言，其基分布则是前面nCRP所形成的β向量的分布，然后对于向量的维度即同样树的深度L，进行折棒构造，如式(5)，(6)所示。

从以上的分析我们不难理解，对于基分布狄利克雷而言，nCRP过程类似于一种对每一层取值空间进行了扩展组合，然后在一个高维的更大的空间内进行向量选择，在此基础上，GEM分布再对已选的向量进行每一维度上的概率选择，从而产生相应的词。

3.3.2 参数η实验

如表3所示，我们分析在叶子节点上的η值(其余两层值分别为5.2/0.025)变化时，相应的主题路径以及各节点上文档和词的变化。

表3 η对树结构的影响

其中，第一列是叶子节点上的η值，第二列是从根节点到叶子节点总的词分配，第三列是总的路径数，剩下的五列表示最主要的五个路径上文档和词分配。当η为0.05和0.005时，叶子节点的词分别为582和564，在一定抽样不确定性允许的情况下，词数是相对稳定的，叶子节点上总路径数变多，各个路径上文档和词的数量则变小。随着叶子节点η的迅速变小，其词由上往下流动，前面两层的路径数变小，下层的路径数相对变多，嵌套的效果使得整体路径数变小。因此η对于词的分配、路径数有很大影响。且往往在与GEM_MEAN(m)参数混合作用的情况下，这种影响会导致在实际建模中一些意想不到的问题，最经典的则是mode.levels文件的缺失。

4 后验推理

4.1 吉布斯抽样

吉布斯(Gibbs)抽样广泛应用于统计推理领域，尤其是贝叶斯后验推理。主要通过构造一个蒙特卡罗马尔科夫链使得其稳定状态分布等于后验分布[2]。实际应用中如何评估马尔科夫链的收敛性往往决定着推理的效果。而迭代次数的设定对链的收敛有着很大的影响。

通过Gibbs抽样算法，在无限次迭代达到收敛时，可以实现对语料理想的建模。但正如我们在第1节所讨论的，往往受限于实际应用瓶颈。因此，在前面参数调节的基础上，我们首先通过初始参数设定，对目标语料形成了一个较为理想的层次分类，然后分析在增加迭代次数的条件下，各个层次主题的变化。在m和π参数不变的情况下(m=0.5, π=100)，观察迭代次数对词层分配的影响，如表4所示。

表4 迭代次数对于词层次分布的影响

在此迭代条件下，可以发现迭代次数对于词分布影响很小，马尔科夫链已经达到稳定的局部收敛状态，因此，我们可以从词层的稳定性上来判断链的收敛情况。但是，对于不同特征的语料，不同迭代次数下迭代收敛和路径数却是不同的，如图4所示。

图4 不同迭代次数下路径数比较

横坐标为话题，纵坐标为最终的路径数。在其他参数一定的情况下，迭代次数越大，得分最高的mode所形成的最优路径便会越逼近实际主题中的真实路径。从图4中可以看出，在考虑到随机算法的不确定性影响的情况下，这种变化趋势基本上是保持一致的。一般可以分为两种情况，第一种如主题4，5，7，9，10，路径数随着迭代次数增加，成一致的变化趋势，说明通常在给定语料大小条件下，随着迭代次数的增加，最终路径数会趋向于一致的状态。而对于主题如1，2，3的路径数则表明在目前迭代情况下，树的路径已经趋向于一种较为稳定的变化状态，这恰恰是我们抽样最优树结构的基础。但也有较为不一致的情况，如主题8，由于其语料特征的差异使得在实验的10 000到100 000次的迭代范围之内，路径数不稳定，并没有达到一个较为稳定的状态，因而三组实验时路径数变化很大。

还有一种情况，在一定的迭代范围内，路径树已经趋向于稳定状态，但可能陷入一种局部最优的稳定状态。对此，我们不可能通过无限制的增加迭代次数来最优化，通常通过多次重启抽样，或是改变抽样中的随机延迟值*详情见Bleihlda算法包[http://www.cs.1rinQton.edu/～blei/topicmobdeling.html]中源码实现。(SHUFFLE_LAG)或是抽样延迟值(SAMPLE_LAG)。模型本身的超参很多，加之随着文档数的增加带来链上变量的急速增长，随机条件下通过有限的迭代，很难有较好的效果。因此，相比于这种概率随机条件，启发式的逼近调节效果往往更为显著。

5 全局建模策略

5.1 树的深度

深度假设是hLDA一个最基本的假设，也反映了主题建模粒度的期望。我们给出了不同树深度条件下，Portal News中的8个话题平均路径数变化，如表5所示。

表5 不同深度情况下的平均路径树变化

随着树深度的增长，路径数呈现快速增长的趋势。与其他超参对于路径数的影响比较，其增长趋势是最快的。由此分析，在设定超参时，树的路径树是我们首先需要考虑的参数。结合原理分析，我们知道hLDA的核心是基于nCRP的先验树结构，不管是对于文档生成的路径选择还是每个节点的主题分配，首先需要对深度做假设，树越深则CRP的嵌套效果越明显，GEM分布层次的后验性越强。同时主题层次越多，每次运行的稳定性越差。

5.2 超参抽样与否

超参抽样的目的是为了尽可能的减少手工设定超参对于最终文档树结构的影响[12]，使得实验结果来源于语料本身特征。但是抽样也同样存在一些缺点，首先其限制了我们对于超参更为灵活的、目的性的调整；其次，从算法的效率考虑，抽样情况下的时间复杂度要高出许多。抽样超参的选择主要集中在主题βk的超参η，词分配超参m和π。我们从语料中随机选择四个主题，进行抽样影响因素的分析，如图5所示。

图5中分析了不抽样，抽样η(ETA)，抽样m,π(GEM)和两者都抽样时，四个话题路径数的变化。一方面对于不同的抽样选择， 四个话题最终的文档路径数变化趋势是一致的，对于抽样η和不抽样η的情况，路径数变化尤其的大，相比之下GEM参数的抽样要小点。结合3.3.1节的分析，η是nCRP过程中的基分布，控制着节点的主题，最直接的反映了文档的后验解释。另一方面，在对其选择抽样时，相比于GEM参数m的0-1的取值区间，其可以在整个实数范围内取值，因此随机化的区间更大，在一定的迭代次数下，并不一定能保证逼近最优值，因此对于整个路径数的影响比GEM的变化更大。

图5 不同超参的抽样情况下的路径树变化

5.3 语料特征

如表6所示，仍然从Portal News语料中随机选择四个话题，统计每个话题下的句子数、总词数、词表大小，以及相应的人工专家进行主题摘要归纳的主题数。

表6 语料大小与词表统计

对表6中词频特征按照文档中词的出现顺序进行了统计，以尽可能保证文档中词分布特点的同时，保留住其出现的上下文特征*主要是词的前后关联顺序不变，有利于我们分析相同词频下相似词的聚集。，如图6所示。

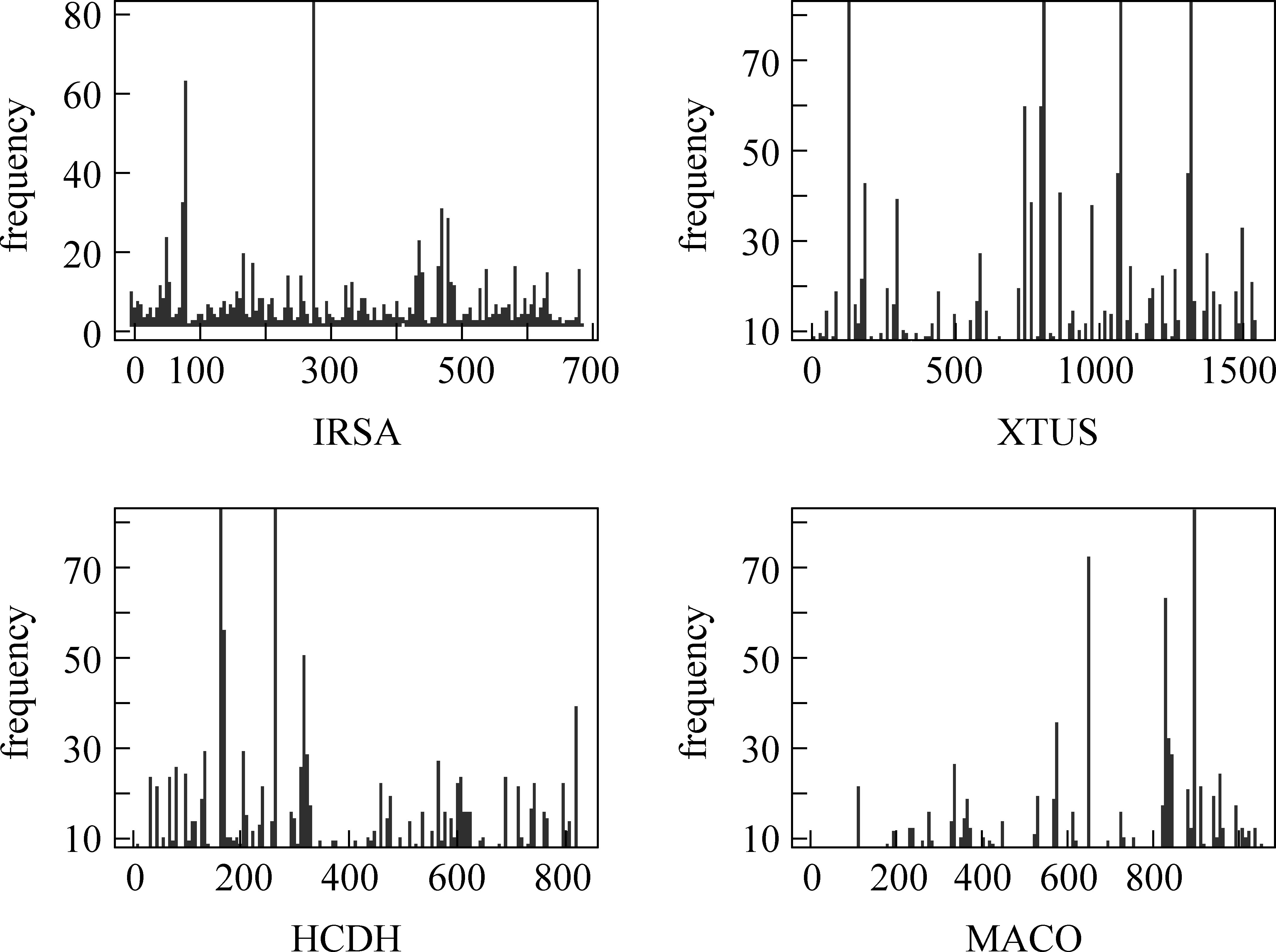
图6 四个话题词频分布特征

结合表6和图6来分析语料特征因素对潜在主题数目的影响。如第二个IRSA话题，词汇量、总词数相对较少，占据词汇量大部分的主题出现的便会少；再根据图6中的词频分布情况，只有三个较为明显的突出部分。与之作为对比的则可以看话题HCDH，首先句子数目，词汇量以及词表都比较大，但是我们发现其主题也比较少，结合词频特征，其词频高的也比较多，但为何主题数比像IRSA中的还要少，原因在于很多词的词频都比较高，但是这些较高的词频往往同时出现，且是关于某个特定的话题，即词之间上下文相关度比较高。

6 建模流程及效果评估

6.1 经验化建模流程

基于全局和局部因子的统一分析，本文给出一个实际建模应用中的经验化建模流程。

1) 产生hLDA模型的输入文件以及分析语料中的特征信息。

做必要的预处理工作产生hLDA模型的输入文件，同时分析语料的特征信息，如每个话题下文档的大小、词汇量、词频分布、关联度等统计特征。

2) 评估待建模树结构的深度。

结合语料规模、高频词语义相似度，以及建模目标等，来最终确定主题建模的深度。一般而言，树的深度至少为三层，且树层数越深，后验推理越复杂，所需的迭代次数也越多，在这最终得到最优结果的稳定性也越差。

3) 是否选择抽样超参。

后验推理的核心过程便是迭代最优化，因此在足够多次迭代下，往往抽样是较好的选择，但对于hLDA抽样初始值的选择还没有较为成熟的算法指导，对于一般建模者而言，随机初始化抽样往往不能取得较好的效果。经验表明，一般在两种情况下，我们采取抽样超参的策略。首先， 在人工设定超参的情况下，如果建模这对于各个因素的影响不清楚。其二，对于运行结果我们不满意，可以通过抽样来确定一个近似的范围，其后在进行人工设置。在抽样超参时应当尽可能增加超参的迭代次数。

4) 每一层的主题参数η。

我们注意到如果η太大了(如η> 8.0)，后验的节点聚集便会很大，相应的路径数便会变得非常少，反之亦然。同时，我们还应该考虑到最后马尔科夫链的收敛性，对于η的先验评估应该尽可能的与下面GEM参数的调节趋势一致，否则可能导致在迭代次数内评估最优mode的失败。

5) 路径词分配的m,π参数。

后验解释倾向于把一般的词放在根节点，具体的词在叶子节点。因此，根据树的深度对m进行设置，一般三层或四层的情况如图3和表2中所示的那样，0.75已经是很大的值了，其将直接影响词的层次分配和前面η参数的调节效果。

6) 非叶子层上的nCRP参数γ：

由公式(2)我们知道随着语料数量大小的增加，每一层聚簇数目的期望是呈现log增长的趋势，同时在表1中我们给出了聚簇数和γ之间的关系。我们可以再此基础上相应的较为准确的评估γ的超参设置。

7) 树结构先验的参数：

一个重要的参数便是SCALING_SHAPE，其直接影响着树的形状。通过对它的调节来对抽样的效果进行修正。参数SCALING_SCAL控制着树的规模比例大小。通常我们在对其形状先验预设的基础上，再来调节它。

基于以上建模流程，我们参照2.2.1节的框架图进行具体语料超参的设置，顺序建模和部分的循环修正，最终实现最优效果。

6.2 实验及效果评估

我们对Portal News语料下的十个话题进行了实验，在三次修正后，对hLDA建模结果和人工总结的结果进行了比较，实验中树的层次为3，如表7 所示。

表7 建模结果与评估得分

续表

themelevel#1level#2hLDA#1hLDA#2scoreHCDH574．8104CQWF495．3105SBAG4106105GBAB684．8113LTFC6147．2125MACO476．784ROHN59794

其中分数主要分为五个等级，从1(差)到5(非常好)。从十个话题的实际建模效果来看，平均都在4(好)等级左右。接下来我们又选择了ACL MultiLing 2013语料下的巴厘气候会议(M004)话题，对比抽样建模(10万次迭代)、随机建模结果以及本文提出的基于分析框架下的建模，给出一个可视化的建模树结构，每个树节点就是一个主题，我们选取了每个主题上高频词来反映这个主题的特征，如果某个主题节点上词数太少则为了树结构的展现效果，我们会用其父节点上的词填充。

如图7所示，整体上来看，两者树结构显得比较单一、少分支，这反映出了建模聚类结构过分的聚集在前面主要路径上，这不符合我们实际语料中子主题的特点。对于抽样建模(左)情况下，中间层词几乎和其父节点一致，根据前面所说，其表示中间层次的词分配极少，大部分词集中在根节点，这种抽样结果显然不能够很好的解释语料特点。对于随机抽样情况，虽然具有一定的层次树结构，但是各层词明显缺乏主题意义上的聚集。

图8则是经验化建模流程指导下的层次树结构。如根节点展示了这个主题的一个概括性话题主旨，[巴厘]、[大会]、上关于[全球]气体[排放量]的[协议]问题。接下来在第二层的左边第一个节点显示的是各个参与国家[美国]、[联合国]、[欧盟]等关于[温室气体]排放的谈判。第二层左边第二个节点显示关于[同意]、[接受]大会上设定的一些[决议]等。如此分析接下来分别是美国，联合国其他国家关于京都议定书上结果的意见；关于温室气体排放引发的一系列讨论；中国和一些发展中国家以及欧盟对线路图的立场以及时间规划等等。此处由于文档形成的树结构很大，因此我们只选取了几个主要的节点路径上的主要的一些词。同样和人工总结的子主题进行比较发现，其效果是非常好的。

图8 建模结果树状结构图

7 小结

我们针对在实际主题建模过程中的建模效果较差，也大多缺乏具体可依据的建模策略的问题，提出了基于关键因素分析的统一分析建模框架，并在此框架基础上，提出了一个统一的建模流程，实验表明取得了很好的效果。但我们也采用了人工评估的方法进行建模效果的评估，这在一定程度上受个人主观性所限。未来仍然有很多值得努力的方向，如关键因子启发式的自调节，如何自动对建模结果进行合理评估等。

[1] Blei D M, Griffiths T L, Jordan M I, et al. Hierarchical topic models and the nested Chinese restaurant process[M]. Advances in Neural Information Processing Systems 2004,(16): 106-114.

[2] Blei, D M, Griffiths, T L, Jordan, M I. The nested Chinese restaurant process and Bayesian nonparametric inference of topic hierarchies[J]. Journal of the ACM (jACM), 2010,57(2):1-30.

[3] Asli C, Dilek H. A hybrid hierarchical model for multi-document summarization[C]//Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics. 2010(7)： 815-824.

[4] 刘平安. 基于HLDA模型的中文多文档摘要技术研究[D].北京邮电大学硕士论文, 2012.

[5] Geman, Stuart， Donald Geman. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on 1984(6): 721-741.

[6] Smith, Adrian FM, Gareth O. Roberts. Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1993： 3-23.

[7] Blei D M. Probabilistic topic models[J].Communications of the ACM， 2012， 55(4)： 77-84.

[8] Joon H K, Dong W K, Suin K, et al. Modeling topic hierarchies with the recursive Chinese restaurant process[C]//Proceedings of the 21st ACM international conference on information and knowledge management, ACM, New York，2012)(10)： 783-792.

[9] Paisley J, Wang C, Blei D M, et al. Nested Hierarchical Dirichlet Processes[C]//Proceedings of arXiv preprint arXiv, 2012(5).

[10] Rodriguez Abel, Dunson D B. Nonparametric Bayesian models through probit stick-breaking processes[M]. Bayesian Analysis. 2011,6(1)： 145-177.

[11] Ferguson Thomas S. A Bayesian analysis of some nonparametric problems[J]. The annals of statistics, 1973： 209-230.

[12] Bernardo José M, Adrian FM Smith. Bayesian theory[M]. Wiley, 2009.