矿车驾驶室的模态灵敏度分析及其结构优化

张 龙，陈 剑

（合肥工业大学 机械与汽车工程学院；合肥，230009）

车辆 NVH（Noise/Vibration/Harshness）技术是以控制振动、噪声水平来满足用户日益提高的安全保障和舒适乘坐环境的要求。在整车设计阶段，NVH性能成为重要参考指标。

板件等的振动对于NVH性能有至关重要的影响。模态分析作为振动工程理论的一个分支，常被用来确定结构部件等的振动特性，即固有频率和振型。模态分析结果为NVH性能评估和后续开展各种动态结构设计方法提供了强有力的参数依据。

基于CAE仿真技术的结构优化设计整体属于多学科技术综合的优化控制系统，常见种类有形貌优化、尺寸优化等，国内外的学者做过大量理论与实践方面的研究工作［1］。

本课题以某型号矿用自卸汽车驾驶室为研究对象，采用Pro/E建CAD模型，如图1所示。在HyperMesh中完成几何清理、网格划分及相关参数设置前处理。提交文件至MSC.NASTRAN分析求解，获得驾驶室结构动态特性参数。

一阶频率是评价驾驶室动态性能的一个重要指标［2］。

要求驾驶室的各阶固有频率远离外部激励源（如路面不平度，发动机的工作运转，传动系的不平衡等）的频率，避免共振发生。

针对低阶模态频率过低、刚度不足的问题，用OptiStruct求解器作灵敏度分析高效快速选定影响低阶关注模态的灵敏结构部件，将板件的厚度作为设计变量，重新计算模态，结果表明低阶模态频率有了较大程度的提高。

1 有限元建模

有限元分析方法依托计算机技术和数值分析方法的发展，采用“化整为零又积零为整”的数学思想，模型是建立在近似的力学模型上。有限元法进行结构分析的流程如图2所示。

Altair公司开发的Altair HyperWorks软件包是一个创新、开放的企业级CAE平台，集成设计与分析所需的各种工具［3］。其包含的HyperMesh是杰出的有限元分析前后处理平台。

将驾驶室CAD模型导入其中，在保证不影响结构整体动态特性及分析精度前提下做简化处理，删除反光镜及支架、车内饰、橡胶密封件等非承载类零件。

在拓扑模式下针对几何信息转换中存在的边界错位、不必要的缝隙和面的缺失等问题做几何清理，重点修改调整自由边、共享边、压缩边和T形连接边，删除模型中如倒角、圆角、孔等细微特征，抑制小的几何。

驾驶室由钣金冲压薄板零件组合而成，由于壳单元结合了平面应力板单元和受弯曲的薄板单元的共有特征。可以承受平行及垂直板中面的载荷，每个节点有6个自由度，也有6个节点力分量［4］，所以在用Midsurface抽取中面后，选用SHELL单元（QUAD4和不超过总单元10%的TRIA3单元）离散结构，以10尺寸大小划分网格。在网格划分同时需在Quality Index面板中设置单元划分标准，以控制网格的变形。因为这直接关系到有限元分析计算结果的精度和收敛性。实际操作中网格质量检查与网格划分需同步进行。

根据实车结构的连接方式，该驾驶室模型采用Connectors模块提供的一维Rigid单元模拟铆接和螺栓连接的刚度特性及其对周围零件的影响。采用ACM2模型（见图3）模拟点焊，它通过焊核（一个处于两被焊接件间、垂直于被焊接面的六面体单元）和RBE3单元分别与两被焊接件连接而成［5］。

驾驶室板壳材料均为Q345B，属性见表1。

表1 材料属性

玻璃门窗在很大程度上影响结构特性，安装了钢化玻璃的整个驾驶室结构模型有405 323个单元，412 995个节点和1 795个连接体（见图4）。

2 模态分析

2.1 模态分析的理论基础

绝大多数振动的结构在结构动力分析中可将其离散成有限个自由度的多自由度系统，用n个独立的物理坐标描述其物理参数模型。运动微分方程为［6］。

式中：［M］、［C］、［K］分别为系统的质量矩阵、阻尼矩阵和刚度矩阵分别为系统的加速度、速度和位移列向量；［F］为研究对象（系统）所受的激励力。

对系统进行固有模态分析，不考虑阻尼和激励力，即［C］、｛ ｝

F 均为零的情况下，存在：

对于任何线性系统而言，式中的［M］、［K］都是实对称矩阵，求解时设｛x｝=｛φ ｝sin（ωt）代入得

2.2 驾驶室模态结果分析

根据模态频率计算分析规范，释放载荷和约束。由于Block-Lanczos方法采用稀疏矩阵方程求解，运算速度快，输入参数少，特征值、特征向量求解精度高，故文件提交到MSC.NASTRAN中用Lanczos法进行模态计算［8］。

驾驶室结构的前几阶整体模态对振动的贡献度大，同时也反映出驾驶室的整体刚度性能［9］。经MSC.NASTRAN计算得到的固有频率和振型以计算云图显示，例出典型的几阶展示如图5所示。

具体的模态频率和振型描述见表2。

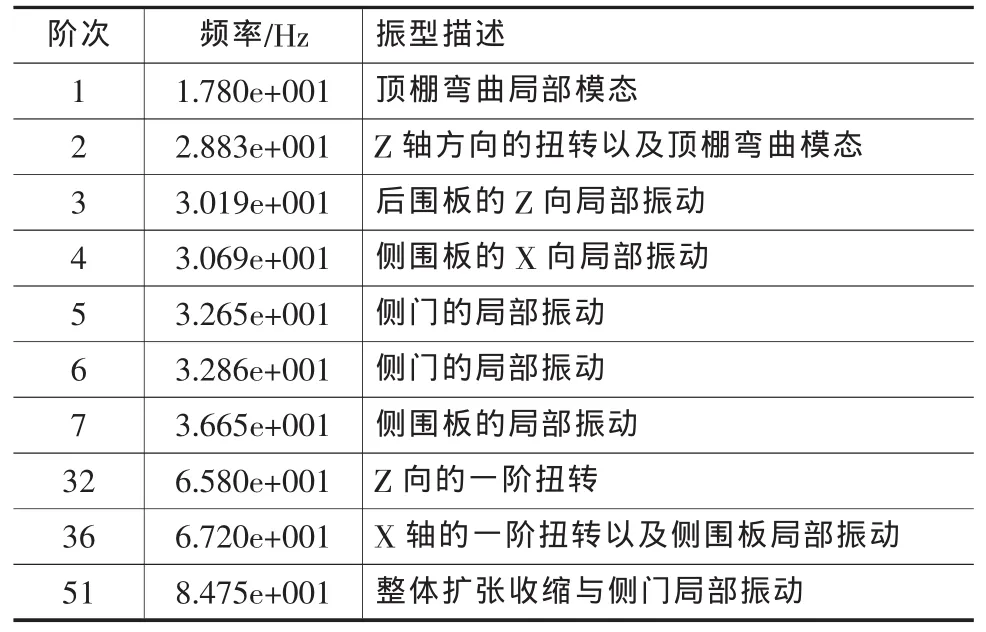
表2 驾驶室整体结构模态频率及其振型

结构的低阶弹性模态不仅反映汽车车身的整体刚度性能，而且是控制汽车常规振动的关键指标。鉴于以往的同类型车辆的研究成果，整体来看，模型建立合理，整体设计满足要求。

该驾驶室存在顶棚、侧围等局部模态过多现象，一阶模态频率偏低，说明其动态刚度偏小。为了在保证驾驶室有必要的结构强度和刚度情况下，可以修改设计方案以提高这些低阶模态频率。

提高低阶模态频率的途径一是应用密度小的材料，如铝、工程塑料等做板件，以降低关注模态的模态质量；另一种是改变驾驶室关键零部件的板厚、材料、泊松比、弹性模量、截面形状和采用加强筋等结构形式与尺寸［10］［11］。

本课题采用的是通过改变板块的尺寸厚度来实现的。

3 驾驶室结构模态特性灵敏度分析

3.1 模态灵敏度分析的理论基础

驾驶室一阶模态灵敏度主要反映驾驶室一阶模态频率对结构设计变量的变化梯度，也就是结构响应对设计变量的偏导数。由模态理论知：

式中：δ为单元节点位移矢量。

根据灵敏度的定义，对设计变量xi求偏倒，得：

将上式左乘δT，由于K为对称矩阵，整理得到：

由式知（Kδ-ω2Mδ）T=0 代入（6）式简化为：

将振型向量对质量矩阵做归一化处理，并对上式简化，结合ω=2πf得到系统的固有频率对设计变量xi的灵敏度关系式：

3.2 板厚对驾驶室一阶频率的灵敏度

选取驾驶室的几个典型部件（见表3）的板块厚度为设计变量，运用Optistruct求解器进行计算分析，以提高一阶模态频率为目标函数，质量上限为原来的99%作为约束条件，即在不增加驾驶室重量的前提下改善振动特性，计算出一阶固有频率对板厚的灵敏度（见图6）。

表3 驾驶室部件

由图6、表3可以看出，顶盖内板、地板内侧、左右门内板等部件板厚的改变对驾驶室一阶模态频率影响较大。

4 优化分析

尺寸优化是Optistruct提供的一种优化设计方法，是在对模型的形状有了一定的设计思路后所进行的一种细节设计［12］，由灵敏度分析确定顶盖内板、地板内侧和左右门内板为修改对象，采用不同厚度进行模态分析，兼顾生产成本，最终确定将顶盖内板和左右门内板厚度提高1.5mm，地板内侧厚度提高3mm，重新计算模态频率如表4所示。

表4 优化后各阶模态频率

5 结论

介绍了驾驶室模型有限元分析的具体流程，用HyperMesh进行几何清理和网格划分，提交MSC.NASTRAN对模型求解、分析模态，进而通过灵敏度分析寻找到灵敏区域，这一分析思路与流程为后续其他的结构修改提供参考，具有一定实际意义。

针对驾驶室一阶模态频率（17.8 Hz）偏低的问题，利用灵敏构件的尺寸优化来指导驾驶室结构的改进与优化设计，进而提高驾驶室的动态特性。结合优化前后的结果对比，可见提出的方案可行，有效的实现了提高一阶模态频率（44.8 Hz）的目标。

［1］刘显贵.基于刚度灵敏度分析的轿车白车身结构优化［J］.机械设计.2009：26（12）：58-60.

［2］曹树谦，张文德，萧龙翔.振动结构模态分析［M］.天津：天津大学出版社.2001.

［3］曾力.基于HyperWorks的卡车车身有限元分析及改进研究［D］.成都：西南交通大学，2010.

［4］ 刘海江，肖丽芳.翼子板结构刚度模态分析与优化 ［J］.机械设计与制造.2009，（1）：4-5.

［5］段月磊，毕传兴.轿车车身刚度有限元分析与优化［J］.噪声与振动控制，2010.（6）：79-82.

［6］刘永超.基于有限元法的微型轿车车身结构的动力学研究［D］.武汉：华中科技大学，2005.

［7］ 杨炯年，钱立军，关长明.某轿车白车身模态分析［J］.机械设计与制造，2010.（2）： 235-237.

［8］ 曹树谦，张文德，萧龙翔.振动结构模态分析［M］.天津：天津大学出版社，2002.

［9］谷正气.汽车车身现代技术［M］.北京：机械工业出版社，2009.

［10］张胜兰.基于HyperMesh的结构优化设计技术 ［M］.北京：机械工业出版社，2008.