基于MASTA的驱动桥主减速器锥齿轮传动分析

刘光军 ，林 科 ，唐善政

（1.上海内燃机研究所 上海 200438；2.上海汽车商用车技术中心，上海200438）

汽车驱动桥主动锥齿轮是汽车传动系统的关键零部件，其工作性能、使用寿命、振动、噪声等在很大程度上取决于齿轮的传动质量［1］。因此，分析驱动桥主减速器锥齿轮传动对提高驱动桥产品的质量有重要的意义。

齿轮接触印迹和传动误差是评定齿轮传动性能好坏的重要依据。由于驱动桥锥齿轮齿面几何拓扑结构非常复杂，加之传统设计方法及制造手段的落后，其啮合质量的控制非常困难［2］。传统方法主要是在滚检机上看配对齿轮的接触区及听传动噪音，这主要依靠有经验的技术人员来保证，过程较为繁琐［3］。利用MASTA对配对齿轮接触印迹和传动误差进行仿真分析将会简便这个调整过程，有利于快速有效地获得良好的齿面接触质量。

1 齿轮接触印迹与传动误差

在齿轮啮合过程中，两齿面连续相切接触，在固定坐标系中，任一时刻两齿面都有公共接触点，且有相同的公法线。由此得到下式成立：

式中：θp、φp、θg、φg分别为小轮和大轮齿面的曲面坐标，φ1、φ2分别为小轮和大轮啮合转角。

式（1）为一个非线性方程组，将方程组中各个矢量分量展开，可得到5个独立的标量方程。而未知数有6个，此时取φ1值为输入值，以一定的步长不断改变，直到接触点超出边界为止。这样给定初值，可以求得其余 5 个参数。 将求得的 θp、φp和 θg、φg分别代入到齿面方程r1→（1）（θp，φp）和r2→（1）（θg，φg）中，即可得到齿面上接触点，这些接触点构成了接触路径。

由图1可得到接触椭圆长轴和短轴方向矢量：

以绘制大轮接触印痕为例，将坐标系Sh下ηh、ζh转换到齿轮坐标系S2中，可得：

在绘制接触印痕时，接触椭圆长轴与短轴与节锥母线的夹角为：

求得每个接触点以后，各接触点接触椭圆的长半轴a和短半轴b可由下式计算得出。

求得一系列接触点处的φ1、φ2，可由下式求得传动误差：

式中：φ1（0），φ2（0）分别为两轮在参考点啮合时的初始转角。

2 MASTA接触印迹与传动误差曲线分析

正确解读齿轮的接触印迹和传动误差曲线，对分析齿轮传动性能、啮合质量以及在实际中的运用都起着至关重要的作用。齿轮的接触迹线和传动误差曲线在实际的过程中是多种多样的，特别是传动误差曲线，所包含的信息量很大，对每一种齿轮可能出现的接触情况，都能在传动误差曲线中反映出来。

2.1 MASTA接触印迹曲线

齿轮接触印迹曲线是齿轮在瞬时接触过程中接触点在齿长和齿高方向的位置，MASTA软件采用局部综合法计算得到的齿轮接触印迹曲线如图2所示。横坐标为齿宽方向，纵坐标为齿高方向，图中的点为齿轮的瞬时接触点，黑线为齿轮的点接触线，红线为潜在的接触椭圆的长半轴的方向及长度。由接触印迹曲线可以得到齿轮接触区域的位置、大小和形状并判断出齿轮是否存在边缘接触。

驱动桥锥齿轮接触区域的位置大概可以分为三种：中间接触，小端接触，大端接触。分别如图3、图4和图5所示。

当齿轮出现小端接触和大端接触时，齿轮传动时将产生严重的振动和噪声，并且大大地缩短了齿轮的使用寿命。正确的齿轮接触印迹曲线应该是齿轮接触斑点位于齿面中间位置，长度为齿全宽的70%左右，高度为全齿高的60%左右，接触区域也不应该太大，否则在受载时容易出现边缘接触，接触区域也不应该太小，这将影响齿轮的传动质量。

2.2 MASTA传动误差曲线

MASTA软件由式（6）计算得到的传动误差曲线如图6所示。齿轮传动误差曲线反映了齿轮啮合的动态特性、载荷分配、重合度和齿面接触特性。

（1）传动误差曲线波动程度可反映出齿轮幅的动态性能，波动幅值愈大，振动愈大，噪音愈大；波动幅值愈小，传动愈平稳。当齿轮传动误差设计幅值较大时，轻载传动误差波动大，而重载时变形补偿作用使波动减小；反之，当设计幅值较小时，轻载传动误差波动小，重载时易出现边缘接触使振动噪音加大。

（2）几何传动误差相邻两条曲线上同一横坐标上的传动误差值反映了可能同时接触的两对齿的初始相对位置。载荷在两对齿间的分配既取决于齿对刚度（变形），也取决于初始间距。

（3）几何传动误差曲线下端宽度与啮合周期之比即为齿轮的设计重合度。重合度越大，轮齿受力越小。理论上重合度大于1齿轮即可连续传动，目前最大能达到3甚至4。当承载传动误差超出几何传动误差下端时，出现边缘接触，即齿面与相啮合齿的齿顶刃接触，产生振动与强度问题。

（4）几何传动误差曲线不交叉（见图7），齿轮出现边缘接触。这在齿轮设计中是应该避免的。

（5）几何传动误差曲线向上弯曲或呈S形（如图7）时，齿面产生桥式接触，伴随严重的振动；各齿对传动误差曲线不连续时（如图7），产生边缘接触。因此，理想的几何传动误差曲线应向下弯曲、齿对间连续且两下端尽量对称，此时产生边缘接触的可能性相对小。

2.3 实例分析

以某驱动桥主减速器锥齿轮为例，齿轮参数如下表所示。根据驱动桥主减速器齿轮、轴和轴承的详细参数在MASTA中建立驱动桥的仿真模型，如图8所示。齿轮基本参数见表1。

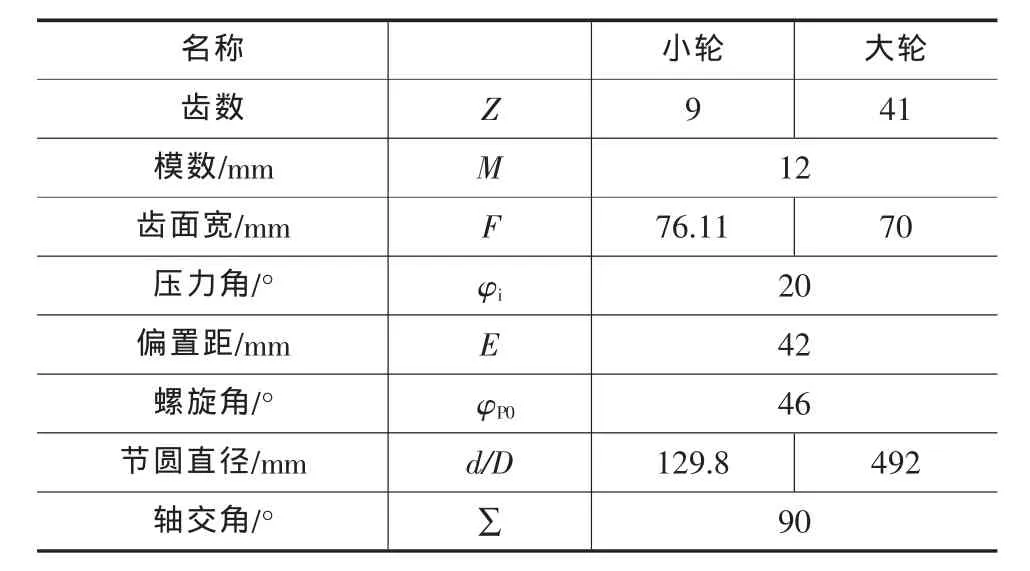
表1 齿轮基本参数

在MASTA中进行驱动桥主减速器齿轮的仿真分析，得到驱动桥主减速器齿轮的接触印迹和传动误差曲线，如图9、图10所示。

由接触印迹曲线可以看出齿轮的接触区域位于齿面中间，大小和形状也比较合适，不产生边缘接触；由于此驱动桥多用于重载工况，故传动误差设计幅值较大。由传动误差曲线计算得齿轮的重合度为3；传动误差曲线交叉，向下弯曲，齿对间连续且基本对称。由此可知，这对齿轮在传动过程中啮合质量较好、振动噪声小、受力均匀，且使用寿命较长。

3 结论

利用MASTA软件仿真计算得到驱动桥主减速器齿轮的啮合印迹和传动误差曲线，全面分析了啮合印迹和传动误差曲线所反映的齿轮传动的众多信息，为锥齿轮啮合质量的评定提供依据，避免了依靠经验的定性评价。并且，在驱动桥主减速器齿轮设计开发阶段，进行齿轮齿面接触的仿真分析，可以有效的减少试验费用，缩短开发周期，为今后的驱动桥主减速器齿轮的开发与运用提供了较好的指导作用。

［1］李永祥，张军顺，陈国定.齿轮TCA技术及发展［J］.机械设计与制造，2009.4：267-268.

［2］方宗德，刘涛，邓效忠.基于传动误差设计的弧齿锥齿轮啮合分析［J］.航空学报， 2002.5（3）：226-230.

［3］罗太景.齿轮传动中的齿面接触斑点分析与质量控制［J］.机械传动 2009.33（3）：114-116.

［4］ Litvin F L，Seol IH，Kim D，et al.Kinematic and Geometric Models of Gear Drives ［J］.Journal of Mechanical Design， 1996.118（12）：544-550.

［5］ Gleason Works.Understanding Tooth Contact Analysis［M］.Gleason Works Publication，1978.