长江口北支河段全潮水文测验水通量平衡计算方法

刘桂平，徐 华，王 珏

(1.长江水利委员会水文局长江口水文水资源勘测局，上海 200136;

2.南京水利科学研究院河流海岸研究所，江苏南京 210029;3.河海大学港口海岸与近海工程学院，江苏南京 210098)

长江口是中等潮汐强度的大型河口，平面呈扇形，为三级分汊、四口入海的河势格局［1］，有北支、北港、北槽、南槽4个入海通道。北支河段位于崇明岛以北，是长江出海的一级汊道，西起上海市崇明岛头，东至江苏省启东寅阳连兴港，全长83 km，区间河道形态多样，沿程涨、落潮量变化大，动力条件复杂。由于涨潮流占优势，长期存在水、沙、盐倒灌南支的现象，北支水、沙、盐倒灌对南支河段的河势及水环境造成明显影响。20世纪80年代以来，为满足河道整治、航道整治、岸线开发利用、水源地建设、滩涂圈围、桥梁建设等工程前期科研、设计、建设的需要，长江口开展了大量全潮水文测验工作，其中北支是重点观测河段之一。实践中发现，北支河段水文测验结果中，时常出现测验区间水通量不平衡现象，给水、沙、盐等物质输移量以及汊道分流比等成果的利用带来困难。笔者对产生这一现象的原因进行分析，并提出北支河段水文测验水通量平衡计算方法。

1 北支河段全潮水文测验中的水通量平衡问题

北支河段青龙港下、三条港断面间距约46.8 km，0 m以下河槽容积约为4.6亿m3，测流断面位置如图1所示。两断面2002年3月8—9日净泄量差值超过2亿m3［2］，也就是说在一个全潮期里，2个断面的水通量差值超过2亿m3，即使考虑区间槽蓄量变化，2个断面水通量的误差值也远远超出了合理范围。类似现象曾多次出现在北支河段以往的水文测验结果中。

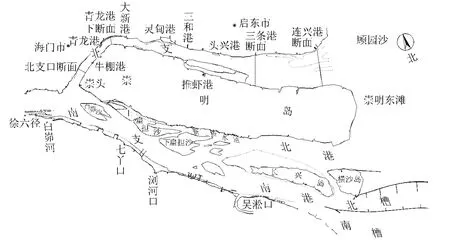
图1 长江口河势及北支测流断面布置Fig.1 River regime of Yangtze River Estuary and layout of observed cross-sections

2 水通量平衡计算主要影响因素

2.1 区间槽蓄量变化对水通量平衡计算的影响

自然状态下，一定区间范围内河流的水量变化应该是平衡的，即在不考虑短期气象和人为活动因素影响的情况下，区间流出水量=区间流入水量+区间槽蓄量增(减)量。受潮汐周期性变化的影响，潮流河段河槽槽蓄量始终处于变化之中，因此，在进行全潮水文测验水通量平衡计算时，应考虑测验区间槽蓄量的变化。

2.2 流量计算误差

在2.1节中，区间流出水量、区间流入水量等于通过水文测验断面的水通量。对于潮流河段，全潮期内水通量等于测验断面涨、落潮量之和，即净泄量。

潮量计算公式为

其中

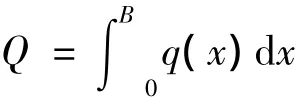
式中:W——潮量;Q——断面流量;t0，t1——相邻的2个憩流时间;B——水面宽;q(x)——单宽流量函数。

天然河道断面形态及流速分布复杂，q(x)难以用数学公式表达，因此一般采用流速面积法求得Q的数值解:

式中:n——部分面积数;qi——相邻两测速垂线间的部分流量。由此可见，潮量误差主要由断面流量计算误差引起。

假定垂线平均流速和水深在2条相邻测速垂线间呈线性分布，将两相邻垂线平均流速和水深的算术平均值作为部分断面的平均流速和平均水深，推导得出实测断面流量计算公式［3］为

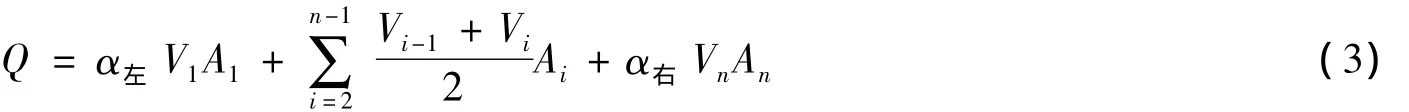
其中

式中:α左，α右—— 左 、右岸岸边流速系数;Vi—— 垂 线平均流速;Ai—— 第i部分面积;Z——测验期间实时潮水位;m——部分面积内微断面数量;Gj，Gj+1——相邻两个测深点的河底高程，采用实测大比例尺断面地形资料;bj——微断面宽，等于相邻两个测深点间距。

推导式(3)时，假定垂线平均流速和水深在2条相邻测速垂线间呈线性分布。实际测量时，测深垂线间距一般为10～15 m，由于距离近，相邻测深垂线间水深按线性分布的假定可以成立。但受测验经费、人员设备、通航安全等条件的限制，测速垂线数量一般较少，测速垂线间距远大于测深垂线间距。对于北支河段，测流断面宽度为2～8 km不等，每个断面布置2～4条测速垂线，测速垂线间距在1～2 km之间。由于测速垂线间距大，且潮流河段水流动力沿断面分布复杂，相邻测速垂线间的流速分布不能按线性变化处理。因此，按照式(3)计算的断面流量存在较大误差，由此引起断面潮量出现较大误差，最终导致测验区间水通量不平衡。

3 水通量平衡下断面流量计算方法

如何提高断面流量计算精度一直是水文部门和水文工作者的研究课题。有关文献［4-5］通过理论论证和实测流量计算验证，对流量计算方法和计算误差进行了分析;杨华等［6］采用有限体积法(FVM)，利用SKM模型对天然河道的水位与流量的关系、断面深度平均流速分布进行了模拟，模拟结果与实测数据吻合良好，认为该方法在河道过流能力、水位等方面的预测合理可行。目前，各种断面流量计算公式都是根据不同的假定提出的。丁文昌公式［7］假定水深在测深垂线间、流速在测速垂线间均为线性分布;钱学伟［8］、贺志岗等［9］、章厚玉等［10］假定各部分宽内单宽流量呈直线变化;谭成志［11］、耿鸿江［12］假定断面河床是均质，水面各点的比降沿河宽横向不变;李惜民等［13］对丁文昌公式进行了改进，但也假定流速在测速垂线间为线性分布。以往对断面流量计算精度的研究大多针对无潮河流且都采用精测法资料进行验证计算，但对如何提高大尺度潮流河段断面流量计算精度研究较少。

按式(3)计算部分断面平均流速时，相邻测速垂线平均流速的权重系数是一样的，均为0.5。在天然河流中，两相邻测速垂线平均流速对部分断面平均流速的贡献是不一样的，故式(3)中流速的权重系数应不相同。为此，将式(3)改为

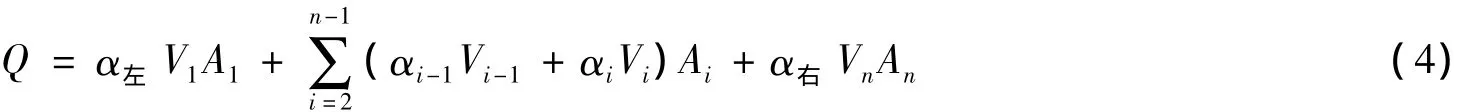
其中

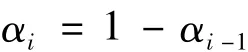
式中αi为第i条测速垂线流速权重系数。由于αi无法直接获得，笔者采用试算法确定其近似值。

3.1 断面流量初算

设A，B，C为某潮流河段3个测流断面，WA，WB，WC分别为各断面全潮期内水通量的近似值，W'A，W'B，W'C为各断面净泄量初算量，wAi，wBi，wCi为各断面测速垂线单宽净泄量。按式(3)计算得到每个断面的潮流量、潮量、净泄量，以及涨潮和落潮起讫时间的初算值。

对于同一断面，流量计算精度主要由测速垂线数量的多少决定。测速垂线越多，精度越高，误差越小;测速垂线越少，精度越低，误差越大。对于不同的断面，在测速垂线布置密度相当的情况下，断面越宽，水流动力分布越复杂，流量计算误差越大。因此，根据各断面净泄量的初算结果，可选择断面宽度小、断面形态简单、测速垂线流速权重系数变动对计算结果影响不大的断面净泄量，代表该断面实际水通量的近似值。

假设经分析计算后，W'A符合作为测验期间A断面水通量近似值条件，则令WA=W'A。以WA作为基准，调整式(4)中流速权重系数，重新计算B断面和C断面的潮流量、潮量及净泄量。

3.2 区间槽蓄量计算

在3.1节中，重新计算B，C断面净泄量之前，需先计算出A～B，B～C之间槽蓄量的变化值。

槽蓄量变化值等于区间上、下游断面潮流闭合起算时刻和结束时刻水面线以下河槽容积的差值，河槽容积可以根据区间河道地形及实测潮水位资料计算得到。

区间槽蓄量计算水位确定方法为:以区间上、下游断面潮流封闭起始时间的平均值作为起算时间，以该时间上、下游断面水位的平均值作为槽蓄量计算的起始水位;按同样方法可得到潮流封闭结束时刻槽蓄量的计算水位，前后2次槽蓄量的差值就是水通量计算时段内区间槽蓄量的变化值。

3.3 测速垂线流速权重系数的调整及断面流量计算

按3.2节所述方法，计算得到断面A～B和断面B～C区间槽蓄量的变化值分别为UAB和UBC，则B，C断面水通量的近似值为

B，C断面全潮净泄量初算值与水通量近似值的误差为

以B断面为例，根据 ΔWB，WB，W'B，wBi之间的数量关系，调试式(4)中各测速垂线流速权重系数 αi，使ΔWB减小至一个合理数值。调试过程如下:

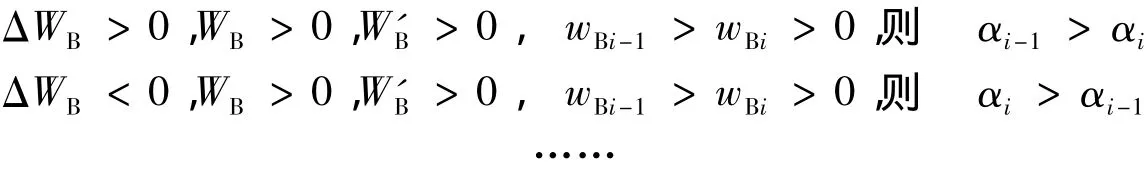
αi和αi-1的数值通过试算确定，所有计算均由计算机完成。

4 实 例 计 算

2010年3月为掌握北支河段水、沙、盐沿程输移及倒灌南支情况，在北支口门、青龙港下游、三条港、连兴港布置4个测流断面，开展大、中、小潮全潮水文测验，测流断面位置如图1所示。北支口门断面采用走航式ADCP测量断面流速、流量，其他断面采用固定测速垂线测量流速、流向，各断面测速垂线布置及断面形态如图2所示。

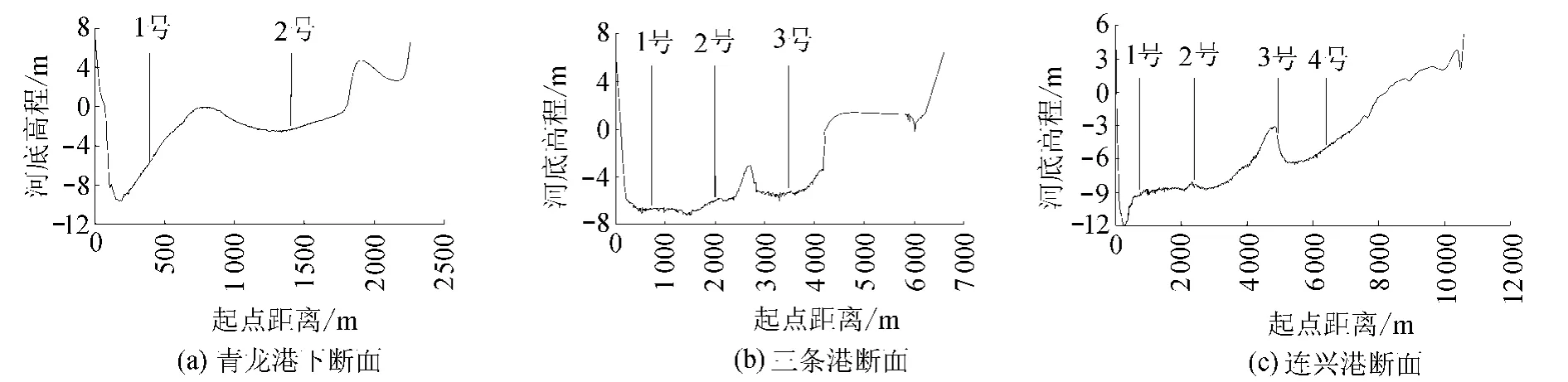
图2 各断面测速垂线布置Fig.2 Layout of cross-sections for velocity measurement

先按照式(4)进行断面流量、潮量及净泄量初算，再按照3.2节中的计算方法计算出区间槽蓄量的变化值，结果见表1。

北支口门断面宽度最小，且采用走航式ADCP施测断面流量，断面流量成果精度可以得到保证，其全潮期内净泄量可以作为该断面测验期间水通量的近似值。北支口门断面潮量及净泄量见表2。

按照式(5)计算得到其他断面水通量近似值，见表3。调试垂线流速权重系数，计算得到青龙港下断面、三条港断面、连兴港断面潮量及净泄量(青龙港下断面大潮期测线移位，未进行断面流量计算)，见表2。

表1 区间槽蓄量变化Table 1 Changes of interval channel storage volume 104 m3

表2 北支各断面全潮潮量统计Table 2 Tidal water volume of cross-sections in north branch 104m3

对照表2和表3可得，各断面全潮净泄量与水通量近似值较为接近，大部分误差约为5%，可将断面净泄量作为水通量的近似值，在考虑区间槽蓄量变化的情况下，各断面之间水通量总体上是平衡的。

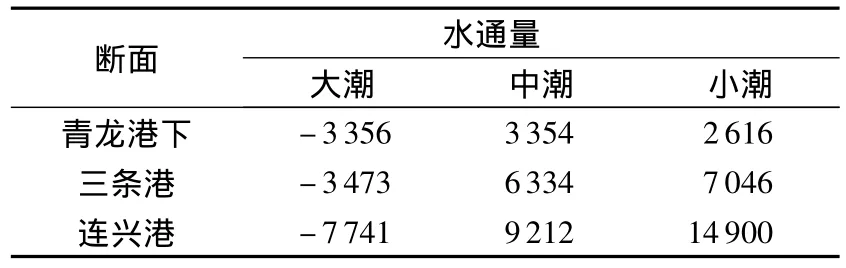
表3 全潮期各断面水通量近似值Table 3 Approximate values of water flux density of cross-sections over entire tide period 104 m3

5 结 语

流量计算是水文测验中的一个重要环节，研究现有水文测验布置条件下大尺度潮流河段流量及水通量平衡计算方法，对于提高全潮水文测验流量计算精度、减少测验投入、提高测验效率非常有益。

笔者根据长江口北支河段水流动力条件、测流断面条件及实际测验布置状况，对现有断面流量计算公式加以改进，在考虑了区间槽蓄量变化对水通量平衡计算的影响情况下，通过试算法确定流速权重系数，依据水量平衡的基本原理进行断面流量和潮量计算，提高了断面流量及潮量的计算精度。此计算方法多次成功运用于长江口河段全潮水文测验流量及水通量平衡计算，解决了以往类似测验中水通量不平衡问题;该计算方法也可在其他类似水文测验中应用。

［1］陈吉余，沈焕庭，恽才兴.长江河口动力过程和地貌演变［M］.上海:上海科学技术出版社，1988.

［2］恽才兴.长江河口近期演变规律［M］.北京:海洋出版社，2004.

［3］GB 50179—1993 河流流量测验规范［S］.

［4］广东水利电力局.流量计算方法的分析［M］.北京:水利电力出版社，1978.

［5］长江流域规划办公室水文局.水文测验误差研究文集(一)［M］.贵阳:贵州人民出版社，1984.

［6］杨华，料华胜，李连侠，等.SKM模型在天然河道的适用性研究［J］.水利水电科技进展，2011，31(3):53-56.(YANG Hua，LIAO Huasheng，LI Lianxia，et al.Applicability of SKM model in natural channels［J］.Advances in Science and Technology of Water Resources，2011，31(3):53-56.(in Chinese))

［7］丁文昌.断面流量计算方法的商榷［J］.水文，1981，1(3):48-50.(DING Wenchang.Discussion on computational method of section discharge［J］.Journal of China Hydrology，1981，1(3):48-50.(in Chinese))

［8］钱学伟.几种实测流量计算方法的比较［J］.水文，1987，7(4):21-26.(QIAN Xuewei.Comparison of some computation formulas the measured discharge.［J］.Journal of China Hydrology，1987，7(4):21-26.(in Chinese))

［9］贺志岗，柳发忠，苏业助，等.断面流量计算方法的探讨［J］.长江工程职业技术学院学报，2006，23(3):22-25.(HE Zhigang，LIU Fazhong，SU Yezhu，et al.Discussion on calculation method of section runoff［J］.Journal of Changjiang Engineering Vocational College，2006，23(3):22-25.(in Chinese))

［10］章厚玉，郎理民，韩念民，等.单宽流量法计算断面流量公式中系数的验证［J］.人民长江，2011，42(13):16-18.(ZHANG Houyu，LANG Limin，HAN Nianmin，et al.Verification of coefficients in calculating formula of cross-sectional discharge using unit width discharge method［J］.Yangtze River，2011，42(13):16-18.(in Chinese))

［11］谭成志.流速-面积法流量计算的讨论［J］.水文，1990，10(1):40-42.(TAN Chengzhi.Discussion on discharge computation of velocity-area method［J］.Journal of China Hydrology，1990，10(1):40-42.(in Chinese))

［12］耿鸿江.实测流量计算方法分析和建议［J］.水文，2007，27(6):61-64.(GENG Hongjiang.Analysis and suggestions of the observed discharge calculation method ［J］.Journal of China Hydrology，2007，27(6):61-64.(in Chinese))

［13］李惜民，高庆森.丁文昌法计算流量的一点改进［J］.水文，2010，30(5):60-63.(LI Ximin，GAO Qingsen.Improvement of Dingwenchang discharge computation method ［J］.Journal of China Hydrology，2010，30(5):60-63.(in Chinese))