不同隙宽条件下L形裂隙水头损失试验

束龙仓，张春艳，闵 星，柯婷婷，唐 然

(河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098)

中国西南地区岩溶分布广泛，面积约54万km2，该地区山地面积大，降水充沛，水资源丰富，但可利用量少，可溶岩成土速率缓慢，土层薄，容许土壤流失量低，水土流失危险度高。因此，开展西南岩溶地区地下水运动规律的研究，对于该地区水土流失以及石漠化的治理、提高该地区水资源利用率具有重要意义［1-3］。

高度非均质岩溶含水介质的水动力参数呈现出显著的尺度效应，仅凭示踪曲线及野外勘察很难识别岩溶系统内部真实的流场分布［4-5］。近年来，越来越多的研究者通过物理模型［6-7］来研究岩溶含水系统的水流运动规律。单裂隙以及十字形交叉裂隙作为裂隙网络的基本构成单元，受到了众多研究者的重视。钱家忠等［8-9］通过大量的试验对单裂隙的水流运动规律进行研究，建立了阻力系数与其影响因素的回归方程以及平均流速与水力坡度之间的指数关系式。王媛等［10］、Quinn等［11］对裂隙水力隙宽的问题进行了探讨。卢占国等［12］对张开度为50-300μm的平行裂隙模型进行了一系列单相流动试验研究，提出可用超立方定律和次立方定律来反映粗糙裂隙的渗流规律。陈雰［13］建立了平行裂隙与管道交叉的室内试验模型，研究了平行裂隙与管道交叉时的渗流水力特性。

综合分析前人的研究成果，大多以平行单裂隙、十字交叉裂隙以及管道与裂隙的交叉模型为研究对象，缺少对L形裂隙中水流水头损失的研究。而在实际的岩溶地区，L形裂隙广泛存在，因此对L形裂隙的研究具有重要意义。笔者以L形裂隙为研究对象，设计试验研究L形裂隙水头损失与隙宽及水流流速的关系。该试验研究主要为笔者基于国家自然科学基金项目所建立的可变隙宽的裂隙网络-管道物理模型的研究奠定基础，试验中L形裂隙的尺寸与裂隙网络-管道物理模型中裂隙单元体的尺寸一致。

1 试验装置、原理及操作

1.1 试验装置

试验装置主要有:有机玻璃制成的4种不同隙宽的L形裂隙，注水筒1个，导水管1根，连接管4根(连接导水管与裂隙，4根接口大小不同的连接管分别连接4种不同隙宽的裂隙)，压力传感器1个(型号为HM20-1-A1-F2-W2，测量范围为 0～100 kPa，精度为 ±0.25%FS)。

隙宽对裂隙水流的运动规律至关重要［14］，试验中由注水体积法测得的隙宽分别为b1=1.354 mm，b2=2.083 mm，b3=2.429 mm，b4=2.967 mm。裂隙的横向宽度c=3 cm，裂隙总长L=L1+L2=20 cm，如图1所示。

图1 L形裂隙示意图Fig.1 Sketch map of L-shaped fracture

1.2 试验原理

试验装置示意图如图2所示。图2(a)与图2(b)中装置连接的唯一区别在于前者中有L形裂隙(虚线框内)，后者无L形裂隙。

图2(a)中，以裂隙出流口中心的水平面为基准面，取水面线所在的断面与L形裂隙出流口过水断面为控制面，对两个控制面列能量方程(连接管管口与裂隙口的大小基本一致，故此连接处的局部水头损失可忽略):

同理，图2(b)中以连接管出流口中心的水平面为基准面，取水面线所在的断面与连接管出流口过水断面为控制面，则可对两个控制面列能量方程:

图2 试验装置示意图Fig.2 Sketch map of experimental device

式中:H1，H2——有、无裂隙条件下的水头差，cm;α——动能校正系数，取 α =1;v1，v2——有、无裂隙条件下出流口水流速度，cm/s;g——重力加速度，取g=980 cm/s2;hf1，h'f1——有、无裂隙条件下注水筒中的沿程水头损失(由于注水筒直径较大，流速较小，故hf1和h'f1可忽略)，cm;hf2，h'f2——有、无裂隙条件下导水管中的沿程水头损失，cm;hj1，h'j1——有、无裂隙条件下导水管与注水筒连接处的局部水头损失，cm;hj2，h'j2——有、无裂隙条件下导水管弯曲处的局部水头损失，cm;hj3，h'j3——有、无裂隙条件下导水管与连接管连接处的局部水头损失，cm;hw——L形裂隙的水头损失，cm。

在某一时刻t1，图2(a)中L形裂隙出流口流量为Q1;在某一时刻t2，图2(b)中连接管出流口流量为Q2。在相同的边界条件下，水头损失的大小只与流速有关，当Q1=Q2时，图2(a)(b)装置对应处的水头损失相等，hf1=h'f1，hf2=h'f2，hj1=h'j1，hj2=h'j2，hj3=h'j3，此时，由式(1)及式(2)得

由式(3)可知，对于某一隙宽的裂隙，只需要知道2次试验过程中的水头差H1和H2，以及出口流速v1和v2，便可得到水流流经L形裂隙时的水头损失hw。

1.3 试验操作

试验操作步骤如下:(a)取隙宽为b1的裂隙，按照图2(a)连接试验装置。(b)注水至注水筒，水流从L形裂隙口流出，打开压力传感器控制系统开始记录数据，直至水面线降至0-0'基准面。(c)除去L形裂隙，此时试验装置如图2(b)，注水至注水筒，水流从连接管管口流出，打开压力传感器控制系统开始记录数据，直至水面线降至0-0'基准面(此时隙宽为b1的裂隙试验结束)。(d)更换连接管(不同隙宽的裂隙，裂隙口大小不一，需用不同的连接管连接)分别取隙宽为b2，b3，b4的L形裂隙，重复步骤2、步骤3。

2 试验数据合理性分析

在有L形裂隙连接的4次试验中，绘制不同隙宽条件下整个试验装置的水头损失hw总(hw总=hf1+hf2+hj1+hj2+hj3+hw)与裂隙出口流速的关系曲线(图3)，从图3可以看出，在出口流速一定的条件下，隙宽越大，试验装置的总水头损失越大，与实际情况相符，表明试验数据是合理的。

在没有L形裂隙连接的4次试验中，试验条件的差别仅在于连接管管口大小不同，故在4次试验条件下，水头差随出口流量(由水头差计算得到水的体积，除以时间即得流量)变化曲线基本一致(图4)。图4表明，4次试验数据较一致，与实际情况相符，说明试验数据较合理。

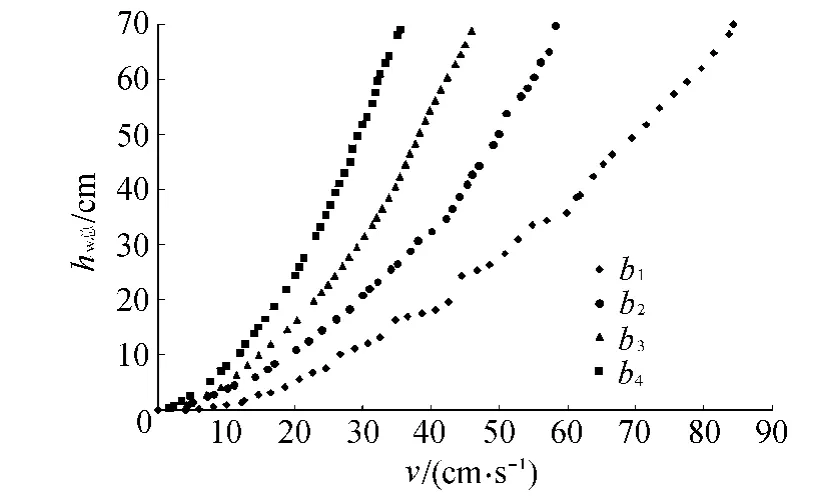
图3 不同隙宽条件下试验装置总水头损失随出口流速变化曲线Fig.3 Total water head loss in experiment vs.flow velocity under conditions of different aperture widths

图4 无裂隙条件下水头差与出口流量关系曲线Fig.4 Water head difference vs.discharge under conditions without fractures

3 L形裂隙水头损失h w的求解

根据试验数据，可以得到有、无裂隙连接条件下水头差与出口流量的关系曲线(图5)。

对图6中的每条曲线确定hw与v的函数关系，可得到不同隙宽条件下L形裂隙的hw与v的关系式:

图5 不同隙宽条件下水头随出口流量变化曲线Fig.5 Water head vs.discharge under conditions of different aperture widths

记hw=Av2+Bv，绘制A和B与隙宽b之间的关系曲线(图7)，得到A和B关于b的关系式:

最终得到L形裂隙水头损失hw关于流速和隙宽的经验公式:

将式(5)代入式(6)并整理得

图6 不同隙宽条件下L形裂隙水头损失随流速变化曲线Fig.6 Water head loss vs.flow velocity for L-shaped fractures with different aperture widths

4 试验结果分析

4.1 试验结果

4次无裂隙试验条件下，水头差与出口流量关系曲线较一致;4次不同隙宽条件下，出口流速一定时，隙宽越大，整个试验装置的水头损失越大。2种试验结果均说明该试验设计较合理，试验数据较准确。

水流流速一定时，L形裂隙的水头损失hw随隙宽b的增大而增大(图6)，这是因为在相同的水头差条件下，隙宽越大，裂隙出口流速越小，由式(3)可知相应的hw越大。hw与v成二次方关系，b越大，二次项系数A越大，且A与b大致呈线性关系。一次项系数B与b呈二次函数关系(图7)，原因可能是裂隙交叉处局部水头损失的影响。

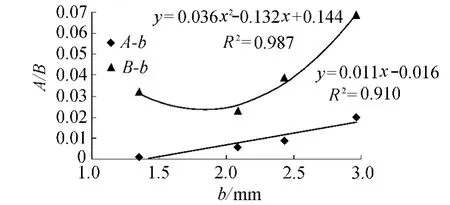
图7 系数A和B关于隙宽b的关系曲线Fig.7 Coefficients A and B vs.aperture width b

4.2 与立方定律比较

1868年俄国著名流体力学家布辛习涅斯基提出了液体在平行裂隙中的运动规律——立方定律:

将q=vb以及代入式(8)得

式中:q——通过裂隙的单宽流量;υ——水的运动黏滞系数;J——水力坡降;v——裂隙中的水流流速;hf——水流流经裂隙的水头损失。

由式(9)可知，水流流经平行裂隙的水头损失与水流流速成线性关系。然而，本次试验的结果是水头损失与流速成二次方关系，原因在于L形裂隙水头损失由裂隙平行部分的水头损失及裂隙交叉处的局部水头损失组成，受局部水头损失的影响，L形裂隙水头损失与流速成二次方关系。

4.3 水头差与隙宽和流速的关系

设连接管半径为r，因为Q1=Q2=Q，则有

由式(3)(7)(10)整理可得

由式(11)可知，水头差与流速呈二次函数关系，与隙宽也呈二次函数关系。

5 结 语

笔者针对不同隙宽条件下L形裂隙水头损失试验所设计的装置构造简单、操作方便，可用于任意形状、任意隙宽的裂隙水头损失试验，具有广泛的适用性。通过试验，方便、准确地得到了不同隙宽条件下L形裂隙的水头损失;相对于流速较小时的试验结果，流速较大时的结果更加准确。综合分析不同隙宽L形裂隙水头损失与流速的关系，得到了水头损失与流速及隙宽关系的经验公式，表明隙宽越大则裂隙水头损失越大，且裂隙水头损失与流速呈二次方函数关系，函数关系式的二次项系数与隙宽呈线性关系，函数关系的一次项系数与隙宽呈二次方关系。本文介绍的只对比较简单的L形裂隙进行的试验研究，所得结论将为下一步研究十字交叉形裂隙、裂隙网络以及粗糙裂隙提供研究基础。

［1］周焱钰，陈喜，张志才.西南喀斯特小流域地下水数值模拟［J］.工程勘察，2011(4):43-51.(ZHOU Yanyu，CHEN Xi，ZHANG Zhicai.Numerical groundwater modeling in a small karst watershed of the Southwest China［J］.Geotechnical Investigation＆ Surveying，2011(4):43-51.(in Chinese))

［2］胡绪江，陈波，胡兴华，等.后寨河喀斯特流域土地资源合理利用模式研究［J］.中国岩溶，2001，20(4):305-309.(HU Xujiang，CHEN Bo，HU Xinghua，et al.Study on the model of rational land use in the karst areas of the Houzhai river basin［J］.Garsologica Sinica，2001，20(4):305-309.(in Chinese))

［3］杨勇.后寨河流域岩溶含水介质结构与地下径流研究［J］.中国岩溶，2001，20(1):17-20.(YANG Yong.A study on the structure of karst aquifer medium and the groundwater flow in Houzhai underground river basin［J］.Garsologica Sinica，2001，20(1):17-20.(in Chinese))

［4］束龙仓，刘丽红，陶玉飞，等.贵州后寨典型岩溶小流域水动力特征分析［J］.河海大学学报:自然科学版，2008，36(4):433-437.(SHU Longcang，LIU Lihong，TAO Yufei，et al.Hydrodynamic characteristic analysis of Houzhai karst watershed in Guizhou Province［J］.Journal of Hohai University:Natural Sciences，2008，36(4):433-437.(in Chinese))

［5］FOURAR M，BORIESS，LENORMAND R，et al.Two-phase flow in smooth and rough fractures，measurement and correlation by porous-medium and pipe flow models［J］.Water Resources Research，1993，29(11):3699-3708.

［6］刘丽红，束龙仓，鲁程鹏.基于管道流模型的岩溶含水系统降雨泉流量响应规律研究:以贵州后寨典型小流域为例［J］.吉林大学学报:地球科学版，2010，40(5):1083-1089.(LIU Lihong，SHU Longcang，LU Chengpeng.Precipitation and discharge response mechanism based on conduit flow model in karstic water system:application the Houzhai karstic water system of Guizhou Province［J］.Journal of Jilin University:Earth Science Edition，2010，40(5):1083-1089.(in Chinese))

［7］季叶飞，束龙仓，董贵明，等.基于物理试验的岩溶区PSSK转化关系研究［J］.水文地质工程地质，2010，37(2):91-94.(JI Yefei，SHU Longcang，DONG Guiming，et al.A study of the transformation mechanism of a precipitation-soil water-surface water-karst water system based on physical experiments［J］.Hydrogeology ＆ Engineering Geology，2010，37(2):91-94.(in Chinese))

［8］钱家忠，刘咏，赵卫东，等.单一流径基岩水流阻力系数的试验研究［J］.焦作工学院学报，1998，17(3):183-186.(QIAN Jiazhong，LIU Yong，ZHAO Weidong，et al.Testing study of the resisitance coefficient of the fissure flow in single fissure［J］.Journal of Jiaozuo Institute of Technology，1998，17(3):183-186.(in Chinese))

［9］QIAN Jiazhong，ZHAN Hongbin，ZHAOWeidong，et al.Experimental study of turbulent unconfined groundwater flow in a single fracture［J］.Journal of Hydrology，2005，311:134-142.

［10］王媛，速宝玉.单裂隙面渗流特性及等效水力隙宽［J］.水科学进展，2002，13(1):61-68.(WANG Yuan，SU Baoyu.Research on the behavior of fluid flow in a single fracture and its equivalent hydraulic aperture［J］.Advances in Water Science，2002，13(1):61-68.(in Chinese))

［11］QUINN P M，PARKER B L，CHERRY J A.Using constant head step tests to determine hydraulic apertures in fractured rock［J］.Journal of Contaminant Hydrology，2011，17:85-99.

［12］卢占国，姚军，王殿生，等.平行裂缝中立方定律修正及临界速度计算［J］.实验室研究与探索，2010，29(4):14-16.(LU Zhanguo，YAO Jun，WANGDiansheng，et al.Correction of cubic law and calculation of critical velocity in parallel fractures［J］.Research and Exploration in Laboratory，2010，29(4):14-16.(in Chinese))

［13］陈雰.岩溶与裂隙交叉渗流特性试验及数值模拟研究［D］.南京:河海大学，2006.

［14］速宝玉，詹美礼，赵坚.光滑裂隙水流模型实验及其机理初探［J］.水利学报，1994，25(5):19-24.(SU Baoyu，ZHAN Meili，ZHAO Jian.The model test of the folw in smooth fracture and the study of its mecchanism［J］.Journal of Hydraulic Engineering，1994，25(5):19-24.(in Chinese))