胶凝堆石料大三轴试验

蔡 新，宋小波，明 宇，杨 杰

(1.河海大学力学与材料学院，江苏南京 210098;2.河海大学水利水电学院，江苏南京 210098)

胶凝堆石坝是以坝址附近河床砂砾料及开挖弃渣为骨料，加入水泥等添加剂简易拌和成坝料进行填筑的，众多学者都认为该坝型具有高安全性、高抗震性和对地基条件要求低的特点，而且施工简便、快速，造价低廉。而胶凝材料的力学特性试验及其本构模型研究是胶凝堆石坝相关问题的关键，目前国内对胶凝堆石料本构模型的研究还不够深入，本文结合大三轴试验，对不同胶凝体质量浓度的本构模型进行探讨。

胶凝堆石料的变形模量是碾压堆石料的10～100倍，使相应坝型的坝体变形大幅度减小，有利于改善面板和周边缝的工作性态，上游防渗体系能正常工作。但目前对胶凝堆石料的本构特性认识还不够深入，多是将胶凝堆石料看作混凝土材料，采用线弹性本构关系来模拟;也有将其按照堆石料进行处理，采用邓肯-张本构关系或将其进行修正来使用［1-2］。笔者对不同胶凝体质量浓度的堆石料进行大三轴试验，通过试验数据对胶凝堆石料的本构特性进行探讨。

1 试 验 过 程

1.1 材料配比

根据前人的试验经验［3-6］，最优水灰比(质量分数)定为0.6～1.2，最优砂率取20%，碎石级配取5～10 mm，10～20 mm，20～40 mm，相应的质量分数分别为20%，35%，45%。试验材料用量见表1。

表1 Ø300 mm×700 mm试件配料Table 1 Ingredients of specimens ofØ300 mm×700 mm

1.2 试件制备

按照《水工混凝土试验规范》对某胶凝材料的配料进行拌和，并用振动碾将拌合物振实。试件成型后，在材料初凝前1～2h需要进行抹面，要求沿模口磨平。模量与阻尼比试验试件要在4种围压、1种固结比下进行试验，也就是每种胶凝体质量浓度的试件要制作4个。考虑到试验失败等不良因素的影响，备用试件为6个。3种试件总计18个，备用试件共20个。在试验前将准备好的止水橡胶模套在试件上。

1.3 试验方法

试件养护28 d后进行分组，每组试验4个试件，分别在恒定围压300 kPa，600 kPa，900 kPa，1200 kPa下饱和固结(固结比K均为1)，固结完成后以0.02 mm/s的加荷速度进行三轴排水(CD)剪切，并记录轴向压力、轴向位移和排水量。当轴向应变值达到15%或试样完全破坏时停止试验。

2 试验数据分析

不同胶凝体质量浓度、不同围压下的胶凝堆石料应力-应变关系曲线即σ1-σ3～εa曲线见图1(σ1为轴向应力，σ3为围压，σ1-σ3为偏应力，εa为轴向应变)。

2.1 胶凝材料试验结果分析

a.由图1(a)可知:当胶凝体质量浓度为20 kg/m3时，曲线没有明显的应力峰值和应变软化现象，试样应力-应变关系曲线近似于双曲线。

b.由图1(b)(c)(d)可知:(a)当胶凝体质量浓度大于20 kg/m3时，胶凝堆石料试样具有明显的应力峰值，σ1-σ3达到峰值前随εa的增加而增长，存在明显的线性初始段，而且围压对该直线段斜率的影响不明显，表现出类似混凝土的应力-应变特征;但随着εa的增长，梯度逐渐变缓，表现出非线性的应力-应变特征。(b)σ1-σ3达到峰值后，εa继续增大，而σ1-σ3逐渐减小，表现出应变软化的特征。(c)随着εa的继续增大，σ1-σ3逐步趋于一个定值，即材料的残余强度。(d)峰值强度和残余强度随着围压的增大而增长。

c.胶凝体质量浓度大于20 kg/m3时，曲线的峰值强度和初始模量随着胶凝体质量浓度的增长而增长，峰值强度对应的εa比较小。

d.胶凝体质量浓度越大，应变软化现象越明显。与纯堆石料相比，胶凝堆石料的强度和初始变形模量都有大幅度提高。

2.2 邓肯-张本构模型的适用性

当胶凝体质量浓度为20 kg/m3时，试样的应力-应变关系曲线近似于双曲线。采用修正邓肯-张本构模型进行验证，其表达式［7-8］如下:

式中:Et——切线弹性模量;Ei——初始弹性模量;φ——内摩擦角;c——黏聚力;Rf——模型参数。

由于胶凝堆石料有一定的抗拉能力，故对原有的表达式进行修正［9］:

图1 三轴试验应力-应变曲线Fig.1 Stress-strain curves for specimens in triaxial tests

得到修正模型的表达式如下:

切线弹性模量

切线体积模量

式中:K，n——模型参数;pa——大气压强;σt——胶凝堆石料的抗拉强度;Kb，m——模型参数。

利用试验数据拟合［10-11］，最终得到参数c=174.4kPa，φ = 40.6。，K=1196.74，n=0.207，Rf=0.79，Kb=407.72，m=0.36。当胶凝体质量浓度大于20 kg/m3时，应力-应变曲线和拟合的试验数据表明邓肯-张本构模型已经不再适用，对其本构模型还要进行深入的探讨。

3 本构模型探讨

从应力-应变关系曲线中可以看到:当胶凝体质量浓度大于20 kg/m3时曲线在初始弹性阶段表现出明显的线性特征;随着轴向应变的增长，梯度逐渐变缓，表现出非线性的应力-应变特征。然而通过图1可以看到曲线在应变软化之前非线性部分基本接近于曲线峰值点，此时应已脱离弹性阶段而达到了屈服阶段。因此，在弹性阶段内认为应力-应变关系可以用线弹性模型来描述［12］。

3.1 弹性模量的计算

从应力-应变关系曲线中可以发现弹性模量的大小与胶凝体质量浓度、围压有关，为此可以列出表达式:

式中:Ej——弹性模量;f(σ3，H)——弹性模量随围压与胶凝体质量浓度增长的函数;H——胶凝体质量浓度。

要得出弹性模量的表达式，先要通过试验得出材料在不同胶凝体质量浓度和围压下的Ei。所得结果见图2。

对图2曲线进行拟合，发现用指数函数拟合效果较好，拟合结果见表2。可以看出，拟合方程的一般式为y=aekx，k值变化不大(在0.001 6左右)，参数a随围压的增大而增大，二者基本呈线性关系。拟合的σ3～a的关系线见图3，拟合方程为y=49.74x+94.23。

图2 初始弹性模量与胶凝体质量浓度关系曲线Fig.2 Relationship between initial elastic modulus and CSG content

表2 拟合方程Table 2 Fitting equations

综上，可以得到

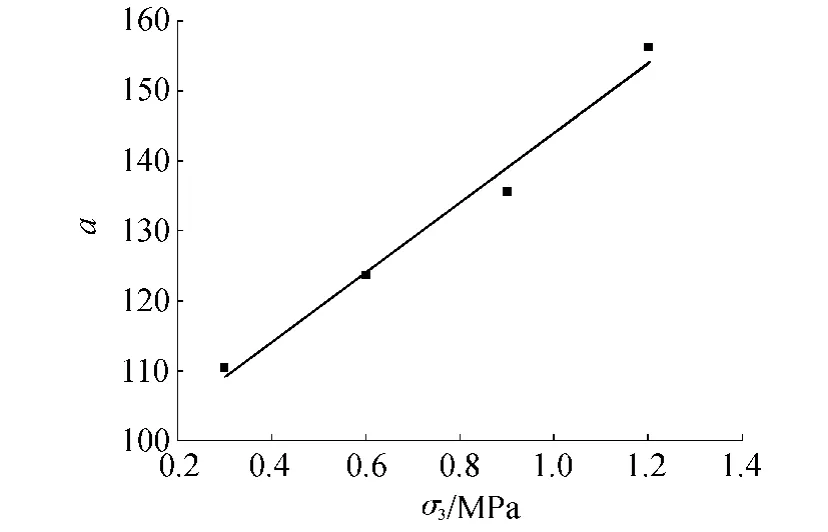
图3 σ3～ a曲线Fig.3 σ3-a curve

4 结 语

a.通过试验数据总结得出结论:胶凝堆石料在胶凝体质量浓度较低时符合邓肯-张本构模型。在此基础上推导出切线弹性模量Et与切线体积模量Bt表达式中的参数值。

b.随着胶凝体质量浓度的增加，由应力-应变曲线可以看出邓肯-张本构模型已不再适用，但曲线初始段表现出明显的线性特征，非线性部分基本都接近于曲线峰值点。因此，认为在弹性阶段内应力-应变关系可以用线弹性模型来描述，它是围压σ3与胶凝体质量浓度H的函数。通过试验数据拟合得出了该函数的表达式。

c.目前工程界对于胶凝堆石料的拌和方式还没有较一致的认识，文中介绍的试验是在室内较理想条件下进行的，试验采用的胶凝材料掺量、最大料径、拌和方式和抽样方法与工程实际有较大出入，得出的结果距工程实际应用有差距，今后还有大量的工作要做。

［1］蔡新，武颖利，李洪煊，等.胶凝堆石料本构模型研究［J］.岩土工程学报，2010，32(9):1340-1344.(CAI Xin，WU Yingli，LI Hongxuan，et al.Constitutive equation for CSG materials［J］.Chinese Journal of Geotechnical Engineering，2010，32(9):1340-1344.(in Chinese))

［2］孙明权，杨世峰，张镜剑，等.超贫胶结材料本构模型［J］.水利水电科技进展，2007，27(3):35-37.(SUN Mingquan，YANG Shifeng，ZHANG jingjian，et al.Study on constitutive model for over lean cemented material［J］.Advances in Science and Technology of Water Resources，2007，27(3):35-37.(in Chinese))

［3］李永乐，侯进凯，孙明权，等.超贫胶结混凝土的力学特性试验研究［J］.人民黄河，2007，29(3):59-60.(LI Yongle，HOU Jinkai，SUN Mingquan，et al.Test and study on mechanical property of super-short cement concrete［J］.Yellow River，2007，29(3):59-60.(in Chinese))

［4］孙明权，彭成山，李永乐，等.超贫胶结材料三轴试验［J］.水利水电科技进展，2007，27(4):46-49.(SUN Mingquan，PENG Chengshan，LI Yongle，et al.Triaxial test of over lean cemented material［J］.Advances in Science and Technology of Water Resources，2007，27(4):46-49.(in Chinese))

［5］彭成山，张学菊，孙明权.超贫胶结材料特性研究［J］.华北水利水电学院学报，2007，28(2):26-29.(PENG Chengshan，ZHANG Xueju，SUN Mingquan.Research of super poor cemented material characteristic［J］.Journal of North China Institute of Water Conservancy and Hydroelectric Power，2007，28(2):26-29.(in Chinese))

［6］唐新军，陆述远.胶结堆石料的力学性能初探［J］.武汉水利电力大学学报，1997，30(6):15-18.(TANG Xinjun，LU Shuyuan.Preliminary research on mechanical behaviors of cemented rockfill material［J］.Engineering Journal of Wuhan University，1997，30(6):15-18.(in Chinese))

［7］朱俊高，周建方.邓肯E-ν模型与E-B模型的比较［J］.水利水电科技进展，2008，28(1):4-7.(ZHU Jungao，ZHOU Jianfang.Comparison of DuncanE-νandE-Bmodels［J］.Advances in Science and Technology of Water Resources，2008，28(1):4-7.(in Chinese))

［8］钱家欢，殷宗泽.土工原理与计算［M］.北京:中国水利水电出版社，1996:220-265.

［9］宿辉，党承华.邓肯-张非线性模型研究及其在ANSYS中的实现［J］.中国农村水利水电，2010(3):76-79.(SU Hui，DANG Chenghua.Duncan-Chang nonlinear elastic model and realization in ANSYS［J］.China Rural Water And Hydropower，2010(3):76-79.(in Chinese))

［10］吴文峰，来妙法.堆石材料邓肯模型参数统计规律研究［J］.浙江水利水电专科学校学报，2008，20(2):5-8.(WU Wenfeng，LAI Miaofa.Statistical research on parameters of Duncan model of rock-fill materials［J］.Journal of Zhejiang Water Conservancy and Hydrapower College，2008，20(2):5-8.(in Chinese))

［11］张波，汪传斌，黄德强，等.邓肯模型参数k，n，Rf整理方法研究［J］.西部探矿工程，2012(7):156-159.(ZHANG Bo，WANG Chuanbin，HUANG Deqiang，et al.Method research for Duncan model parameters ofk，n，Rf［J］.West-China Exploration Engineering，2012(7):156-159.(in Chinese))

［12］吴梦喜，杜文武，姚元成，等.筑坝硬填料三轴试验及本构模型研究［J］.岩土力学，2011，32(8):2241-2250.(WU Mengxi，DU Wenwu，YAO Yuancheng，et al.Triaxial tests and a new constitutive model of hardfill material［J］.RocKand Soil Mechanics，2011，32(8):2241-2250.(in Chinese))