下游折坡点位置对重力坝抗震性能的影响

曹学兴，何蕴龙，冯 蕊，熊 堃

(1.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072;2.华能澜沧江水电有限公司，云南 昆明 650214;3.长江勘测规划设计研究院，湖北 武汉 430010;4.国家大坝安全工程技术研究中心，湖北 武汉 430010)

重力坝具有坝身溢流、形式简单、对地基要求低、抗震性能好［1-3］等优点，因此在国内外大坝建设中得到广泛采用。迄今为止，除了1999年台湾“9·21”大地震中石冈重力坝由于活断层穿过坝体而导致3个坝段破坏外，没有一座重力坝因地震而溃坝［4］。重力坝在地震中表现出了很好的抗震性能:Lower Crystal Springs拱型重力坝在1906年旧金山大地震(M=8.3)时离断层只有400 m，但未发生任何震害［5］;宝珠寺重力坝在设计中并未考虑地震作用，但却经受住了2008年汶川地震的考验(坝址烈度为8度)［6-7］。但一些重力坝震害工程表明，地震过程中大坝坝颈结构突变处容易出现裂缝，是抗震薄弱部位。印度的柯依那重力坝在1967年的地震中大坝折坡处出现大量水平裂缝;遭受过8度以上强震的中国新丰江大坝［8］和伊朗的Sefid Rud［9-10］大坝，在近坝顶结构转折处都发生水平向延伸的上下游贯穿裂缝。研究发现下游折坡点的位置过低对大坝抗震性能尤其是坝颈部位的抗震安全性有较大的影响。笔者从震害工程和有限元计算两方面说明下游折坡点位置过低对重力坝抗震性能的不利影响，通过敏感性分析给出重力坝合理的下游折坡点位置，并通过对云南某工程线性和非线性动力有限元时程分析，进一步验证下游折坡点位置过低时大坝抗震性能较差。

1 下游折坡点位置过低对重力坝抗震性能的不利影响

1.1 震害工程

柯依那重力坝位于印度孟买市东南部的戈伊纳河上，最大坝高为103 m，全长853 m。图1(a)给出了柯依那大坝非溢流坝典型断面，其中下游折坡点距坝顶距离h=36.6 m，为坝高H的35.5%。大坝在1967年12月11日遭受到6.5级地震的作用，震中在大坝以南偏东2.4 km［11］，震中烈度为8度。地震作用后，大坝在13～18号坝段及25～30号坝段的下游面折坡附近处出现水平裂缝，在10～18号坝段及24～30号坝段的上游面相应于下游面折坡处以下6～7 m的范围出现裂缝，裂缝分布如图1(b)所示。

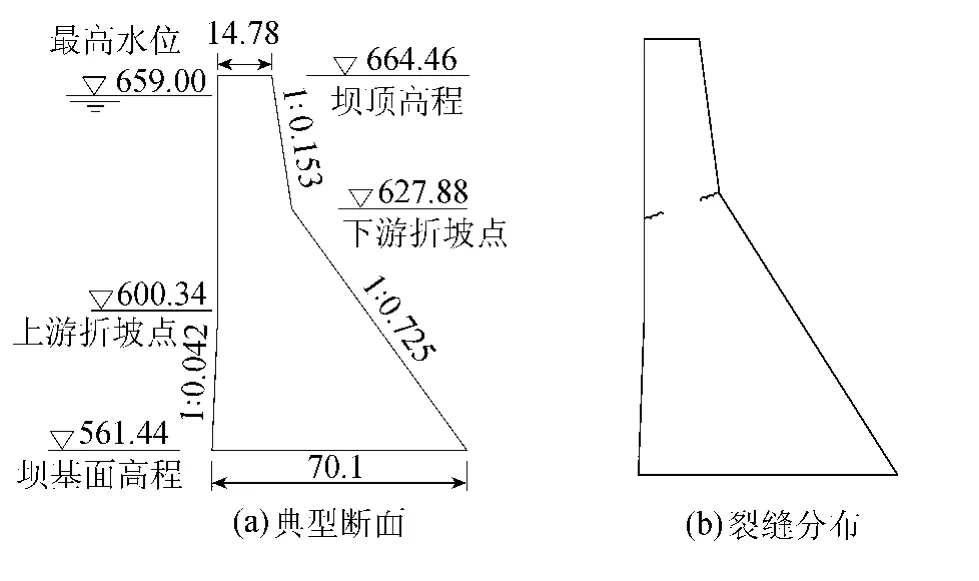
图1 柯依那大坝非溢流坝段断面及震害示意图(单位:m)Fig.1 Sketch map of retaining section of Koyna Dam and earthquake damage(units:m)

1.2 有限元计算分析

1.2.1 计算方案

选取h分别为10m，20m和30 m的高为103m的3个典型重力坝(图2)作为3个基本方案，分析下游折坡点位置对坝体地震动应力的影响。3个方案的坝体顶宽、底宽相同，折坡点以上坝坡为直坡。采用反应谱法对大坝空库情况下的地震动力响应进行分析，坝体动弹性模量为33.15 GPa，泊松比为0.167，密度为2400 kg/m3;坝基上下游和深度方向均取2.5倍坝高范围，坝基岩体弹性模量为20.00 GPa，泊松比为0.200，采用无质量地基。采用DL5073—2000《水工建筑物抗震设计规范》中的标准反应谱曲线进行计算，特征周期为0.2 s，加速度峰值取0.3g。

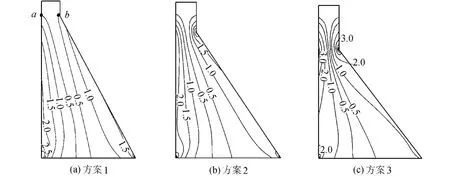
图2 竖直向最大动拉应力分布(单位:MPa)Fig.2 Maximum dynamic tensile stress in vertical direction(units:MPa)

1.2.2 下游折坡点位置对重力坝动应力影响规律

在坝体上取点a和点b(图2(a))对坝颈部的动应力情况进行分析，其中点a位于下游折坡点相应的上游面，为避免应力集中影响，点b位于坝内距下游折坡点1 m位置处。重力坝的动应力计算结果见表1，3个方案坝体在地震荷载作用下竖直向最大拉应力分布见图2。

由表1和图2可知，在地震作用下，当下游折坡点位置较高时，在坝颈结构转折处不会出现应力集中;随着下游折坡点位置的降低，坝体上、下游折坡处动应力明显增大，当下游折坡点位置过低时上、下游折坡处产生明显的应力集中。方案2下游折坡处与上游面相应位置的动应力分别为方案1的3.76倍和4.00倍。方案3下游折坡处应力集中现象非常明显，同时上游面相应位置也有较大动应力;下游折坡处与上游面相应位置的动应力值分别为方案1的7.17倍和7.64倍，动应力值远远超过了混凝土动态抗拉强度，而这个部位坝体又比较薄弱，在地震作用下很容易发生开裂乃至上下游裂缝贯通破坏。

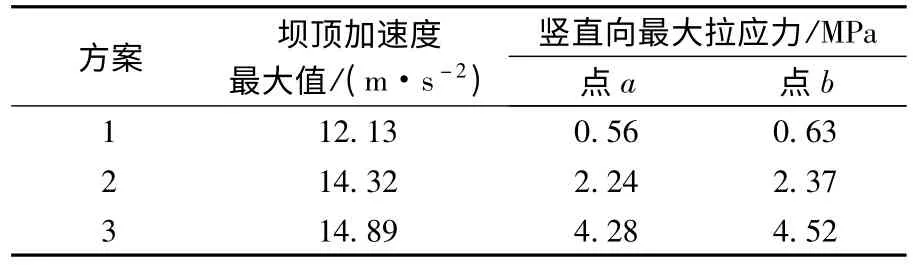
表1 重力坝动应力计算结果Table 1 Results of dynamic stress calculation for gravity dam

1.3 合理的下游折坡点位置

为进一步分析下游折坡点位置对坝颈部位动应力的影响，并确定下游折坡点的合理位置，在3个基本方案的基础上，计算了h分别为12m，14m，16m，18m，22m，24m，26m，28m的坝体整体动应力和坝颈部特征点的动应力，同时对高为50 m和120 m的典型重力坝动应力也进行了相应计算，以说明不同坝高对下游折坡点位置的影响。

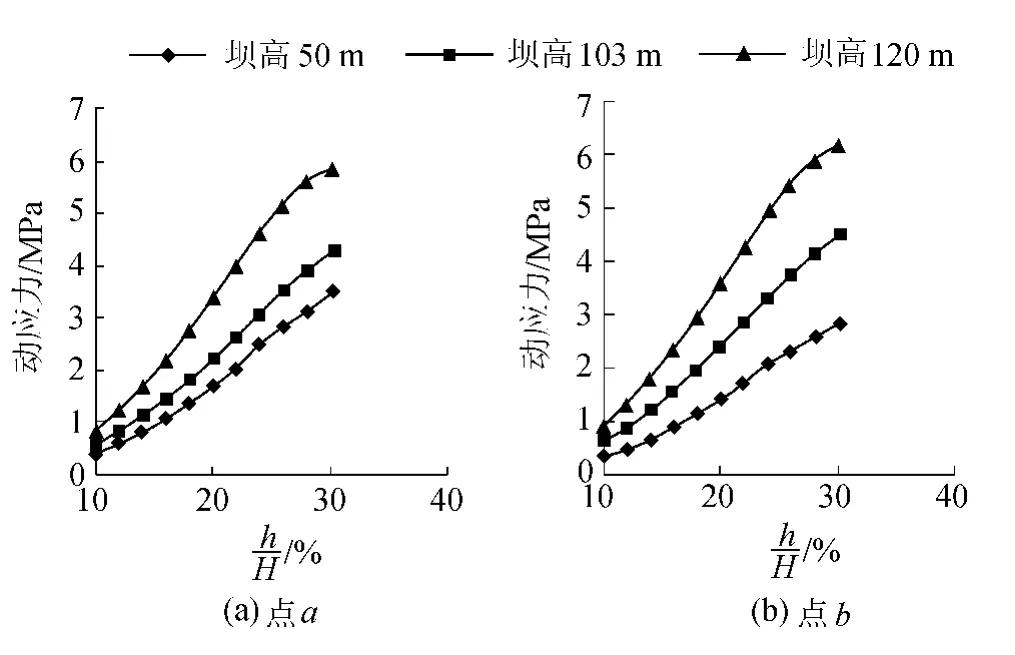
图3 动应力值随折坡点位置变化曲线Fig.3 Relationship between dynamic stress and position of downstream turning point

图3为动应力与下游折坡点位置的变化曲线。从图3可以看出，相同坝高时，2个特征点的动应力随下游折坡点位置的降低而增大;下游折坡点位置相同时，2个特征点的动应力随坝高的增加而增大;对于50 m高重力坝，当下游折坡点位置低于坝高的20%时，特征点的动应力达到了1.5 MPa以上，而120 m高的重力坝达到3 MPa以上;100 m高重力坝下游折坡点位置低于坝高16%时动应力超过1.5 MPa。因此，在工程设计中可以考虑提高坝颈部位混凝土标号，利用圆弧代替直线转折结构;在8度及以上地震烈度区，高度小于100 m的重力坝折坡点位置不宜低于坝高的20%;坝高超过100 m时，除需要进一步提高折坡点位置外，必要时还需采取配置抗震钢筋、坝底铺设铅加球墨铸铁［12］等措施。

2 工程实例分析

2.1 工程概况

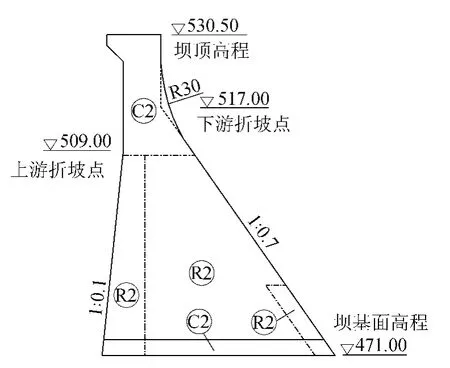
图4 大坝非溢流坝段断面位置Fig.4 Sketch map of retaining section of dam

云南某水电站水库总库容为2 537×104m3，电站装机容量为58 MW，碾压混凝土重力坝最大坝高为65.50 m，坝顶长为357 m。大坝典型非溢流坝段最大坝高为59.5 m，下游折坡点距坝顶13.5 m，折坡点低于坝高的20%(图4)。根据《中国地震动参数区划图》［13］，该工程河流流域内50年超越概率10%的地震动峰值加速度为0.3g。

2.2 混凝土非线性开裂本构模型

计算采用的混凝土非线性应力应变关系曲线如图5所示，其中σc为抗压强度，ec为σc对应的压应变，σu为残余强度，eu为极限压应变，em为极限拉应变，σt为抗拉强度，et为σt对应的拉应变。当e＞0时，材料受拉，在达到抗拉强度σt之前，应力应变关系为线性，此时采用初始弹性模量E0计算应力;当e＜0时，材料受压，按图5所示曲线计算应力。图中曲线为单调加载的应力应变关系，卸载以及再加载时则都使用E0。

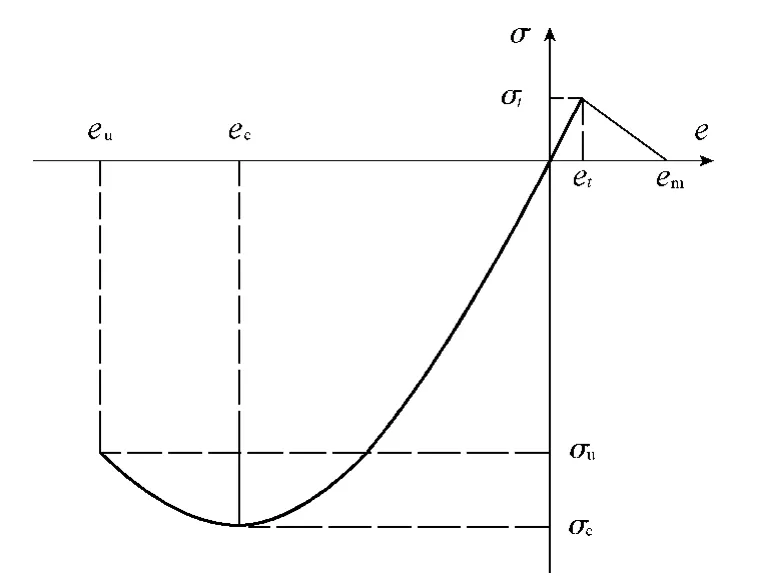
图5 混凝土非线性应力应变关系Fig.5 Nonlinear relationship between stress and strain of concrete

当材料压应力超过σc时发生受压破坏，此时各方向应变均发生软化，直至达到eu，对于超出eu的状态，压应力按照软化弹性模量线性降到零。采用弥散型裂缝模型模拟材料的开裂特性，当拉应力超过σt时，材料进入受拉破坏阶段。此时假设一个破坏面在垂直于相应主应力的方向发展，材料破坏后的性质表现为通过破坏面的法向和切向刚度与拉应力降低，并且假设受拉破坏面处于平面应力状态。计算刚度矩阵所用的新材料弹性矩阵为

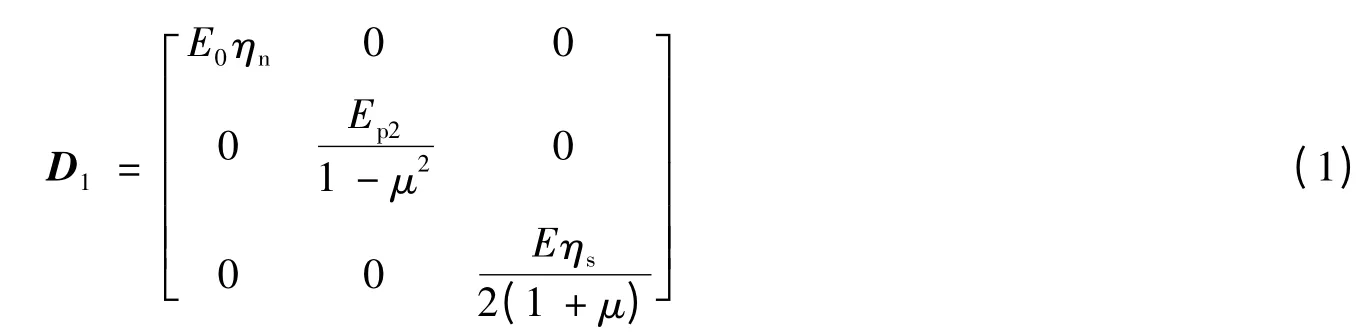
式中:ηn，ηs——法向和切向刚度折减系数，取ηn=0.0001以避免出现奇异矩阵，ηs则处于0和1之间，体现材料开裂后骨料的剪切咬合效应;Ep2——根据第2个积分点应力计算的弹性模量;μ——泊松比。

对于受拉破坏面法线方向的拉应力和破坏面平面内的剪应力，使用总应变计算总应力，其弹性矩阵为

式中:Ef——破坏面法向弹性模量;Gf12，Gf13——切向弹性模量。

此时，Ef与Gf按照线性软化的应力应变关系计算(图6)，图中ηf，σt，et分别为切向弹性模量折减系数、t时刻的拉应力、t时刻的拉应变。由图6(a)可知，当拉应力超过σt时材料出现微裂纹，但破坏面法向仍可承担一定的拉应力;当拉应变逐渐增长达到极限拉应变时，材料破坏面法向拉应力为零，产生宏观裂缝。由图6(b)可知，随着拉应变的增大，剪切弹性模量逐渐降低，最终下降到ηs所对应的弹性模量值。

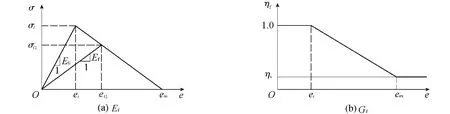
图6 混凝土开裂后的本构关系Fig.6 Constitutive relation of concrete after cracking

为获得一个不受网格约束的解，加入材料断裂能Gf，基于单元尺寸在每个积分点计算极限拉应变:

式中hc为单元特征尺寸，取为单元积分点所控制面积的平方根值。

2.3 有限元计算模型

图7给出了大坝-坝基二维有限元模型，在有限元网格划分过程中，模拟了重力坝主要材料分区与坝基的地质情况。坝基上、下游和深度方向均取2倍坝高。有限元网格以4节点四面体单元为主，因为网格过渡含有部分三角形单元，因此整个模型共有节点3694个、单元3512个。坝体混凝土材料力学参数见表2。弱风化岩体弹性模量取5.5 GPa，泊松比为0.26;微风化岩体弹性模量取6.5 GPa，泊松比为0.25;动弹性模量在静弹性模量的基础上提高30%，采用无质量地基方案。根据DL 5073—2000《水工建筑物抗震设计规范》反应谱生成人工地震波，特征周期取0.2 s，反应谱代表值取2.0，设计加速度代表值为0.3g。输入地震波历时30 s，竖直向设计地震波加速度的代表值取水平向设计加速度代表值的2/3，顺河向和竖直向地震波加速度时程曲线如图8所示。

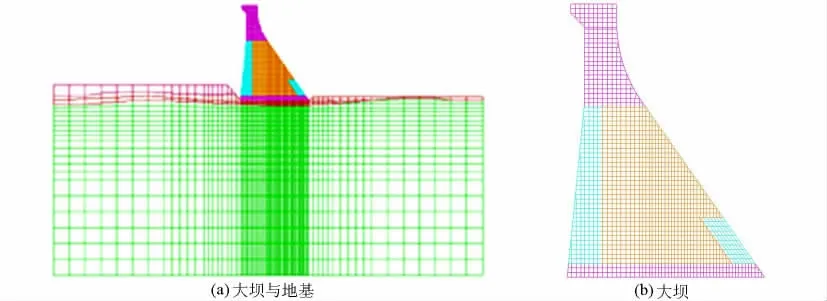
图7 大坝有限元网格Fig.7 Finite element mesh of dam model

表2 坝体混凝土材料力学参数Table 2 Mechanical parameters of concrete

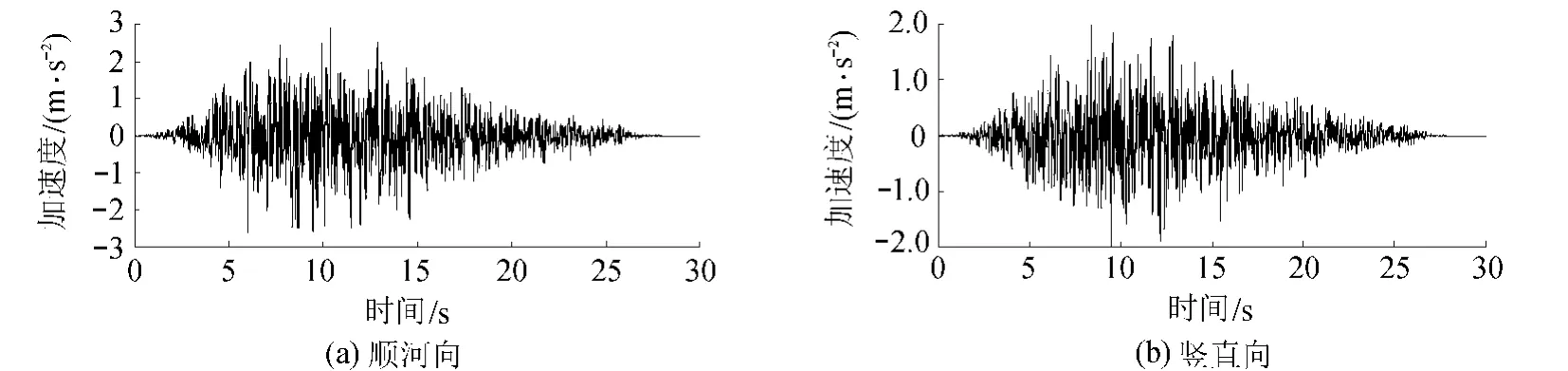
图8 地震波加速度时程曲线Fig.8 Seismic acceleration time history curves

2.4 线弹性有限元分析

坝体采用线弹性模型，在设计地震作用下，坝体顺河向加速度水平成层分布，随着坝体高程的增加逐渐增大，在坝颈部以上部分加速度放大明显，坝顶加速度最大值为15.47 m/s2，放大倍数为5.19。

图9为地震作用下坝体竖直向最大动拉应力和动静叠加后竖直向最大正应力。从图9可以看出在设计地震作用下，主要在大坝的上、下游表面产生了明显的动应力响应，竖直向动拉应力在坝踵、上游折坡处以及下游弧线段有集中，上游折坡处竖直向最大动拉应力为2.74 MPa，下游反弧段竖直向最大动拉应力为2.49 MPa。动静叠加后上游折坡处在竖直向仍有2.38MPa的拉应力，下游反弧段竖直向仍有2.16MPa的拉应力。图10给出了主拉应力超过混凝土抗拉强度的区域，可以看出在坝体上、下游折坡处有较大区域超过混凝土的抗拉强度。

2.5 非线性有限元分析

坝体采用非线性开裂模型，在设计地震作用下，坝体加速度整体分布规律与线弹性有限元计算结果基本一致，但坝体上、下游折坡处有明显不同。由线弹性有限元计算结果可知，在上游折坡以及下游反弧段部位拉应力值超过混凝土抗拉强度。在非线性计算过程中，应力超过抗拉强度的区域首先开裂，使坝体应力重分布，进而导致地震过程中裂缝随之扩展。因此，大坝坝颈部发生较大面积的开裂会导致坝颈部加速度增大。

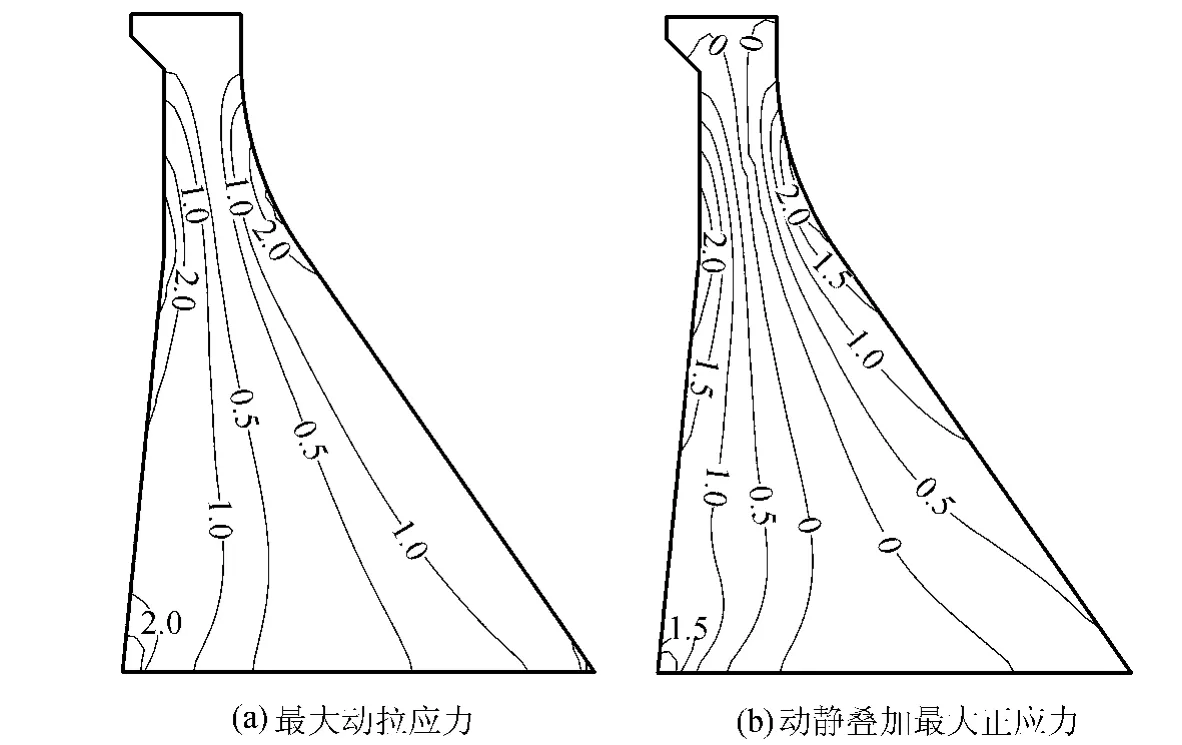
图9 坝体竖直向正应力(单位:MPa)Fig.9 Vertical stress of dam(units:MPa)

图10 主拉应力超过混凝土抗拉强度的区域Fig.10 Area with stress larger than concrete tensile strength

图11给出了考虑非线性因素后大坝竖直向最大正应力和主拉应力分布。可以看出在设计地震作用下，坝体在上、下游坝坡应力值较大，在坝踵、上游折坡处以及下游弧线段由于拉应力较大而开裂，该部位应力得到重分布。考虑非线性因素后，坝踵、上游折坡以及下游反弧段处的拉应力均小于混凝土抗拉强度，并且拉应力较大的区域向坝体内部延伸。

图12(a)为设计地震作用后大坝宏观裂纹分布。由该图可知，仅在设防地震作用下该坝段便受到了较严重的破坏，上游折坡处以及下游反弧段附近发生较大面积的开裂。在上游折坡处裂缝沿着混凝土分区的层面向下游扩展，同时在下游反弧段裂缝沿垂直于坝面的方向向上游扩展，上下游裂缝均延伸到坝体一定深度。

采用动力超载法分析大坝的极限抗震能力，图12(b)为当地震加速度峰值为0.35g，即动力超载系数为1.17时坝体宏观裂纹的分布。由该图可知上、下游裂缝在设计地震的基础上进一步向坝体内部发展，基本贯通，因此认为当动力超载系数为1.17时大坝坝颈即发生裂缝贯通性破坏，大坝抗震性能较差。

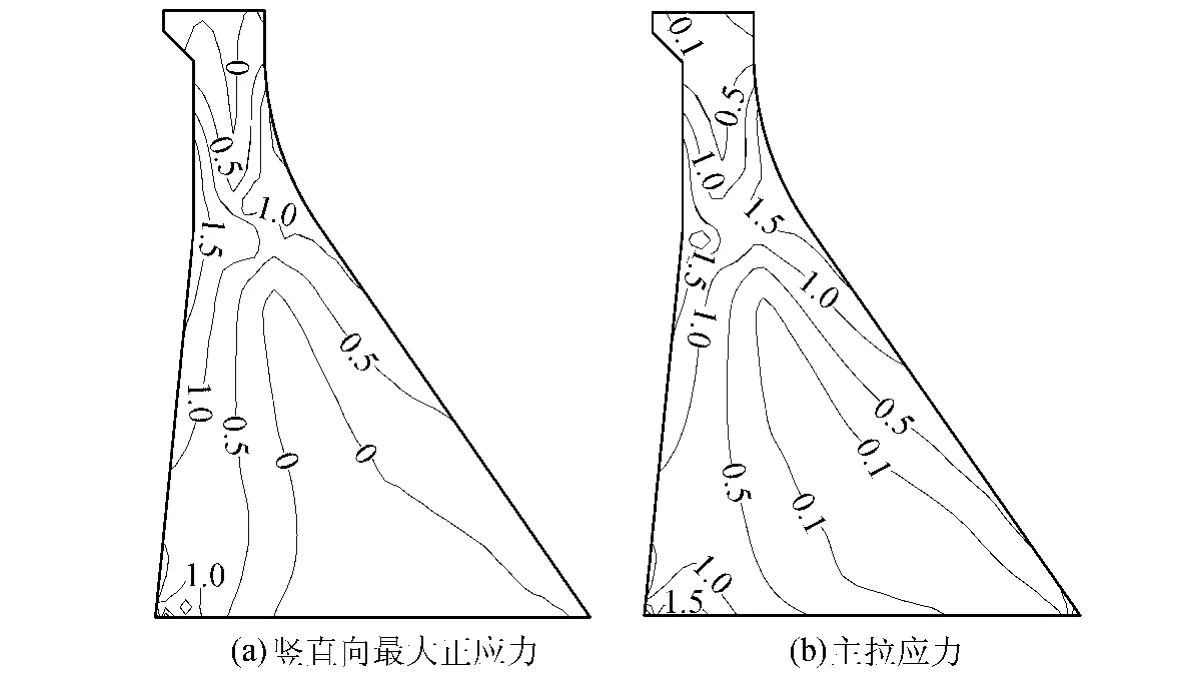
图11 重力坝最大应力分布(单位:MPa)Fig.11 Maximum stress of dam(units:MPa)

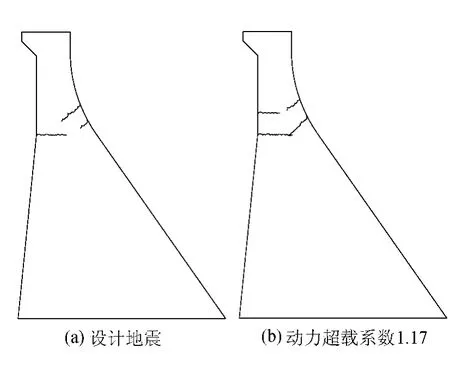
图12 地震后大坝宏观裂纹分布示意图Fig.12 Sketch map of macroscopic cracks of dam after earthquake

3 结 论

重力坝工程震害示例表明，坝颈部位在强震过程中容易出现裂缝，是抗震的薄弱部位;重力坝下游折坡点的位置对大坝抗震性能尤其是坝颈部位的抗震安全性有重要影响。通过对重力坝典型剖面下游折坡点位置进行敏感性分析，结果表明:坝颈部位应力随下游折坡点位置的降低而增大，且增大的幅度随坝高的增高而增大;为保证大坝具有良好的抗震性能，下游折坡点位置不宜太低，在8度及以上地震烈度区，高度小于100 m的重力坝折坡点位置不宜低于坝高的20%，当坝高超过100 m时除需进一步提高折坡点位置外，必要时还需采取配置抗震钢筋等抗震措施。以云南某工程为实例进行有限元分析，其线弹性计算结果表明，在设计地震作用下坝体上、下游折坡处有较大区域超过混凝土抗拉强度;非线性计算结果表明，在设防地震作用下大坝坝颈部位产生了沿上下游方向较深的裂缝，当地震超载系数为1.17时坝颈部位产生了贯穿上下游的裂缝，大坝抗震性能较差，工程设计中应合理提高下游折坡点的位置。

［1］陈胜宏，陈敏林，赖国伟.水工建筑物［M］.北京:水利水电出版社，2004.

［2］王良琛.混凝土坝地震动力分析［M］.北京:地震出版社，1981.

［3］潘家铮.重力坝设计［M］.北京:水利电力出版社，1987.

［4］朱伯芳，杨波.混凝土坝耐强震而不跨的机理［J］.水利水电技术，2009，40(1):51-57.(ZHU Bofang，YANG Bo.The reason why concrete dams can resist strong earthquakes without serious damage［J］.Water Resources and Hydropower Engineering，2009，40(1):51-57.(in Chinese))

［5］倪汉根，金崇磐.大坝抗震特性与抗震计算［M］.大连:大连理工大学出版社，1994.

［6］陈厚群.混凝土高坝强震震例分析和启迪［J］.水利学报，2009，40(1):10-18.(CHEN Houqun.Analysis on damages of high concrete dams subjected to strong earthquake and lessons for learning［J］.Journal of Hydraulic Engineering，2009，40(1):10-18.(in Chinese))

［7］徐艳杰，牟海磊，张楚汉，等.汶川地震中宝珠寺重力坝地震响应的三维有限元模拟［J］.地球物理学报，2012，55(1):293-302.(XU Yanjie，MU Hailei，ZHANG Chuhan，et al.3D finite element modeling of seismic responses of Baozhusi gravity dam in MS8.0 Wenchuan Earthquake［J］.Chines Journal of Geophysics，2012，55(1):293-302.(in Chinese))

［8］陈厚群.汶川地震后对大坝抗震安全的思考［J］.中国工程科学，2009，11(6):44-53.(CHEN Houqun.Consideration on seismic safety of dams in China after the Wenchuan Earthquake［J］.Engineering Sciences，2009，11(6):44-53.(in Chinese))

［9］GHAEMIAN M，GHOBARAH A.Nonlinear seismic response of concrete gravity dams with dam-reservoir interaction［J］.Engineering Structures，1999，21(4):306-315.

［10］GHAEMIAN M，GHOBARAH A.Seismic response of the Sefid-rud concrete buttressdam［J］.Euro Earthquake Engineering，1997(1):7-16.

［11］林皋，陈健云.混凝土大坝的抗震安全评价［J］.水利学报，2001，32(2):8-15.(LIN Gao，CHEN Jianyun.Seismic safety evaluation of large concrete dams［J］.Journal of Hydraulic Engineering，2001，32(2):8-15.(in Chinese))

［12］周星德，章青，吴继敏，等.一种提高重力坝抗震性能的方法［J］.水利水电科技进展，2011，31(3):31-33.(ZHOU Xingde，ZHANG Qing，WU Jimin，et al.Method to improve anti-seismic performance of gravity dams［J］.Advances in Science and Technology of Water Resources，2011，31(3):31-33.(in Chinese))

［13］GB18306—2001 中国地震动参数区划图［S］.