基于随机微分方程的水库防洪调度风险分析

陈 娟，钟平安，2，徐 斌

(1.河海大学水文水资源学院，江苏南京 210098;2.河海大学水资源高效利用与工程安全国家工程研究中心，江苏南京 210098)

水库防洪调度是流域洪水管理的重要内容，其各环节中都存在诸多不确定性［1-2］，包括水雨情信息采集中由于设备故障、通讯不畅、误码和量程不足等原因导致的信息无法获取或无法及时传达、信息错误，实时洪水预报中水文气象条件、模型结构、模型参数等导致的预报误差，调洪演算中的水库泄流和库容曲线等水力不确定性等。水库防洪调度中的诸多不确定性因素导致了水库防洪决策的不确定性［3-4］，因此对水库防洪调度中的不确定性因素和决策风险进行分析研究，具有学术意义和实践价值［5-7］。

目前，水库防洪调度风险分析主要有两种基本思路:数字试验法［8-10］和解析法。(a)数字试验法。首先，根据试验数据或经验判断确定防洪调度主要不确定性因素的概率分布，并采用随机模拟技术随机生成符合相应分布的各主要不确定性因素的数值;然后，用模拟生成的洪水过程进行水库调洪演算，得到模拟的防洪目标因子(水位或泄量)样本;最后，运用统计学方法分析得到在指定条件下防洪目标破坏的频率。数字试验法可以解决复杂问题的求解，但计算工作量大，计算结果的可靠性、精度与样本容量有密切关系，不能保证数值解与真值之间的一致性。(b)解析法。解析法是建立风险因子的概率密度函数，通过积分或者微分计算得到系统的风险。姜树海等［11-12］、王军［13］进行了解析法在水库防洪调度风险分析方面的研究，认为水库蓄洪量的随机变化导致了水库水位的随机消长，在假定水库蓄水量具有Wiener过程特性的前提下，推导了调洪演算随机方程，求解了调洪过程中库水位的概率密度分布。

调洪过程中不同时刻水库蓄水量的随机变化，是由入库洪水的水文条件、泄流的水力条件以及水位库容关系等不确定性因素导致的，因此笔者从这些不确定性因素出发，建立调洪演算随机微分方程，推导水库水位分布特征值与这些不确定性因素分布特征值的直接联系，并以此为依据进行水库防洪调度的风险分析。

1 水库调洪演算随机微分方程

确定性调洪演算微分方程如下:

式中:V(t)——t时刻水库蓄水量;Q(t)——t时刻入库流量;q(t)——t时刻出库流量。

在整个调洪过程中，入库洪水的水文条件、泄流的水力条件、水位库容关系的边界条件等不确定性因素导致了不同时刻水库蓄水量的随机变化，这一随机变化又将导致水库水位的随机消长，给水库水位控制造成风险。因此，采用随机过程的概念研究水库水位，有利于完整、全面地描述水位随机变化过程。本文考虑的主要不确定性因素及其数学描述如下:

a.入库洪水水文条件的不确定性。实时洪水预报中水文气象信息、模型结构、模型参数等不确定性导致了预报误差，使得预报入库洪水过程成为连续的随机过程。如果预报入库洪水过程为该随机过程的均值线，则考虑不确定性的入库流量可表述为

图1 入库流量预报误差分布示意图Fig.1 Schematic diagram of forecast error distribution of reservoir inflow

一般情况下，预报流量过程中各时段的ξ(t)是不同的(图1)，直观上认为，离作业预报时间越近，预报精度越高，预报相对误差的均方差越小，误差分布密度函数越尖瘦，预报结果接近均值的概率越大;反之，离作业预报时间越远(预见期越长)，相对误差的均方差越大，误差分布密度函数越矮胖，预报结果在均值左右较大区间变动［14］。

b.泄流水力条件的不确定性。在泄洪建筑物规模确定的情况下，受水库水位和流量系数等水力参数的不确定性影响，q(t)亦可表达为一随机过程［11-12］:

水库防洪调度一般在较高水位上进行，在高水位时C一般较稳定，因此q(t)亦可简化表达为

即泄流的不确定性主要由水位的不确定性引起。

c.水位库容关系的不确定性。由于量测、计算和绘图的误差，水库淤积和库岸坍塌等不确定性，导致了水位库容关系的不确定性。因此，与库水位H相应的水库蓄水量亦可表达为一随机过程［11-12］:

根据以上分析与假定，建立如下调洪演算随机微分方程:

式中(t)为t时刻考虑不确定性的水库蓄水量。

2 基于随机微分方程的水库防洪调度风险分析

2.1 各时刻水库水位的均值与方差推导

将式(2)代入式(6)，并进行离散得

当Δt较小时，水位变幅也较小，式(4)和式(5)可以分段拟合为如下线性关系:

式中:μt，νt——t时刻出库泄流过程的线性拟合参数;αt，βt——t时刻水位库容关系的线性拟合参数。

如图2所示，第一象限为水位库容曲线，第二象限是根据以水位为判别指标的分级防洪调度规则建立的水位与出库流量的关系线，最上部的曲线为自由泄流时的泄流能力曲线。对于任意H(t)，可以以H(t)为中心，在泄流曲线和库容曲线取两点(在泄流曲线上取点时应取同一段分段函数上的两点)，线性拟合式(8)和式(9)，进而确定 μt，νt和 αt，βt。

将式(8)、式(9)带入式(7)，整理得

图2 泄流过程和库容曲线分段线性拟合示意图Fig.2 Schematic diagram of piecewise linear fitting for discharge process and storage capacity curve

任一时刻水库水位服从概率分布，对式(10)求其均值过程，整理得

将求得的水位和水位均值带入方差公式整理得

一般情况下，经过水库调蓄，水库调洪水位的变幅比入库流量的变幅要小得多，因此可以假定各时刻入库预报流量的误差分布与水位的误差分布相互独立，即cov(H(t)，ξ(t))=0，式(12)整理得

在入流过程、泄流过程、库容曲线以及ξ(t)分布已知的情况下，可以由公式(11)和(13)计算任意时刻水位的均值和方差，进而进行调洪过程的风险分析。

2.2 水库调洪风险定义与计算

按照所建立的调洪演算随机微分方程和推导的水位特征值计算公式，可以得到任意时刻水库水位的均值和方差，假定各时刻水库水位分布可由均值和方差确定(如正态分布)，则可以得到任意时刻的水位分布(图3)。以水库水位为荷载，定义控制水位或决策者心理承受水位HR(水库实时防洪调度时，HR可根据校核洪水位和后续降雨预留防洪库容确定)［14］。定义t时刻的水库调洪风险率如下:

图3 调洪风险示意图Fig.3 Schematic diagram of risks of flood routing

式中Pt，R为t时段的水库调洪风险率。

设整个洪水过程的时段数为T，令事件H(t)＞HR为At(t=0，1，2，…，T)，定义整个洪水过程的总风险率为

假定各时段的水位分布相互独立，即事件A0，A1，…，AT相互独立，因此A0，A1，…，AT也相互独立，则

3 算 例

大伙房水库是一座以防洪灌溉为主，兼顾发电、养殖、城市供水的综合利用水库。水库总库容为22.68亿m3，汛限水位为126.40 m，设计洪水位为136.63 m，校核洪水位为139.32 m。

根据洪水预报模型对大伙房水库历史洪水进行模拟预报，统计预报入库洪峰相对误差符合正态分布N(0，0.23772)。图4为某次预报入库洪水过程，预报洪峰流量为10800m3/s，时段长Δt=1h，时段数T=130，洪峰所在时序m=55。

图4 预报入库洪水过程Fig.4 Process of forecasted reservoir inflow

由于缺乏不同时刻的误差分布信息，本文基于预报相对误差随时间线性增加的假定，按式(17)确定各时刻的误差分布:

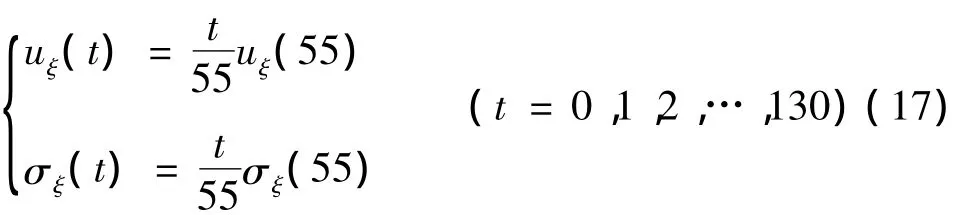
式中:uξ(t)——t时刻预报入库流量相对误差的均值;σξ(t)——t时刻预报入库流量相对误差的均方差。

由于式(11)和式(13)采用的是误差的绝对值，采用式(18)转换:

根据式(11)、式(13)逐时段递推计算得到各时段末的水位均值和方差，具体步骤如下:(a)t=0，起调水位为H(t)，E(H(t))=H(t)，D(H(t))=0;(b)以H(t)为中心(图2)，率定式(8)和式(9)中的参数 μt，νt和 αt，βt;(c)由式(18)计算E(ξ(t))和D(ξ(t));(d)将E(ξ(t))，E(H(t))，αt，μt，νt代入式(11)，得E(H(t+1));(e)将D(ξ(t))，D(H(t))，αt，μt，νt代入式(13)，得D(H(t+1));(f)如果t≥T，计算结束，否则t=t+1，转到步骤(b)。

表1 各时刻流量和水位分布特征值Table 1 Characteristic values ofreservoir inflow and water level at each moment

根据以上步骤计算各时刻水库水位均值和均方差，结果见表1。

由表1可知，随着预见期的增大，流量相对误差的均方差越大，表明洪水预报结果稳定性越差，因而随着预见期的延长，水库调度中应用洪水预报结果的风险增大。同时，调洪水位相对误差的均方差比洪水预报流量相对误差的均方差小得多，可见由于水库的调蓄作用，预报流量误差造成的风险被衰减了。

调度期内取不同的预报后续降雨值，计算后续降雨预留防洪库容，根据校核洪水位和预留防洪库容计算相应的控制水位，利用式(14)和式(16)计算整个洪水过程的调洪总风险率。由得到的控制水位值和相应的调洪风险率绘制PR～HR曲线，见图5。

由图5可见，随着后续降雨的增多，水库控制水位越低，整个洪水过程的调洪总风险率越高。已知不同的预报后续降雨值，查PR～HR曲线可求得任意控制水位下的调洪风险率，如后续降雨为80.6 mm，计算得控制水位为HR=135.60 m，查图5得到风险率为5.02%，表明整个洪水过程水位超过控制水位的总风险率为5.02%。图5在调度会商过程中可以为决策者提供必要的风险信息。

图5 不同控制水位时的调洪总风险率Fig.5 Total risKof flood routing at different control water levels

4 结 语

水库防洪调度是风险调度，不确定性因素带来了防洪决策风险，笔者就水库防洪调度中的不确定性因素对水库安全影响开展研究，取得如下主要研究成果:

a.提出了水库入库洪水、出库泄流以及水位库容关系等不确定性因素的数学描述方法。

b.基于调洪演算随机微分方程，推导了各种不确定性因素综合影响下各时刻水库水位分布均值和方差计算公式。

c.假定各时刻水库水位分布可由均值和方差确定(如正态分布)，从而得到任意时刻的水位分布，并基于此假定提出了调洪过程中各时刻的风险描述方法，以及整个洪水过程的总风险率定量计算方法。

d.以大伙房水库为背景开展了实例研究，计算结果符合水库防洪调度的实际运行状况，可用于定量评估调洪过程中任意时刻的风险和总风险，在调度会商过程中为决策者提供必要的风险信息。

［1］黄强，刘招，闫正龙，等.洪水预报信息用于水库防洪预报调度的风险分析［J］.西北农林科技大学学报:自然科学版，2008(6):200-204.(HUANG Qiang，LIU Zhao，YAN Zhenglong，et al.RisKanalysis for reservoir flood forecast operation based on flood forecast information［J］.Journal of Northwest A ＆ F University:Natural Science Edition，2008(6):200-204.(in Chinese))

［2］ ZHANG Yanping，WANG Guoli，PENG Yong，et al.RisKanalysis of dynamic control of reservoir limited water level by considering flood forecast error［J］.Science China Technological Sciences，2011，54(7):1888-1893.

［3］WU S，YANG J，TUNG Y.RisKanalysis for flood-control structure under consideration of uncertainties in design flood［J］.Natural Hazards，2012，58(1):117-140.

［4］LI Qiong，ZHOU Jianzhong，LIU Donghan，et al.Research on flood risKanalysis and evaluation method based on variable fuzzy sets and information diffusion［J］.Safety Science，2012，50(5):1275-1283.

［5］ZOU Qiang，ZHOU Jianzhong，ZHOU Chao，et al.The practical research on flood risKanalysis based on IIOSM and fuzzyα-cut technique［J］.Applied Mathematical Modeling，2012，36(7):3271-3282.

［6］钟平安，曾京.水库实时防洪调度风险分析研究［J］.水力发电，2008(2):8-9.(ZHONG Ping’an，ZENG Jing.Research on risKanalysis of reservoir real-time flood control operation［J］.Water Power，2008(2):8-9.(in Chinese))

［7］LI Xiang，GUO Shenglian，LIU Pan，et al.Dynamic control of flood limited water level for reservoir operation by considering inflow uncertainty［J］.Journal of Hydrology，2010，391(1/2):124-132.

［8］王本德，张静.基于随机模拟的分类预报调度方式风险分析［J］.水力发电学报，2009(2):8-13.(WANG Bende，ZHANG Jing.RisKanalysis on classified forecast dispatching mode based on stochastic simulative method［J］.Journal of Hydroelectric Engineering，2009(2):8-13.(in Chinese))

［9］周惠成，董四辉，邓成林，等.基于随机水文过程的防洪调度风险分析［J］.水利学报，2006，37(2):227-232.(ZHOU Huicheng，DONG Sihui，DENG Chenglin，et al.RisKanalysis on flood control operation of reservoir based on stochastic hydrological process［J］.Journal of Hydraulic Engineering，2006，37(2):227-232.(in Chinese))

［10］朱元甡.基于风险分析的防洪研究［J］.河海大学学报:自然科学版，2001，29(4):1-8.(ZHU Yuanshen.Flood defense based on risKanalysis［J］.Journal of Hohai University:Natural Sciences，2001，29(4):1-8.(in Chinese))

［11］JIANG Shuhai.Application of stochastic differential equations in risKassessment for flood releases［J］.Hydrological Sciences Journal，1998，43(3):349-360.

［12］姜树海，范子武.水库防洪预报调度的风险分析［J］.水利学报，2004，35(11):102-107.(JIANG Shuhai，FAN Ziwu.RisKanalysis for flood control operation of reservoir［J］.Journal of Hydraulic Engineering，2004，35(11):102-107.(in Chinese))

［13］王军.基于贝叶斯理论的洪水实时预报调度研究［D］.南京:河海大学，2010

［14］钟平安.流域实时防洪调度关键技术研究与应用［D］.南京:河海大学，2006.