基于空间压缩理论的粒子群算法在输电网规划中的应用
崔德义
(上海市电力公司嘉定供电公司,上海 201800)
电网规划是指在给定的电源规划和负荷预测基础上,对现有的线路结构进行新增或扩建,以满足电力系统安全、可靠的运行。从数学上讲,此类问题属于带有多约束条件,无法用固定公式来求解的非线性问题。因此,一般采用现代启发式算法[1],比如遗传算法(GA)[2],粒子群算法(PSO)[3],蚁群算法(ACO)[4]等进行求解。其中粒子群算法实现简单,具有较快的计算速度与较好的并行计算能力,并且对问题的初始约束条件要求不高,所以被广泛应用于电网规划中。
粒子群算法来源于对简化社会模型的模拟,利用记忆机制分别记录全部粒子和各粒子自身的最优适应度值,通过反馈和学习机制逐渐使得粒子向最优解方向移动[5]。与遗传算法相比,没有变异过程,而是通过粒子之间的竞争和学习来优化计算结果。同时,更新后的粒子容易受局部最优解的吸引,使算法过早收敛。很多学者,比如Eberhart[6]等通过增加一个惯性权重系数来改变搜索空间的范围以优化计算结果,但实际效果并不明显。
当粒子维数在10维以内时,粒子群算法收敛效果较好[7],但随着粒子维数的不断提高,即使加入惯性权重系数也无法得出满意的全局最优解。本文根据电网规划独有的特性,引入空间压缩理论,解决了过早收敛问题并最终改善了优化结果。
1 电网规划基本算法模型
1.1 更新和选择最优粒子
电网规划的具体研究对象是线路走廊中的线路回数,因此设每个粒子中的第k维变量的值即为第k条线路走廊的线路回路数。对于需要规划具有D条线路走廊的问题,设粒子维数为D维,假设共有m个这样的粒子,则粒子可表述为:

每个粒子值配置初始速度为:

引入学习机制对随后的粒子进行更新[8],计算式为:

式中:r1,r2分别为均匀分布在0~1之间的随机数;c1为自我认知权重,c2为学习权重,两值分别表征了粒子群自我认知程度和向当前全局最优粒子学习的程度。一般设为2。
1.2 确定目标函数
对于实际运行的网络规划模型,需确定一个目标函数用来计算适应度值,以判别和。一个考虑网络投资费用和网络运行损耗费用的目标函数可表述为:
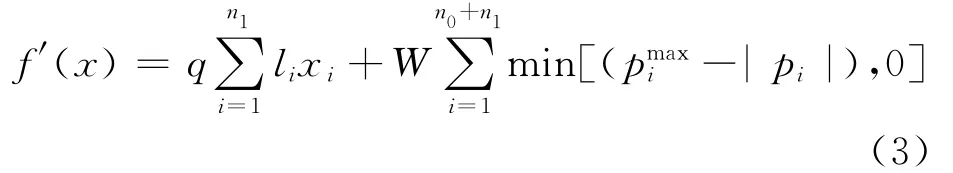
式中:n0为电网已有的固定线路走廊;n1为允许架设线路走廊;xi为允许新增的第i条线路走廊中的线路回路数;li为第i条线路长度,用来表征线路架设费用;Pi为实际运行过程中第i条线路上流过的功率;Pmixi为第i条线路所允许通过的最大功率。
当线路过负载,即|Pi|->0时,第二项通过乘上一个惩罚因子W 来使整个目标函数值f′(x)变大。显而易见,目标函数值f(x)越小,表示网络投资和电网运行费用越小,其所代表的网络规划配置就越好。
需要注意,若某个粒子中0值过多,可能会使输电网络产生孤立节点,因此对每一次新生成的网络图需要进行判断。当网络出现孤立节点时,直接赋予适应度函数一个很大的值,这样避免了不必要的计算。最终将整个适应度函数表达式改为:

式中:U为一个很大的罚值,可直接取为W的100倍。
如何判断一个输电网络是否存在孤立节点,可利用拓扑搜索法来解决,主要通过判断是否满足收敛条件来确定计算是否终止。一是粒子在更新数次后,其全局最优适应度值不发生变化,则认为满足收敛条件,计算终止;二是每一次更新粒子群计算得到全局最优适应度函数值与前一次所得的全局最优适应度函数值之差小于给定值ε时,即认为满足收敛条件,计算终止。经过计算证实了,在足够多的粒子下(一般设定粒子数为维数的7~10倍),粒子更新20次后,其最优适应度值一般不会再发生变化[9]。整个算法流程如图1所示。

图1 粒子群输电网规划流程图
实践表明,传统的粒子群算法虽然实现简单,但实际优化效果并不理想,原因是粒子很容易受局部最优解的影响[6],即使增加迭代次数,也会继续被上一代的局部最优粒子吸引。现利用传统粒子群算法,对一个具有18节点27条线路走廊的网络进行规划,其算法收敛效果如图2所示。

图2 传统粒子群算法收敛效果图
分别对50个,100个,500个粒子进行计算,结果表明,在粒子更新至20~25次后,其适应度值已经趋于平稳,其值分别在56 219,53 533,51 238元左右,而此18节点系统的标准最优适应度函数值为4.5万元,即使粒子数选择为500个,迭代次数选择为30次,其计算结果也与标准结果相差11.11%,可见实际优化效果并不理想。
从图2也可以看出,为了更快地找到最优解,通过增加初始粒子数目比增加粒子更新次数所得到的效果更好。对于粒子数目为500的算法模型,其第一次计算的结果就比粒子数目为50个,迭代次数为30次的效果要好。大量实验证明,只需粒子更新20次左右,其结果就趋于某个局部最优解,盲目的增加粒子更新次数只会增加计算时间,对最优解的搜寻没有任何帮助。
2 改进粒子群算法
2.1 基本原理
现结合输电网规划的实际情况,通过引入空间压缩机制的改进粒子群算法来提高收敛效果。考虑到粒子更新20次左右时将会收敛到某一局部最优解,可将某一初始粒子采用传统粒子群算法迭代30次(这样保证能够收敛到某一局部最优解),之后若能保证新生成的粒子能产生比前一粒子更优秀的目标函数值,那么计算效果会得到很大提高。为了便于分析,仅考虑粒子维数为二维的情况,如图3所示。

图3 二维粒子变异机制图解
由图3可知,全部粒子的搜索空间为整个坐标的第一象限,对于1个仅设有2条线路走廊的输电网规划模型,即1个二维的粒子(x1,x2),假定经过一定次数的更新后,粒子最优可行解收敛到(a,b)点,目标函数为f(a,b),则以(a,b)坐标为中心点的右上角网格阴影部分(包括边界线)有任意x1≥a, x2≥b,物理意义为任意取值在网格阴影部分中的粒子,其线路走廊的规划线路回路数总是大于或者等于(a,b)这种规划方案,但由于增加线路回路数会增加投资成本,所以对于任意x1≥a,x2≥b所表示的网络投资都会增加。由此可知,随机搜索在网格范围内的所有粒子值可以不予考虑,而所有新生成的粒子理应在网格范围之外(不包括边界线)生成。这样,整个粒子的搜索范围被压缩了一部分,这就是空间压缩的基本原理。
2.2 最优可行解的效率分析
改进粒子群算法中,每次得出的新粒子在压缩之后的空间范围内总能找到更优解,并且随着新粒子不断的更新和空间的不断压缩,使得搜索全局最优可行解的概率越来越大,其搜索效率可用图4表示。

图4 空间压缩和全局最优解的搜寻
由图4可知,通过第一次算得的f(a1,b2)值确定网格区域1,然后使粒子(x1,x2)的第二次更新范围在区域1之外产生,而再次计算得到的适应度值f(a2,b2)又继续会将整个搜索空间进一步压缩。这样,第三次生成的粒子(x11,x12)值会在区域1和2之外产生,因此已被压缩空间的有效搜索范围被进一步缩小。重复以上步骤,随着新的局部最优解不断被找到,搜索空间也随之不断的被压缩,粒子群的搜索效率也会越来越高并最终逼近最优解。而之前得到的所有局部最优解所对应的规划方案(f(a1,b2)和f(a2,b2))亦可作为输电网规划的参考方案。
2.3 收敛判据
改进粒子群算法使得计算效率明显提高,新生成的粒子保证其目标函数值一定比之前得到的最优解更好,避免了无效粒子的生成。其算法终止判定条件为在一定的迭代次数内,更新后的粒子算得的最优适应度值,与之前生成的最优适应度值相等时计算结束。
3 算例分析
3.1 两种算法的分析
将上节的算例用引入空间压缩机制的改进粒子群算法重新计算,计算结果如图5所示。
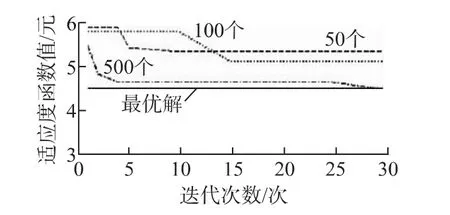
图5 改进粒子群算法收敛效果图
改进后的目标函数收敛效果在粒子数目分别为50个,100个,500个计算时,其目标函数适应度值,分别比传统粒子群算法提高了16.67%,9.10%和11.11%,优化效果明显。
3.2 规划网络图的分析
对于以上算例,采用传统粒子群算法,设定初始粒子数为200个,迭代计算为600次,得到的规划结果如图6所示。

图6 传统粒子群算法规划网络图
图6中粗实线为输电线路已有固定线路,不参与计算。在满足约束条件的前提下,图6总共新增22条线路。跟踪发现,当迭代至第25次时,算法已经收敛,之后新生成的粒子总会被此局部最优解所吸引。也就是说,之后的575次计算结果与第25次的计算结果一致,为无效计算。
现采用改进粒子群算法,同样设定初始粒子数为200个,迭代次数为30次后找到相应局部最优解并进行空间压缩,再在新的压缩空间里进行计算,按此法循环20次,总计算次数仍然为600,得出的结果如图7所示。
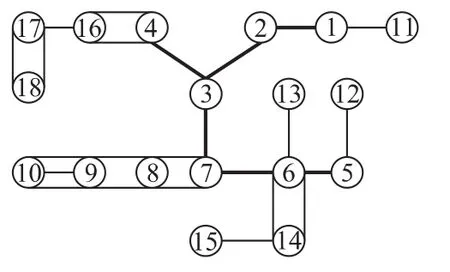
图7 改进粒子群算法规划网络图
由图7可知,只增加了18条线路,即满足了所有约束条件并保证线路不过载,而且投资费用大大减少。在相同初始条件和迭代次数下改进粒子群算法优化效果明显。实际结果表明,图7亦即为该18节点算例的全局最优解。
4 结语
基于空间压缩的改进粒子群算法在应用中具有三大优点。一是,每次更新计算时的粒子群总是在压缩后的空间中产生,提高了粒子搜索效率,对于1个18节点的具体算例,在相同的初始粒子群数目和计算次数之内,平均算法优化效果可提高15%左右。二是,不同于传统算法中粒子群更新的盲目性,改进粒子群算法的新粒子搜索空间总在可能产生更优适应度值的搜索范围内,避免了重复计算。三是,每次更新后的粒子找到的局部最优可行解都可为规划方案提供参考,增加了规划的灵活性。
当然,改进粒子群算法还需要进一步完善:比如,对于每次在压缩空间以内进行搜索的粒子,若粒子数目选择的不够大,容易使更新后的粒子所对应的网络发生过负荷或者产生孤立节点,进而导致目标函数会非常大(由罚函数造成),反而使计算结果发散,需要对此情况引起高度重视,予以判别并且加以改进。再比如,进一步完善空间压缩理论,考虑增加网络线路过负荷约束条件的序特性,使图3以(a,b)点为原点的网络第三象限部分也予以屏蔽,可以进一步增加压缩范围,提高搜索效率。
[1] 金义雄,程浩忠,严健勇,等.现代启发式算法及其输电网络扩展规划中的应用[J].华东电力,2005,33(8)19-25.
[2] 玄光男,程润伟,等.遗传算法与工程优化[M].北京:清华大学出版社,2004:1-3.
[3] 纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009:16-19.
[4] 段海滨,马冠军,等.一种求解连续空间优化问题的改进蚁群算法[J].系统仿真学报,2007.19(5):974-977.
[5] 李丽,牛奔.粒子群优化算法[M].北京:冶金工业出版社,2009:25-34.
[6] Shi Y,Eberhart R C.A Modified Swarm Optimizer[A].IEEE International Conference of Evolution Computa-tion[C].Anchorage,Alaska:IEEE Press,1988:69-73.
[7] 曾健潮,介婧,崔志华.微粒群算法[M].北京:科学出版社,2004:15-18.
[8] 金义雄,程浩忠,严健勇,等.改进粒子群算法及其在输电网规划中的应用[J].中国电机工程学报,2005,25(4):46-50.
[9] 金义雄,程浩忠,严健勇.基于局优化分支优化的粒子群收敛保证算法及其在电网规划中的应用[J].电机工程学报,2005,25(23):12-18.

