微地震信号到时自动拾取方法

刘劲松，王 赟，姚振兴

1中国科学院地质与地球物理研究所，北京 100029 2中国科学院地球化学研究所，贵阳 550002

1 引 言

近年来美国大规模的页岩气开采引发了各国对页岩气资源的关注.我国致密砂岩油气藏和页岩气藏资源丰富，在松辽、鄂尔多斯、四川及南方诸多盆地均有分布［1］，这些致密砂岩油气藏和页岩气藏的天然气资源将成为我国重要的能源支柱.对致密砂岩油气藏和页岩气藏主要采用水平井分段水力压裂技术方式开采.水力压裂使地层形成新的裂缝，产生微震.监测微地震的分布和特征可为水力压裂设计和压裂效果的监测提供依据，提高开采效益［2－6］.

微地震记录的特点是频率高、信噪比低，因此微地震事件的自动识别和初至到时拾取对实现海量微地震数据的自动处理有重要意义［7］.对于天然地震事件，已提出了多种自动识别方法.这些方法主要根据在地震记录中地震事件到达前后质点振动性质差别构建特征函数加以判断.例如，根据在时间域能量和 能 量 变 化 构 建 特 征 函 数，Allen［8－9］、Baer和Kradolfer［10］提出了长短时均值比方法（STA／LTA法）；根据在时间－频率域能量变化，Gibbons等［11］提出了频谱比方法；根据地震信号到达前后地震波形数据统计性质的差别，Maeda［12］提出了AIC方法，Saragiotis［13］提出了基于地震波形偏斜度和峰度的PAI－S／K方法；以及常旭和刘伊克［14］讨论的分形分维方法等.王继等［15］讨论了用AIC方法对流动地震台阵观测记录初至震相的自动检测问题.与天然地震的记录相比，微震的震级更小，通常在1级以下，而且信噪比更低，有必要深入地讨论这些方法对微地震事件的识别问题.

本文利用STA／LTA、AIC和PAI－S／K方法，采用两种时窗，并利用全局优化搜索方法选取拾取的控制参数，对在我国西部某地观测到的震中距范围在0.3至20km、震级范围－0.5至1级的约13359个微震记录进行初至到时拾取，比较了上述三种方法的优缺点，提出了相应的改进方法，以利于今后的微震监测工作.

2 地震信号到时自动拾取的几种方法

2.1 长短时均值比（STA／LTA）方法

Allen［8－9］提出的STA／LTA方法，是目前广泛使用的一种地震信号到时自动拾取方法，其主要原理是根据地震波形特征函数的长短时均值，以及地震波形过零轴的次数统计等特征拾取初至，原理如下：

设di，i＝0，1，2，…，n－1为离散地震波形数据，fi为高通滤波后的数据：

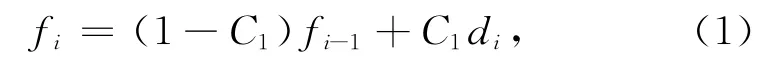
根据质点振动的能量和能量变化定义特征函数Ei为

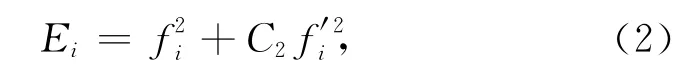
其中f′i为fi对时间的导数，C2为常数.特征函数的短时均值函数αi和长时均值函数βi定义为

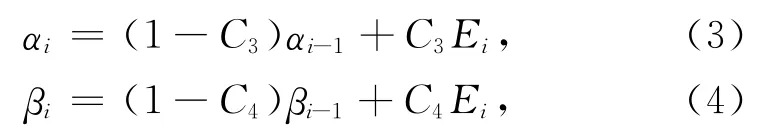
振幅绝对值的平均值eabsi定义为：

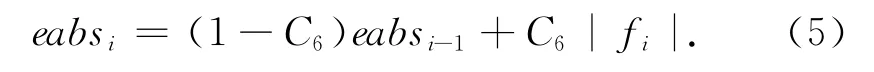
判定初至的准则是同时满足下列条件［8］：

（1）αi≥C5βi，eabsi≤C7，并且后续的波形同时满足下列条件；

（2）总过零次数（mzc）大于等于I4，或者，连续小振幅过零次数大于等于I3＋mzc／I3；

（3）大振幅过零次数大于等于I6并且总过零次数大于等于I4，或者，当前时刻距满足条件1的时刻大于等于D5.

以上C1－C8以及I3、I4、I5等为常数.SAC软件系统［16］含有STA／LTA方法的功能模块（apk命令，pkdet等相关函数），SAC软件建议的缺省值如表1所示.

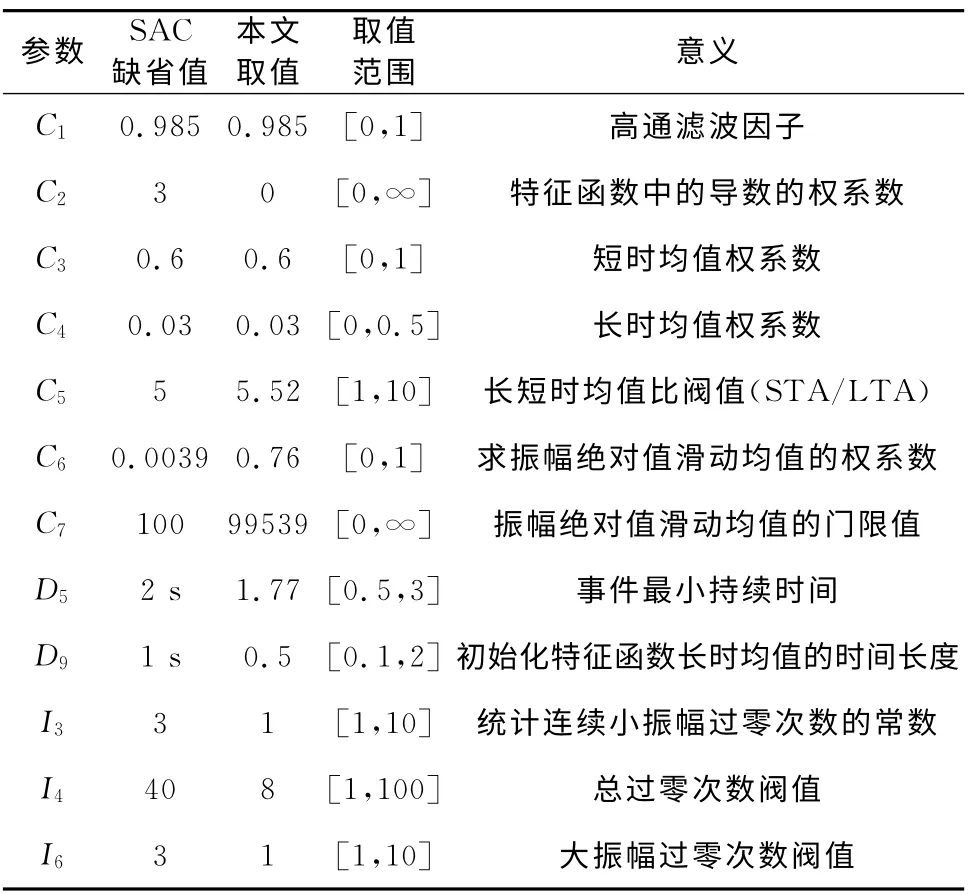
表1 STA／LTA方法参数意义及取值Table 1 Parameters of STA／LTA method

2.2 AIC方法

该方法的基本原理是求取地震信号AIC函数局部最小值的位置.AIC函数定义为［12，15］：

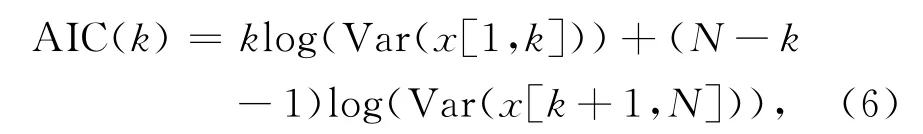
其中｛xi｝，i＝1，2，3，…，N为地震信号的离散波形序列.

在时窗正好包含了地震信号前后一段波形的情况下，AIC函数在初至点峰值尖锐，准确率较高.但AIC函数受时窗的影响较大，在不同的时窗下，其局部最小值出现的位置往往不同，如图1所示.因此该方法适用于已知初至的大致位置的情况.

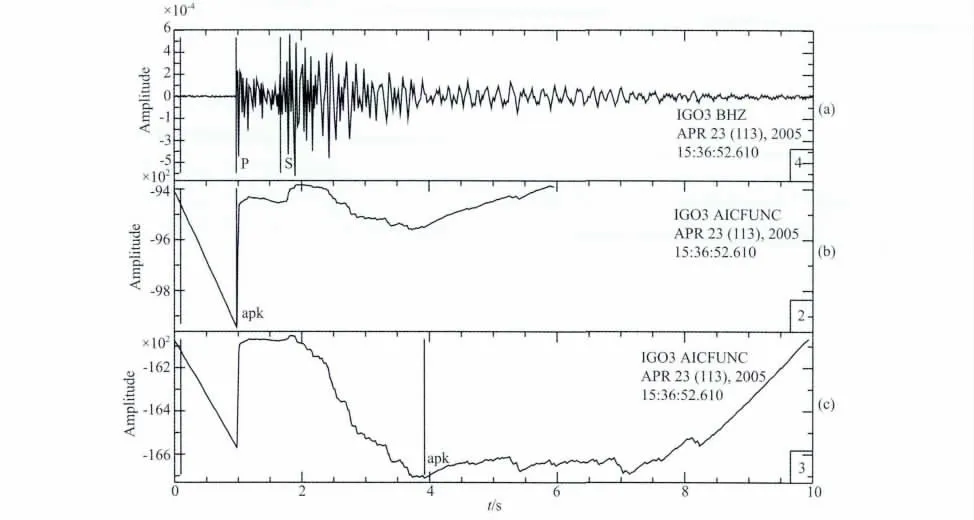
图1 （a）一个地震信号的垂直分量波形；（b）时窗采用初至前1s至初至后3s的AIC函数；（c）时窗采用初至前1s至初至后9s的AIC函数Fig.1 Vertical component of an earthquake signal（a）and its AIC function of time window from 1second before onset to 3second after onset（b），and AIC function of time window from 1second before onset to 9seconds after onset（c）

2.3 基于高阶统计量偏斜度和峰度的PAI－S／K方法

2002年，Saragiotis提出了基于地震波形峰度和偏斜度的拾取初至方法，称之为PAI－S／K方法［13］.对于一个有限长度的离散实数序列｛xi｝，其偏斜度S（skewness）和峰度K（kurtosis）定义为：

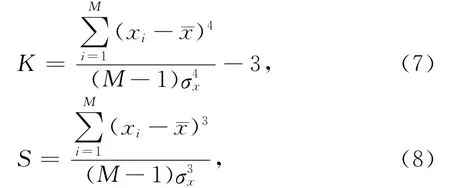
其中为｛xi｝序列的平均值，σx为其标准差.

利用地震波形峰度和偏斜度检测地震波到时的基本原理是判断峰度曲线和偏斜度曲线的极值点，以极值点前曲线斜率最大的位置作为地震波到时的位置，该方法具有计算稳定强健、实现简单等优点.图2为一个地震记录及其峰度和偏斜度曲线.

3 实际数据的拾取结果

本文应用上述方法，对我国西部某地的13359条微地震观测数据记录进行了初至到时自动拾取，同时人工拾取了P波到时和S波到时.数据涉及1600多个微地震事件，绝大多数的地震震级小于1，震中距范围从0.3km到20km左右.自动拾取采用两种时窗，时窗1为［tp－3，tp＋2tps］，即P波初至前3s至初至后2倍纵横波走时差，该时窗包含了P波初至和S波初至.时窗2为［tp－3，tp＋tps］，该时窗起始于P波初至前3s，终止于S波开始时刻，未包含S波.时窗1对应于一般情形，实际数据处理中多数为这种情况.时窗2对应已知初至大致位置的情况，例如流动地震观测中的远震.拾取前对数据进行了5～30Hz的带通滤波.

对于STA／LTA方法，首先采用SAC软件的缺省参数进行拾取，自动拾取的初至与人工拾取的初至时差在0.3s以内的记录约占55%，时差在0.1s以内的约占54%.由于SAC软件中建议的缺省参数是针对天然地震的，其震级相对较大，对于微地震的情况，这些参数可能不是最佳的.为得到最佳的参数，本文采用DE全局搜索方法［17］，以人工拾取的初至作为参照，以时差在0.3s以内的记录所占百分比作为目标函数，自动搜索最佳的拾取参数.得到的结果是，小于0.3s的记录可增加到77.1%，如表2所示.最佳参数见表1的第3列.从所求得的最佳参数表明，至少对于本文所用的数据，在特征函数中加入导数项，其效果不如仅采用振幅平方作为特征函数.

AIC方法的拾取结果如表2所示.结果表明，在时窗2的情况下，AIC方法是本文讨论的几种方法中准确率最高的方法.由AIC函数的计算公式可知，某个点上的AIC函数值，依赖于搜索时窗内每个点的值，当搜索时窗变化时，对应波形某特定点上的AIC函数值也是不同的，因此AIC方法不适合沿连续地震记录滑动进行.

PAI－S／K方法的拾取结果见表2的第3～4行.Saragiotis［13］用该方法对44个区域地震范围的地震信号记录进行了自动拾取，并与STA／LTA方法的结果进行了对比，其结论是该方法优于STA／LTA方法.但从本文的实际数据拾取结果看，在时窗1的情况下该方法拾取的准确率不如采用优化参数后的STA／LTA方法.PAI－S／K方法通过判断搜索时窗内的最大值点确定初至位置，因而拾取结果也受搜索时窗范围的影响.该方法只有一个控制参数，即计算峰度和偏斜度的滑动时窗长度.同样采用DE全局搜索方法，可得到对于本文实际数据最佳的滑动时窗长度.对于偏斜度，最佳滑动时窗长度为2.70s，对于峰度，最佳滑动时窗长度为0.72s.滑动时窗长度对结果也有一定影响，但在一定变化范围内，对拾取结果的影响不大.例如，对于峰度法，当滑动时窗长度在［0.5，1.5］之间变化时，与人工拾取结果在0.3s以内的结果所占百分比的变化在1个点左右.

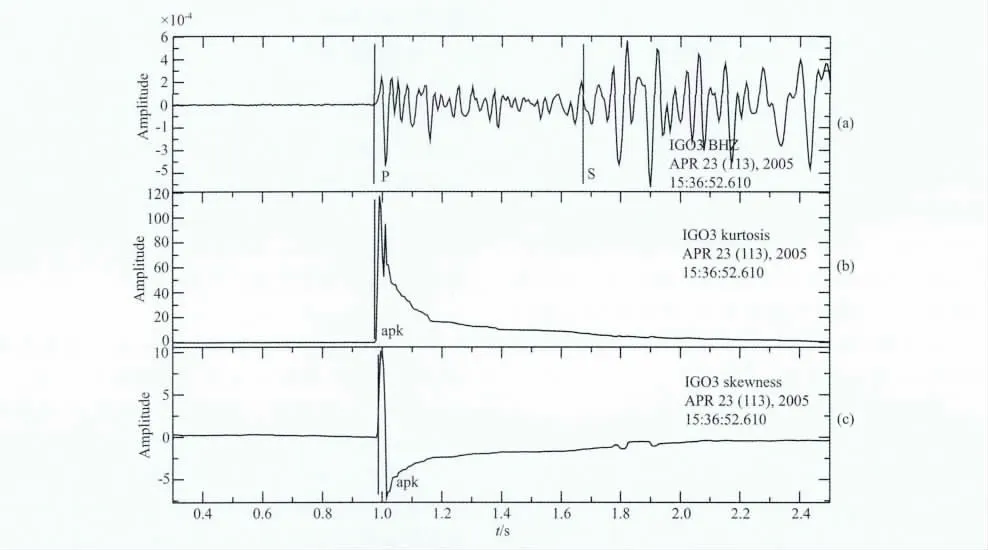
图2 一个地震记录波形（a）及其峰度（b）和偏斜度曲线（c）Fig.2 An earthquake signal（a）and its kurtosis（b）and skewness（c）curves

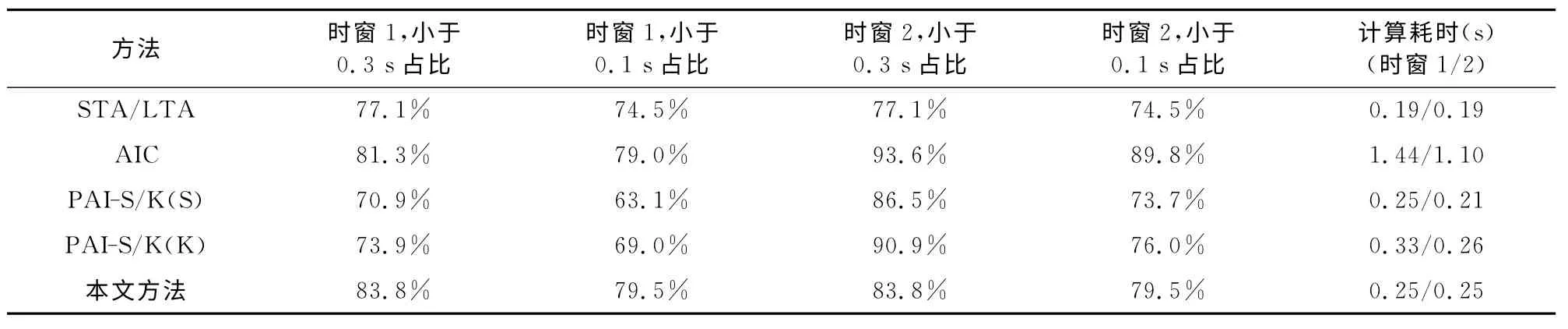
表2 各种方法初至拾取情况一览表（表中计算耗时未计入硬盘IO时间）Table 2 Picking results of each method（the IO operation time is not included in time consumption）

4 对PAI－S／K方法的改进

4.1 移动时窗峰度的快速算法

对于一个长度为N的地震波形序列｛xi｝，设求峰度的时窗长度为M，按照公式（7）沿地震波形滑动求取峰度，要调用（N－M）次公式，计算量为O（M·（N－M）），对于海量的多道连续观测记录，其计算效率较低.本文将上述公式展开，将公式变换为求取离散实数序列的算术和、平方和、立方和、4次方和的线性组合形式，减少重复计算，计算量减少为O（N），极大地提高了计算效率.

将（7）式展开并变换得到：

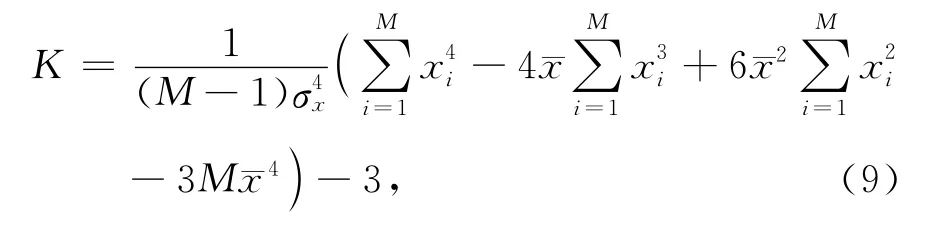
将时窗内离散序列的算术和、平方和、立方和、4次方和分别记为smj，j＝1，2，3，4，得到：

采用（10）—（12）式计算的优点是，当时窗移动时计算新时窗的smj不必重复计算时窗内所有点的值，只须在上一个时窗各值的基础上，加上新进入时窗的值，并减去离开时窗的值即可.经实际数据计算测试，在时窗长度取0.5s、1.0s、1.5s的情况下，采用快速算法的计算速度分别提高了22倍、32倍、43倍.对于偏斜度以及AIC函数的计算，同样可采用类似的方法提高速度.

4.2 到时判别算法

原方法采用峰度最大值点左侧斜率最大的点作为初至位置，但实际数据的结果显示，该点往往滞后于真实的初至位置，而峰度曲线开始起跳的位置更接近初至位置.在某些情况下，初至附近的峰度极值点也不是最大值点.针对这些情况，本文将STA／LTA方法与PAI－S／K法结合，以地震波形的峰度K作为特征函数，以特征函数的长短时均值比和峰度值作为判断初至位置的依据.具体方法如下：

定义特征函数Ei为

其中Ki为第i个样点处的峰度，Ki的值由第i个样点前M个地震波形数据计算.与STA／LTA的方法类似，短时均值函数αi和长时均值函数βi定义为：

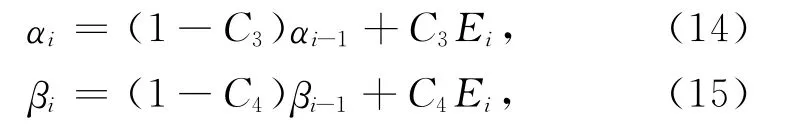
满足下列条件的位置判定为初至：

（1）αi≥C5βi并且αi≥C6；

（2）满足条件1的位置记为n，由n开始向前（时间减小方向）搜索Ki的值，直到满足Ki≤Ki－1.

图3为一个地震记录的波形和峰度、以及峰度的长短时均值曲线，图4为初至附近的局部放大图.

上述公式中的C3—C6为常数.将上述方法应用于本文的实际数据，同样采用DE全局搜索法搜索最佳参数，保持C3＝0.6，C4＝0.03不变，以人工拾取的初至作为参照，以时差在0.3s以内的记录所占百分比作为目标函数，自动搜索最佳的C5和C6的值以及滑动时窗长度.对于本文的数据当C5＝2.71，C6＝1.43，滑动时窗长度为0.79s时，自动识别的效果最佳，得到的结果如表2中所示.从表2可以看出，在时窗1的情况下，识别准确率比原PAI－S／K方法提高了约10个百分点，比STA／LTA方法提高了约5个百分点.

本方法主要有两个参数C5和C6，分别是长短时均值比阀值和峰度值短时均值的阀值.在P波初至附近的极值点处，长短时均值比和极值都随地震信号的信噪比增加而增加，峰度的极值尤其明显.根据（7）式和（8）式，偏斜度和峰度均为无量纲量，因而对于不同类型的地震记录（速度、加速度、不同的仪器增益等），该方法的拾取参数具有一定的普遍意义.

5 结 论

本文通过地震信号初至拾取STA／LTA方法、AIC方法和PAI－S／K方法的讨论，以及我国西部某地13359条微震实际数据的自动拾取与人工拾取结果对比分析，可以获得如下认识：

STA／LTA法历史悠久，算法稳定强健，目前仍被广泛使用.该方法可沿地震记录波形滑动进行，因而可用于地震信号的检测，但该方法涉及参数较多，不易掌控.

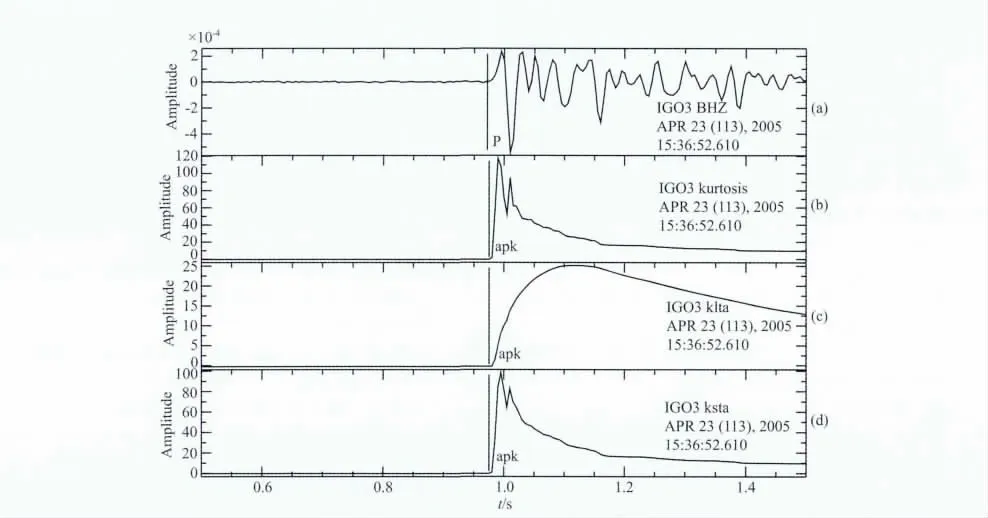
图3 （a）—（d）分别为：垂直分量地震记录波形，地震波形的峰度曲线，峰度曲线的长时均值，峰度曲线的短时均值Fig.3 From（a）to（d）are an earthquake signal and its kurtosis，long time average of kurtosis，and short time average of kurtosis curves，respectively

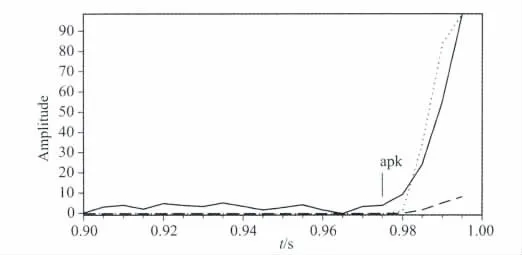
图4 图3中初至附近的波形（实线）、峰度曲线长时均值（虚线）、短时均值（点线）.波形曲线按照峰度曲线做了归一化处理.Fig.4 The enlarged part of Fig.3near onset.Solid line，dashed line and dotted line represent waveform，LTA curve and STA curve of waveform respectively.The waveform curve is rescaled according to kurtosis curve.

AIC方法在时窗正好包含了地震信号前后一段波形的情况下，能够得到非常好的结果，适用于已有震源先验信息的情形，例如流动地震观测中记录到的远震信号和区域地震信号，以及在已经用其它方法检测出地震信号所在时段后，再应用AIC方法判断到时.

PAI－S／K方法原理简单实现容易，算法同样稳定强健，由于该方法采用了高阶统计量判断信号初至，具有一定的抗干扰能力.

本文提出的改进后的PAI－S／K法，可方便地沿连续地震记录波形滑动进行，因而可用于地震信号的检测，在时窗1的情况下，小于0.3s的记录占比达到83.8%，是上述方法中最高的；该方法涉及的参数较少，同时由于峰度的无量纲特性，因而所涉及参数的选取具有一定的普遍性.

（

）

［1］ 张金川，徐波，聂海宽等.中国页岩气资源勘探潜力.天然气工业，2008，28（6）：136－142.

Zhang J C，Xu B，Nie H K，et al.Exploration potential of shale gas resources in China.NaturalGasIndustry（in Chinese），2008，28（6）：136－142.

［2］ 赵金洲，王松，李勇明.页岩气藏压裂改造难点与技术关键.开发工程，2012，32（4）：1－4.

Zhao J Z，Wang S，Li Y M.Difficulties and key techniques in the fracturing treatment of shale gas reservoirs.NaturalGas Industry（in Chinese），2012，32（4）：1－4.

［3］ 刘振武，撒利明，杨晓等.页岩气勘探开发对地球物理技术的需求.石油地球物理勘探，2011，46（5）：810－820.

Liu Z W，Sa L M，Yang X，et al.Needs of geophysical technologies for shale gas exploration.OilGeophysical Prospecting（in Chinese），2011，46（5）：810－820.

［4］ 张山，刘清林，赵群等.微地震监测技术在油田开发中的应用.石油物探，2002，41（2）：226－231.

Zhang S，Liu Q L，Zhao Q，et al.Application of microseismic monitoring technology in development of oil field.GeophysicalProspectingforPetroleum（in Chinese），2002，41（2）：226－231.

［5］ 王爱国，周瑶琪，陈勇等.基于微地震技术的油田裂缝监测及模拟.中国海洋大学学报，2008，38（1）：116－120.

Wang A G，Zhou Y Q，Chen Y，et al.Monitoring and simulation of fracture in oil field based on micro－seismic technology.PeriodicalofOceanUniversityofChina（in Chinese），2008，38（1）：116－120.

［6］ Duncan P M，Eisner L.Reservoir characterization using surface microseismic monitoring.Geophysics，2010，75（5）：139－146.

［7］ Warpinski N.Microseismic monitoring：inside and out.JournalofPetroleumTechnology，2009，61（11）：80－85.

［8］ Allen R V.Automatic earthquake recognition and timing from single traces.Bull.Seismol.Soc.Amer.，1978，68（5）：1521－1532.

［9］ Allen R V.Automatic phase pickers：their present use and future prospects.Bull.Seismol.Soc.Amer.，1982，72（6）：225－242.

［10］ Baer M，Kradolfer U.An automatic phase picker for local and teleseismic events.Bull.Seismol.Soc.Amer.，1987，77（4）：1437－1445.

［11］ Gibbons S J，Ringdal F，Kværna T.Detection and characterization of seismic phases using continuous spectral estimation on incoherent and partially coherent arrays.Geophys.J.Int.，2008，172（1）：405－421.

［12］ Maeda N.A method for reading and checking phase times in auto－processing system of seismic wave data.Zisin＝Jishin，1985，38（3）：365－379.

［13］ Saragiotis C D.PAI－S／K：A robust automatic seismic P phase arrival identification scheme.IEEETransactionson GeoscienceandRemoteSensing，2002，40（6）：1395－1404.

［14］ 常旭，刘伊克.地震记录的广义分维及其应用.地球物理学报，2002，45（6）：839－846.

Chang X，Liu Y K.The generalized fractal dimension of seismic records and its application.ChineseJ.Geophys.（in Chinese），2002，45（6）：839－846.

［15］ 王继，陈九辉，刘启元等.流动地震台阵观测初至震相的自动检测.地震学报，2006，28（1）：42－51.

Wang J，Chen J H，Liu Q Y，et al.Automatic onset phase picking for portable seismic array observation.Acta SeismologicaSinica（in Chinese），2006，28（1）：42－51.

［16］ 彼得·鲍曼.新地震观察实践手册.中国地震局监测预报司译.金严，陈陪善，许忠淮校.北京：地震出版社，2006.

Peter B.New Manual of Seismological of Observatory Practice（in Chinese）.Beijing：Seismological Press，2006.

［17］ Storn R，Price K.Differential evolution－a simple and efficient adaptive scheme for global optimization over continuous spaces.Technical Report TR－95－012，ICSI，1995.