连续随机变量函数概率密度的辅助随机变量解法

汤保新，陈 健，路培国 （扬州大学土木工程系，江苏 扬州225127）

对连续型随机变量 （或向量）函数的概率密度，其常规求解方法［1－2］是分布函数法。当随机变量函数有反函数或分区域有反函数且反函数可导时，其概率密度可直接求得。一般情形时，其概率密度有积分形式 （理论解），但该理论解含有广义函数，仅对少数类型的函数可运用变量代换的技巧得出积分的解析解，而对大多数类型的一般函数不便直接求解析解。间接的方法是概率密度演化方法［2］，通过引入时间变量，先将问题转化为关于联合概率密度的偏微分方程，进而求得边缘密度；但该偏微分方程的初始条件亦含有广义函数，不便于求解析解。为此，笔者通过引入辅助随机变量，提出了一种求解连续随机变量函数概率分布的新方法，为一般类型随机函数概率分布的数值计算提供了理论依据。

1 常规解法

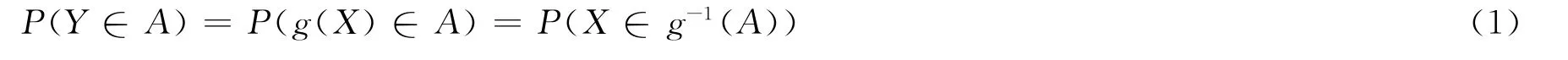
式 （1）是计算随机函数概率分布的基本公式。

对连续型随机变量X，设其概率密度为fX（x），当Y＝g（X）为严格单调且反函数可导时，可利用反函数求得：

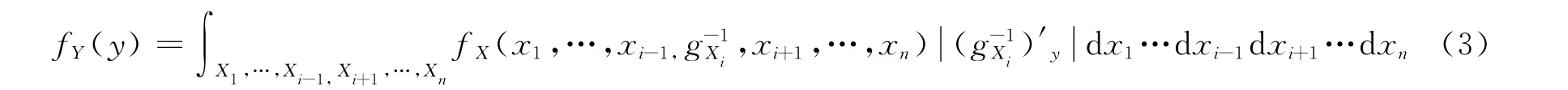
再求Yi＝gi（X）的边缘密度：

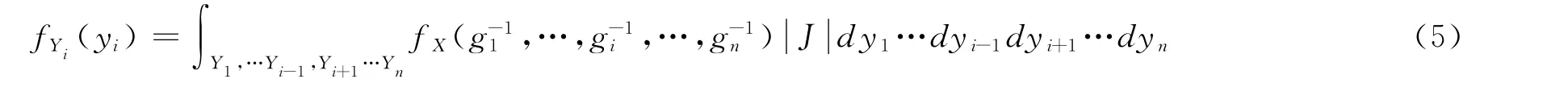
上述公式的关键条件是Y＝g（X）有反函数存在。此条件可推广为：将X划分为m个互不相交的区域在每个区域上反函数存在，亦可求得Y的联合密度：

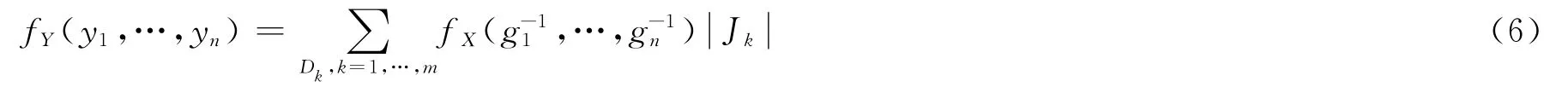
进而求得边缘密度。

常规解法的要求较苛刻，一是要求反函数存在或分区域反函数存在，在实际工程中一般难以满足；二是需要求导，增加了计算难度。

2 辅助随机变量解法

研究随机函数：

的概率分布。式 （7）中，X的概率密度为fX（x）；E为引入的已知辅助随机变量，其概率密度为fE（ε），X与E相互独立；Y＝g（X）的概率密度fY（y）待求。

显然，X 与E 有 联 合 密 度fX（x）fE（ε），Z对E 有反函 数E ＝Z－g（X），雅 可 比 行 列 式由式 （3）可求出Z的概率密度为：

另外，由于X与E相互独立，则Y＝g（X）与E相互独立，对式 （7）有卷积积分：

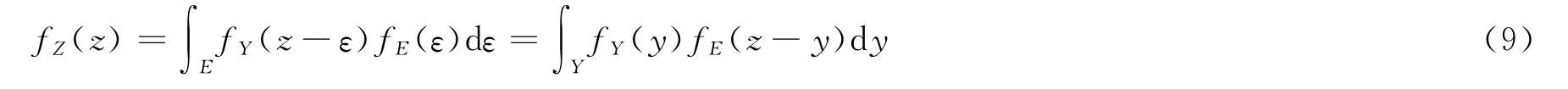
式 （8）仅对少数类型随机函数可通过反函数或换元法求得，一般情形下需采用数值积分。式 （9）为第一类Fredholm积分方程。由式 （8）求得fZ（z）后，再由式 （9）求得fY（y）。

特别地，当E＝0时，其概率密度为单位脉冲函数 （亦称Dirac函数）：

则Z＝Y，式 （8）变为：

式 （10）含有广义函数δ（ε），仅对少数类型函数可利用广义函数的积分性质求得。

3 傅里叶变换解积分方程

求解积分方程常采用积分变换方法。

对式 （9）进行傅里叶变换：

求出Y的傅里叶变换：

式 （11）进行傅里叶逆变换，即得Y的概率密度：

对式 （10）进行傅里叶变换，求出Y的傅里叶变换：

式 （14）进行傅里叶逆变换，即得Y的概率密度，同式 （13）。

4 算 例

辅助随机变量E可取常用概率分布，其定义域为整个实数域。当采用积分变换求解时，辅助随机变量应便于求傅里叶变换；当采用换元法求解时，辅助随机变量应与待求函数匹配。如取正态分布，其傅里叶变换为或指数分布，其中为单位阶跃函数 （亦称示性函数），其傅里叶变换为

例1 已知X～N（0，1），求Y＝X2的概率密度。

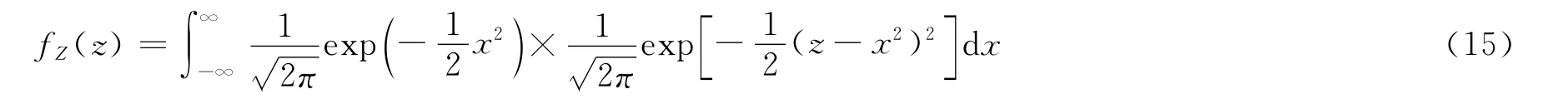
式 （15）指数最高为4次，难以直接积分，可先对z进行傅里叶变换，将指数降为2次，再积分：

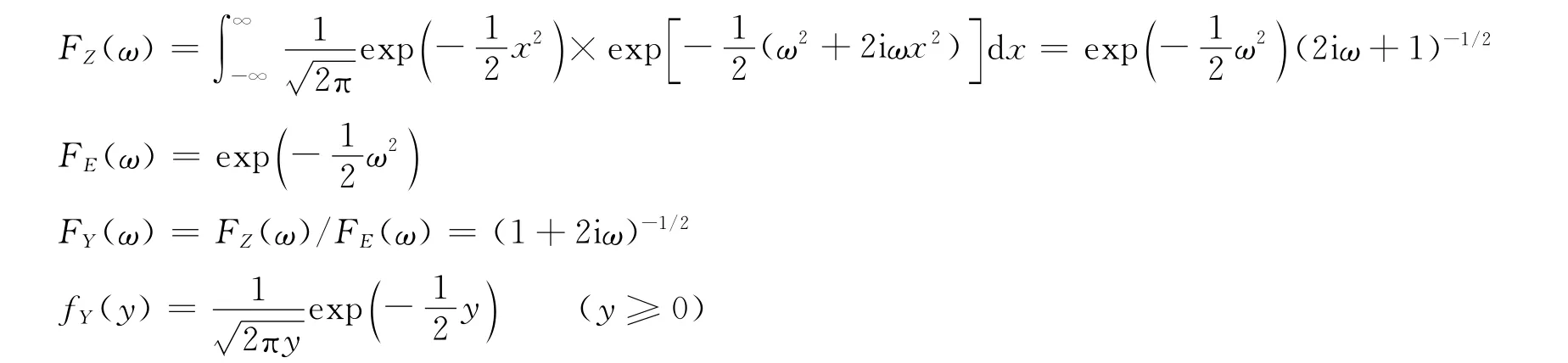
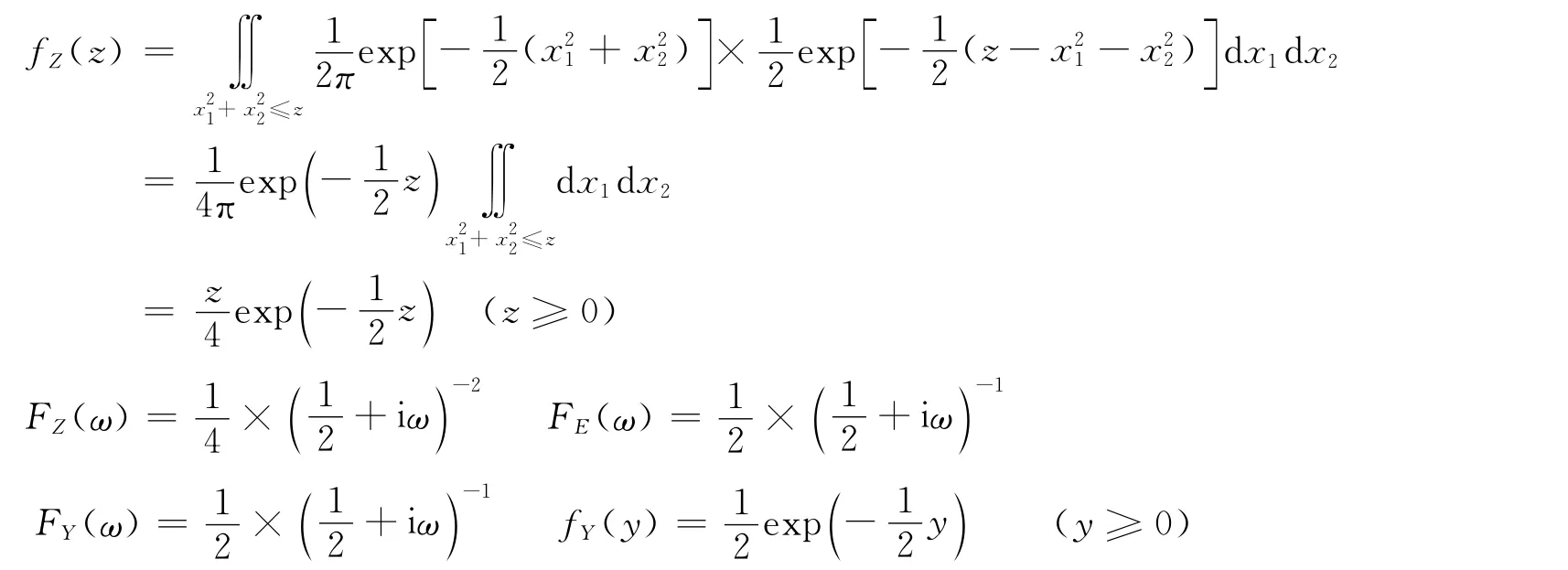
以上算例分析表明，该解法对少数类型随机函数可求得解析解，这为一般类型随机函数概率分布的数值计算提供了理论依据。

［1］李思齐，李昌兴，柳晓燕 ．二维连续型随机变量函数的分布密度的计算 ［J］．大学数学，2011，27（5）：162－166．

［2］《现代应用数学手册》编委会 ．概率统计与随机过程卷 ［M］．北京：清华大学出版社，2000：42－46．

［3］李杰，陈建兵 ．随机动力系统中的广义密度演化方法 ［J］ ．自然科学进展，2006，16（6）：712－719．