BD-2/GPS组合导航系统选星算法及定位分析

应士君， 李金金， 刘卫， 邱烺

(上海海事大学 商船学院，上海 201306)

0 引 言

随着卫星导航系统在各个领域中的应用，人们对卫星定位技术的要求越来越高，而定位精度是判断卫星定位效果好坏的最主要标准.[1]目前，世界上投入实际运行的全球定位系统只有美国的GPS和俄罗斯的GLONASS，还有正在建设中的中国北斗二代(BD-2)卫星导航定位系统和欧洲的伽利略系统.北斗卫星导航系统(BeiDou(COMPASS)Navigation Satellite System)是我国正在实施的自主发展、独立运行的全球卫星导航系统，是具有民族意义的研发项目.2012年9月19日，第14和15颗北斗导航卫星被成功送入预定转移轨道.

多系统组合定位[2]具有可见卫星数(Visible Satellite Number,VSN)多、定位精度高等优点，所以多系统组合的研究显得尤为重要.由于多系统组合增加VSN，如何快速、准确地选择定位卫星在整个导航定位过程中起着至关重要的作用，本文主要介绍BD-2/GPS组合导航系统[3]的选星算法.目前的选星算法主要有传统选星算法、基于卫星几何精度因子(GDOP)贡献法[4]、基于仰角和方位角法[5]及模糊选星算法等，BD-2/GPS组合导航系统VSN增加，传统的选星算法计算量大，不能达到快速定位[6]的要求.本文提出一种基于遗传算法的定位选星算法，将各组卫星中最优GDOP作为算法寻优的目标函数，选出最佳定位卫星组合，最后通过48 h实地观测数据对比分析最佳GDOP算法和本文所提选星算法的定位精度，最终验证该算法的可行性及优越性.

1 组合系统GDOP算法改进

卫星导航在一定的伪距测量误差下，一般利用GDOP表征定位精度的大小，反映由于卫星几何布局的影响所造成的伪距测量误差与定位误差间的比例系数，是对伪距测量误差的放大倍数.定位卫星选择的基本原则就是选取GDOP最小的卫星组合，使可选卫星组合的定位精度达到最大.[7]由于利用BD-2/GPS组合系统定位增加钟差变量，所以至少需要5颗卫星实现定位、定时计算.GDOP(式中用λGDOP代替)计算过程如下：

(2)

式中:l,m,n表示方向余弦;N表示用于解算的卫星个数.观测矩阵为

(3)

则几何误差系数可以表示为

(4)

式中:t代表矩阵求迹运算.从式(4)可见，每计算一次λGDOP就要进行一次矩阵乘和矩阵逆运算，组合系统VSN的增加使运算量加大，系统实时性较差.因此，可化简式(4)，避免矩阵乘和矩阵逆运算[8].

简化式(4)可得：

(5)

经化简，λGDOP可表示为

(6)

式中:aij表示观测矩阵的伴随矩阵元[9].

2 BD-2/GPS组合导航系统的选星算法

选星在导航定位中起着至关重要的作用，选择最佳几何构成的星座可以达到高精度的定位要求，因此需要合适的选星算法完成快速、准确的星座组合[10].遗传算法模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象，在每次迭代中都保留一组候选解，并按某种指标从解群中选取较优的个体，利用遗传算子(选择、交叉和变异)对这些个体进行组合，产生新一代的候选解群，重复此过程，直到满足某种收敛指标为止.[11]基于遗传算法比传统优化算法应用范围广、全局优化性好、鲁棒性和通用性强、隐含并行性高、易于实现等优势，本文提出一种基于遗传算法的选星算法[12].

同时，由于GDOP是影响卫星定位精度的主要因素之一，GDOP的大小代表定位精度的高低，GDOP越小，定位精度越高，故以GDOP计算模型作为遗传算法中判断解优劣的适应度函数.

由卫星对地面目标和地球的覆盖特性可知，顶座星仰角越大GDOP越小，底座星仰角越小GDOP越小，所以最佳星座组合中必然包括仰角最大和最小的那两颗卫星.将GPS导航卫星从0到23分别编号，北斗导航卫星从24到38分别编号.BD-2/GPS组合导航系统在高度角大于5°时，平均捕获跟踪12颗卫星，从中选择仰角最大的卫星(假设为6号卫星，则字符串编码为000110)；25号卫星编码为011001，然后从剩下的11颗卫星中任意选取4颗卫星进行组合.假设选取的样本为1号、15号、23号、30号、32号卫星，则染色体编码为000001 001111 010111 011110 100000.经过交叉变异，适应度较高的部分样本遗传到下一代，再进行交叉变异，最终达到最优解，选择最佳几何构成的星座组合.选星算法流程见图1.

图1 选星算法流程

以上工作全部由软件完成，通过软件计算最终得到GDOP最小的组合卫星编号.

3 BD-2/GPS组合导航系统实验结果分析

导航接收天线安装在上海海事大学商船学院C楼楼顶，位置为：30°52′26.927″N，121°54′7.974″E.接收机参数设置如下.

定位参数设置：信噪比门限值为36 dB/Hz，高度角为5°，PDOP(空间位置精度因子)门限值为36，RAIM(接收机自主完好性监控)门限值为80.

接收机基带工作参数设置：多普勒频率搜索区间为-10～10，500 Hz，环路积累时间为4 ms，环路类型为3PLL，锁相环带宽为18 Hz，锁频环带宽为5 Hz.数据分析结果如下.

3.1 VSN

图2，3和表1为48 h内接收机同时工作在两种不同定位模式下的VSN示意图.

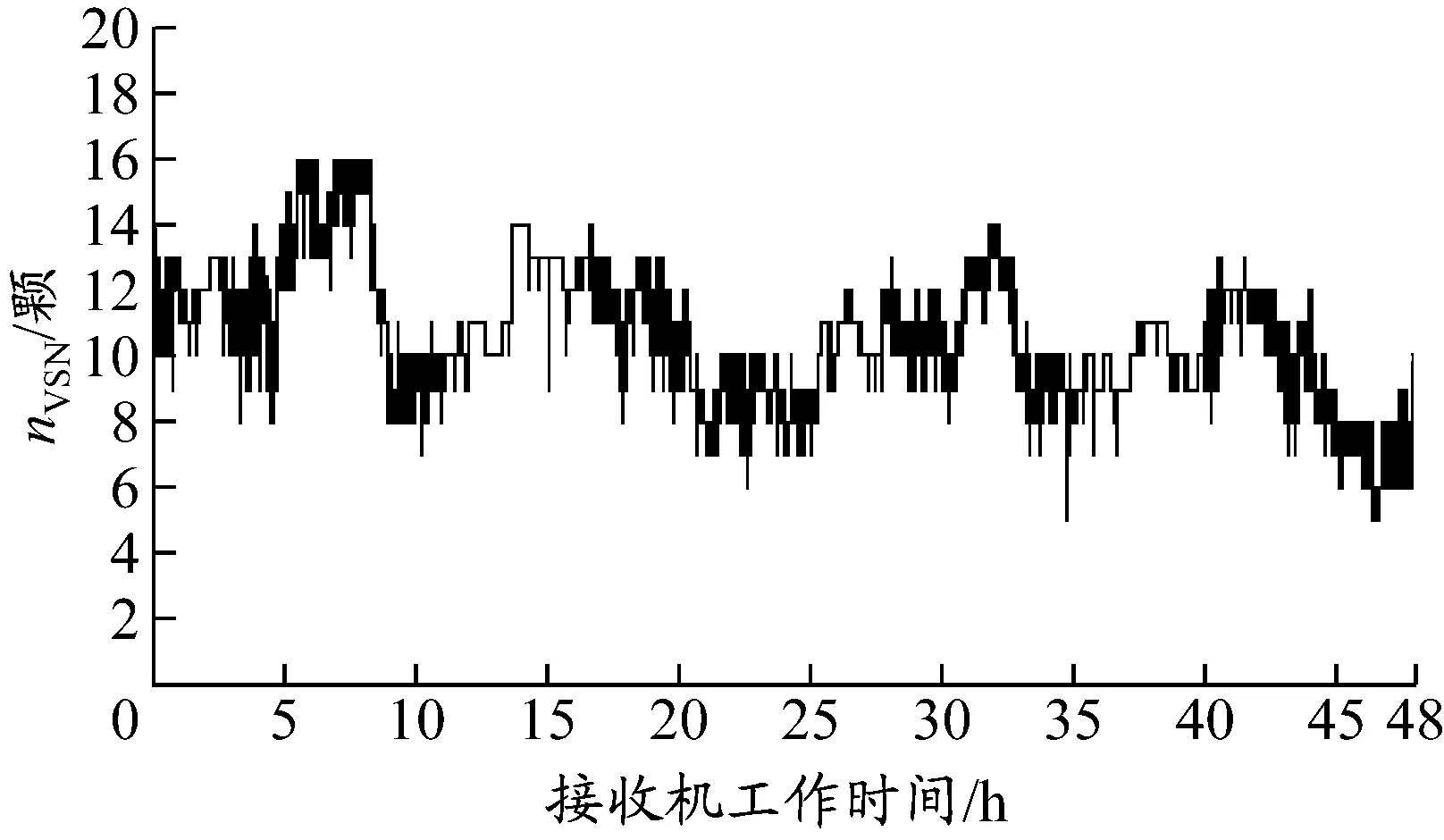
图2 BD-2/GPS导航系统VSN

通过以上数据可以明显看出，组合导航系统在相同条件下能够捕获的卫星数目远大于单一系统.

图3 GPS导航系统VSN

表1各系统VSN颗

导航系统最多最少平均BD⁃2/GPS16512GPS1348

组合导航系统可以选择最合适的星座组合，达到高精度定位要求，特别是在恶劣环境下，也可以有足够数目的卫星进行星座组合，达到定位要求.

3.2 某一采样时段内可见卫星的原始数据

此时段内捕获跟踪到16颗卫星，GPS导航卫星9颗，北斗导航卫星7颗，卫星分布均匀，为选择最佳星座组合提供足够的卫星.可见卫星的原始数据见表2.

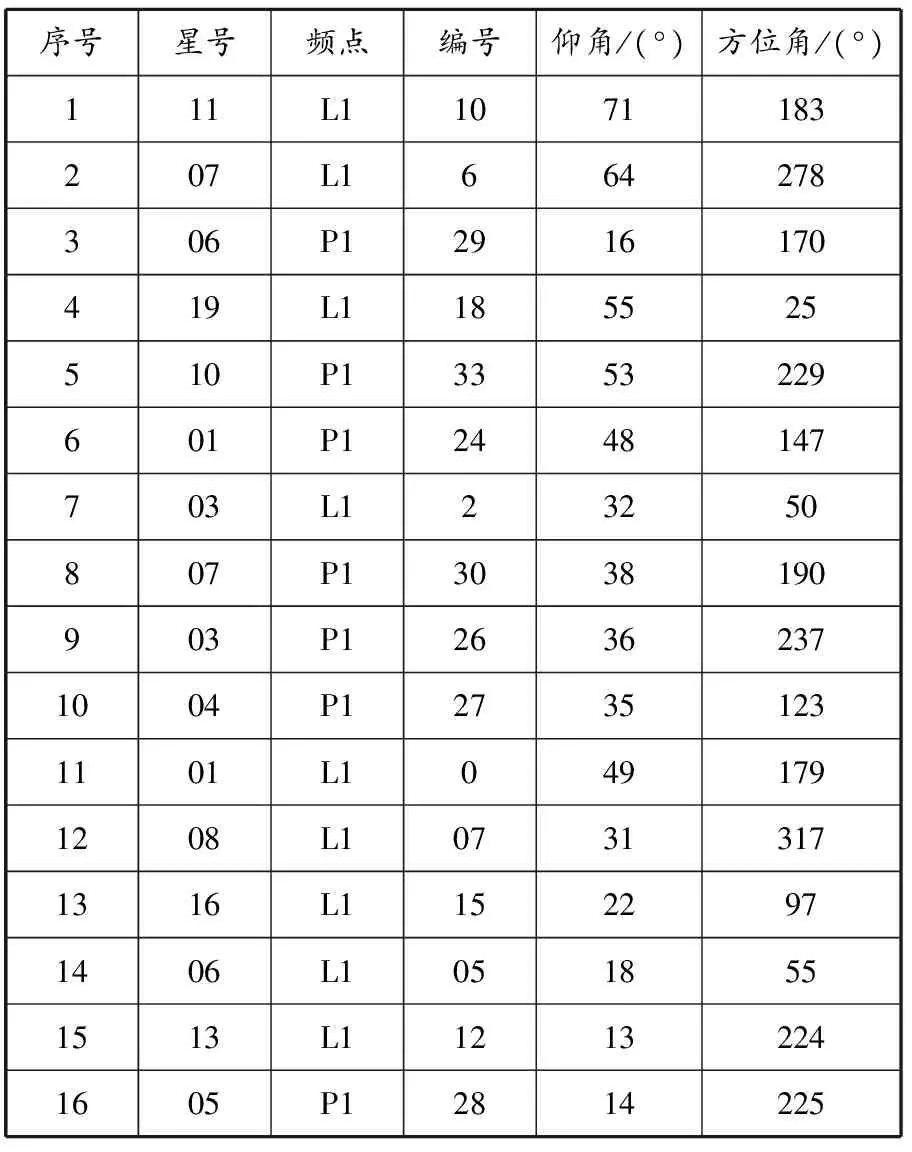
表2 可见卫星的原始数据

通过表2可以看出:仰角最大的卫星是GPS的11号星，本文设置编号为10;仰角最小的卫星是GPS的13号星，本文设置编号为12.所以，最佳卫星星座组合必然包括GPS的11和13号星.

矩阵乘法和矩阵求逆运算比较复杂，在计算机上实现占用资源相当多[13]；而利用本文提出的方法，首先将GDOP计算过程简化，避免大量矩阵运算，然后通过仰角选出2颗定位卫星，最后通过遗传算法选择最终定位卫星组成.某一采样时段内最佳GDOP算法与本文提出算法的分析结果见表3.

表3 某一采样时段内的分析结果

48 h内最佳GDOP算法与本文提出选星算法的λGDOP及差值对比见图4～6.

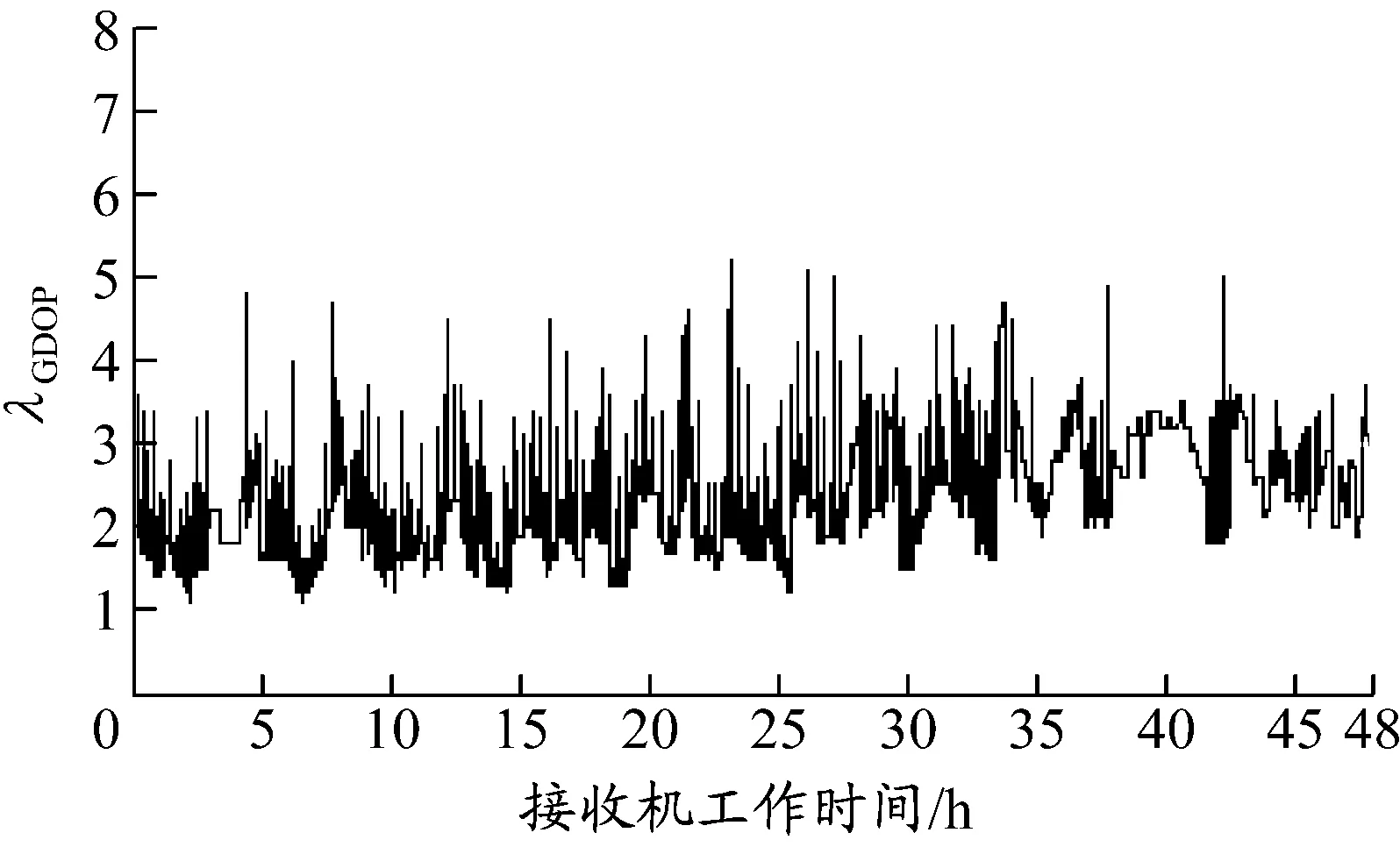
图4 本文提出选星算法的λGDOP

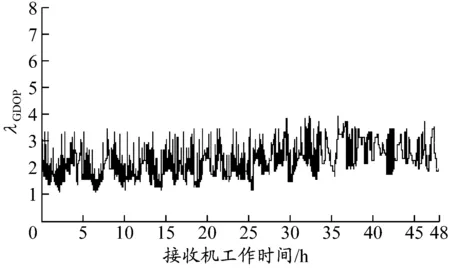
图5 最佳GDOP算法的λGDOP

图6 本文提出选星算法与最佳GDOP算法的λGDOP差值变化曲线

通过表3和图4～6可见：本文提出选星算法得出的λGDOP和最佳GDOP法得到的λGDOP的误差值很小，48 h内输出172 696个数据的λGDOP差值平均为0.063 042 945，最大误差为3.1，最小误差为0.在部分时间段内出现较大差值，是由于遗传算法寻优过程出现局部最优解.在遗传算法中，交叉和变异算子发生的频率分别由交叉概率和变异概率控制；在迭代过程中，由于随机误差使得全局最优解有可能丢失，所以需要设置适当的交叉概率值和变异概率值.对于出现局部最优情况，可以通过以下几种方法解决：根据个体适应度值，自适应地调节交叉概率和变异概率；群体有陷入局部最优解的趋势时，相应提高交叉概率和变异概率；群体在解空间发散时，降低交叉概率和变异概率；也可以使用模拟退火算法或神经网络[14]方法进行改进.

数据设置每秒更新1次，最佳GDOP算法与本文提出算法在20 min内所用时间对比见图7和8.

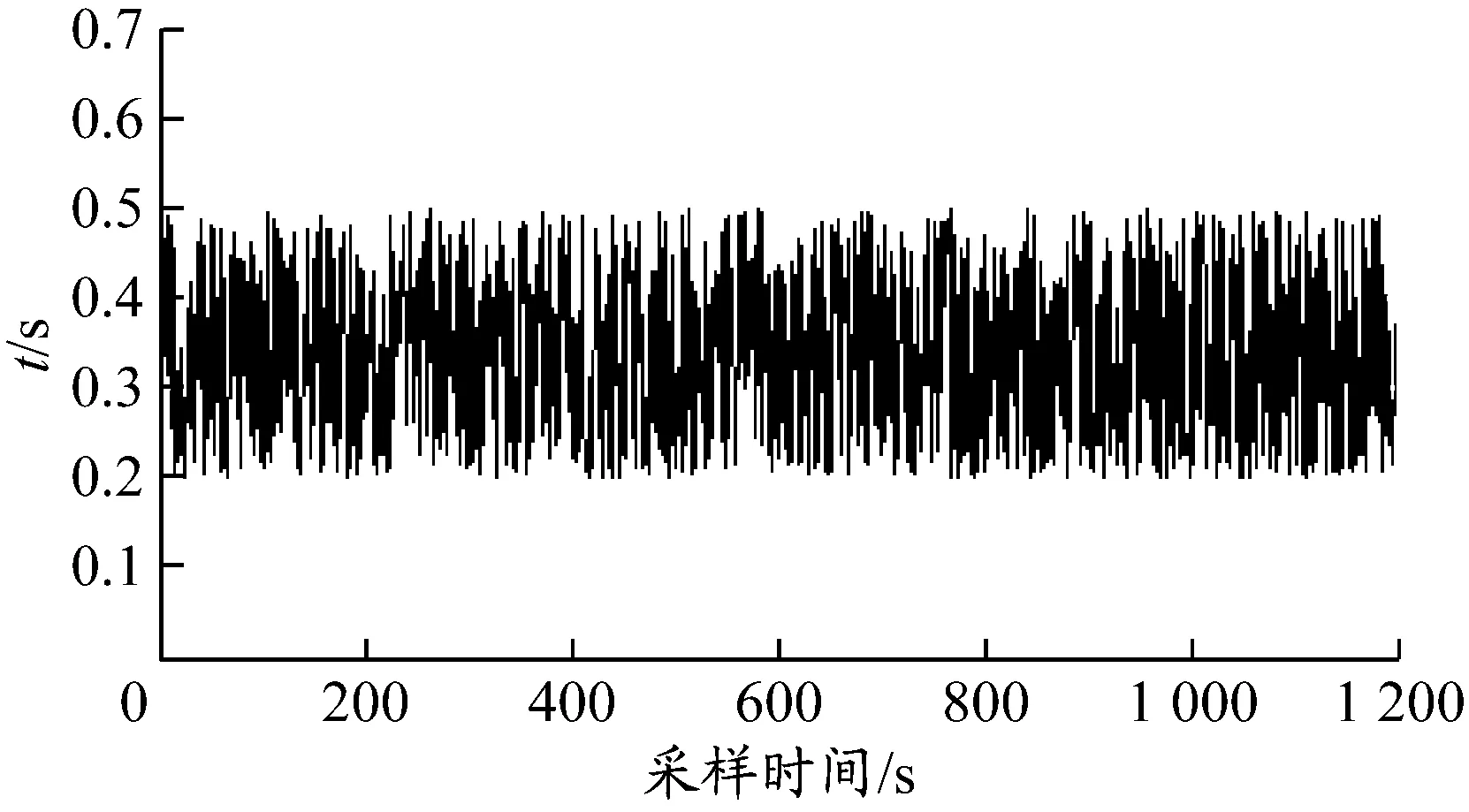
图7 最佳GDOP算法所用时间变化曲线

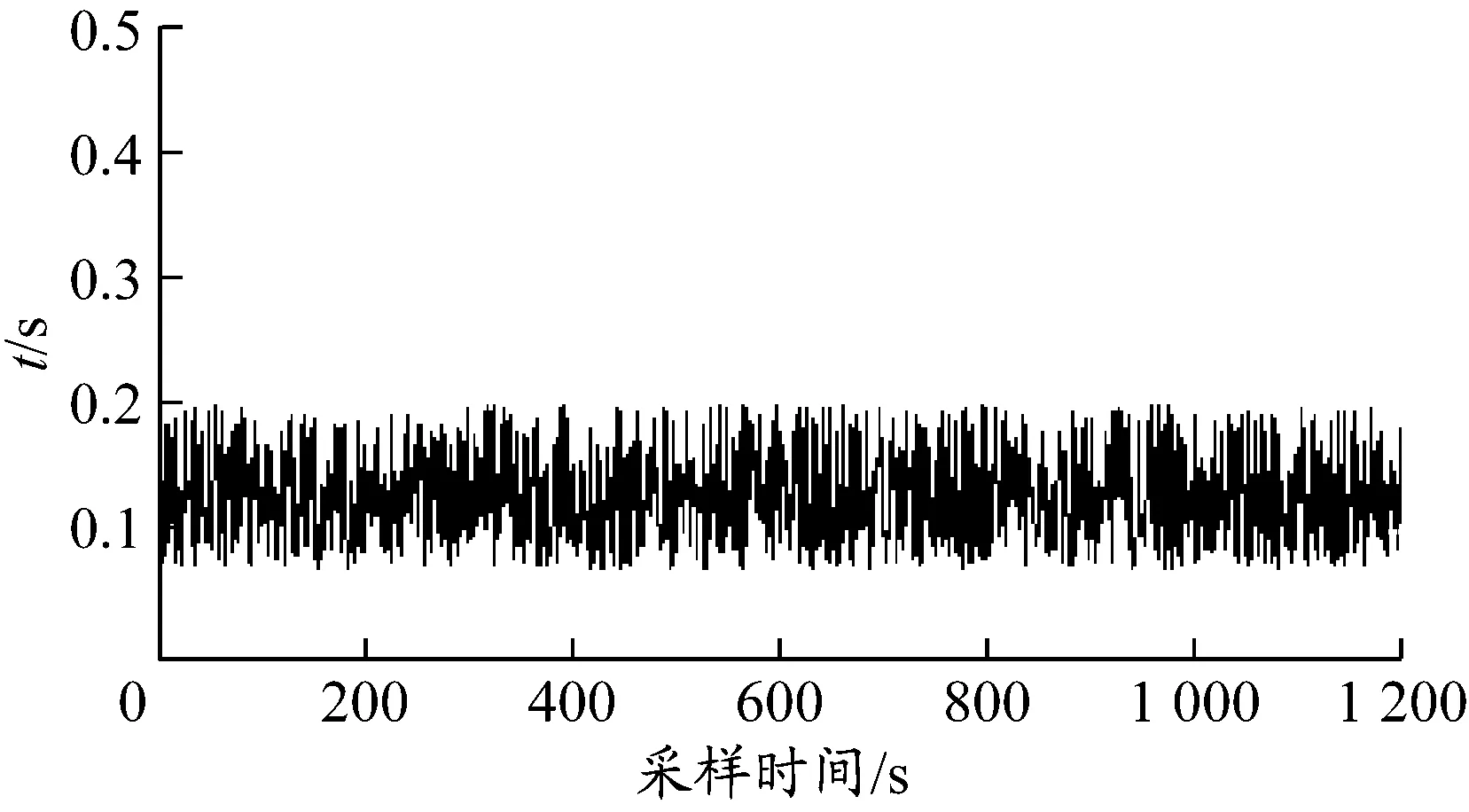
图8 本文提出算法所用时间变化曲线

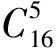
4 结束语

将可见卫星仰角与遗传算法相结合，以GDOP计算模型作为遗传算法中判断解优劣的适应度函数，提出一种新的组合导航系统选星算法.算法同时将GDOP计算过程简化，结合遗传算法寻优的特点实现最优定位卫星组合的快速求解，在达到定位精

度要求的前提下有效节省算法的执行时间，效率大大提高.实验数据分析结果验证算法的可行性、准确性和快速性.

参考文献：

[1] 孙洪瑞, 沈云中, 周泽波. GPS/GLONASS组合点定位模型及其精度分析[J]. 测绘工程, 2009, 18(1): 8-10.

[2] 庞春雷, 赵修斌, 卢艳娥, 等. BD-2/GPS双模导航定位精度分析及仿真[J]. 现代防御技术, 2011, 39(4): 35-54.

[3] 孙延鹏, 张赢硕, 王尔申, 等. BD-2/GPS组合系统的设计与定位算法[J]. 电子设计工程, 2011, 19(23): 74-77.

[4] 丛丽, 谈展中. 提高卫星导航定位精度和实时性的选星算法[J]. 系统工程与电子技术, 2008， 30(10): 1914-1917.

[5] 吴瑞祥, 蔡体菁. 基于高度角和方位角的选星方法[J]. 舰船电子工程, 2009, 185(11): 73-75.

[6] 高迪驹. 基于北斗卫星通信系统的船载终端串口通信[J]. 上海海事大学学报, 2008, 29(4): 10-14.

[7] HURSKAINEN H. Research tools and architectural considerations for future GNSS receivers[D]. Tampere, Finland: Tarnpere Univ of Technol, 2009.

[8] MA Rui, MA Yingli. Study on positioning algorithm for the combined Galileo/GPS system[J]. J Telemetry Tracking & Command, 2009, 30(1): 7-11.

[9] 黄继拯, 刘红, 赵艳, 等. GPS/北斗的组合选星算法研究[J]. 舰船电子工程, 2011, 32(8): 81-83.

[10] 金玲, 黄智刚, 李锐, 等. 多卫星组合系统的快速选星算法研究[J]. 电子学报, 2009, 37(9): 1931-1936.

[11] 白治江, 刘广钟. 递归式多目标遗传算法[J]. 上海海事大学学报, 2007, 28(2): 62-74.

[12] 张尚悦, 贾传荧. 基于遗传算法的最佳天文定位星座组合[J]. 交通运输工程学报, 2004, 4(1): 110-113.

[13] 应士君, 王坤, 刘卫, 等. 基于北斗二代系统的船载定位终端[J]. 上海海事大学学报, 2012, 33(3): 1-4.

[14] 朱武亭, 刘以建. BP网络应用中的问题及其解决[J]. 上海海事大学学报, 2005, 26(2): 64-66.