基于免疫遗传算法的线状要素图形简化方法研究
马潇雅,郭庆胜,2
(1.武汉大学资源与环境科学学院,湖北武汉 430079;2.武汉大学测绘遥感信息工程国家重点实验室,湖北武汉 430079)
一、引 言
作为占地图图形80%以上的地图目标,线状要素的自动综合自然成为地图综合的一个重要方面。图形简化作为其综合的重要手段之一,已得到国内外有关学者的持续关注,并研究实现了大量自动化算法[1-4],如著名的道格拉斯算法、Li-Openshaw算法等。随着智能优化算法的广泛应用,有关学者在线状要素图形简化的智能优化算法探索中也已取得一定成效,提出了基于遗传算法[5]和蚁群优化算法[6]的线状要素图形简化模型,并证明了智能优化算法是解决线状要素图形简化问题的一个有效途径。
免疫遗传算法是人工免疫系统模型的重要组成部分,该算法将免疫系统生理学机制和自然生物进化机制相结合,具有强大的空间搜索能力[7-8],在优化问题的解决上具有很大优势。本文在现有线状要素图形简化的研究基础上,提出一种基于免疫遗传算法的线状要素图形自动简化方法。并将试验结果与单纯免疫算法、遗传算法和道格拉斯算法进行对比,试验表明基于免疫遗传算法的线状要素图形简化方法在保持线状要素图形形状方面表现更佳。
二、基于免疫遗传算法的线状要素图形简化方法
基于免疫遗传算法的线状要素图形简化的本质是将线状要素图形简化问题转化为抗原,线状要素图形简化方案转化为抗体,抗原和抗体间的亲和力值则是衡量抗体与抗原的亲和度,图形简化即为寻找与抗原亲和度最高的抗体的过程。为达到保证数据质量和可视化要求的同时,尽可能减少曲线上的点数,并保留关键点(包括曲线的端点、极值点、拐点等)的图形简化目标[9],本文依据免疫遗传算法的基本原理,顾及线状要素的几何精度和形状特征点保留的约束条件,引入不可行解的修复机制,提出线状要素图形简化方法。
1.编 码
编码的本质是将线状要素图形简化方案转换成免疫系统中的抗体,并且每个抗体对应一种图形简化方案。本文采用二进制编码构造算法的抗体,编码的长度为线状要素上节点的数目,每个基因位储存该节点的状态,0为舍弃,1为保留。同时,线状要素的首尾两个节点为必须保留点。
2.亲和度函数设计
在采用免疫遗传算法进行问题求解时,通常抗体的亲和度高低反映了抗体(问题的解)满足抗原(问题)的程度,即抗体的亲和度值越大,抗体(问题对应的解)越优。在对线状要素图形简化结果进行评价时,亲和度函数的设计仅考虑保留点个数及特征点保留两个约束条件,几何精度的保证则通过引入不可行解的修复机制解决。
本文把对线状要素图形形状的保持起重要作用的节点认为是线状要素的形状特征点,各节点的重要程度,由其贡献值体现。根据文献[10]的方法,各节点的贡献值可通过该节点两相邻的直线段长度L(S1)、L(S2)及两线段的转角β(S1,S2)综合计算得到[10],计算公式如下

基于免疫遗传算法是一个寻求保留节点的贡献值最大、图形表示节点个数最少,以及图形简化后在距离限差内应舍弃的保留节点个数最少的抗体的过程。该算法中抗体亲和度值可通过式(2)计算得到

式中,Ki为线状要素第i个保留节点的贡献值;Nr为保留节点的个数;Nd为图形简化后距离限差内应舍弃的保留节点个数。其中,Nd的探测方法为:解码抗体,沿线状要素的数字化方向依次遍历并计算各保留节点与其相邻两保留节点连线的垂直距离,且判断该距离是否小于指定限差,是则说明该节点应被舍弃。
3.算法流程及主要算子设计
基于免疫遗传算法线状要素图形简化方法的流程如下:
1)随机产生初始抗体种群Ab(0),令当前算法迭代次数为T=0。
2)对抗体种群Ab(k)执行克隆操作,得到新抗体种群Abc(k)。
3)对抗体种群Abc(k)执行高频变异操作,得到新抗体种群Ab'c(k)。
4)对抗体种群Ab'c(k)执行交叉操作,得到新抗体种群Ab*(k)。
5)对抗体种群Ab*(k)中的抗体执行修复操作,得到新抗体种群Ab'*(k)。
6)根据式(2)计算所有抗体的亲和度。
7)对抗体种群Ab(k)和Ab'*(k)执行克隆选择操作,得到新抗体种群Ab(k+1)。
8)令T=T+1,若满足终止条件,算法停止,将抗体种群中最优的抗体解码为线状要素图形简化方案;否则,返回步骤2)。
该算法中主要算子操作如下:
(1)克隆操作
克隆倍数决定算法的局部搜索能力及计算量。为获得较好的图形简化效果,简化方案对应抗体的亲和度越高则抗体被复制的倍数应越大。其中,抗体被克隆的倍数可通过式(3)计算得到[7]

式中,Nc为抗体被克隆的倍数;β为增值系数,由用户预设;N为种群规模;round()为取整数操作。如N=10,β=1,则亲和力最高的抗体(i=1)将被克隆10倍,亲和度次高的抗体将被克隆5倍。
(2)高频变异
变异是免疫遗传算法中抗体亲和度成熟和抗体多样性产生的主要手段,决定着算法的全局搜索能力,变异概率决定算法收敛性能。本算法中抗体的变异是将抗体上某个基因位的值取反的过程,如图1所示。在进行变异操作时,各抗体上的基因值均按照一定的概率Pm随机确定该基因位是否进行变异。

图1 抗体变异原理
(3)交叉操作
交叉是免疫遗传算法保持种群进化过程中抗体多样性的辅助方式,决定算法的局部搜索能力。常用的交叉方式有单点交叉、两点交叉和均匀交叉。本算法采用单点交叉方式,即将2个被选中抗体的基因链按照一定概率Pc进行交叉,生成2个新的子抗体,交叉位置是随机的(如图2所示)。

图2 抗体交叉原理
(4)不可行解的修复
不可行解修复机制的引入是为了保证线状要素图形简化过程中的几何精度,其本质是将抗体解码为线状要素图形简化方案,以判断线状要素上各节点的保留及舍弃是否合理。具体操作步骤如下[6]:
1)判断节点的舍弃是否合理。沿线状要素方向依次取2个相邻的保留节点,若该两节点间存在已被舍弃的点,则寻找出与此两节点连线距离最远的节点,计算该距离。若该距离小于指定的距离限差,则说明此两节点间其他节点的舍弃均合理。继续搜索判断节点舍弃的合理性,若搜索至最后一个节点则转到步骤2),否则继续转到步骤1)执行;若该距离大于指定距离限差,说明搜索到的节点为不应舍弃的点,将该点的抗体基因位的值由0变成1,继续转到步骤1)执行。
2)判断线状要素上各保留节点的选取是否恰当。沿线的方向依次取3个相邻保留节点,计算中间节点到前后两相邻保留节点连线的垂直距离。若该距离小于指定距离限差,则说明该节点是应舍弃的点,将其抗体上该节点基因位上的值由1变为0,继续转到步骤1)执行;若该距离大于指定距离限差,说明该节点的保留是恰当的。
三、试验与分析
1.试验数据
本文采用的试验数据为某县级境界线的部分数据,原始线状要素如图3所示,线上有726个节点。本文将用不同的算法以不同的距离限差作为线状要素数据压缩的条件进行试验。

图3 原始线状要素
2.试验结果分析
试验采用的距离精度限差为1~3 m。当距离为1 m时,设置免疫遗传算法的种群规模为100,增值系数为0.08,变异率为0.01,交叉率为0.002,运行代数为200代。图4是距离限差为1 m时免疫遗传算法、免疫算法、遗传算法和道格拉斯算法4种算法简化后的图形;图5是算法收敛曲线。各算法在不同距离限差条件下简化结果指标值见表1。

图4 距离限差为1 m的图形简化结果
由试验结果可得到以下结论:
1)图形上。4种算法的简化结果均能较好地保持线状要素的形状。道格拉斯算法在保持极值点方面表现较好;智能优化算法在保持对线状要素形状保持贡献更大的点方面表现更佳,简化后的图形效果更好;免疫遗传算法和单纯免疫算法的简化结果一致,优于遗传算法的简化结果。
2)优化算法效率。从算法收敛图看,当距离限差为1时,免疫遗传算法在运行118代后找到最优解;免疫算法运行185代后解达到最优;遗传算运行200代仍未找到最优解。免疫遗传算法的收敛速度明显快于单纯的免疫算法和遗传算法,算法效率更高。
3)综合指标。从表1可看出,免疫遗传算法相对其他3种算法,在表示节点数相近的情况下,总的节点贡献值最大,亲和度函数值最大,算法保留了对图形形状贡献较大的点。免疫遗传算法在平衡保持线状要素图形特征点、减少保留节点数量和几何精度控制上表现更佳。
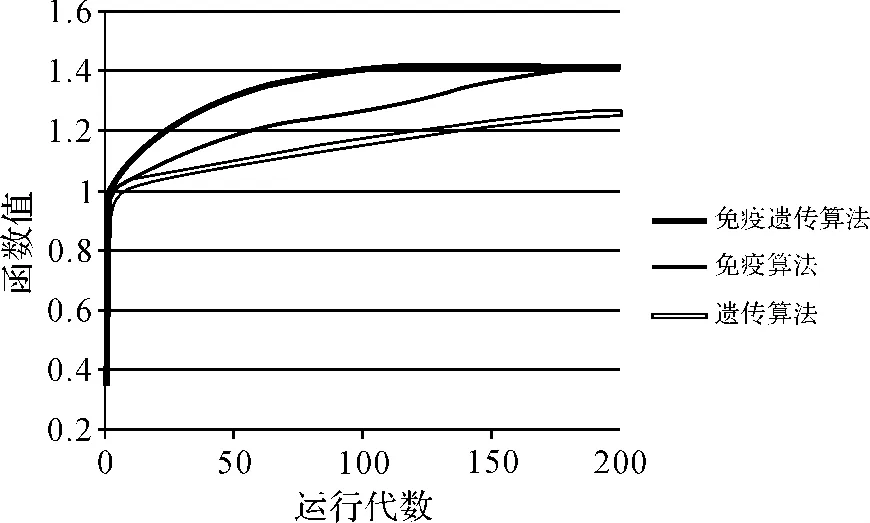
图5 算法收敛曲线图
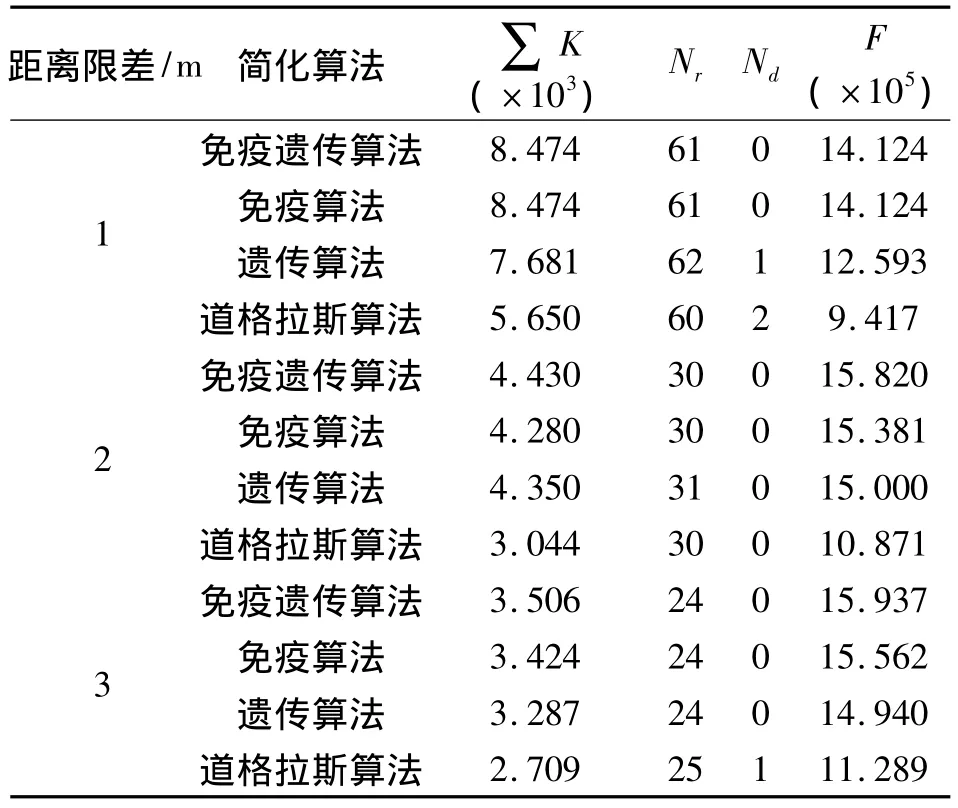
表1 不同距离限差下各算法的线状要素图形简化指标对比
四、结束语
本文顾及线状要素的几何精度和图形特征点,并结合不可行解修复机制,提出一种基于免疫遗传算法的线状要素图形简化方法,在线状要素图形形状特征的保持方面取得良好的效果,为智能算法应用于地图综合领域提供了一定的理论和实践基础。研究成果也能为地图生产提供相应的理论指导和技术支持。同时,线状要素简化过程中随着比例尺的缩小可能产生的空间冲突、地理信息语义不一等问题的处理仍有待作进一步研究。
[1] DOUGLAS D,PEUCKER T.Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J].The Canadian Cartographer,1973,10(2):112-122.
[2] LI Z L,OPENSHAW S.Algorithms for Antomated Line Generalization Based on a Natural Principle of Objective Generation[J].INT.J.Geographical Information Systems,1992,6(5):373-389.
[3] CROMLEY R G,GAMPBELL G M.Integrating Quantitative and Qualitative Aspects of Digital Line Simplification[J].The Cartographic Journal,1992,29(1):25-30.
[4] 郭庆胜.线状要素图形综合的渐进方法研究[J].武汉大学学报:信息科学版,1998,23(1):54-58.
[5] 武芳,邓红艳.基于遗传算法的线要素自动化简模型[J].测绘学报,2003,32(4):349-355.
[6] 郑春燕,郭庆胜,胡华科.基于蚁群优化算法的线状目标简化模型[J].测绘学报,2011,40(5):635-638.
[7] 梁勤欧.人工免疫系统与GIS空间分析应用[M].武汉:武汉大学出版社,2011.
[8] DE CASTRO L N,VONZUBEN F J.Artificial Immune System:Part I——Basic Theory and Applications[M].Campinas,SP:State University of Campinas,1999.
[9] 郭庆胜,黄远林,郑春燕,等.空间推理与渐进式地图综合[M].武汉:武汉大学出版社,2007.
[10] FREKSA C,BRAUER W,HABEL C,et al.Spatial Cognition II:Integrating Abstract Theories,Empirical Studies,Formal Methods,and Practical Application[M].Berlin:Springer,2000.

