基于不同高度角的对流层延迟改正模型选择
王利杰,李思敏,蔡成林,李天松
(桂林电子科技大学信息与通信学院,广西桂林541004)
一、引 言
对流层位于大气的最底层,下接地面,上至平流层起点,约40 km的范围,集中了约75%的大气质量和90%以上的水汽质量。云、雾、雨、雪等众多天气现象都发生在对流层。对流层对频率在30 GHz以下的电磁波都是非色散介质,因此所导致的传播路径较小,可忽略不计。而它对于GPS信号所导致的传播路径增长的距离就称为对流层延迟,一般而言,在天顶方向(高度角为90°)对流层延迟约为2~3 m;当高度角小于10°时约可达15~20 m;而当高度角更小的时候,其延迟量将会更大[1-2]。
目前在对GPS数据进行处理时,很多学者都使用模型进行对流层延迟改正,但模型改正在面对实际数据处理的时候效果如何、具体差异在哪里,并没有过多的研究,只有很少一部分对根据各种模型计算出来的随高度角变化的对流层延迟量的具体数值及各种模型之间的差异进行了深入的研究。即使定量的分析之后,也并非某种延迟量越小越好;然而究竟该如何判断,本文给出了很好的解决方案。
目前在使用模型进行对流层延迟改正时,常见的比较有代表性的模型有Hopfield模型、Saastamoinen模型和Black模型。本文基于Matlab语言实现了这3种对流层改正模型,并利用IGS数据进行仿真分析,得出了比较合理的结论及算法。
二、3种常用对流层延迟改正模型的介绍
1.Hopfield改正模型
Hopfield模型是Hopfield于1969年[2]从全球性实测平均资料中总结出的,加以修正后的模型为
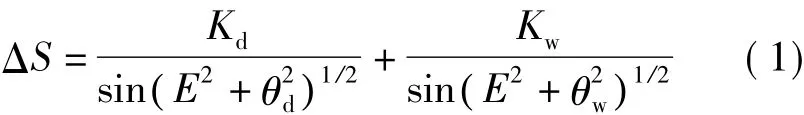
式中
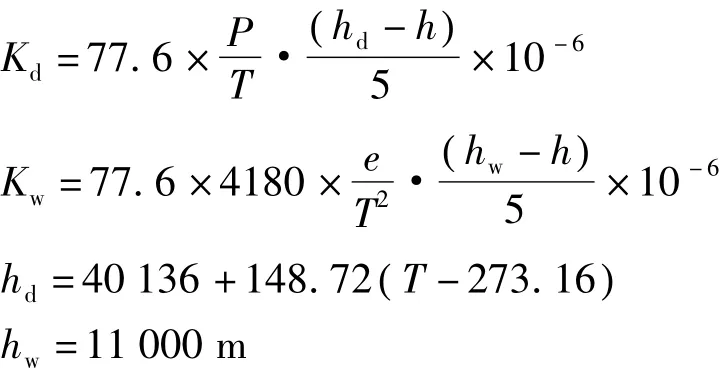
其中,ΔS为对流层延迟改正;Kd为天顶方向干分量延迟,Kw为天顶方向湿分量延迟,单位均为m;P为测站气压,e为测站水汽压,单位均为mbar;T为测站气温(绝对温度),单位为K;E为传播路径高度角,单位为(°);θd取为2.5°,θw取为1.5°;hd为干大气顶高,hw为湿大气顶高,h为测站高程,单位为m[3-5]。
2.Saastamoinen改正模型
Saastamoinen模型是Saastamoinen于1973年提出的,它是以测站纬度、高程、观测高度角、干温、水气压为变量的函数,其表达式为
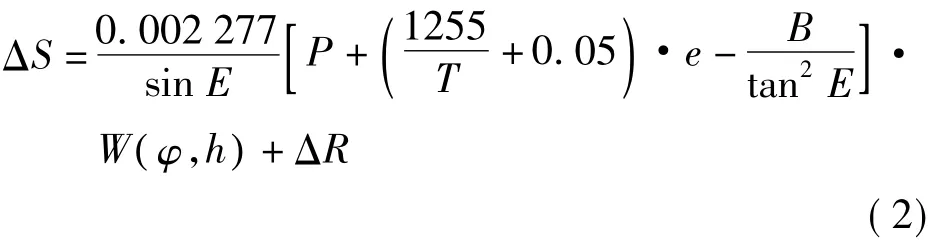
式中,W(φ,h)=1+0.002 6cos 2φ+0.002 8 h;h为测站高程;φ为测站所处纬度;B为h的列表函数;ΔR为E和h的列表函数[2]。
在实际应用中,由于式(2)不便于实时快速计算,所以在保证使用精度的前提下,对上式进行了拟合化简,拟合后的Saastamoinen模型为
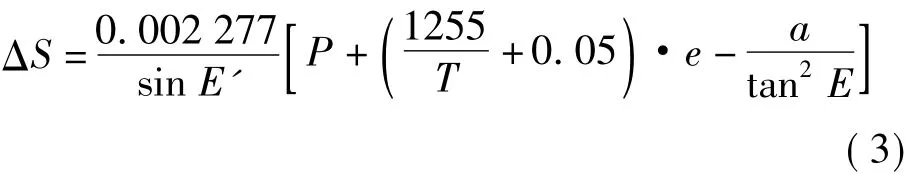
式中
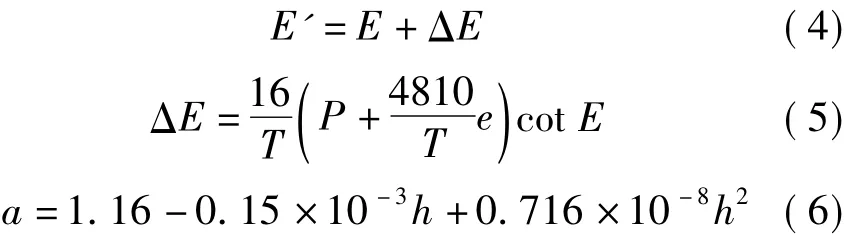
其他变量跟Hopfiled模型中的变量表示相同含义[6-7]。
3.Black改正模型
H.D.Black于1978年利用 Hopfield模型提出折射率表示方法,加上路径弯曲变量,给出了Black模型的表达式
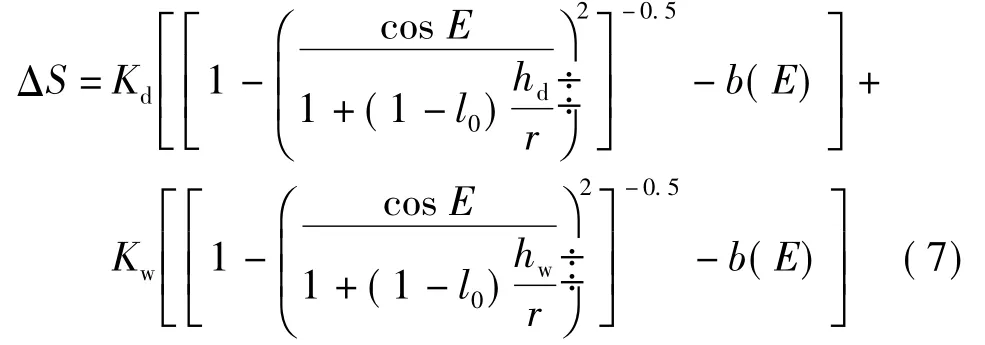
三、判断延迟量精确度的方法
伪距是由GPS观测而得到的GPS观测站到卫星的距离,而由于尚未对因“卫星时钟与接收机时钟同步误差”的影响加以改正,在所测距离中包含着时钟误差、电离层延迟误差、对流层延迟误差等因素在内,故称为“伪距”Pr,即
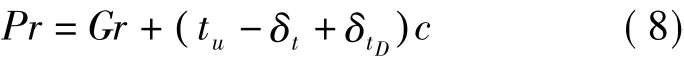
其中
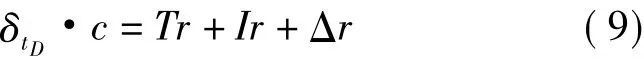
式(8)~式(9)中,Pr是伪距,Gr是几何距离,Tr是对流层延迟距离,Ir是电离层延迟距离,Δr是包含接收机噪声和干扰引起的误差、多径偏差及接收机的硬件偏差距离,单位均为m;tu是接收机钟差,δt是卫星钟差,δtD是除钟差外的时间偏差,单位为均s;c是光速,取值为299 792 458 m/s[9]。
式(8)中的伪距Pr、几何距离Gr及卫星钟差δt都在IGS数据里给出或可以直接计算出来,对于电离层延迟Ir可以通过“双频改正”的方法消除,在3种不同模型下又可以算出对流层Tr。因此,式中只差接收机钟差tu和误差Δr两项未知。接收机钟差tu的计算需要考虑到两颗或多颗卫星,而同一时刻不同卫星的高度角不同,不便于本文基于高度角选择模型进行分析,以及Δr中的变量考虑因素过于繁杂,而对本文的影响不是很大,故最终本文对此数据先不予考虑。因此由式(8)与式(9)可以看出,3种模型中如果哪种得出的结果更接近Pr,则说明那种模型改正更精确。
四、模型的实现与分析
1.模型实现
本文在Windows下使用Matlab语言实现了这3种对流层改正模型。而数据为北京测站关于G03卫星于2010年12月6日和7日两天的数据,其中分别作了两次实现。
(1)初步实现
由于考虑到测站的一些数据(如大气压、温度、水汽压)随时间变化不是很明显,所以首先假设在高度角变化的情况下,测站的大气压、温度、水汽压均为定值,以观察3种模型随着高度角变化而变化的问题。此时这些数据均取2010年12月6日0∶00的数值,高度角取3∶3∶90的变化。所得结果如图1所示。
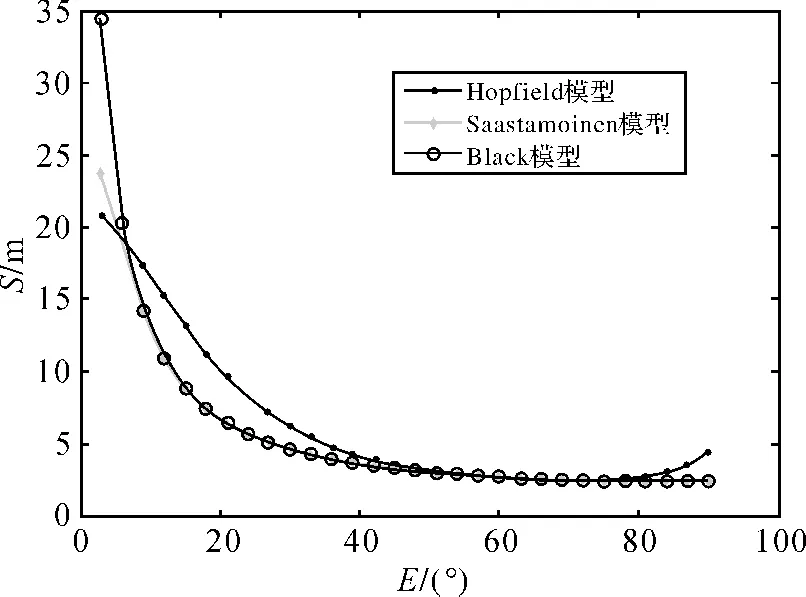
图1 在相同条件下不同高度角对3种模型的影响
由图1可以看出,3种模型的延迟量都是随着高度角的增加而大致减小的,只有Hopfield模型在高度角比较大的时候有一些“反弹”,这种现象与实际情况是不太吻合的。而在高度角E<10°时,延迟量可达15~20 m,而且3种模型的延迟差距相对较大,因此进一步证明了本文的观点,即可以根据高度角的不同选择比较好的算法。
(2)具体实现
本文利用北京测站接收到的G03的数据作进一步分析,北京测站观测G03的时间是从2010-12-06T 18∶54—2010-12-07T 01∶10,由于 IGS 观测数据采样间隔为30 s,共753个采样点;而IGS精密星历数据采样间隔为15 min,只包含25个采样点。因此需要对精密星历数据进行内插拟合。常用的内插拟合法主要有拉格朗日多项式法、牛顿多项式法、切比雪夫多项式法及三角多项式法。综合比较后,本文采用拉格朗日插值法对精密星历数据进行拟合[10]。图2为插值之前坐标数据的变化,而图3为利用插值之后的变化。
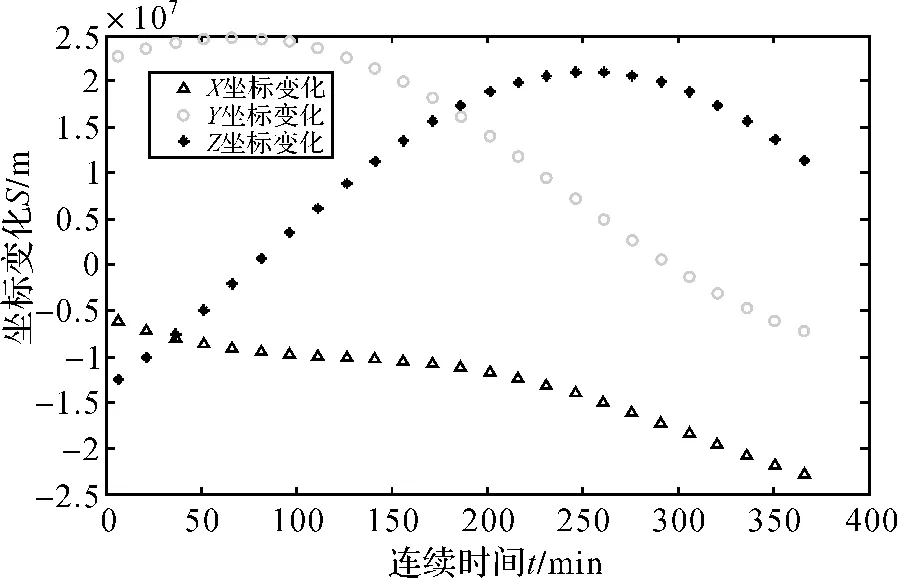
图2 地形坐标系下原始坐标在插值之前的变化
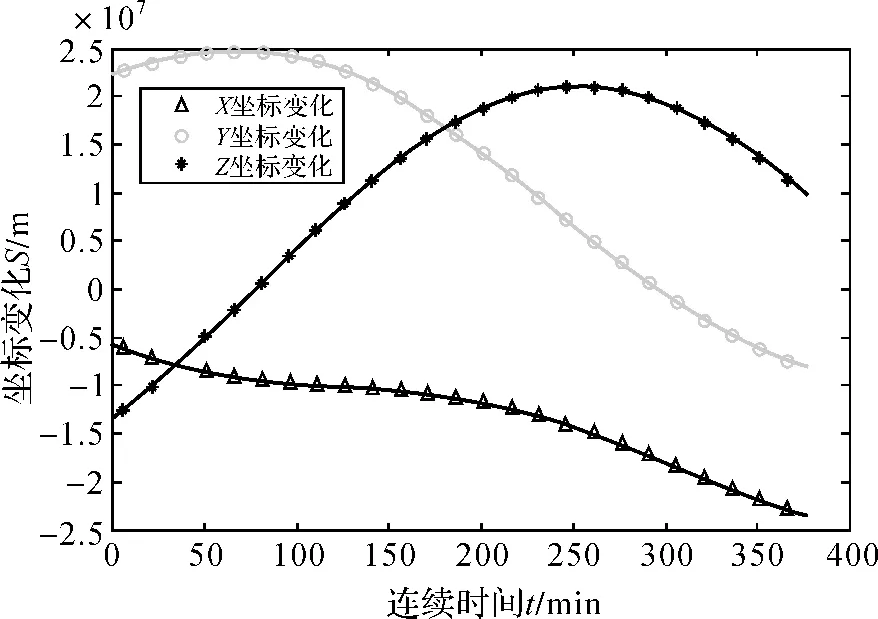
图3 地形坐标系下原始坐标在插值之后的变化
可以看出,利用拉格朗日多项式插值法可以很好地拟合卫星坐标的变化轨道。本文利用插值出来的数据,可以计算出高度角,如图4所示,从图中可以看出高度角随时间的变化趋势为一近似对称的抛物线,最小值约为5°,最大值约为83°。再结合测站的大气压、温度、水汽压数据,就可以很好地模拟出3种模型随高度角变化的规律,如图5所示,图中共有采样点753个,得到的图形与图1非常相似,也再一次验证了前面仿真图形的可靠性。由图5可以看出,3种模型在高度角E>45°时,几乎重合。只有Hopfield模型类似于图1中在接近天顶方向出现了“反弹”现象。而Saastamoinen模型与Black模型在高度角E>10°后曲线相当吻合,差距只有几厘米;在接近天顶方向时,差距甚至只有几毫米。

图4 经过插值后算出的高度角E的变化
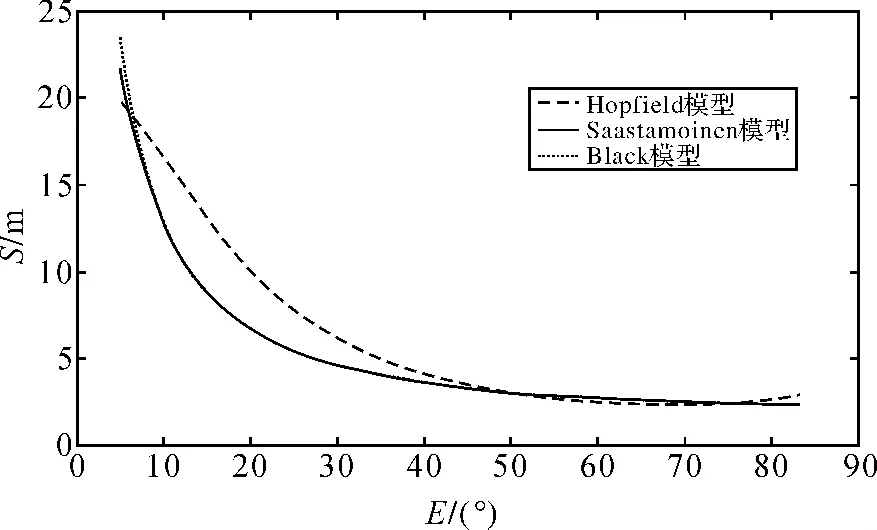
图5 插值后高度角的变化对3种模型的影响
2.模型分析
本文利用式(8)和式(9)对3种模型进行判断,为了在图形中更好地分析,考虑到高度角几乎为一个抛物线,本文将只利用一半的数据,而为了不失一般性,特选取后半段数据进行建模,结果如图6所示。
五、结 论
由图6分析可知,应根据高度角的不同选择合适的模型,具体结论如下:
1)3种模型算出的对流层延迟曲线趋势大致相同,只有Hopfield模型由于公式本身的缺陷,导致在天顶方向有反弹现象。
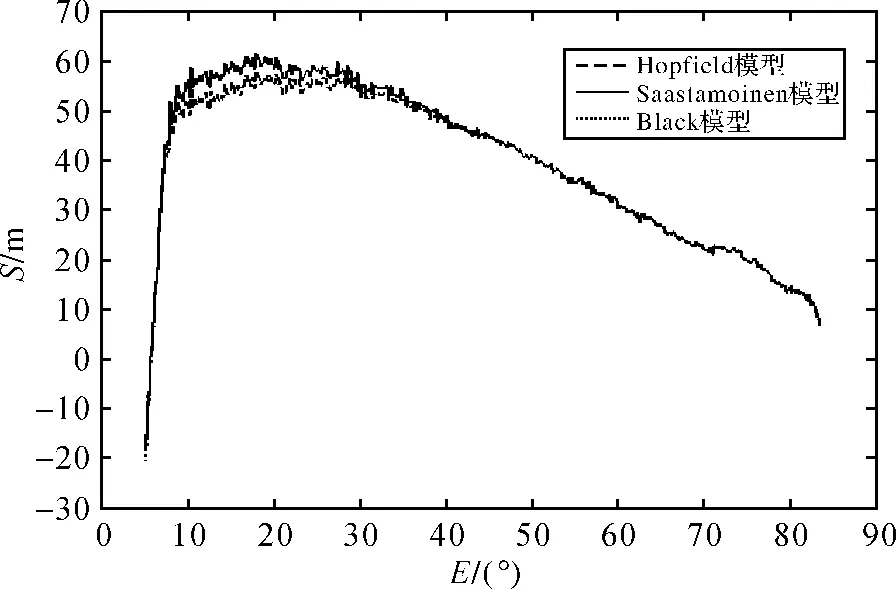
图6 利用式(8)得出的3种模型的差别
2)当高度角为6°~23°时,Hopfield模型与另外两种模型差异较大,约有几米;而Saastamoinen模型与Black模型差距相对较小,差距在几分米范围内。相比之下,取Saastamoinen模型较为精确。
3)在高度角为23°~50°时,3种模型的差距逐渐减小,最终只有几厘米甚至毫米级别的差距。相比之下,取Black模型更为精确。
4)在高度角为50°~75°时,3种模型差距几乎保持恒定,可在分米范围内波动。相比之下,取Hopfield模型更为精确。
5)在高度角为75°~83°时,由于Hopfield模型出现反弹,导致与其他两者差距逐渐变大,Saastamoinen模型与Black模型均能达到2.32 m,差距仅有2 mm。相比之下,取Black模型更为精确。
6)对于高度角小于10°时,3种模型的变化都比较剧烈,因此精度需要进一步研究。
因此,本文在最后根据以上结论编写出由高度角的不同选取不同模型的算法,效果如图7所示。
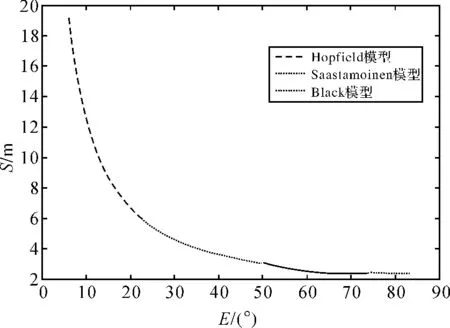
图7 根据不同高度角选择适当模型的综合算法
[1]李昭,邱卫宁,邱蕾,等.几种对流层延迟改正模型的分析与比较[J].测绘通报,2009(7):16-18.
[2]霍夫曼-伟伦霍夫,利希特内格尔,瓦斯勒.全球卫星导航系统GPS,GLONASS,Galileo及其他系统[M].程鹏飞等,译.北京:测绘出版社,2009:99-104.
[3]HOPFIELD H S.Two-quadratic Tropospheric Refractivity Profile for Correcting Satellite Data [J].Journal of Geophysical Research,1969,74(18):4487-4499.
[4]HOPFIELD H S.Tropospheric Effect on Electromagnetically Measured Range:Prediction from Surface Weather Data[J].Radio Science,1971,6(3):357-367.
[5]杨力.大气对GPS测量影响的理论与研究[D].郑州:信息工程大学,2001.
[6]SAASTAMOINEN J.Contributions to the Theory of Atmospheric Refraction:Part II.Refraction Corrections in Satellite Geodesy [J].Journal of Geodesy,1973,107(10):13-34.
[7]王新龙,李亚峰.GPS定位中4种对流层延迟修正模型适应性分析[J].电光与控制,2008,15(11):5-9.
[8]BLACK H D.An Easily Implemented Algorithm for the Tropospheric Range Correction[J].Journal of Geophysical Research,1978,83(B4):1825-1828.
[9]卡普兰.GPS原理与应用[M].寇艳红,译.2版.北京:电子工业出版社,2010:224-226.
[10]彭泽泉.GPS精密星历拟合方法的研究[J].测绘科学,2010,35(Sl):63-65.
——环地平弧&环天顶弧

