基于坝体沉降监测的ν-SVR参数优化方法研究

丛康林，岳建平，席广永

（1.山东农业大学测绘工程系，山东泰安 271018；2.河海大学测绘科学与工程系，江苏南京 210098；3.郑州轻工业学院计算机与通信工程学院，河南郑州 450002）

一、引 言

近年来，支持向量机（support vector machine，SVM）以其最小化的结构风险、较强的泛化能力等优势，越来越成为机器学习的热点，并被应用到模式识别、回归预测等众多的研究领域中。支持向量机性能的优劣关键在于其参数选取的是否合理。本文将支持向量机回归（support vector regression，SVR）算法应用到坝体沉降监测中，分析了各参数对回归预测精度的影响规律，并分别采用基于交叉验证的格网优化法和粒子群优化法进行参数寻优，对比分析了两种方法的效率、精度及可靠性。

二、ν-SVR参数的种类及作用

ν-SVR是在标准支持向量机ε-SVR的基础上改进而来的，用一个数量上有意义的参数ν来代替经验误差ε，建立能够自动计算ε的ν-支持向量回归机，通过核函数进行映射，构造高维空间中的线性回归函数f（x）=ωφ（x）+b，与ε-SVR不同的是，这里选定了另外一个参数ν，把最优化问题修改成［1］

与ε-SVR不同的是，这里的ε是作为二次规划问题的变量出现的，它的值将成为解的一部分，从而达到避免人为确定ε的值的目的。

将式（1）转换为对偶形式为

选择位于开区间（0，C/l）中的两个分量和以及它们所对应的支持向量yj和yk，则可求出偏置b

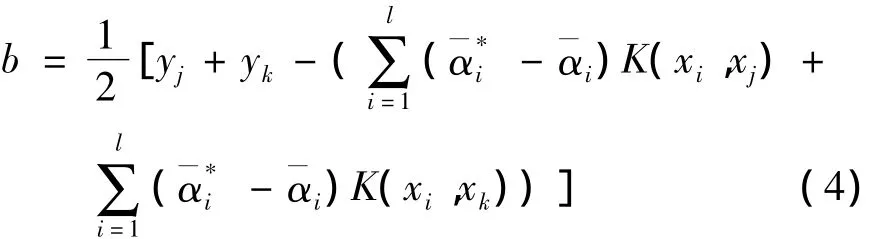
其中，参数ε作为最优化问题的解也被随之求出

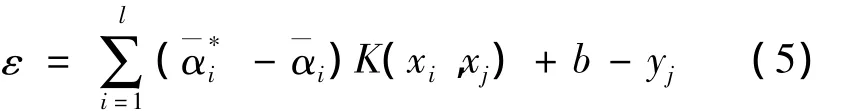
根据ω、b确定的回归决策函数为

众所周知，SVR的推广性能取决于一组好的参数，在ν-SVR中主要指的是惩罚参数C、核函数参数（简称核参数）及参数ν。

1.惩罚参数C

惩罚参数C为某一指定的正常数，其作用是对错分样本的惩罚程度进行控制，以达到在错分样本的比例和算法的复杂程度之间“折中”的目的，即调节学习机器置信范围和经验风险之间的比例［2］。

惩罚参数C越小，则对超出经验误差的样本惩罚越小，使机器学习的复杂度越低，导致训练误差变大，从而经验风险也就越大，表现为欠学习；反之，C值越大，经验风险越小，系统的泛化能力变差，表现为过学习。特别地，当C超过一定值时，SVM的复杂程度达到了数据子空间所允许的最大值，此时经验风险和推广能力几乎不再变化。

2.核函数参数

当选定某一核函数后，核参数的值便决定了核函数的特征空间，即核函数、映射函数及特征空间三者是一一对应的［3］。核参数的改变实际上是隐含地改变了映射函数，从而改变了样本数据子空间分布的复杂程度，也就是改变了特征空间线性分类面的最大VC维，从而决定了特征空间中线性分类超平面所能达到的最小经验误差。

3.参数ν

参数ν是对不敏感误差参数ε的改进，用一个数量上有意义的参数ν（ν∈（0，1））代替ε（ε∈（0，+∞））。ν表达的是错分训练样本数占总样本数的上界和支持向量的个数占总训练样本数的份额的下界［4］。原来的经验误差ε控制着不敏感带的宽度，影响着支持向量的数目，ε值越大，回归估计的精度越低，支持向量的数目越少，反之亦然。由于ν是从ε变换而来的，因此ν也间接影响着回归的精度和支持向量的数目。

三、参数选择的方法分析

目前，常用的评价SVM性能的方法为K折交叉验证法（K-cross validation，K-CV），其基本思想是:将原始数据均匀分成K组，即产生了K个子集，将每个子集分别作为一次验证集，余下的K-1个子集作为训练集，分别进行训练验证，用这K次验证精度的平均值作为SVM的性能指标。在某种意义下将原始数据进行分组，一部分作为训练集，另一部分作为验证集，先用SVM对训练集进行训练，再利用验证集来测试模型的优劣，以此作为SVM性能的指标。K-CV法可以有效地避免过学习和欠学习状态的发生，是目前应用较多的一种方法。

1.试凑法

在确定了SVM模型和核函数的情况下，首先对初始的惩罚参数C和核参数赋一任意的初始值，然后进行SVM训练和测试，根据得到的测试精度优劣对各参数进行人工调整并重新赋值，重新训练测试，由于参数变化对测试精度的影响遵循一定的规律，试凑法的参数调整有一定的规律可循。这样，经过不断重复验证，可寻求满意的参数。

试凑法是SVM参数寻优方法的基础，也是目前较常用的一种方法，在精度要求不是很高的情况下可以达到要求，虽然参数选择有一定的规律可循，但是主要依靠经验调整参数，需要人工进行大量试算，具有一定的盲目性，当需要调整幅度较大时，调整次数较多，实验繁杂，效率低。

2.格网法

格网法（Grid法）依托于计算机的快速运算性能，将各个参数在其取值范围所构成的格网中进行遍历，从中选取精度最好的节点所对应的参数为最优参数。为了提高遍历区间通常以log2（）的步长作为格网间隔［5］，参数选择结果的优劣与所划分格网的密度密切相关，格网间隔越小，遍历的参数就越精细，得到最优参数的可能性就越大，反之亦然。但是，如果将格网间隔划分得过小，计算机需要遍历的点就很多，势必影响计算速度，为此，通常把整个遍历寻参的过程分成两步或多步进行，以提高运行效率。具体操作过程如下:首先选取步长较大的值作为格网间隔进行参数寻优，此过程为粗选，粗选能从较大的参数范围寻找最优的参数，此过程确定了参数所在大致的取值范围；然后在粗选确定的范围内，以较小的步长作为网格间隔，再次进行训练测试，以选取更优的参数，此过程称为细选。这样两步下来就基本能够确定优化参数的值，若需要更加细致地进行参数遍历，可以再进行多次的细化步长，以筛选到理想的参数。

3.粒子群优化算法

粒子群优化算法（particle swarm optimization，PSO）是智能优化算法中较为快速有效的一种算法，支持向量机的参数寻优问题可以看做是在由各个参数的值域组成的多维空间（本文中为三维空间）中求解一个全局最优解问题，最优解条件就是上面交叉验证法中的精度指标。

对于粒子群算法的支持向量机参数寻优问题，每个粒子个体对应着支持向量机的各个参数，以各参数下的支持向量机模型的推广预测能力作为个体的适应值，通过粒子群算法可以同时快速获取推广预测能力最好的支持向量机各参数。

四、参数优化选择算例分析

西霞院反调节水库是小浪底水利枢纽的配套工程，位于黄河中游距小浪底水利枢纽约16 km处。取其混凝土坝段为研究对象来分析SVR参数寻优方法，根据坝体2005年4月至2006年3月的监测资料，利用2005年4月至2005年9月共40期实际监测的数据作为SVR模型的学习样本进行训练，构建预测模型，对2005年10月至2006年3月共20期的坝体沉降量进行预测，并与实际观测的沉降量进行分析比较。

由于参数寻优的试凑方法在很大程度上具有一定的盲目性，不便于科学地分析研究，因此本文只对格网法和粒子群算法进行比较研究。

1.基于Grid法的参数选择模型

本文采用ν-SVR的方法进行回归预测，采用RBF核函数，故需要选择的参数包括惩罚参数C、RBF核函数的宽度σ和参数ν。因此，以各参数为基准构造三维空间的格网，使3个参数在空间格网中遍历，通过对训练集交叉验证的评价精度来获得最好的参数值。由于参数C和σ的取值范围是（0，+∞），为使所构造的格网间隔较大，采用log2C和log2σ对数形式构造格网，这样如果log2C和log2σ取值在［-10，10］内，C和σ取值便能够达到［0.000 976，1024］的跨度，大大提高了遍历的效率。

取坝体的温度、时效、压应力、孔隙水压力、孔隙水压力水头、上游水位和坝体浇注高度为特征，先以较大的步长构造格网进行参数的粗选，得到参数所可能取值的大致区域，然后进一步细化网格，进行参数的细选，这样经过两次或多次细化网格便确定了3个参数的值。

图1分别为采用Grid法进行参数寻优的粗选和细选在log2C和log2σ面投影的等值线图。

根据Grid法获得的3个参数的值分别为:C=724，σ=0.08，ν=0.2。用获得的3个参数对后面20期的坝体沉降量进行预测，得到的结果如图2所示。

2.基于PSO法的参数选择模型

根据粒子群算法的基本思想，以3个参数C、σ、ν作为3个微粒，在三维解空间中进行飞行，以训练样本中交叉验证的最小均方误差作为适应度值，种群规模为20，终止迭代次数为200，得到适应度变化过程线和各参数的最优取值位置（如图3所示）。其中，圆点表示微粒在种群中的局部最优解的位置，十字表示最终确定全局最优解的位置。

图1 Grid法参数选择等值线图

图2 Grid法参数寻优的训练预测图

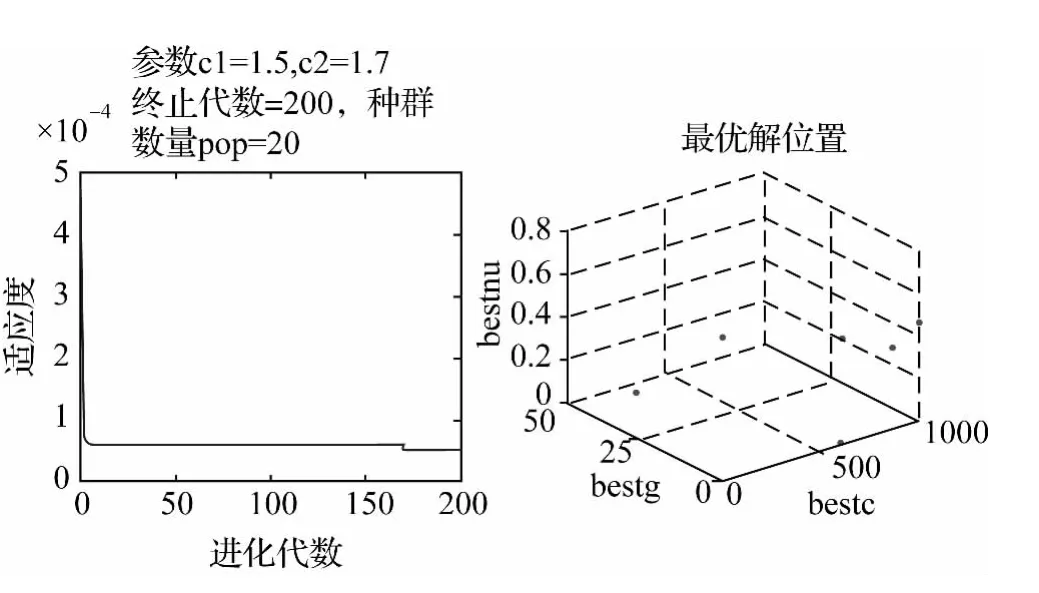
图3 PSO法适应度及参数最优位置示意图

PSO法获得的3个参数的值分别为:C=1000，σ=0.45，ν=0.45。根据获得的参数建立模型，对后面20期的坝体沉降量进行预测，如图4所示。

3.两种参数选择方法精度的对比分析

在选择了合适的各参数后，根据训练集建立ν-SVR回归模型，并对将来的值进行预测，为了检验模型预测效果的准确性，采用实测值来进行检验，根据以下评价指标进行精度的评定。

图4 PSO法参数寻优的训练预测图

1）均方误差

2）平均绝对百分百比误差

式（7）、式（8）中，f（xi）表示模型预测值；yi表示实测值；n表示样本的数量。

Grid法和PSO法进行参数寻优的结果及各项评价指标见表1。

表1 Grid法和PSO法参数寻优结果

五、结 论

从以上信息可以看出，Grid法经过多次细化网格进行参数选择的结果虽能达到较好的精度，但是相比PSO法仍存在不足之处，经比较得出以下结论:

1）Grid法中格网的范围选取对参数寻优影响较大。理论上在大的范围内能够保证找到较优参数，但是格网的范围过大则需要消耗过多的时间，而范围过小则不能保证找到较好的参数，因此通常需要根据经验调整；相反，PSO法在算法设计时已经确定了足够大的初始参数范围，并且通过自动调整微粒的飞行速度和位置来进行参数寻优，保证了确定合适参数的可能性。

2）Grid法消耗的时间还与格网的密度有关，并且通过多步细化格网来进行参数的寻优，所消耗的时间具有不确定性；PSO算法每次消耗的时间是由种群数量和终止代数决定的，而这两项在算法确定的情况下是固定不变的，因此对于任何样本的训练所消耗的时间是基本相同的。

3）支持向量机的参数选择实际上是一个最优化的问题，Grid法通过遍历的方式来寻优，考虑到遍历效率的问题而不可能把网格划分得过于密集，因此最终寻到的参数是全局最优的可能性较小；而PSO法则是从随机解出发，通过迭代追随当前搜索到的最优值来寻找全局最优解，避免了人为选择参数的盲目性，提高了模型的训练速度和预测推广能力。

［1］ 邓乃扬，田英杰.支持向量机——理论、算法与拓展［M］.北京:科学出版社，2009.

［2］ 邓小文.支持向量机参数选择方法分析［J］.福建电脑，2005（11）:30-31.

［3］ 王睿.关于支持向量机参数选择方法分析［J］.重庆师范大学学报:自然科学版，2007，24（2）:36-38，42.

［4］ VAPNIK V N，CHERVONENKIS A Y.The Theory of Pattern Recognition［M］.Moscow:［s.n.］，1974.

［5］ HSU C W，CHANG C C，LIN C J.A Practical Guide to Support Vector Classification［R］.Taiwan:National Taiwan University，2003.