最小不确定度估计及其在测量数据处理中的应用

陈 伟，张 践

（1.武汉科技大学城市建设学院，湖北武汉 430074；2.武汉大学测绘学院，湖北武汉 430072；3.武汉苍穹数码仪器有限公司，湖北武汉 430065）

一、引 言

笔者在文献［1］中提出了最小不确定度估计理论。该估计理论是以模糊数理论为其理论基础，将观测值看做模糊数，以模糊数为研究对象，并结合计量部门采用测量不确定度评定测量结果的做法，用模糊幅度代替A类评定或B类评定来衡量不确定度，进而用不确定度作为评定观测结果的质量指标，即从与传统的参数估计思路完全不同的角度去研究测量数据处理的理论与方法。

二、模糊数与不确定度

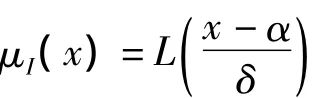
不确定度是与测量结果相关联的参数，用于表征合理地赋予被测量值的分散性，即不确定度是一个表示测量结果中用于说明测得值所处范围的参数。模糊幅度就是描述测得值所处范围的一个数，模糊幅度和不确定度不同于测量误差，没有正负之分。因此，用模糊幅度去衡量测量结果的不确定度是合理的。

三、最小不确定度估计模型的建立

当函数模型是非线性模型时，用数学公式表示为

式中，F（X）=［f1（X）f2（X） …fn（X）］T，为未知参数向量X的函数。

当函数模型是线性模型时，用数学公式表示为

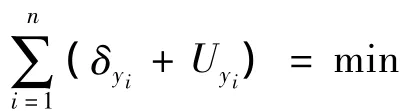
综上所述，可得最小不确定度估计的参数估计模型为

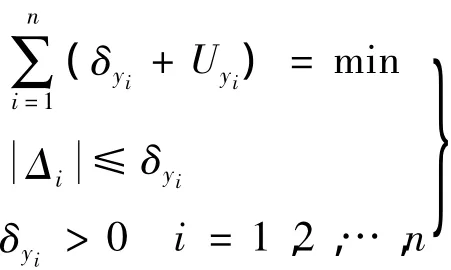
对于不同的参照函数，观测值的隶属函数（yi）是不同的。针对几种常见的参照函数，将其对应的隶属函数代入最小不确定度估计的参数估计模型中可分别得到基于三角模糊数、余弦模糊数、抛物线模糊数的最小不确定度估计模型。

1）基于三角模糊数的最小不确定度估计模型为

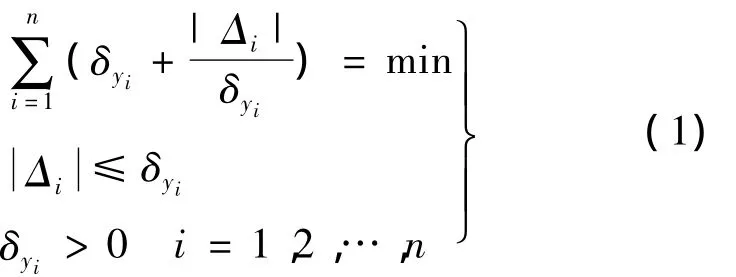
2）基于余弦模糊数的最小不确定度估计模型为

3）基于抛物线模糊数的最小不确定度估计模型为

分别解算以上3种不同的估计模型，则可得到分别对应三角模糊数、余弦模糊数和抛物线模糊数的未知参数X的估值和观测值的不确定度。

四、最小不确定度估计在测量数据处理中的应用

本例取自文献［2］第107页例［5-8］，今有测边网如图1 所示。网中A、B、C、D为已知点，P1、P2、P3、P4为待定点，同精度观测了13条边长。已知点坐标和待定点近似坐标见表1，观测边长见表2，求待定点的坐标平差值。

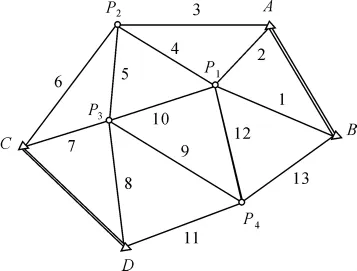
图1

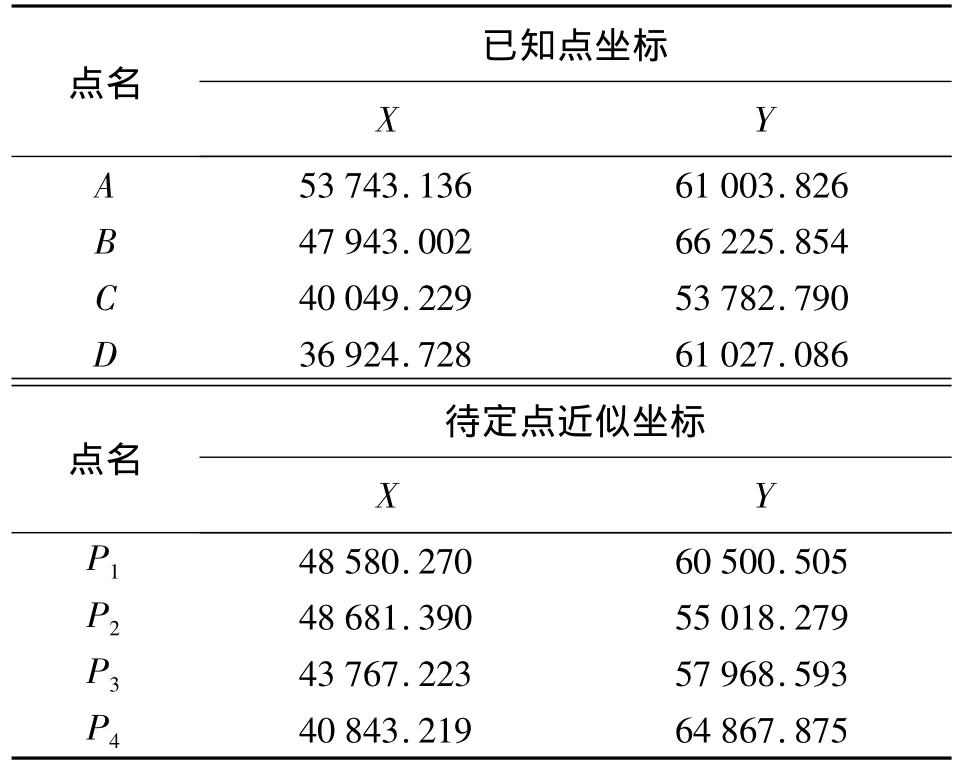
表1 已知点坐标和待定点近似坐标

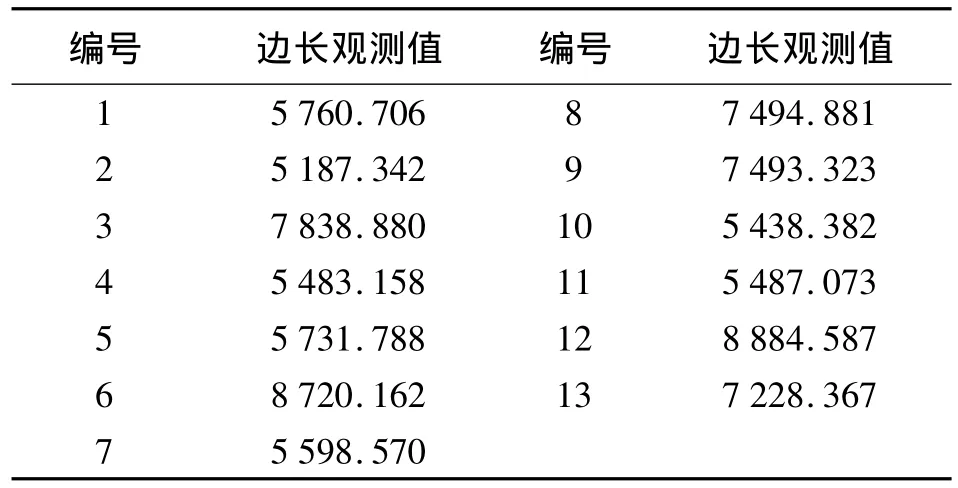
表2 边长观测值 m

测边网的观测方程为

所以可得

将上式代入式（1）～式（3）中可分别得到基于三角模糊数、余弦模糊数和抛物线模糊数的最小不确定度估计模型。其中，待定点的坐标和边长观测值的不确定度均为未知参数，参数个数为21个。对于3种不同的模糊数，给定相同的初始条件，用遗传算法求解非线性规划问题即可得待定点坐标和观测值的不确定度。计算结果见表3～表6，表中还将最小不确定度估计结果（MU）与最小二乘估计结果（LSE）进行了比较。

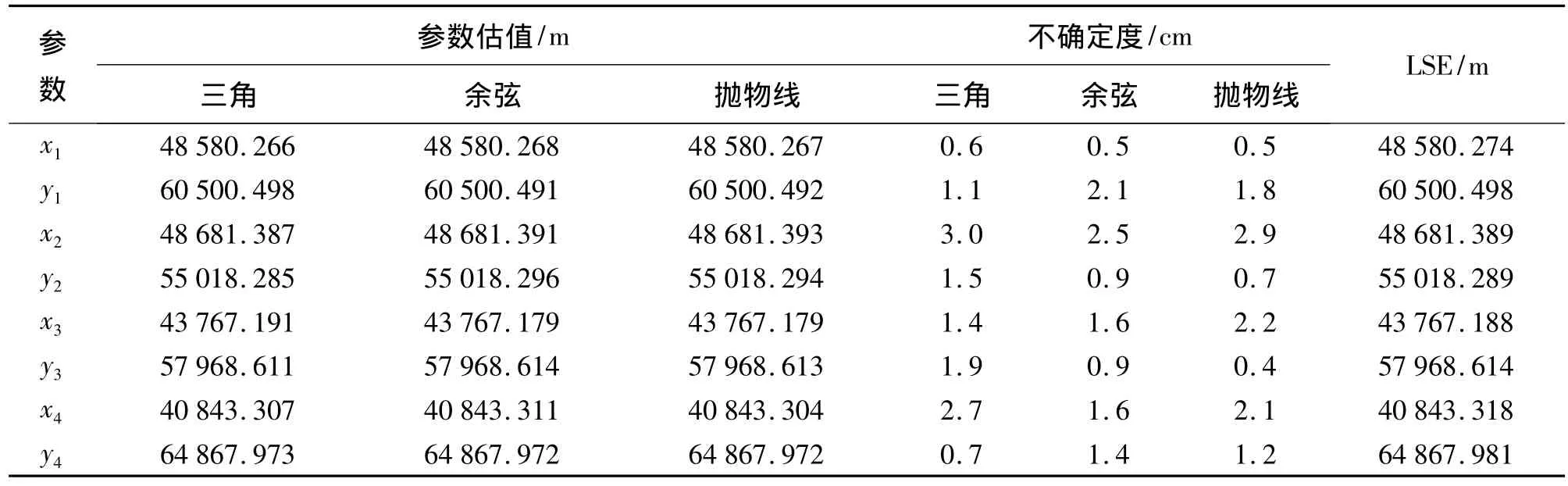
表3 不同模糊数对应的参数估值

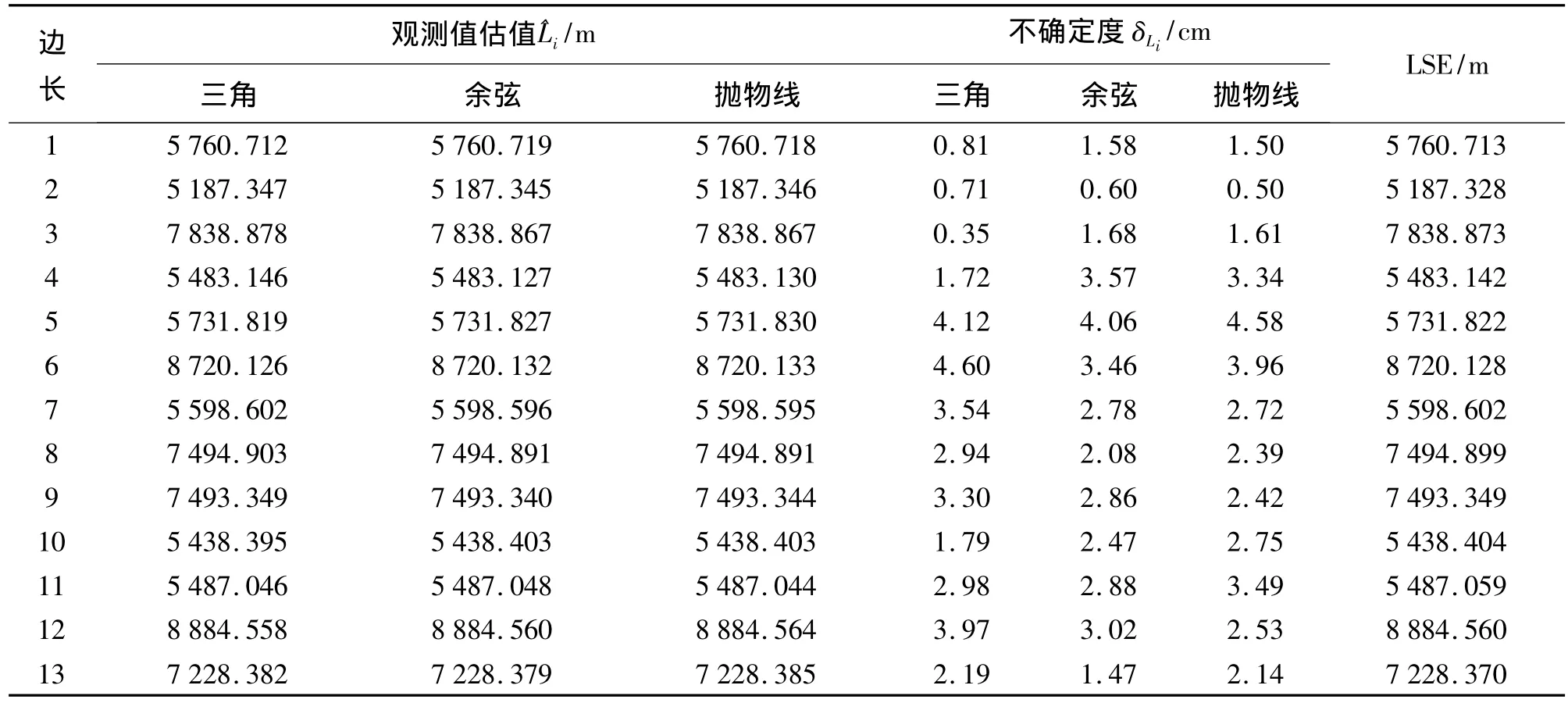
表4 不同模糊数对应的观测值估值

表5 参数估值与最小二乘估值的较差表 mm

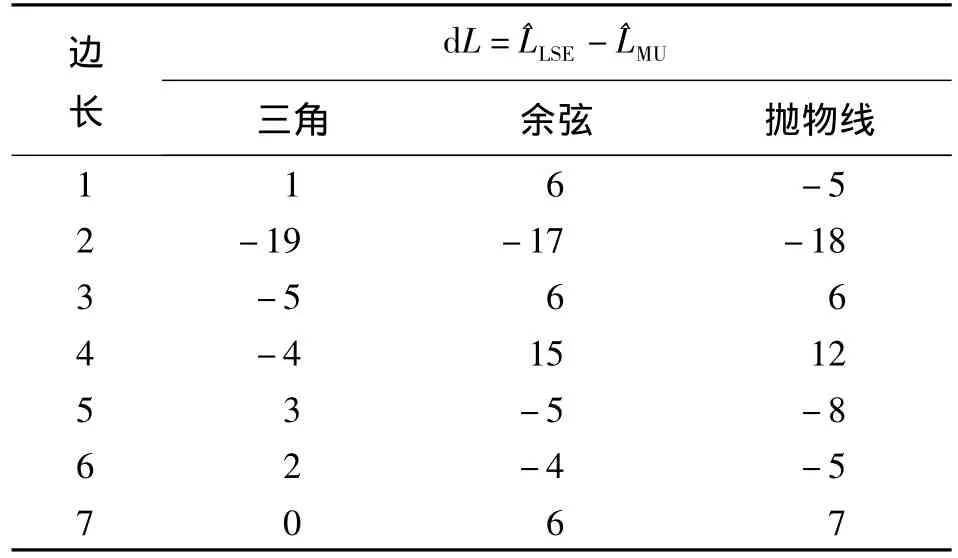
表6 观测值估值与最小二乘估值的较差表 mm

续表6 mm

计算结果表明，用三角模糊数、余弦模糊数和抛物线模糊数3种不同的模糊数计算出来的待定点坐标是大致相同的，且与最小二乘估计的结果很接近。

五、结束语

本文提出的最小不确定度估计打破了传统参数估计方法处理随机变量的局限，将观测值看作是以其真值为对称中心的对称模糊数，从而避免了将观测值的不确定性看作随机变量带来的问题，直接处理测量数据的不确定性。通过对算例的结果进行分析，并与最小二乘估计的结果进行对比，表明最小不确定度估计用于测量数据处理是合理可行的。如何将其广泛地应用于测量数据处理领域将是笔者接下来要进一步研究的工作。

［1］ 陈伟，王新洲.最小不确定度估计原理及其病态问题解法研究［J］.武汉大学学报:信息科学版，2008，33（7）:752-754.

［2］ 武汉测绘科技大学测量平差教研室.测量平差基础［M］.3版.武汉:武汉测绘科技大学出版社，1999.

［3］ 王新洲.最小不确定度约束下的极大可能性估计［J］.测绘工程，2003（1）:5-8.

［4］ 王新洲，史文中，王树良.模糊空间信息处理［M］.武汉:武汉大学出版社，2003.

［5］ 李金海.测量理论与测量不确定度评定［M］.北京:中国计量出版社，2003.

［6］ 王新洲，史文中.极大可能性估计［J］.测绘学报，2003，32（3）:33.

［7］ 陈伟.最小不确定度估计理论及其应用［D］.武汉:武汉大学，2005.