对流层延迟参数与坐标参数的相关性研究

徐宗秋，徐爱功，高 扬，2，徐彦田，徐辛超

（1.辽宁工程技术大学测绘与地理科学学院，辽宁阜新 123000；2.卡尔加里大学地球空间信息工程系，加拿大T2N1N 4）

一、引 言

精密的对流层延迟模型不仅是空间大地测量技术如GNSS、VLBI和DORIS等进行精密定位的必要条件，也是GPS气象学中的研究重点［1-2］。对流层干延迟变化缓慢，利用先验模型精度可达到亚毫米级。对流层湿延迟随时空变化复杂，任何湿延迟模型都不能准确地描述其变化，模型改正后的残差仍会对坐标垂直分量产生严重影响。随着GNSS卫星的不断增多，利用参数估计法确定对流层湿延迟将具有更高的精度，其应用日趋广泛［3］。然而，对流层延迟与坐标垂直分量参数存在高度的相关性，制约了参数估计精度的进一步提高，特别是在动态定位中，对流层延迟参数估计是一难题［4］。

为了解除参数相关，M.Rothacher建议利用低高度角下的观测数据来进行梯度估计［5］，Yong Won Ahn等则根据两参数是天顶距相关的特性将其合为一个参数［6］，这些方法在相对定位中均提高了参数估计精度。但由于在精密单点定位中相关研究较少，因此本文采用IGS站观测值数据及相应的最终精密星历与钟差，利用随机卡尔曼滤波进行精密单点定位解算，得到对流层延迟与坐标垂直分量参数误差，并对其相关性进行定性与定量分析。

二、数据处理方法

1.对流层延迟估计

GPS信号经过地球大气层传播至GPS接收机时，会受到对流层的影响，对流层延迟分为干延迟（约90%）和湿延迟（约10%）。对流层延迟的影响与卫星的高度角有关，对于一个海平面上的中纬度测站，GPS卫星信号经过对流层在天顶方向上的干延迟可达2.3 m，湿延迟约0.01～0.8 m，当高度角为15°时的总延迟量可达25 m。干延迟模型精度达到亚毫米级，而湿延迟由于主要受空气湿度影响而具有较强的时间和空间性，仅用模型改正不能满足高精度定位要求，因此需对湿延迟进行估计。

利用非差精密单点定位技术估计对流层延迟的独特优势体现在:估计模型简单、能直接得到高精度的绝对延迟、时间分辨率高、全天候观测等［7］。观测值中的电离层延迟可通过双频信号组合进行消除，而对流层湿延迟则可通过引入未知参数进行估计。在测站近似坐标 （X0，Y0，Z0）线性化后的载波相位观测方程为

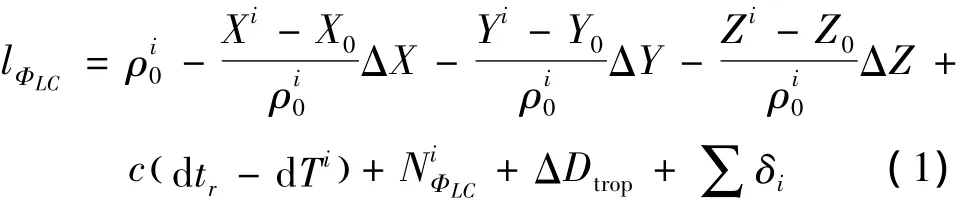
一般的对流层延迟模型是建立在大气各向均质的假设上，但实际上大气各向非对称，因此引入了水平梯度模型［8］，顾及水平梯度模型的对流层延迟模型为

式中，E为卫星高度角；ΔDz，dry为对流层天顶干延迟，由 Divas模型计算；ΔDz，wet为对流层天顶湿延迟，待估参数；Mdry（）E与Mwet（）E分别为干湿延迟投影函数，由GMF投影函数计算；MHG（）E为梯度投影函数，由Mwet（）E推导；φ为方位角；GN和GE分别为水平梯度北方向和东方向的分量，待估参数。

Divas（1985 年）对流层天顶干延迟 ΔDz，dry的计算公式为

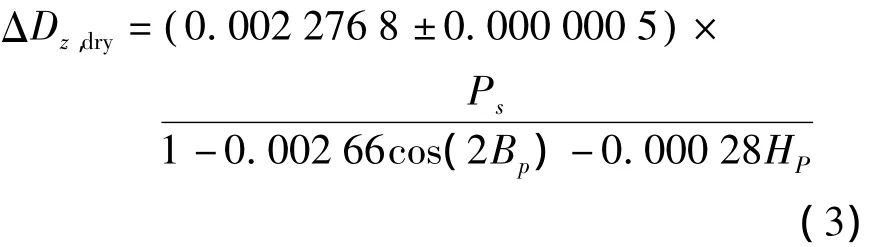
式中，Ps为地面大气压，由GPT模型计算得出；Bp为测站纬度；Hp为测站高程。

全球投影函数（global mapping function，GMF）的干湿分量都采用了三项连分式形式，设其基础公式为［9］

则GMF干湿分量投影函数分别表示为

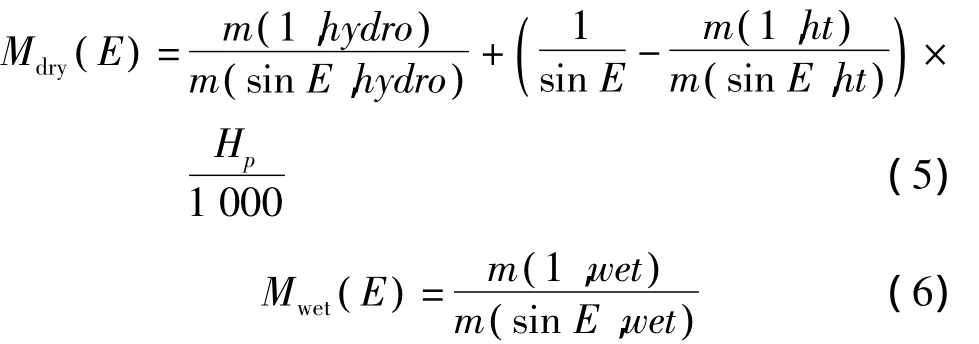
式中，ay、by、cy为参数；下标y表示不同类型的参数，其值或为常数或由经验公式计算得出；Hp为测站高程。

梯度投影函数的计算公式为

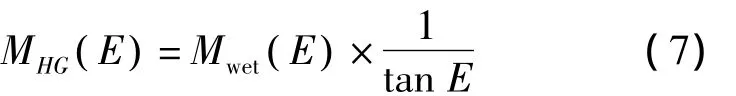
非差相位精密单点定位中要估计的参数包括测站坐标、接收机钟差、对流层天顶湿延迟、对流层梯度参数及组合模糊度。静态时测站坐标为估计常量，动态时为时变量，接收机钟差为白噪声，对流层天顶湿延迟及梯度参数采用随机游走的方法估计。采用随机卡尔曼滤波方法进行解算。

2.相关分析与回归分析

当将对流层延迟与坐标一起作为参数进行估计时，二者存在相关关系，制约了参数估计的精度，因此有必要对这一相关关系进行研究。相关关系是指两个变量或若干变量之间存在着一种不完全确定的关系，它是一种非严格的确定性的关系，对具有相关关系的变量进行量上的测定需要借助于函数关系。用分析指标对变量之间的密切程度进行测定的方法称为相关分析；运用相应的函数对存在相关关系变量进行定量统计分析的方法为回归分析［10］。

由概率论知识，两个随机变量之间的线性相关程度可以用相关系数来表示，其计算公式为

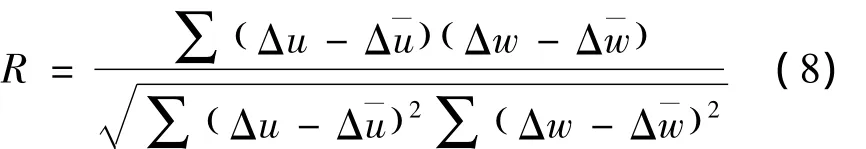
式中，R为相关系数；Δu和Δw为待检验的随机变量。

相关系数的取值范围是-1≤R≤1，正的表示正相关，负的表示负相关。利用相关系数判断相关关系的密切程度，通常0.5＜R≤0.8表示显著相关，0.8＜R≤1表示高度相关。

在判断两个变量具有线性相关的基础上可以进行一元回归分析，确定合适的表达式，以便进行估计和预测，一元回归方程为

式中，a为截距；b为回归系数。

根据最小二乘原理可以得出

评价回归方程拟合优劣的常用指标为判定系数和估计标准差。判定系数用来说明因变量的变化有多少可通过自变量得到解释，是衡量拟合模型优劣的重要分析指标。判定系数的值为R2，R2越接近1说明回归模型拟合的越优。估计标准误差是因变量各实际值与其估计值之间的平均差异程度，表明估计值对各实际值代表性的强弱，其值越小，回归方程的代表性越强，用回归方程估计或预测的值越准确。估计标准误差的公式为

式中，S为估计标准误差；Δu为实际值；Δ为估计值。

三、试验与分析

试验采用IGS站观测值数据及相应的最终精密星历与钟差，利用随机卡尔曼滤波进行精密单点定位解算。以静态模式下得到坐标与对流层天顶湿延迟（SWZTrop）为真值，得到动态下坐标垂直分量误差（Δu）与对流层天顶湿延迟误差（Δw），并对Δu与Δw进行相关分析与回归分析。

1.数据来源

对流层湿延迟与地理环境和季节密切相关，为了验证其与坐标垂直分量相关性的一般性，选择了具有代表性的两个IGS站和两个月份的数据。2011年2月8—14日上海shao站与新疆guao站的数据，2011年8月8—14日shao站的数据，两测站高差达2000多米，数据分为3组。

2.结果与分析

对于shao站和guao站的3组数据进行处理，得到对流层天顶湿延迟及其误差与坐标垂直分量误差的关系分别如图1～图3所示。卫星截止高度角为7.5°。

图1 对流层天顶湿延迟及其误差与坐标垂直分量误差（2月shao站）

图2 对流层天顶湿延迟及其误差与坐标垂直分量误差（8月shao站）

图3 对流层天顶湿延迟及其误差与坐标垂直分量误差（2月guao站）

从图1～图3中可以看出对流层天顶湿延迟随时空变化的复杂性。对流层天顶湿延迟误差（Δw）与坐标垂直分量误差（Δu）总体上都小于0，统计结果见表1。

表1 误差统计m

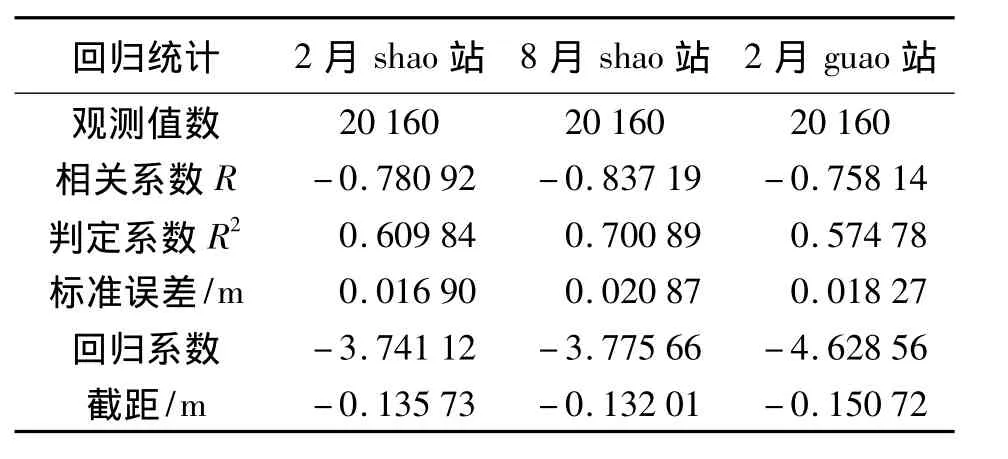
表2 回归统计

从表1中可以看出，Δw与测站位置和季节有关，Δw平均值为1 cm左右，最大值为4 cm左右；Δu的平均值为10 cm左右，最大值为30 cm左右；Δw与Δu的波动幅度明显不同。从图1～图3中亦可看出，Δw与Δu的波动幅度不同，但波动方向恰好相反，对其进行了相关性分析与回归分析。回归统计见表2，Δw与Δu的散点图与回归直线分别如图5～图7所示。

图4 Δw与Δu散点图及回归直线（2月shao站）

图5 Δw与Δu散点图及回归直线（8月shao站）

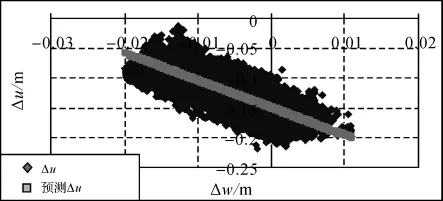
图6 Δw与Δu散点图及回归直线（2月guao站）

图7 不同截止高度角下的相关系数（8月shao站）

根据相关性原理，从表2中可以得出，Δw与Δu的相关性情况为，2月份shao站与guao站为显著负线性相关，但接近高度负线性相关。8月份shao站为高度负线性相关。这一相关性与测站位置和时间有关，但总体上为显著负线性相关。根据判定系数和标准误差指标，回归模型的拟合效果良好。回归系数在-4左右，即Δu波动幅度是Δw波动幅度的4倍左右。从图4～图6可以看出，散点均匀分布在回归直线两侧，回归模型的拟合效果良好。

对流层天顶湿延迟的估计与卫星截止高度角密切相关，以shao站8月份的数据为例，分析卫星截止高度角对相关系数的影响。为方便比较，相关系数取绝对值，结果如图7所示。

从图7可以看出，当截止高度角小于10°时，相关系数变化不大；当卫星截止高度角大于10°时，相关系数随截止高度角增加而减小。因此，截止高度角低时，参数相关性强。

四、结束语

对流层天顶湿延迟的精确确定对空间大地测量学及地基GPS气象学都具有重要的意义。仅用经验模型残差影响较大，必须利用参数估计法。然而对流层延迟参数（Δw）与坐标垂直分量参数（Δu）存在相关性，限制了估计精度的提高。

研究表明，Δw与Δu显著负线性相关，且Δu波动幅度是Δw波动幅度的4倍左右。低高度角下的观测值含有丰富的延迟信息，而此时Δw与Δu的相关性较强。充分利用参数相关的特点，提高参数估计精度，是进一步的研究内容。

［1］ STEIGENBERGER P，BOEHM J，TESMER V.Comparison of GMF/GPT with VMF1/ECMWF and Implications for Atmospheric Loading［J］.Journal of Geodesy，2009，83（10）:943-951.

［2］ 张小红，何锡扬，郭博峰，等.基于GPS非差观测值估计大气可降水量［J］.武汉大学学报:信息科学版，2010，35（7）:806-810.

［3］ TEKE K，BOEHM J，NILSSON T，et al.Multi-technique Comparison of Troposphere Zenith Delays and Gradients during CONT08［J］.Journal of Geodesy，2011，85（7）:395-413.

［4］ TREGONING P，HERRING T A.Impact of a Priori Zenith Hydrostatic Delay Errors on GPS Estimates of Station Heights and Zenith TotalDelays［J］.Geophysical Research Letters，2006，33（23）:1-5.

［5］ ROTHACHER M.Estimation of Station Heights with GPS［C］∥International Association of Geodesy Symposia.Berlin:Springer，2002:81-90.

［6］ AHN Y W，KIM D，DARE P.Estimation of Troposphere Decorrelation Using the Combined Zenith-dependent Parameter［C］.∥Proceedings of ION GNSS.Savannah:［s.n.］，2008:261-270.

［7］ 王勇，柳林涛，郝晓光，等.武汉地区GPS气象网应用研究［J］.测绘学报，2007，36（2）:141-145.

［8］ 李黎，匡翠林，朱建军，等.水平梯度和映射函数对PPP对流层延迟估计的影响分析［J］.工程勘察，2011（5）:52-56.

［9］ 徐杰，孟黎，仁超，等.对流层延迟改正中投影函数的研究［J］.大地测量与地球动力学，2008，28（5）:120-124.

［10］ 高雷阜，李伟.新编概率论与数理统计［M］.沈阳:东北大学出版社，2000:254-290.