关于Coulomb应力变化/扰动作用下的Dieterich余震触发机制的广义解
仲 秋,史保平
中国科学院大学,北京 100049
1 引 言
准确地获取地震的发生时间已成为震源物理研究中最为重要和根本的目标之一,然而到目前为止,对于该方面的探索仍然处于一个难以实现的阶段,尽管如此,主震发生后余震定位和时间确定的研究仍取得了许多的进展.地震触发过程和力学机制的探讨在近二十多年以来得到了广泛的研究和关注[1].我们知道,大震后通常伴随着大量的余震活动,余震的空间分布(至主震断层的距离)一般超过了主震断层的破裂尺度,而在时间上则反映在同主震前区域内地震活动性相比,研究区域内地震活动性的突然增加.Omori经验关系描述了余震序列随时间的发生频度,即主震后余震个数随着时间的推移而逐步减小的变化过程.Omori经验关系对于单位时间内大于某一震级的余震个数的描述满足n(t)=K/(t+c)p,其中K、p和c为常数,p值通常等于1.从统计上讲,尽管全球大多数地震满足该经验准则,但由于其缺乏相应的物理基础,在实际地震观测中,出现了很多不一致的情况.例如位于San Andreas断裂上的1989年Loma Prieta地震(MS6.9)与1811到1812年间美国中部的New Madrid地震(MS7.0-7.4)的余震时空分布有着明显的区别.前者余震多分布于主震后1~2年的时间内,而后者余震延续时间很长,而且大于4级的余震个数至今为止并无明显减少的趋势.
过去的几十年里,地震科学研究发现地震不论在近场(<2~3个断层长度)还是远场都可以触发(诱发)余震,余震的发生机制一般可分为静态和动态应力触发.前者可由主震的同震位移造成主断层内部以及周边的应力场变化,以及震后滑移和震后应力松弛;而动态触发则来自于地震应力波的辐射和传播所造成的周边断层的失稳,动态应力波的传播也可导致远距离的地震诱发.有关静态或动态触发机制的讨论至今仍是学术研究的一个重要课题.在目前的工作中,我们从Dieterich[2]的工作出发,探讨与静态应力触发相关的理论模型的发展,并将其用于对1976年唐山地震序列的拟合.
同震滑移后静态Coulomb应力变化的计算[3]已成为非常有用的手段,用于对余震活动性及其时空分布的定量化描述.主震后Coulomb应力变化取正值的区域一般对应了地震活动性的明显增加;反之,Coulomb应力变化的下降则对应了区域内地震活动性的减小,通常被称之为地震影区.虽然Coulomb应力变化模型已成功地应用于许多地震序列的模拟,包括Landers地震[4]和North Anatolian断层运动[5-6],但其局限性是明显的[7-9].例如,由Coulomb模型所计算的静态应力变化对于远场地震触发无法给出合理的解释.另一点值得商榷的是,Coulomb应力变化无法对Omori余震衰减过程进行定量化描述.例如,在Coulomb应力变化模型中,对于单个断层所受到的静态Coulomb 应力扰动量ΔCFF(Coulomb Failure Function),该断层的发震时刻可以得到提前或推后,其时间上的提前或推后量一般表示为[10]:
式中,Δτ和Δσ分别为作用于断层上的剪应力和有效正应力的扰动量(增量),μ为断层上的摩擦系数.该公式被广泛应用于对地震影区成因的解释和依赖于时间的地震预测中[6,11-12].在本文中,基于R-S摩擦关系和单自由度弹簧-滑块模型,我们将给出上述公式在应用中可能遇到的问题,并对其局限性做深入的讨论.
Dieterich[2]余震触发理论已广泛应用于对断层滑移和地震活动性关系的定量化描述.大震发生后,区域内余震发生率R可以直接同背景场地震活动性或地震发生率r和状态变量γ相关联,即有
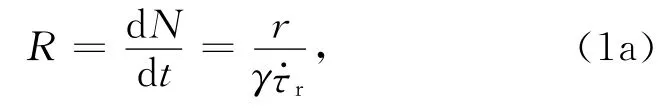
式中N为事件发生的个数,r 为背景场剪应力加载率.而状态变量γ随时间的演化过程则由(1b)式给出:
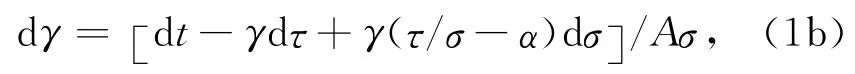
式中A和α为R-S本构关系中的常数(由实验结果所确定,下文将给出具体的意义).τ和σ分别为作用于断层上的剪应力和有效正应力.根据公式(1a)和(1b),Dieterich[2]得到了在给定静态剪应力扰动Δτ时余震发生率R的一般解:

公式(3)可以写成Omori定律的形式:R=a/(b+t)的形式,而公式(2)给出的是Omori定律当t/ta<1时的形式[2].该理论对Omori定律给出了定量化和合理的物理解释.而后在1996 年的文章中[13]给出Coulomb应力变化情形时的修正解,即将1994年[2]所给方程中的Δτ用ΔCFF 取代,但对于如何获得其结果则无任何明确的阐述.
本研究工作从最基本的宏观库仑摩擦准则出发,基于滑动速率和状态相依赖的摩擦定律,采用简单的力学模型获取断层内Coulomb应力的加载速率,阐述了余震发生率和其持续时间同Coulomb应力状态之间可能存在的相互联系.从简单的断层群体化概念模型出发,求取包括剪应力和正应力同时变化时,余震发生率R的基本解.在给定近似条件下,其结果同Dieterich[13]1996年给出的解是一致的.进一步,我们也将证明,如果断层的演化过程包括了R-S模型所述的三个阶段,即闭锁、成核/加速和同震过程,那么Coulomb模型中所提出的断层发震时刻提前或推后的解析表达式则应该对应于断层的闭锁阶段,而受到来自Coulomb应力扰动所造成的地震活动性的显著增加则应主要来源于断层成核/加速阶段.
2 理论模型
2.1 滑移速率和状态相依赖的摩擦关系
滑移速率和状态相依赖的摩擦本构关系为我们提供了一个基本框架以对断层内部复杂属性进行定量描述.该本构关系是由岩石力学实验结果所获得,并在断层演化和地震成核过程和断层破裂分析得到了广泛的应用.具体地讲,滑移速率和状态相依赖的摩擦定律还表达了稳态滑移过程中,观测到的瞬时速率与稳态速率之间的相关性.滑移速率和状态相依赖的断层内部摩擦应力的一般性方程由(4)式给出[14-15]:

其中,τ和σ分别为作用于断层上的剪应力和正应力,为沿断层面上的滑移速率.θi是与时间和滑动速率相关的状态变量,同时间t有相同的量纲,具体地描述了断层内部和接触时间相关的老化过程(Aging).参数μ0、A和Bi为实验所得系数.含星号的项为标准化的参考常量.Alog表征了类似于小形变的不规则体或障碍体产生于滑动面的黏性阻力.Bilog(θi/θ*i)表征了与接触时间成正比的两表面间的化学附着.对于状态变量θi的物理描述则来自岩石力学实验的结果,即状态变量θi与滑移速率和作用于断层面上的正应力σ有关,一般可表示为:

其中,Dci是临界滑动位移,αi是θi前的控制系数.在目前的研究中,为使问题简化而不失一般性,我们采用单个状态变量θ来描述断层随时间的演化特征.因此,公式(4)和(5)可分别改写为:

公式(6)和(7)被广泛应用于对断层运动学和动力学演化的研究中.
2.2 单自由度弹簧-滑块摩擦模型
假设断层的摩擦过程可由单自由度的弹簧-滑块模型所描述(图1),那么,作用于滑块接触面上的剪切摩擦应力τ可由(8)式给出:

图1 单自由度的弹簧-滑块模型τ和σN 分别为作用于断层上的剪应力和正应力,δ为沿断层面上的滑动位移,δ0为远场加载滑动位移,k为弹簧的有效弹性系数.Fig.1 Spring-Slide Block Model with kinematic equation of motionτandσNare the shear stress and normal stress acting on the fault,respectively.δis the sliding displacement along the fault plane,δ0is a far-field loading displacement,and kis the effective elastic coefficient of the spring.

公式(8)中k=Gη/l,为弹簧的有效弹性系数,与裂纹的长度l成反比[16],其中,G为剪切模量,η为描述裂纹的几何参数,一般取为1[17].为了使断层发生失稳成为可能,k<kc=(B-A)/Dc[18],δ0(t)为远场加载滑动位移.设定τ0为断层内部的初始剪应力.若远场剪切滑移加载速率δ·0(t)为常数且不等于0,那么,其剪应力加载速率可表达为=kδ·0(t).由此,公式(8)可改写为:

在给定的初始条件下,当Dc给定,数值求解方程(6)(7)和(8),得到断层移动的演化过程可由三个阶段所组成,如图2所示:1)稳定滑动阶段(断层闭锁时段);2)加速阶段;3)瞬态失稳阶段.地震的同震过程对应于第3阶段,即断层的动态破裂,通常可在几十秒到上百秒内完成.事实上,真实的断层演化实际上更为复杂,但一维模型则直观地描述了断层演化的基本过程.如果断层的运动形式确如图2所示,则上述模型的讨论对于我们更深入探讨地震的成因机制提供了最为基本的物理思路.
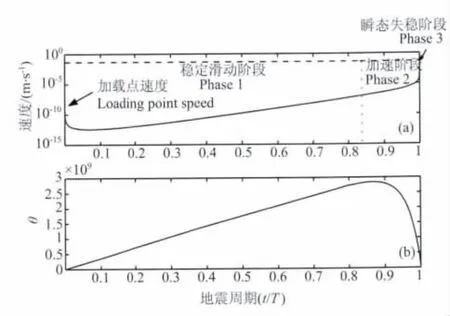
图2 数值模型给出的断层滑动演化过程[19]其演化可分为三个阶段,(a)为滑移速率的演化,加速阶段对应了地震的成核期.(b)为对应时间段断层老化状态的演化.Fig.2 A typical seismic cycle derived from Eqs.(6),(7)and(8)[19]Slip rate(a)and fault state(b)vary with time throughout an entire seismic cycle.In Phase 1,the fault is approximated locked and slip rate is well below that of the loading point.In Phase 2,the fault slip rate increases rapidly. “Phase 3”represents the co-seismic rupture.
2.3 依赖于时间的形变过程
在给定的孕震深度内,断层的剪切失稳和滑移是由Coulomb 应力所控制的[20].Coulomb 模型可由(10)式给出:

公式(10)中,τ为滑移方向剪切应力的幅值,σ为作用于断层上的有效正应力,包括了孔隙水压.设定断层目前所处的构造背景应力场分别为τ0和σ0,来自于同震过程或其它非构造应力变化的剪应力和正应力扰动分别为Δτ和Δσ,则新的剪应力和正应力分别为τ1=τ0+Δτ和σ1=σ0+Δσ.
进一步,我们设定所有的应力扰动量Δτ≪τ0,Δσ≪σ0,由此产生的Coulomb 应力变化可写为ΔCFF=Δτ-μ0Δσ.由公式(10)可知,地震发生前,Coulomb应力可以忽略,即有ΔCFF≫τ0-μ0σ0.根据公式(6)可得:
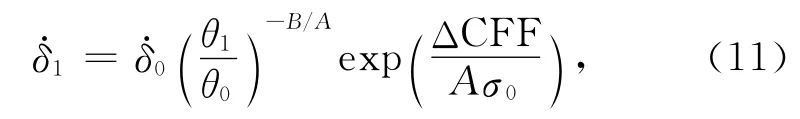

利用log(1+x)≈x(x≪1),(12)式也可写成对数形式:

或写成差分形式:


公式(14)实际上反映了断层受应力扰动时滑移速率的相对变化.ΔCFFG=Δτ-(μ0-α)Δσ可称之为广义Coulomb应力扰动.
2.4 Coulomb应力扰动下的时钟变化
在前面的讨论中,我们以单自由度弹簧-滑块模型给出了断层在远场应力加载下演化的主要三个阶段.以下我们讨论当断层处于演化的第一个阶段,受Coulomb应力扰动的作用时断层演化过程所发生的改变,即演化可发生时间上的提前或推后,进而可改变其演化状态(失稳时间的提前或推后).从图2可以清楚地看出,当断层处于演化阶段1时,滑动位移δ→0,dθ/dt≈常数.因此,θ~θ0+ct.根据公式(6)、(8)和(9)可得:
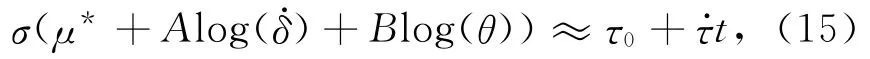
公式中μ*=μ0-Alog(δ·*)-blog(θ*).(15)式对时间求导数,有:
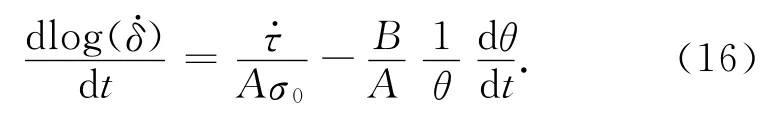
由于断层演化处于第一个阶段,时间t远远大于0,因此,公式右边第二项可以忽略.写成差分格式,由此可得:

同前面所得到的公式(14)相比较,有:

公式(18)(α=0)被广泛应用于对余震触发机制和地震影区成因的解释[11].在依赖于时间的概率地震预测研究中,公式(18)也为概率模型研究提供了十分重要的参数[5].例如,设定某一发震断层的平均回复周期为T,那么受到Coulomb应力扰动的影响,修正后的回复周期T′可变为:
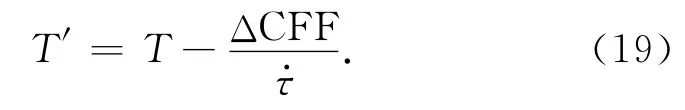
从另外一个角度来看,如果发震断层自上(前)次地震至今所经历的时间为t,那么受Coulomb应力扰动的影响,修正后的时间t′应该包括了ΔCFF造成的时间平移:
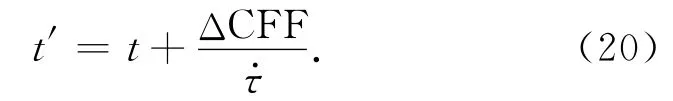
从目前的推导中,我们发现公式(18)的应用范围有较大的局限性.针对断层的远场加载给定时,我们假设了断层处于图2所示的第一阶段,即早期演化阶段.如果断层演化期已处于图2所示的成核(加速期)阶段,上述公式则会存在较大的误差和不确定因素.更为困难的问题是,对于每个断层来讲,事实上目前没有明确的方法确定断层具体处于哪个演化期.
另外一点需要指出的是,如果断层的加载过程也包含了正应力随时间的波动σ(t)=Δσ(t),地震的重复周期为T,并且≪σ0,≪σ0,那么在以上公式中的剪切应力加载率可由(21)式Coulomb应力加载率取代[21]:

3 Dieterich 余震触发理论的一般性表达式
3.1 断层群体化概念模型
在任一地震活动区内,地震发生频度同震级遵从G-R(震级-频度)关系,且地震发生服从Poisson过程.进一步,我们设定任一时间段Δti=ΔTi+1-ΔTi内地震发生的个数ni只同时间段Δti的长短相关,也就是说地震发生频度为一常数值,那么该区域内的地震活动性处于平稳状态,可定义为背景场或称之为参考场(图3a),由r来表示.

图3 应力扰动前后断层失稳时间轴变化示意图[22](a)为应力扰动前断层的失稳时间.(b)为应力扰动后断层的失稳时间.Fig.3 Schematics showing how the time to instability for each nucleation site in the population changes due to a stress step for a monotonic function f(T)[22](a)is the original time to instability and(b)is the new time to instability after the static stress step.
当该区域未受到大震同震位移所引起的静态应力场扰动时,该区域的背景场不变,即取任意的时间段计算地震在单位时间的发生个数,计算结果近似相等,于是有:

其中ni为Ti到Ti-1时间段内的地震个数(图3a).
当区域内的尺度不同的断层受到来自主震同震位移所导致区域内静态应力变化或应力扰动后,每个断层的失稳时间t发生变化,如2.4节所描述,受Coulomb应力变化所造成的时钟提前或退后(Δt≈ΔCFF/).设提前或推后量为t的 函 数,表示为f(t),那么单位时间内新的地震发生个数R可以表示为[22](图3b):

将公式(23)代入公式(22)中,则与背景场相关的余震的发生率可写为:
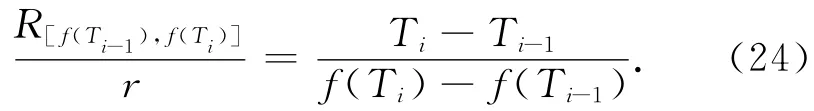
当Ti-Ti-1趋近于无限小时,其微分解为:

公式(25)中T表示背景场下地震发生时间,而f表示受到扰动后的地震发生时间.
3.2 余震触发机制的Dieterich广义解
设未经应力扰动,断层失稳时间由附录A 中公式(A6)给出.当断层受Coulomb应力扰动,由公式(11)或(12)可知,断层上的滑移速率发生了突发的变化,即从δ·0变为δ·1,由此,在新的滑移速率δ·1作用下,断层的失稳时间可改写为:
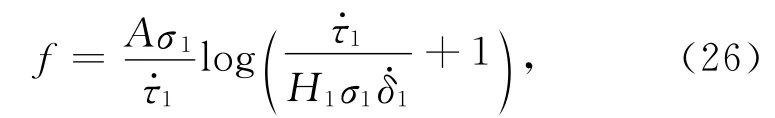
其中,H1=B/Dc-k/σ1,δ1=
图4给出了由R-S本构关系和单自由度弹簧-滑块模型,即公式(6)、(8)和附录A 中的公式(A3)求解所得到的断层滑移速率演化过程.需要注意的是,图中给出的是当应力扰动正值时发震时间提前的情形,当应力扰动小于零时,f>T造成断层发震(失稳)时间的推后.受应力扰动后断层失稳时间的提前或推后量Δt可由附录A 中公式(A6)和公式(26)求得:

图4 Coulomb应力扰动前后断层滑移速率随时间的演化特征t1 表示应力扰动的加载时刻,Δt表示应力扰动后的时钟提前量.Fig.4 Fault slip rate variation before and after Coulomb stress perturbationt1is the loading time of stress perturbation.AndΔt is a clock advance due toΔCFF applied at t1.

从图4也可看出,Δt是一个依赖于初始滑移速率和应力扰动后的滑移速率的对数函数,并同应力扰动的加载时间有关.上文中所给出的Coulomb应力扰动所得到的时间提前或推后量Δt=ΔCFF/(公式(18))无法满足对断层处于不同演化阶段的要求,事实上只有当Tτ·/Aσ≫1时[7],公式(18)才能得到很好的近似.例如,反映在公式(27)中:

如果公式(25)成立,可得R/r=dT/df=1,即受应力扰动后的地震活动性等同于背景场的地震活动性.因此,Coulomb 应力扰动(变化)模型无法预测Omori余震衰减过程,由公式(18)直接用于依赖于时间的概率地震危险性预测可能会造成过高或过低的概率取值.
由附录B 中公式(B3)和公式(25),我们得到Coulomb应力扰动后的余震发生率R:
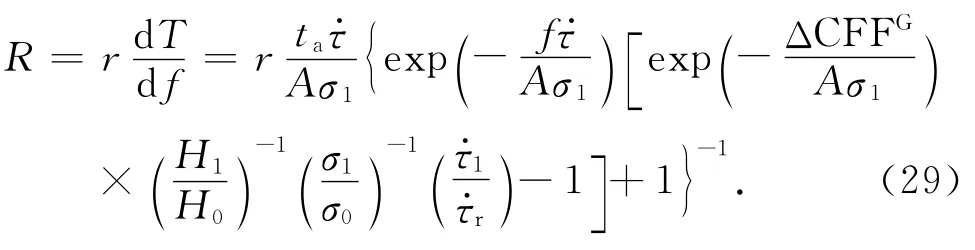
一般说来,Δσ/σ0≪1,因此,可假设σ1/σ0≈1,H1/H0≈1.将f以时间t表示,则公式(29)可以写为:
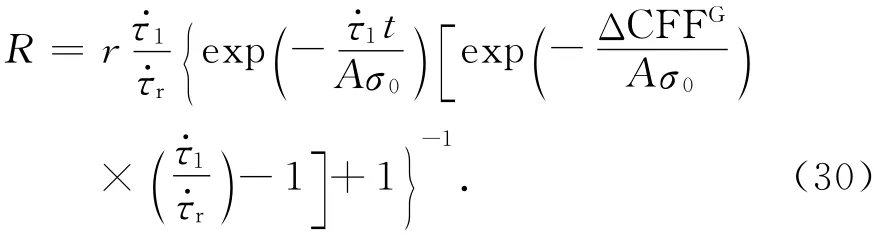
如果将τ·G=-μ0σ·代替Dieterich触发机制解(公式(30))中的r 和1,公式(30)可以改写为:
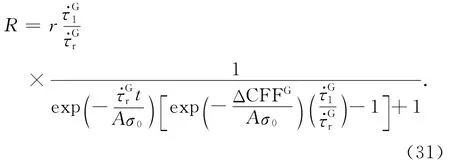
公式(30)同Dieterich[2,13]方程具有相同的形式,但导出的过程则基于直观的断层群体化概念模型.从该式中可以看出,余震的发生率不仅同广义的Coulomb应力变化ΔCFFG相关联,而且同主震前后的剪应力加载速率比值1/r有依赖关系.即使ΔCFFG为零,剪应力加载速率的变化仍可对余震地震活动性产生影响.进一步,由断层群体化概念模型(公式(23))可知,余震累计个数随时间的变化关系为:

记主震发震时刻t0=0则有:
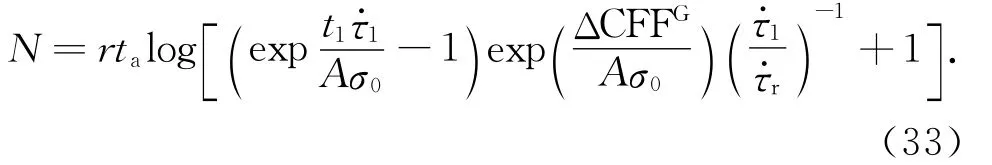
4 应用实例:唐山地震余震序列拟合
1976年7月28日MS7.8唐山大地震是20世纪发生在华北地区的重大事件,地震对唐山及其周边地区造成了重大的人员伤亡和财产损失,主震之后约15小时滦县又发生了MS7.1的地震.同年11月15日,宁河又发生了MS6.9的地震,之后有大量余震发生并一直持续至今,使得该区域一直保持了同主震前相比较高的地震活动性.
图5a为唐山及其周边地区的地形、活动断层和1976年7月28日MS7.8唐山地震前的历史地震,图5b为唐山地震后至今的地震活动.图中圆点表示历史地震活动,实线为断层,方块标记主要城市位置.图5c为M-T图(震级-时间图),对应于图左的纵坐标;曲线为地震年发生率随时间的变化,对应于图右边的对数坐标.唐山地震发生于地震较为活跃的华北盆地北缘.唐山断层为一隐伏断层,震后地表主破裂带长达8km,总体走向N30°E[23].主震震源深度 约 为15 km,断层宽度为20 km[24].Butler等[25]在对唐山地震震源机制的研究中给出唐山地震主震为MS7.7级,唐山断裂的长度约为140km,地震矩M0=1.8×1020N·m,主震静态应力降为30×105Pa[25];Huang 和Yeh[24]给出唐山地震主震为MS7.8级,断层长度为48km,地震矩M0=9.8×1019N·m,主震静态应力降Δτe=(45±5.5)×105Pa[24].唐山地震主震平均滑动位移为3.53m[24].另外,活动构造分析表明唐山断裂带上7级以上地震的重复周期约为3000~4000年[26].静态库仑应力模型结果也表明,唐山地震主震最大库仑应力ΔCFF 变化约为2×105Pa[27-28].

图5 (a)为唐山及其周边地区的地形、活动断层和震级MS≥2.0的1 976年7月28日MS7.8唐山地震前的历史地震,(b)为唐山地震后至今的地震活动.图中圆点表示历史地震活动,实线为断层,方块标记主要城市位置.(c)中火柴棒图显示了该区域的各个地震的震级和发震时间,对应于图左的纵坐标;曲线为地震年发生率随时间的变化,对应于图右边的对数坐标.Fig.5 (a)and(b)show the regional seismic events before and after the 1976,MS7.8,Tangshan earthquake,respectively.The active faults are indicated by solid lines,and the solid circles represent MS≥2.0seismic events,and the squares show the locations of major cities.(c)gives M -Tplot of aftershock occurrence after mainshock,and the solid curve describes the earthquake annual rate varies with time.
以唐山地震的主余震序列为例,利用公式(31)和(33),我们对唐山地震主震后的余震发生频度和累计个数进行拟合.在对余震随时间衰减过程的拟合中(图6),我们发现,如果地震前后区域剪应力速率保持不变,即采用1=r,当ΔCFF 值从(1~4)×105Pa时,拟合曲线同实际数据之间总存在一定的差异.实际余震个数随时间增加而显示出的波动性也表明震后区域应力场随时间的变化可能影响到余震的触发.尤其早期的余震个数受区域应力场的改变更大.

图6 1976年MS7.8唐山地震后余震年发生率随时间的变化图中方块为由实际地震目录得到的M≥2.0的地震年发生率.三条曲线均为应用公式(30)由背景场地震计算得到的M≥2.0的地震年发生率.在计算中,取Aσ=1,ta=85年,虚线、实线和点划线分别对应Δτ~0.4,0.2,0.1 MPa.Fig.6 Number of aftershocks due to the 1976 MS7.8 Tangshan earthquake varies with timeSolid squares are the recorded annual number of aftershocks with M≥2.0.With a given background seismicity rate r0(M≥2.0),the dashed,solid and dot-dashed lines are derived from Eq.(30)corresponding toΔτ=0.4,0.2and 0.1MPa,respectively,when ta=85and Aσ=1.
因此,为了获取最佳拟合过程,我们对公式(31)和(33)进行了改正,对余震发生率或累计个数的计算采用了分段拟合.其主要思路来源于近期GPS观测成果[29],即主震后断层上的滑移并未完全停止,震后蠕动或震后滑移仍然在进行中,从而导致应力场的进一步调整.受此影响,主震后的一段时间内具体地讲,分段计算的主要思路来自Segall等[30]对火山地震活动性的研究.记主震时刻为t0,当t0<t<t1时,受同震位移及震后位移和应力松
弛过程的影响,断层上的剪应力变化率远大于背景场剪应力变化率,(t0<t<t1)≫r.剪应力的变化在第一阶段已经完成,即Δτ=(t1-t0).当t>t1时,断层上的剪应力变化率则回到背景场,(t>t1)=r.因此,对公式(31)和(33)的分段可简化为:
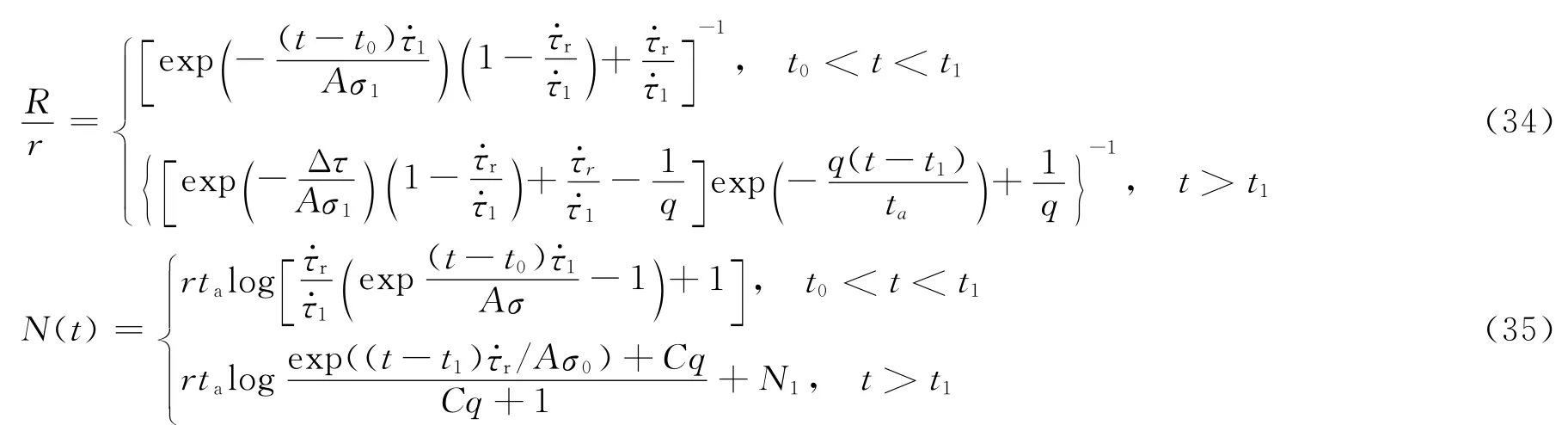
当已知余震的持续时间和背景场地震个数时,拟合曲线和实际地震数据的相关性,很大程度上取决于Δτ值.Δτ=(t1-t0)1 是断层失稳瞬间的剪应力变化量.图7a为Δτ=13×105Pa时,MS≥3.0唐山地震余震序列的拟合.图7b 为地震发生若干天内,t1取不同值时,对余震序列的拟合.图7b中的结果也说明了断层失稳时应力降的变化是在数分钟至几小时内完成的.在以上余震序列的拟合中,我们选取Aσ=1,余震持续时间ta=85年[31].在图7a的拟合中q=1,而在图7b的拟合中q=1.05,即断层失稳后短时间内,剪应力变化率瞬间增大,这段时间内产生的剪应力降影响其后的余震个数,此后剪应力的变化率仅在地震后的数天内略大于背景场剪应力变化率,并很快恢复到.
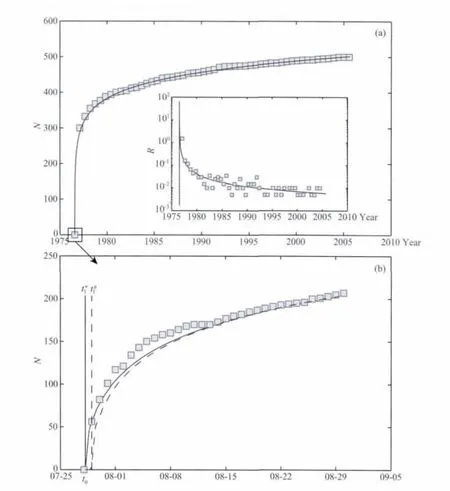
图7 唐山地震后的地震序列随时间变化关系拟合(a)为对唐山地震后至2005年内,MS≥3.0的地震序列的拟合,方块为实际地震序列,实线为公式拟合出的地震序列;(b)为唐山地震后5个月内的地震序列拟合,方块为实际地震序列,实曲线为以t*1 时刻分段计算得到,虚曲线为以t#1 时刻分段计算得到.Fig.7 Cumulative number of aftershock sequences varies with time from the 1976 MS7.8Tangshan mainshock(a)gives the fitting results for MS≥3.0earthquake sequence between 1976and 2005.(b)is the fitting result from earthquake sequence within first 5months.Squares represent the annual number of earthquake events obtained from published earthquake catalogs.Solid and the dotted curves correspond to the different t1used in Eq.(35),respectively.
5 讨论与结论
Dieterich[2]余震触发理论认为主震引起的断层上的剪应力变化,导致了区域内地震活动性的改变.在该理论的深入研究和应用中,Dieterich[13]给出了修正解,以Coulomb 应力的变化取代了剪应力变化.但并未给出明确的阐述.需要强调的是,Dieterich理论模型已广泛应用于现代依赖时间的概率地震预测中[6,11-12],因此,通过必要的理论探讨,深入了解其物理含义,有助于该方面研究的深入和成果应用的推广.本文从直观简单的群体化理论概念出发,给出了Coulomb应力作用下Dieterich余震触发机制的广义解,其方程的结构和形式同Dieterich[2,13]理论解.需要注意的是,群体化理论模型仅用单位时间内发生的地震个数,而并未区分不同震级(能量)的地震个数.与地震矩相关的积累Benioff应变,已应用于地震预测[32]和强震复发周期的研究中[33-34].然而,断层受到应力扰动,导致发震时钟提前/推后时,其积累Benioff应变是否与未受应力扰动时相同,有待深入的研究和讨论.基于R-S关系和单自由度弹簧-滑块模型,本文也重点讨论了Coulomb应力变化/扰动模型的优点和存在的局限性,并指出了可能的解决方案.由此产生的对Coulomb应力变化/扰动模型中发震时间的Δt=ΔCFF/新认识,可为依赖时间的概率地震预测模型的建立提供新的参考依据.利用本文所得到的结果,我们对1976年唐山地震的余震序列进行了拟合.为了获取最佳拟合结果,对余震发生率R(t)和累计个数N(t)的计算采用了视时窗分段方法[30].拟合结果也反映了由震后滑移、应力松弛等造成的区域构造应力场的短时期改变应该是早期高余震发生率的一个主要原因,而主震断层内部的静态应力降应该是在瞬间完成的.
附录A Dieterich余震触发机制
正文中公式(7)给出了状态变量θ随时间的演化方程.如果考虑到≈0,则公式(7)可写为:

所对应的积分解为:

如果采用/Dc≫1,则积分解可写为:
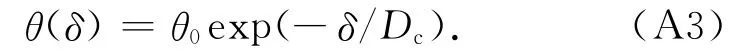
结合文中公式(2)、(6)和公式(A3),当≠0时,断层面上的滑动位移和滑动速率分别为[16]:

其中H=B/Dc-k/σ.断层若发生失稳则意味着滑移速率突然增加,远远大于对断层的加载速率,在此我们令→+∞,则上述公式中所对应的时间尺度t即为断层的失稳时间:
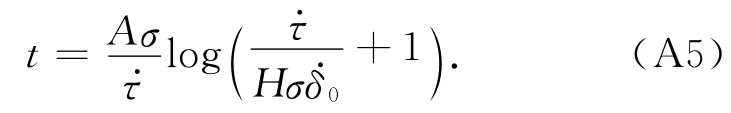

其中,H0=B/Dc-k/σ0.
附录B 分段求解余震序列
将公式(12)代入公式(26)并做一些必要的整理,得到:

进一步,将公式(A6)代入公式(B1),经过必要的代数运算,可以得到应力扰动前后T与f的函数关系:
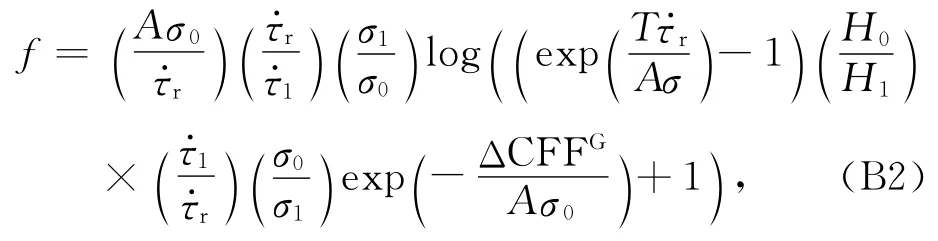
(B2)式也可改写成:

其中,ta=Aσ0/r表示余震持续的特征时间.
假设剪应力变化率为一个阶梯函数:t0<t<t1时,剪应力变化率为,且t=t0时ΔCFF =0、Δτ=0、Δσ=0;当t>t1时,剪应力变化率回到接近于的值,定义其值为2=r,q≈1.则

根据t=t1时余震序列的连续性有R|t1+=R|t1-:

代入公式(B4)有:

当q=1,即时,回到Segall等[30]给出的公式:
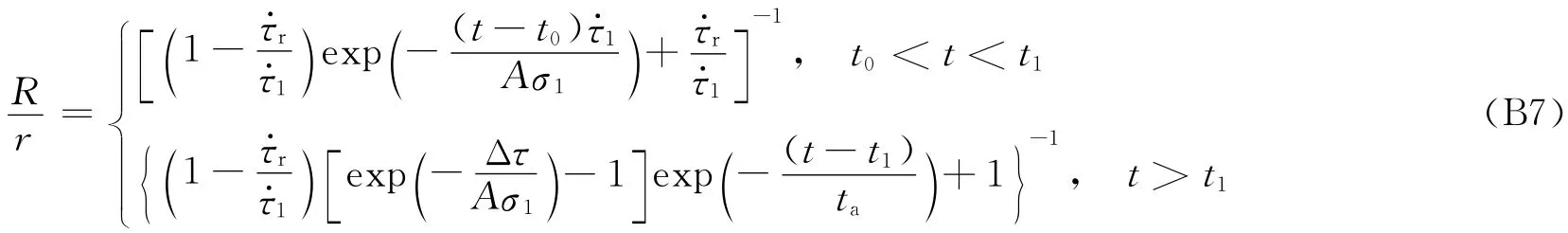
当t1→t0时有:

即为Dieterich[2]文章中的公式[12].
(References)
[1] Freed A M.Earthquake triggering by static,dynamic,and postseismic stress transfer.Annu.Rev.EarthPlanet.Sci.,2005,33(1):335-367.
[2] Dieterich J.A constitutive law for rate of earthquake production and its application to earthquake clustering.J.Geophys.Res.,1994,99(B2):2601-2601.
[3] King G C P,Stein R S,Lin J.Static stress changes and the triggering of earthquakes.Bull.Seismol.Soc.Amer.,1994,84(3):935-953.
[4] Harris R A,Simpson R W.Changes in static stress on southern California faults after the 1992Landers earthquake.J.Geophys.Res.,1992,103(B10):24439-24451.
[5] Stein R S,Barka A A,Dieterich J H.Progressive failure on the North Anatolian fault since 1939by earthquake stress triggering.Geophys.J.Int.,1997,128(3):594-604.
[6] Parsons T,Toda S,Stein R S,et al.Heightened odds of large earthquakes near Istanbul: an interaction-based probability calculation.Science,2000,288(5466):661-665.
[7] Hardebeck J L.Stress triggering and earthquake probability estimates.J.Geophys.Res.,2004,109(B4):B04310,doi:10.1029/2003JB002437.
[8] Parsons T.Significance of stress transfer in time-dependent earthquake probability calculations.J.Geophys.Res.,2005,110(B5):B05S02,doi:10.1029/2004JB003190.
[9] Gomberg J,Belardinelli M,Cocco M,et al.Time-dependent earthquake probabilities.J.Geophys.Res.,2005,110(B5):B05S04,doi:10.1029/2004JB003405.
[10] Working Group on California Earthquake Probabilities.Probabilities of large earthquakes in the San Francisco Bay region.Calitbmia,U.S.Geol.Surv.Circ.1053,1990.
[11] Harris R A.Introduction to special section:Stress triggers,stress shadows,and implications for seismic hazard.J.Geophys.Res.,1998,103(B10):24347-24358.
[12] Toda S,Stein R S,Reasenberg P A,et al.Stress transferred by the 1995Mw=6.9Kobe,Japan,shock-Effect on aftershocks and future earthquake probabilities.J.Geophys.Res.,1998,103(B10):24543-24565.
[13] Dieterich J H,Kilgore B.Implications of fault constitutive properties for earthquake prediction.Proceedingsofthe NationalAcademyofSciences,1996,93(9):3787-3794.
[14] Ruina A.Slip instability and state variable friction laws.J.Geophys.Res.,1983,88(B12):359-310.
[15] Dieterich J H.Modeling of rock friction 1.Experimental results and constitutive equations.J.Geophys.Res.,1979,84(B5):2161-2168.
[16] Dieterich J H.Earthquake nucleation on faults with rate-and state-dependent strength.Tectonophysics,1992,211(1-4):115-134.
[17] Dieterich J H.A model for the nucleation of earthquake slip.EarthquakeSourceMechanics,1986,37:37-47.
[18] Scholz C H.Earthquakes and friction laws.Nature,1998,391(6662):37-42.
[19] Ziv A,Rubin A.Implications of rate-and-state friction for properties of aftershock sequence:Quasi-static inherently discrete simulations.J.Geophys.Res.,2003,108(B1),doi:10.1029/2001JB001219.
[20] Byerlee J.Friction of rocks.PureAppl.Geophys.,1978,116(4-5):615-626.
[21] Perfettini H,Avouac J.Postseismic relaxation driven by brittle creep:A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks,application to the Chi-Chi earthquake,Taiwan.J.Geophys.Res.,2004,109(B2),doi:10.1029/2003JB002488.
[22] Kaneko Y.Investigations of earthquake source processes based on fault models with variable friction rheology[Ph.D.thesis].California:California Institute of Technology,2009.
[23] 尤惠川,徐锡伟,吴建平等.唐山地震深浅构造关系研究.地震地质,2002,24(4):571-582.
You H C,Xu X W,Wu J P,et al.Study on the relationship between shallow and deep structures in the 1976 Tangshan earthquake area.SeismologyandGeology(in Chinese),2002,24(4):571-582.
[24] Huang B S,Yeh Y T.The fault ruptures of the 1976 Tangshan earthquake sequence inferred from coseismic crustal deformation.Bull.Seismol.Soc.Amer.,1997,87(4):1046-1057.
[25] Butler R,Stewart G S,Kanamori H.The July 27,1976 Tangshan, China earthquake-A complex sequence of intraplate events.Bull.Seismol.Soc.Amer.,1979,69(1):207-220.
[26] 邓起东,徐锡伟,于贵华.中国大陆活动断裂的分区特征及其成因.∥中国活动断层研究.北京:地震出版社,1994:1-14.
Deng Q D, Xu X W, Yu G H. Characteristics of regionalization of active faults in China and their genesis(in Chinese).∥China Active Faults Reserch.Beijing:Seismological Press,1994:1-14.
[27] Robinson R, Zhou S. Stress interactions within the Tangshan,China,earthquake sequence of 1976.Bull.Seismol.Soc.Amer.,2005,95(6):2501-2505.
[28] 万永革,沈正康,曾跃华等.唐山地震序列应力触发的粘弹性力学模型研究.地震学报,2008,30(6):581-593.
Wan Y G,Shen Z K,Zeng Y H,et al.Study on visco-elastic stress triggering model of the 1976 Tangshan earthquake sequence.ActaSeismologicaSinica(in Chinese),2008,30(6):581-593.
[29] Cui X F,Xie F R,Zhang H Y.Recent tectonic stress field zoning in Sichuan-Yunnan region and its dynamic interest.ActaSeismologicaSinica,2006,19(5):485-496.
[30] Segall P,Desmarais E K,Shelly D,et al.Earthquakes triggered by silent slip events on Kilauea volcano,Hawaii.Nature,2006,442(7098):71-74.
[31] 仲秋,史保平.1976年Ms7.8唐山地震余震序列持续时间及对地震危险性分析的意义.地震学报,2012,34(4):494-508.
Zhong Q,Shi B P.Aftershock time duration of the 1976Ms7.8 Tangshan earthquake and implication for seismic hazard.ActaSeismologicaSinica(in Chinese),2012,34(4):494-508.
[32] 秦四清,徐锡伟,胡平等.孕震断层的多锁固段脆性破裂机制与地震预测新方法的探索.地球物理学报,2010,53(4):1001-1014,doi:10.3969/j.issn.0001-5733.2010.04.025.
Qin S Q,Xu X W,Hu P,et al.Brittle failure mechanism of multiple locked patches in a seismogenic fault system and exploration on a new way for earthquake prediction.Chinese J.Geophys.(in Chinese),2010,53(4):1001-1014,doi:10.3969/j.issn.0001-5733.2010.04.025.
[33] Steven C J,Lynn R S.Evolving towards a critical point:a review of accelerating seismic moment/energy release prior to large and great Earthquakes.PureAppl.Geophys.,1999,155(4):279-306.
[34] 蒋长胜,赵祎喆,王行舟.亚洲地区Benioff应变释放和强震活动的周期性特征研究.地震,2010,30(3):72-80.
Jiang C S,Zhao Y Z,Wang X Z.Benioff strain release and periodic characteristics of strong earthquake activities in Asia.Earthquake(in Chinese),2010,30(3):72-80.

