水下图像的噪声滤波与仿真

淦元柳，李富栋

(空军驻锦州地区军事代表室，辽宁锦州121000)

1 引言

图像噪声是混淆在有用信号里的干扰信号，待处理的图像中一般都包含不同程度的噪声。图像噪声多数情况是随机产生的，因此具有分布和强度不规律的特点。这些噪声对以后的处理过程产生影响，致使图像失真，所以为了使图像被恢复到尽可能的接近真实，去噪处理对图像预处理而言就显得尤为重要。为此，本文就水下图像噪声滤波方法、Nonlocalmeans算法、仿真试验等，作了进一步的研究和探讨［1］。

2 图像噪声滤波

水下图像噪声滤波方法主要采用均值滤波和中值滤波［2］。

(1)均值滤波。均值滤波是用均值代替原图像中的各个像素值，是一种直接的空间域滤波方法。首先是选择一个模板，然后对待处理图像的当前像素套用这个模板，该模板覆盖其邻近的若干像素，对模板中的所有像素取均值，代替原像素值。

例如，设噪声η(m，n)是高斯白噪声，令其方差为σ2，均值为0，该噪声与图像f(x，y)没有相关性。加性噪声的图像f'(x，y)为:

经邻域平均法处理以后的图像g(m，n)为:

式中，S是(m，n)点的邻域内的点集，图1是这种点集的例子。

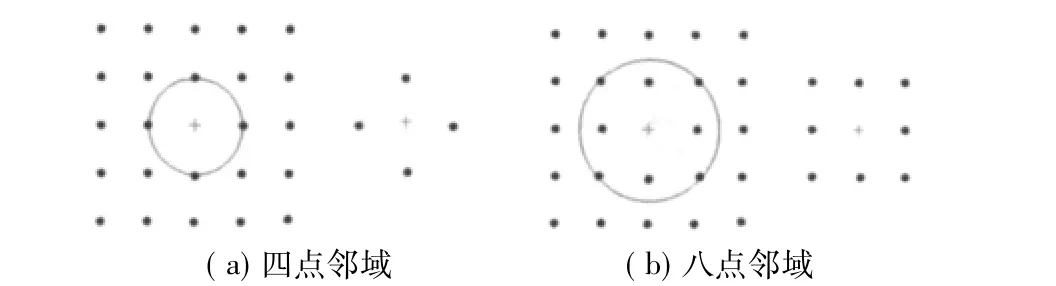
图1 (m，n)点的两种邻域

可以看到，应用邻域滤波方法之后，剩余噪声的平均值仍然为0，而方差却从原来的 σ2减小为但是线性滤波器导致了图像g(m，n)失真，表现在图像中即为目标物体的边缘或者局部特征变模糊了，但这并不影响后期处理中对目标形状的识别，而且由于该算法思路简单易于操作，计算量小，在对处理效果要求不很苛刻的条件下，邻域平均方法也是行得通的。邻域均值滤波的应用实例如图2所示。

图2中的图像为水下图像，主要包括正方体、三棱锥、球体、椭球体四种待处理的目标，为8 bits灰度图像，图像大小为720×576。

由图2可以看出经过邻域均值滤波后水下图的像噪声得到了抑制，但同时对目标的边缘带来了负面的影响，使得局部特征变模糊，虽然对于水下图像来说，这不影响最终识别结果，但是考虑到识别精准度，还需要开展进一步研究工作。

邻域M的大小决定了滤波的程度，邻域尺度越大滤波程度就相应加大，大尺度滤波器导致的图像细节的损失就是作为去除大噪声的代价。均值滤波去除噪声的效果虽然非常明显，但图像边缘变得模糊，这是由图像边缘处的信息被处理的也趋于均匀造成的。为了进一步改进这种算法，取闭值的均值滤波和加权均值滤波被人们提了出来，但是这些方法也在一定程度上改善了边缘模糊效应，并没有完全彻底的解决这个模糊的问题。

(2)中值滤波。中值滤波(Medianfilter)是基于排序统计理论的一种非线性去噪方法，该种滤波方法能够在一定范围内有效的抑制非线性噪声。中值滤波的优点是运算简便、编程方便、速度相对较快。在对应的映射函数选择时，采用非线性方法，能尽最大限度的保持原有图像的有用信息，从而有效地剔除脉冲干扰及图像扫描噪声。

·中值输出。假设一个数组 x1，x2，…，xn，把这n个数值按照大小顺序排列起来:

那么y称为序列x1，x2，…，xn的中值，若有一个序列为{0，3，4，1，7}，排序后的序列为{0，1，3，4，7}，则 Med{0，1，3，4，7}=3 就是它的中值输出。

·窗口。一维的情形比较简单，映射范围是一个有奇数个点的滑动窗口(长度一般取奇数)，接下来用窗口内数组序列的中值去代替窗口中心点的数值。

设有一个一维序列{xi，i∈I}，其中，I取值范围为自然数集合(或其子集)，取2k+1为窗口长度(点数)，进行中值滤波运算就是在这个一维序列中抽出 2k+1 个数值 xi－k，…，xi，…，xi+k，其中 xi为该窗口的中心点数值，取完之后再把这2k+1个点按其数值大小进行排序，滤波器输出则是序号为中心点的那个数值:

如图3所示，它是一维情况应用不同的滤波方法的结果比较的一个示例，在这里中值窗口被取为含有5个元素，可以看到不同的方法应用后结果输出的差别。从图3中还可以看出，阶跃函数和斜坡函数在一维情况下并不受到中值滤波器的影响，单、双脉冲被效地消除，三角函数的顶端也变的平坦很多。

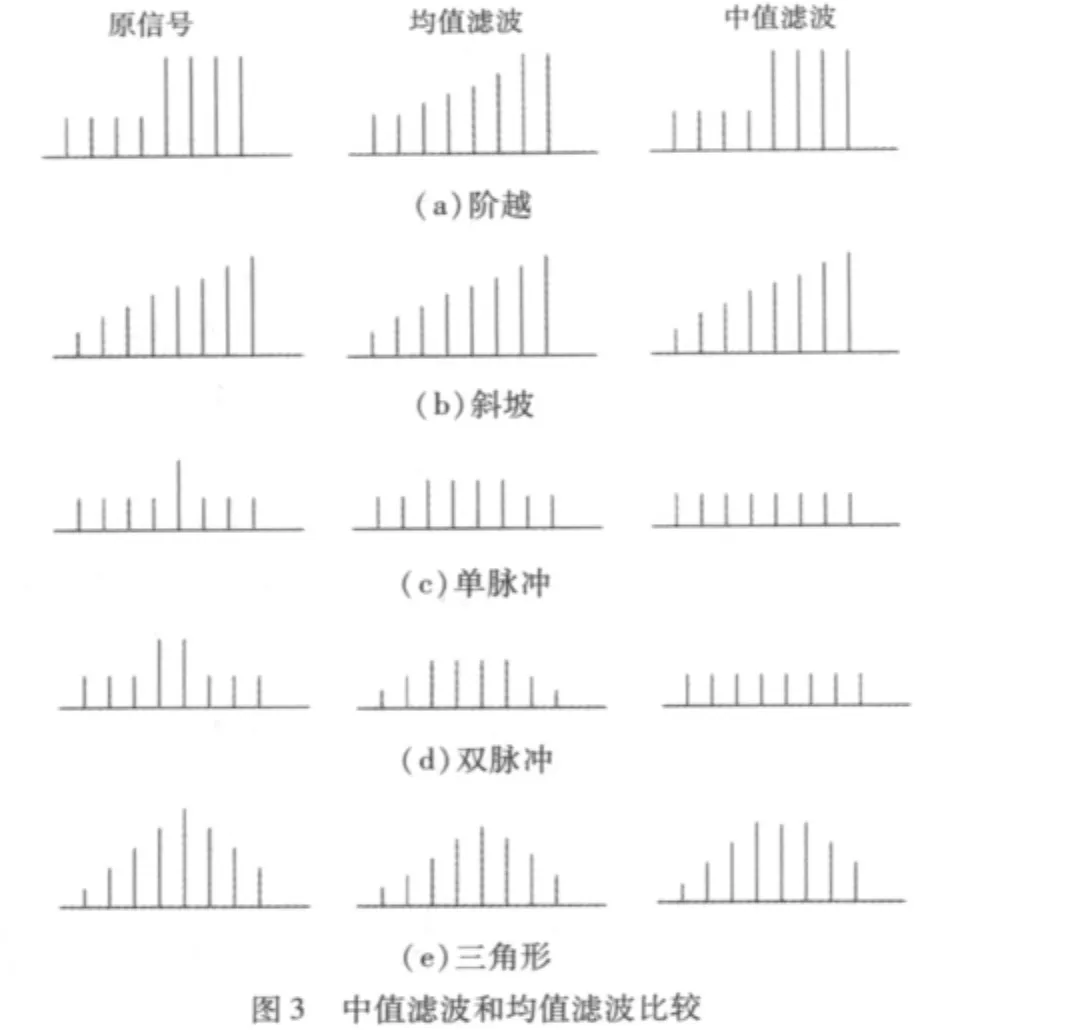
把一维的定义推广一下，就得到了二维的中值滤波的概念，这个时候把窗口也扩展为二维。把数字图像各点的灰度值表示为二维数组{xi，j(i，j)∈I2}，那么滤波窗口为A的二维中值滤波定义可以描述为:

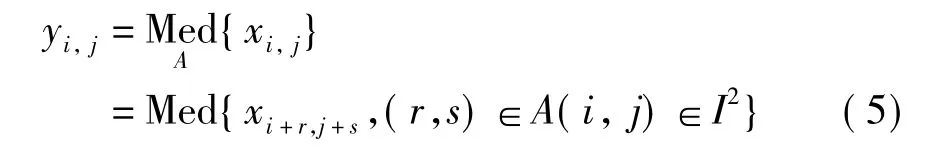
·窗口的选用。针对实际问题，为了处理不同的图像，通常选用不同形状和尺寸的窗口。线形、矩形、圆形、梯形及圆环形等都能够被作为二维中值滤波运算的窗口形状，尺寸一般先用3再取5逐点增大，窗口的中心点被置于待处理点的位置上，通过这样的窗口函数，逐点进行滤波处理，最后输出结果。一般情况下，何种形状的窗口适用于何种类型的图像，方形或者圆形窗口适用于缓变的较长轮廓线物体的图像，十字形窗口适用于含有尖顶角物体的图像，图像中有用信息的尺寸应大于窗口的尺寸。

·根信号特性。中值滤波根信号特性是指图像经过中值滤波处理后，其信号成分仍保持不变。大量的研究表明，在有限次中值滤波处理后一维信号仍旧能够收敛为根信号。另外，中值滤波对于脉冲噪声消除和高斯噪声平滑的能力没有中值滤波根信号性能表现得优良。

中值滤波的效果如图4和图5所示。图4为各种形状图像原图，图5即为对某一形状图像进行7×7中值滤波用来去除图中噪点、细线等噪声以达到目标增强的实例。

从图5可以看出点、线状噪声对于中值滤波较为敏感，而且目标区域轮廓几乎不受影响，因此该方法较适用于水下图像的滤波，此外，考虑到图像成像时成像设备本身的非线性失衡的影响需要进行校正，在进行滤波前也可考虑引入非线性点运算，来强化部分灰度区域信息。

3 Non-localmeans算法

Non-localmeans算法是一个性能优良的空域滤波方法。假设图像加噪声的信息集合为ν={ν(x)/x∈I}，用NL方法滤波之后的图像设为 NL［ν］(x)，针对每一个像素x，那么通过用加权平均的方法计算之后得到去除噪声之后的图像表达式［3］:

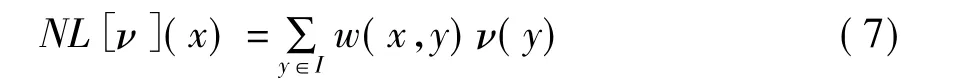
式中，w(x，y)是权值，根据像素点x和像素点y之间的相似程度来计算，并且满足0≤w(x，y)≤1，∑yw(x，y)=1。

通过上述描述可以看出，简单的对两个像素点进行直接差值运算所得到的结果并不能准确的度量其相似程度，而是通过求得权值的方法来比较两个区域ν(Nx)和ν(Ny)的相似程度。令ν(Nk)表示以像素k为中心的一个矩形区域，那么利用这个矩形区域内的对应像素相减之后的平方和的大小用来度量这两个像素之间的相似程度，所求得的平方和越大，说明两个像素的相似程度越小，反之，当求出的平方和的值越小，说明两个像素之间的差别就越小，也就是说像素的相似程度就越高。

如图6所示，待处理的像素点是图中所标出的实线区域的中心点A，参考的准备加权平均的像素点是在它的邻域的点B，也就是虚线部分的中心像素点，把这两个区域(A点为中心的3×3的矩形窗口和B点为中心的3×3矩形窗口)对应的像素点的灰度值进行相减后求平方和，即(1－1')2+(2－2')2…来度量权值，按照式(8)计算权值:

其中，Z(x)是用来归一化的:

图6 对应像素示意图

图7 Non-localmeans算法实验结果

4 仿真试验

以水下球体图像为例给出Non-localmeans算法的仿真结果［4］，实验中，图像大小为搜索区大小为5×5，匹配区域大小为2×2，h=10。

以图8中的加噪图像图像为例，给出本文论述的Non-localmeans算法的PSNR结果。同时，为便于比较结果，图8、图9也分别给出了中值滤波和均值滤波算法的PSNR结果。

图8 中值滤波结果

图9 均值滤波结果

滤波算法对比结果如表1所示。从表中可以看出，这时中值滤波和均值滤波都无法得到较好结果，而采用Non-localmeans算法的结果比较理想，信噪比提高了10 dB。

表1 滤波算法对比结果

5 结束语

对于水下图像预处理的滤波中，采用Non-local means算法，其效果很好，在保持图像边缘的同时，较大程度的剔除了噪声，适合于水下颗粒噪声较明显的图像预处理。通过与中值滤波、均值滤波等常用算法对比，也证明了这一点，较大的提高了信噪比［5］。

［1］ JiangLihui，Guo Yanying．Speckle noise suppression based on an adaptive weighted morphological filter［J］．Laser ＆Infrared，2006，36(2):158 －160．(in Chinese)蒋立辉，郭艳颖．基于自适应形态滤波算法的斑点噪声抑制［J］．激光与红外，2006，36(2):158 －160．

［2］ Lan Guoning，LI Jian，Ji Fang．Underwater image backscatter noise reduction based on wavelets［J］．Ocean Technology，2010，(2):43 －47．(in Chinese)蓝国宁，李建，籍芳．基于小波的水下图像后向散射噪声去除［J］．海洋技术，2010，(2):43 －47．

［3］ Li Xin，TangWeiqiang，Li Junfeng．Study on adaptive filter based on the modulation in the laser non-destructive testing［J］．Laser ＆ Infrared，2008，38(5):498 － 501．(in Chinese)李欣，唐伟强，黎俊峰．激光无损检测中基于调制度的图像自适应滤波研究［J］．激光与红外，2008，38(5):498－501．

［4］ Chen Dong，Li Bia，Wang Weihua，et al．Research on the algorithm of suppressing speckle noise on SAR images［J］．Infrared and Laser Engineering，2000，29(4):9 －12．(in Chinese)陈东，李飚，王炜华，等．SAR图像斑点噪声消除算法的研究［J］．红外与激光工程，2000，29(4):9 －12．

［5］ Lu Guochun，Nie Wu，Zhang He．Underwater image restoration based on simulation method［J］．Journal of Dalian Maritime University，2011，(3):70 － 72，76．(in Chinese)鲁国春，聂武，张赫．基于模拟方法的水下图像复原［J］．大连海事大学学报，2011，(3):70 －72，76．