五轴车铣复合加工中心工作空间研究

高丽萍，高建设，，杨伟伟，刘德平

(1.安阳鑫盛机床股份有限公司，河南安阳455000;2.郑州大学机械工程学院，河南郑州450001)

对于一般的机械系统，应从系统工程学及工程价值学的观点去解决该系统机电及其他物理参数的协调和匹配的分析与综合问题。研究这种分析与综合的方法和理论就导致了机电一体化学科的形成和发展。机器人系统就是一个极其典型的机电一体化系统，机器人运动学及动力学则为这种系统的机电一体化的分析与综合提供必要的预备理论知识［1］。作者将机器人运动学的研究方法运用到加工中心中去。

机器人的运动学方程是表示机器人操作机或机械手每个杆件在空间相对于绝对坐标系或相对于机器人机座坐标系的位置及方向的方程［2］。对于加工中心来说，就是把具有相对运动的各个部件看成杆件，用方程来表示铣头刀尖点相对于机床坐标系的位置和方向。

1 加工中心运动学方程的建立

根据五轴加工中心的结构特点 (如图1所示)，建立D-H坐标系 (如图2所示)，求解加工中心的运动学参数。图中，{M}为机床坐标系，{W}为旋转工作台坐标系，{T}为刀具坐标系，xiyizi为中间坐标系，i=1，2，3，4。

图1 五轴车铣复合加工中心

图2 五轴车铣复合加工中心D-H坐标系

D-H变换矩阵［2］为:

设刀尖点在刀具坐标系{T}中的坐标为:

设刀尖点在旋转工作台坐标系 {W}中的坐标为:

由坐标系尺寸链可得:

故运动学方程为:

2 加工中心运动学方程的求解

(1)运动学方程的正解［3］

当加工中心操作机构的结构参数已确定，并给出各运动关节的运动参数，就可确定加工中心末端执行器在机座坐标系中所处的位置和姿态，这就是求解加工中心运动学的正问题，也称直接位置求解。

运动学正问题的求解方法是利用其运动学方程进行坐标系的连续变换，即变换矩阵的连乘，计算出矩阵中每个元素的值，它们就表示了在指定的参考坐标系中，加工中心末端执行器的位置和姿态。矩阵是唯一的，因此在驱动装置作用下操作机动作时，就给定了一组结构参数和运动参数，加工中心运动学方程的正解也是唯一的。

(2)运动学方程的逆解［3］

当加工中心末端执行器的位置和姿态给定时，如何求出各关节变量，这就是求解加工中心运动学的逆问题，也称间接位置求解。根据式 (6)两端矩阵元素应相等的原理，可得一组多变量的三角函数方程。求解这些运动参数，需解一组非线性超越函数方程。求解方法有3种:代数法、几何法和数值解法。前两类方法是基于给出封闭解，它们适用于存在封闭逆解的加工中心。关于加工中心是否存在封闭逆解，对一般具有3～6个关节的加工中心，有以下充分条件:①有3个相邻关节轴交于一点;②有3个相邻关节轴相互平行。只要满足上述一个条件，就存在封闭逆解。如CX五轴车铣复合加工中心就满足第二个条件。数值法由于只给出数值，无需满足上述条件，是一种通用的逆问题求解方法，但计算工作量大，目前尚难满足实时控制的要求。

下面介绍代数法中的递推逆变换法。

将一组逆矩阵连续左乘式 (6)两端，可得若干矩阵方程，每个矩阵有12个方程式;在这些关系式中可选择只包含一个或不多于两个待求运动参数的关系式，然后递推求解，一般递推过程不一定全部作完，就可利用等式两端矩阵中所包含对应元素相等的关系式，求得所需全部待求运动参数。

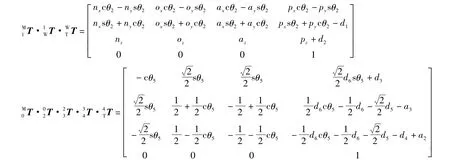
等式两边对应元素分别相等，即:

进而得出:

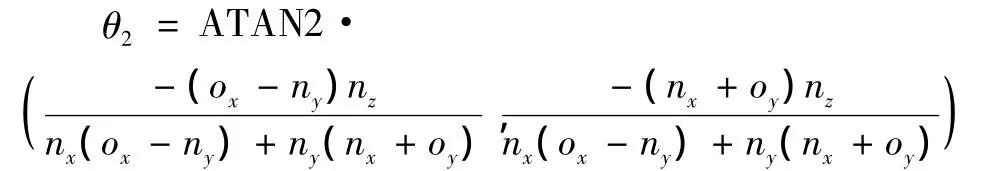
矩阵的最后一列对应元素相等，又已知 d2=得出:

3 加工中心的工作空间

加工中心工作空间代表了加工中心的活动范围，它是衡量加工中心工作能力的一个重要运动学指标。加工中心的工作空间定义为:加工中心正常运行时，末端执行器坐标系的原点能在空间活动的最大范围。这一空间又称可达工作空间［4］。目前求解工作空间的方法有很多，这里分别运用蒙特卡洛法和极限边界数值搜索法来求解，具体方法如下:

(1)蒙特卡洛法。各关节变量在各自范围内随机取值，代入运动学方程求出运动学正解，即得到末端三维坐标。

(2)极限边界数值搜索法，也称穷举法。首先求解运动学逆解，然后在一定的范围内取样，通过运动学逆解来确定各运动学参数，再根据约束条件来判断是否在工作空间之内，由此搜索符合条件的点即构成工作空间。

首先运用蒙特卡洛法，具体方法为让各运动参数在各自范围内按照一定步长取值，然后求得相应的运动方程的正解，也就得到了加工中心末端点的三维坐标值，将这些点用图形表示出来即可得到加工中心的工作空间［5］，如图3、图4所示。

图3 加工中心工作空间云图(蒙特卡洛法)

图4 加工中心工作空间截面云图(蒙特卡洛法)

然后运用极限边界数值搜索法求取加工中心工作空间，加工中心运动学方程的逆解在上一节中已经给出，在加工中心所能达到的最大范围内 (x∈［-1 300，1 300］，y∈ ［-1 300，1 300］，z∈［-100，800］)取样，通过运动学逆解来确定各运动学参数，再根据约束条件来判断是否在工作空间之内，符合条件的点构成工作空间的点云，如图5、图6所示。

图5 加工中心工作空间云图(极限边界数值搜索法)

图6 加工中心工作空间截面云图(极限边界数值搜索法)

对比两种方法所得到的加工中心工作空间点云图，可以看出:两种方法所得到的图形吻合得很好，证明工作空间的求解是正确的。

4 结论

建立了五轴加工中心的运动学方程，分析了运动学方程的正逆解。基于正逆解，分别利用蒙特卡罗法和穷举法求出加工中心的工作空间，利用MATLAB编程得出加工中心工作空间云图。对比两种方法的结果，图形吻合得很好，证明了结果的正确性，由此可知五轴加工中心的工作空间为近似的八面圆柱体。加工中心的工作空间结构紧凑，没有空腔和空洞，证明加工中心有较强的灵活性和加工能力。

【1】谢存禧，张铁.机器人技术及其应用［M］.北京:机械工业出版社，2005.

【2】蔡自兴.机器人学［M］.北京:清华大学出版社，2009.

【3】郑笑红，唐道武.工业机器人技术及其应用［M］.北京:煤炭工业出版社，2004.

【4】金振林，王军，高峰.新型6-PSS并联机器人工作空间分析［J］.中国机械工程，2002，13(13):1088-1090.

【5】张志涌.精通MATLAB 6.5版教程［M］.北京:北京航空航天大学出版社，2003.