基于ANSYS的2根拉索平行钢丝接触问题有限元分析

陈 璨,李 红

(1.四川外国语学院重庆南方翻译学院管理学院,重庆 401120;2.内蒙古科技大学建筑与土木工程学院,内蒙古 包头 014010)

基于ANSYS的2根拉索平行钢丝接触问题有限元分析

陈 璨1,李 红2

(1.四川外国语学院重庆南方翻译学院管理学院,重庆 401120;2.内蒙古科技大学建筑与土木工程学院,内蒙古 包头 014010)

由于2根钢丝接触问题可以作为整个拉索断面平行钢丝间接触问题的简化,故在用ANSYS有限元方法分析整个拉索断面平行钢丝排列模型的接触问题之前,运用经典理论解和ANSYS有限元方法对2根拉索平行钢丝间接触问题进行了较为详尽的分析,确定出了两根钢丝间的接触宽度、在接触面上产生的最大接触应力及分布等主要参数.同时,将2种分析方法得出的结果进行了对比,表明用ANSYS有限元方法求解接触问题是可行的,其求解的准确性和精度能够满足要求.

拉索平行钢丝;接触问题;ANSYS;有限元分析

0 引 言

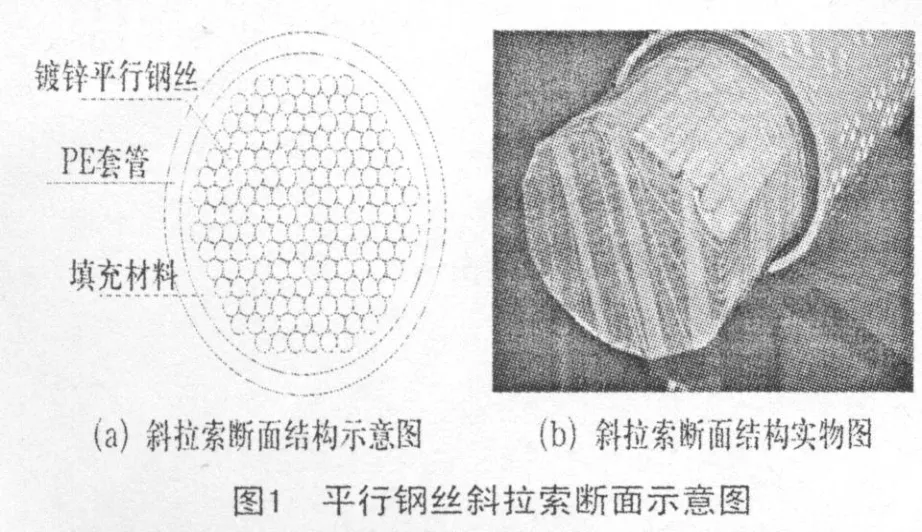
近年来,平行钢丝斜拉索因其独特的优点而广泛应用在斜拉桥的承重上.平行钢丝斜拉索内钢丝断面排列情况是复杂多样的(见图1),这对分析拉索因钢丝扭绞产生的钢丝间正压力的传递与分布带来了相当大的难度[1],目前尚不能进行精确的理论计算或参数化编程计算.由于2根钢丝接触问题是拉索平行钢丝间接触问题的最简化形式,只有将2根钢丝接触问题分析准确之后,才能在此基础上对多根钢丝间接触问题进行分析,或者对一根钢丝外包n圈钢丝简化模型接触问题进行分析,进而对整个拉索断面平行钢丝排列模型的接触问题进行分析.两根钢丝接触问题分析结果作为最基本的结果,也可用来检验对复杂问题的解决是否有效.故本研究运用经典理论解和ANSYS有限元方法对2根拉索平行钢丝间接触问题进行较为详尽地分析.

1 2根钢丝接触问题的描述及求解

1.1 问题描述

2根拉索平行钢丝接触问题描述如下:2根单位长度(这里取1 mm)、半径为3.5 mm的斜拉索镀锌平行钢丝(见图2),当在平行钢丝的轴线上施加均布荷载P=F/l=4 000 N/mm时,2根钢丝均会在压力的作用下产生相应的应力应变,特别是在2根钢丝的接触表面将会发生局部接触变形.那么,其接触的面积以及在接触面上产生的最大接触应力的大小可以根据接触问题经典理论解和有限元软件来求解.其中,平行钢丝的弹性模量 E1=E2=E=1.95×105MPa,v1=v2=0.3.

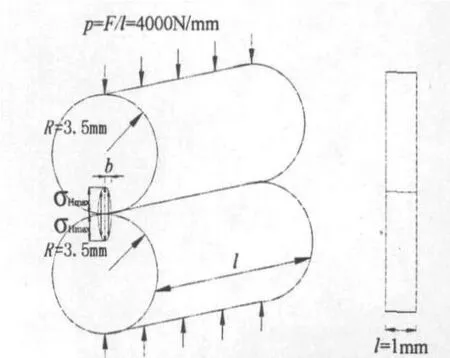
图2 单位长度的2根钢丝的接触

1.2 经典理论解

经典理论认为:对于2个长为 l,半径分别为R1、R2的圆柱体的接触(见图3),当没有任何压力作用于它们上时,2圆柱体只在其切平面上的一条线上有所接触.当沿圆柱体轴线上的均布荷载 P=F/l作用于圆柱体上时,2圆柱体间将形成面积为2 b×L的长方形接触面.其赫兹接触半宽b、最大接触应力 σHmax(接触面上的最大单位压力q0称为最大接触应力 σHmax)、接触相对位移 δ可按下列公式[3]计算:

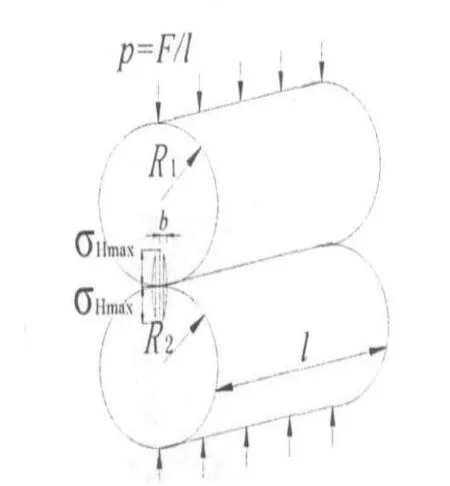
图3 2圆柱体接触

接触半宽b为,

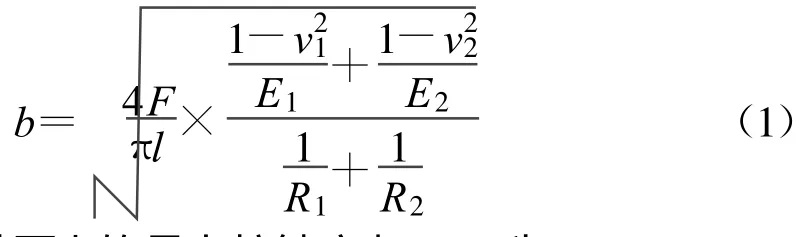
接触面上的最大接触应力 σHmax为,

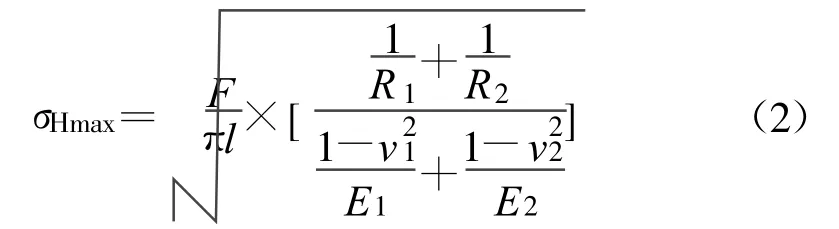
接触相对位移δ为,

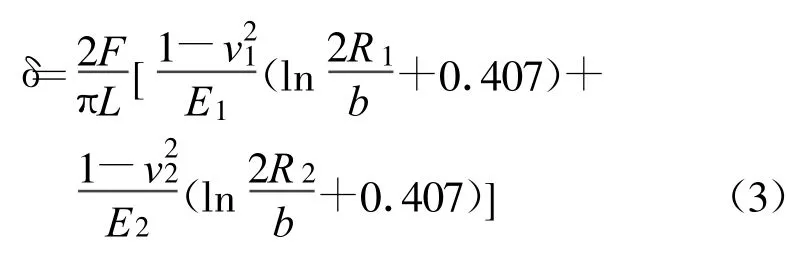
其中,E1、E2为2圆柱体材料各自的弹性模量;v1、v2分别为2圆柱体材料各自的泊松比.

当2圆体的材料相同,且泊松比均为0.3,即E1=E2=E,v1=v2=0.3时,接触半宽b为,

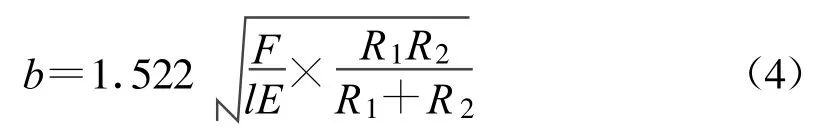
接触面上的最大接触应力 σHmax为,

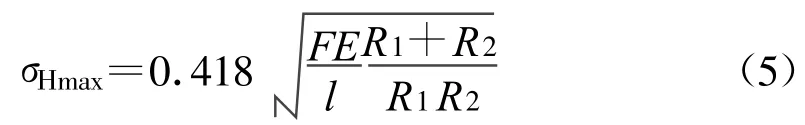
接触面上产生的接触应力的分布曲线近似为平滑的抛物线(见图3).

由于平行钢丝的几何特性,可近似求解2根钢丝的接触问题[3].根据式(4)、(5)得,在荷载 P=F/l=4 000 N/mm的作用下,2根钢丝间的接触半宽b=0.288367536 mm;最大 接 触 应力 σHmax=8 824.793644MPa.

1.3 ANSYS有限元解

1.3.1 有限元模型的建立.

由于实体单元建模划分网格时网格较多,故可将该问题简化为平面问题,并建立平面模型[4].所建模型的尺寸、材料参数和力学参数为:模型厚度取单位厚度(1 mm),圆的半径取3.5 mm,所加的荷载为4 000 N,材料的弹模取1.95×105MPa,泊松比取0.3.

在对模型进行网格划分时,为了确保计算精度,将模型划分成四边形网格.划分网格后模型的单元数为640,如图4所示(显示1mm厚度),图5为接触区域的网格划分情况.

网格划分完毕后,将2圆面接触区域建立接触,将此接触处理为面—面接触.同时,指定目标面和接触面,定义目标面、接触面并生成接触单元(见图6).其中,用ESURE命令建立接触对,用TARGE169单元在目标面上生成目标单元,用CONTA171单元在接触面上生成接触单元.建立接触后,模型单元数增加到了672个.接着,在上面一个圆面顶部的节点施加向下的竖向荷载F=4 000 N,同时,在下面一个圆面底部处施加X、Y方向的约束,如图7所示.

1.3.2 结果与分析.

合理地选择单元的接触刚度对于求解的收敛十分重要,即在ANSYS有限元分析程序中,需合理地选择罚刚度比例系数(FKN).FKN取值通常将在0.01～10之间,可尝试去寻找一个适当的FKN值,起始估计值FKN=0.1.FKN 分别取0.1、1、10、100.圆柱体材料的弹模为1.95×105MPa,对应的接触刚度分别为 1.95×104、1.95×105、1.95×106、1.95×107N/mm2.以最大接触应力为监控变量,分析结果见表1.

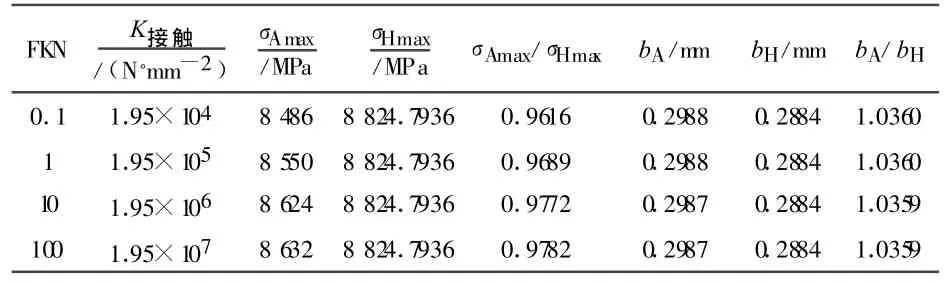
表1 不同接触刚度,2根钢丝模型ANSYS方法分析结果与理论值对比

表1中,FKN为罚刚度比例系数;K接触为接触刚度;σAmax为用ANSYS有限元方法得出的最大接触应力;σHmax为用赫兹经典理论得出的最大接触应力;bA为用ANSYS有限元方法得出的接触半宽;bH为用赫兹经典理论得出的接触半宽.用ANSYS有限元方法求解时,接触半宽bA可以通过公式(6)[5]得出,

式中,X′为处于接触状态的点中X坐标最大的点的X坐标值,U′X为该节点的X方向位移.

由表1可以看出,当FKN的值超过10时,结果不再发生显著的改变,即10为寻到的合适的FKN值.同时,将最大接触应力、接触半宽的ANSYS解与经典理论解对比可知:由ANSYS方法得出的结果和经典理论得出的结果非常接近,这表明用ANSYS方法求解接触问题是可行的,其求解的准确性和精度能够满足要求.

图8为2圆面接触区域附近的节点编号.由于模型的对称性,取Y轴左侧,接触区域下表面附近的节点作为研究对象,其节点编号参见表2.在提取接触区附近节点的求解结果时,需判断接触区域附近节点的接触状态.可以通过提取接触区域附近节点的节点反力FY来判断节点的接触状态,如果节点反力FY＞0时,则此节点处于接触状态,当FY=0时,此节点为非接触状态[6].节点的接触反力之和∑FY应为4 000 N.

图8 2圆面接触区域附近的节点编号

表2 接触刚度为1.95×106N·mm-2时,两根钢丝模型接触区附近节点ANSYS分析结果

图9为ANSYS分析得出的位移云图.

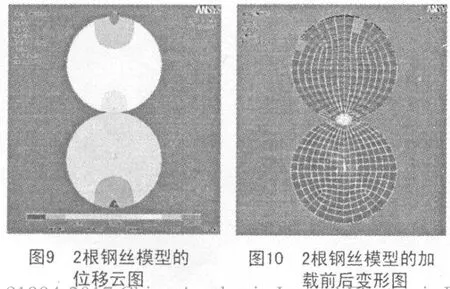
由图9可以看出,加力位置附近位移最大,2圆面底部加横向约束、纵向约束的位置附近位移为零,位移值至顶向下逐渐变小,接触区域附近相对位移值范围为0.0808～0.1010 mm.

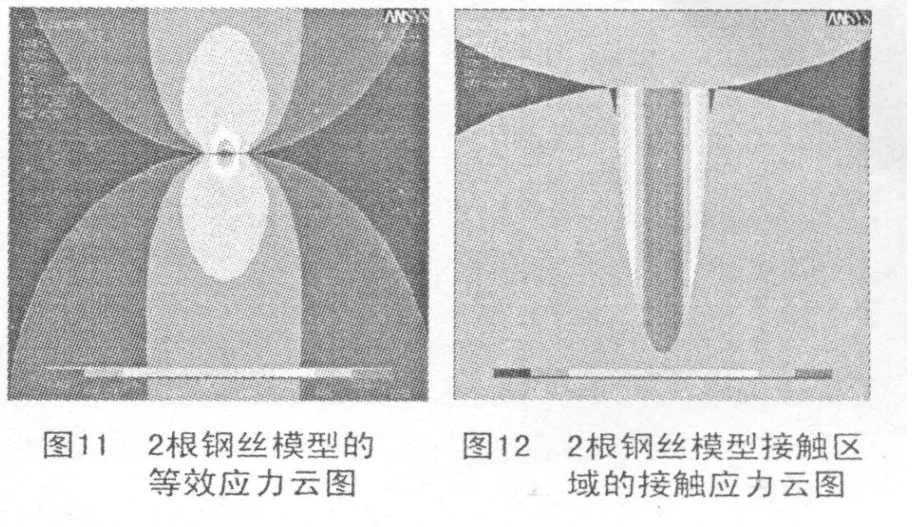
图10是加载前后的变形图,加力位置附近变形最大,变形至顶向下逐渐变小.图11为等效应力云图,最大等效应力值为8 262 MPa,最大等效应力位置位于接触区域附近.图12为接触区域的接触应力云图,其接触应力分布曲线近似为平滑的抛物线,这与经典理论解得出的接触应力分布曲线相一致.

当加大小不同荷载时,2根钢丝模型的最大接触应力σAmax、接触半宽bA、接触点节点反力之和以及接触区域附近节点的接触状况进行比较.结果如表3所示.

表3 加不同大小荷载时,2根钢丝模型的接触应力、接触半宽、接触区域附近节点的节点反力、接触状态

表3表明,随着所加荷载的增大,由ANSYS有限元方法分析得出的最大接触应力和接触半宽、接触区域附近节点的节点反力之和、节点进入接触状态的数目都有所增大.其中所加荷载增加到4倍,最大接触应力、接触半径只近似增加到2倍,即随着荷载的增加最大接触应力、接触半宽不是线性增加的.

这与接触问题经典理论解得出的结论:最大接触应力、接触半宽与所加载荷的1/2次方成正比(见公式(1)、(2))是相吻合的,这也表明用ANSYS有限元方法求解接触问题是可靠的.

2 结 论

本研究先后用经典理论解和ANSYS有限元方法对2根拉索平行钢丝接触问题进行了分析,并得出以下3点结论.

1)用ANSYS有限元方法分析2根拉索平行钢丝接触问题时,在合理选择接触刚度的基础上,得出2根钢丝间的接触宽度以及在接触面上产生的最大接触应力值和经典理论得出的结果是非常接近的.用ANSYS有限元方法分析得出的2根钢丝模型的位移云图、加载后变形图、等效应力云图及接触区域的接触应力分布曲线较为直观、清晰.分析发现,随着所加荷载的增大,由ANSYS有限元方法分析得出的最大接触应力和接触半宽、接触区域附近节点的节点反力之和、节点进入接触状态的数目都有所增大.

2)将2种分析方法的结果进行对比,验证了用ANSYS有限元方法求解接触问题是可行的,其求解接触问题的准确性和精度能够满足要求.

3)2根钢丝接触问题作为拉索平行钢丝间接触问题的最简化形式,对其分析结果的较好把握为接下来解决更加复杂的拉索平行钢丝间接触问题奠定了实践基础.同时,其分析结果也可用来检验对复杂问题的解决是否有效.

[1] 谢宜.考虑分层滑移的斜拉索弯曲应力的进一步分析[D].重庆:重庆交通大学,2009.

[2] 陆万明,罗学富.弹性力学理论基础[M].北京:清华大学出版社,1997.

[3] 李红.斜拉索内钢丝间联合工作模式对局部弯曲应力的影响[D].重庆:重庆交通大学,2010.

[4] 王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.

[5] 李峰,赵杰.应用ANSYS求解赫兹接触问题[J].机电产品开发与创新,2006,19(6):76-78.

[6] 王水林,邓建辉,葛修润.改进的拉氏乘子法在接触摩擦问题中的应用[J].岩土工程学报,1998,20(5):64-67.

Finite Element Analysis on Contact Problem between T wo Parallel Stay-cables Steel Wires Based on ANSYS

CHEN Canl,LI Hong2
(1.School of Management,Chongqing Nanfang Translators College of SISU,Chongqing 401120,China;2.School of Civil Engineering&Architecture,Inner Mongolia University of Science and Technology,Baotou 014010,China)

Contact problem of two steel wires is the simplest one of contact problems,so contact problem of two parallel steel wires of stay-cables is analyzed in detail using both the classic theoretical solution and the ANSYS finite element software before contact problem analysis of the parallel wires of the whole cable section by the ANSYS finite element software.Some major parameters,such as contact width,maximum contact stress and distribution of the maximum contact stress between two steel wires are determined.By comparing the results of both methods,we can find that ANSYS is feasible to solve the contact problem and the accuracy and precision of this solution can meet our requirements.

parallel stay-cables steel wire;contact problem;ANSYS;finite element analysis

U443.38

A

1004-5422(2013)01-0071-04

2012-12-19.

陈 璨(1987—),女,硕士,从事结构工程力学问题研究.