棉蚜种群模型的参数估计

朱成莲,高晓婷

(淮阴师范学院数学科学学院,江苏淮安 223300)

0 引言

棉蚜在全世界棉区都有分布,甚至可达北纬60°、南纬40°,可以说是一个生态幅度很广的种群,因而能够适应在多种多样的环境条件下生活[1].寄主植物有石榴、木槿、花椒、瓜类等.棉蚜每年发生十几到三十几代,由北往南代数逐渐增加.棉蚜以刺吸式口器在棉叶背面和嫩头部分吸食汁液,使棉叶畸形生长,棉叶向其背面卷缩,影响正常光合作用的受光面积,减少干物质的积累.棉蚜排泄蜜汁,茎叶及嫩段呈现一层污黑的覆盖物,影响光合和呼吸作用的功效.影响叶片的光合作用,在幼苗期和蕾铃期,推迟棉苗发育,造成晚熟减产,害虫严重时能使棉苗不能继续发育甚至死亡,蕾铃期为害的棉花,会使蕾铃脱落,甚至造成棉花落叶而减产,棉花吐絮期间有时还有棉蚜为害,这时棉蚜的排泄物污染棉絮,降低棉花品质,致使纺织程序上发生罗拉现象[2,3],因此,控制棉蚜的危害不仅是植棉的需要,也是棉纺企业的要求[4].棉蚜排泄诱发腐生霉菌,更重要的是还能传播多种植物病毒病.20世纪60年代农药的迅速发展,高效广谱农药相继出现,几乎所有主要害虫均可以用农药防治[5],农药遂成为防治棉虫的主要手段,过多地依赖农药致使害虫产生了抗药性,同时化学农药造成的环境严重污染,另一方面由于化学农药的不恰当使用而大量杀伤天敌,使其失去对棉蚜的抑制作用,防治害虫的目的一般不是灭绝害虫,而是控制其发生的数量,使其不足够造成经济上的危害.因此害虫防治实质上是控制害虫数量变动的工作.

为了防治棉蚜,许多学者就棉蚜成灾规律和种群动态模型进行了大量的研究[6-16],赵惠燕、汪世泽、赵鼎新、周丽丽等1983、1988、1993分别建立了棉蚜种群动态模型[17,18],张文军、汪世泽[12]等1988研究了棉蚜种群数量变动规律,建立了棉蚜种群动态预报模型等等.本文旨在研究棉蚜种群数量模型参数估计,更好掌握棉蚜的数量增长规律.为棉蚜防治工作提供理论依据.

1 棉蚜数量动态的模型

害虫发生规律的主要问题是种群的数量变化动态.因为一种昆虫是否对农作物有害,或者是否造成经济损失,要看虫口密度的大小,特别是对于间接害虫,当虫口数量很少时,即使对农林作物造成某种损伤,但它并不一定给人们带来经济损失.相反,如果虫口数量很多,足够造成经济损失,那么,这种昆虫就成了所谓害虫,必须某种防治措施了.因此我们在研究害虫发生规律以指导防治时,应当注意害虫的数量变化动态,在棉蚜数量的变化动态过程中,棉蚜数量变化具有趋势性,同时其也具有周期性.棉蚜种群在数量变化动态过程中,分为好几个小的周期.在每个周期内,其数量的变化模型可以用经典意义下的Logistic方程与反Logistic方程来描述.

从棉蚜的发育阶段来看,在棉蚜数量增长的第一阶段也就是苗蚜的阶段,由于环境、气温等因素干扰相对小一些,增长曲线表现出很好的s型曲线,该曲线可以由Logistic方程来给定[19],即

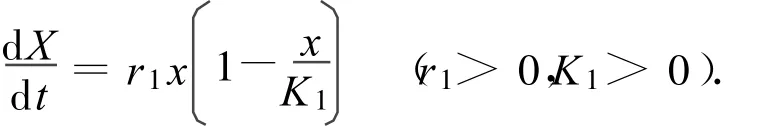
Logistic方程最初由Verhulst,Pearl与Read最早彼此独立推导出来,故亦称Verhulst-Pearl方程[20-22].其微分形式为

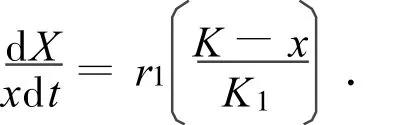
该方程初值问题X(0)=X0的解为

其中

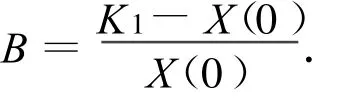
在苗蚜及伏蚜数量的绝迹阶段,其数量不断减少,这时模型可以由反Logistic方程来描述,即

反Logistic方程的微分形式为

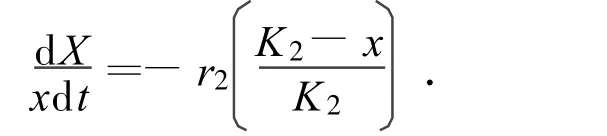
该方程初值问题X(0)=X0的解为

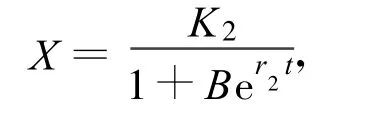
其中

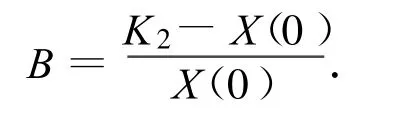
在秋蚜数量增长阶段,此时气温、季节对其有着重要影响,造成波动,然而其增长模型仍然可由Logistic曲线来给定(r3＞0,K3＞0)[19],

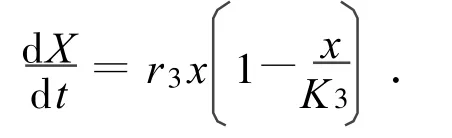
2 棉蚜数量动态的模型参数估计

为了给棉蚜的综合防治提供理论依据,棉蚜种群增长规律符合Logistic增长模型及反Logistic增长模型,利用实测数据对模型的参数进行估计,能较好地预测棉蚜的种群动态,及时做好防治工作.下面分两种情况,一种实测数据较少,实测数据较多.对Logistic增长模型

的参数进行估计.

若实测数据较少,在原始资料中选3点(t1,X(t1))、(ti,X(ti))、(tn,X(tn)),且满足将它们分别代入(1)式,得到

由式(2)减去式(4)化简得

由式(5)减去式(7)化简得

由式(8)除以式(9)得

由式(9)除以式(10)得

由式(11)除以式(12)得

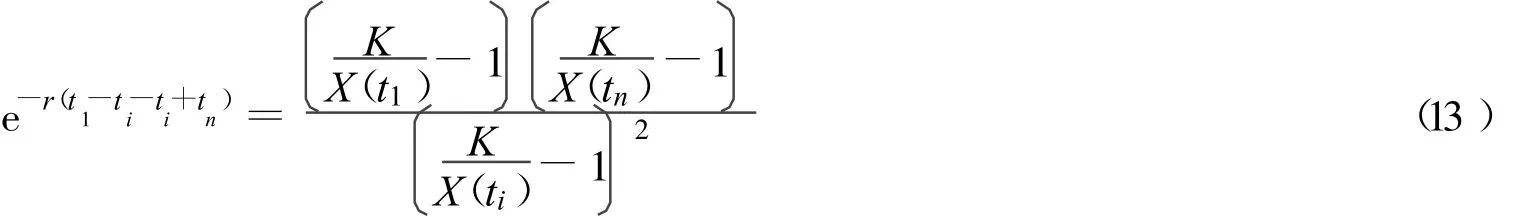
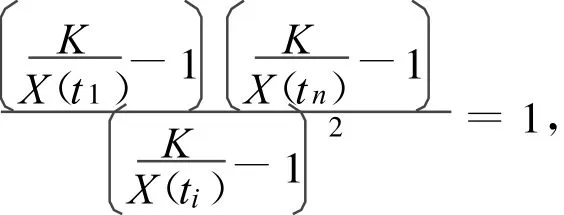
解得

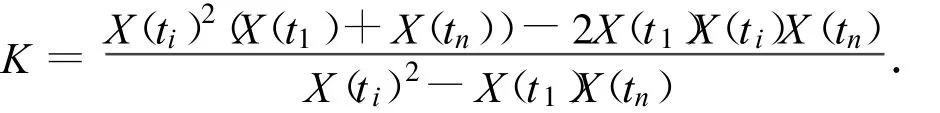
下面求解B和r,由

得

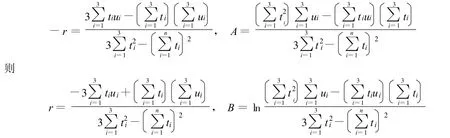
所以K,B,r的估计为

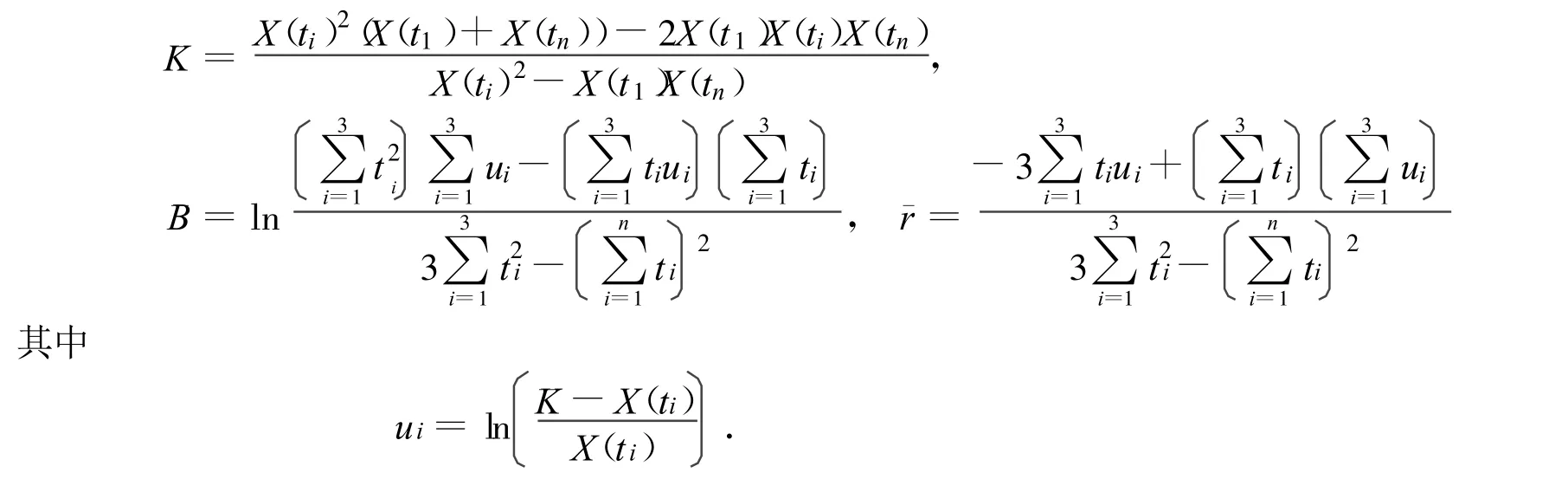
若实测数据较多,将整个实测序列数据分成时间间隔均相等的三段,且相邻观测时间间距相等Δt,由三段观察值序列之和经过推导运算来估计模型参数,选择近期实测时间序列数据X(x0),…,X(xn-1);X(x2n),…,X(x2n-1);X(x3n),…,X(x3n-1)顺序截取长度为n的三段,将变形为

将三段数据代人(15)分别求和得

另外，对于改编成以儿童为阅读对象的文学作品，虽然《中图法》已明确规定应归入儿童文学有关类目，但在实践中，由于作品改写幅度的大小难以鉴定，加上分编人员往往不愿意将此类作品与原作品分散，于是许多名著改写本还是归入“成人文学”类［8］。

由式(16)减去式(17)得

由式(17)减去式(18)得

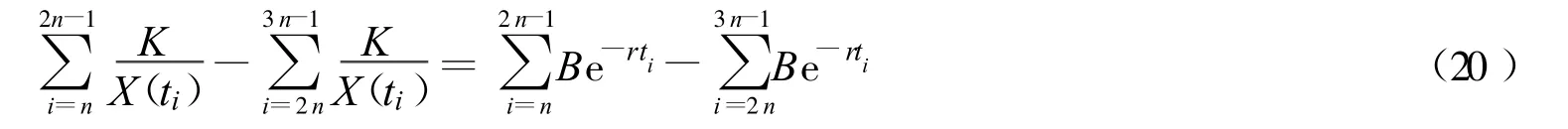
由式(19)除以式(20)得

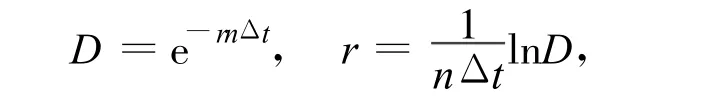
其中

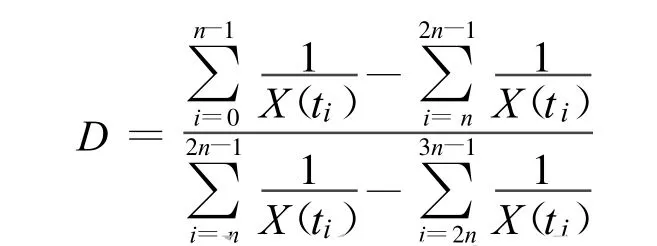
由式(16)减去式(17)得

由式(21)除以式(22),再将r代入,得

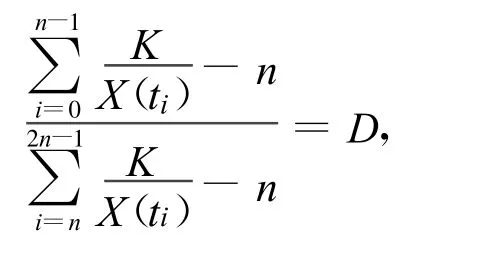
即

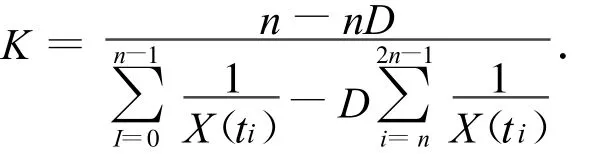
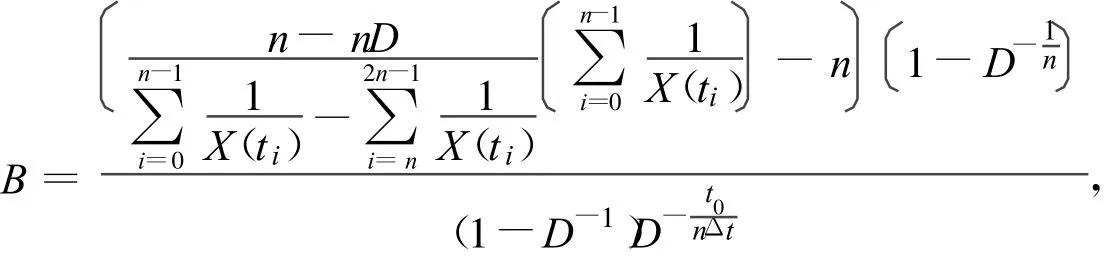
所以K,B,r的估计为

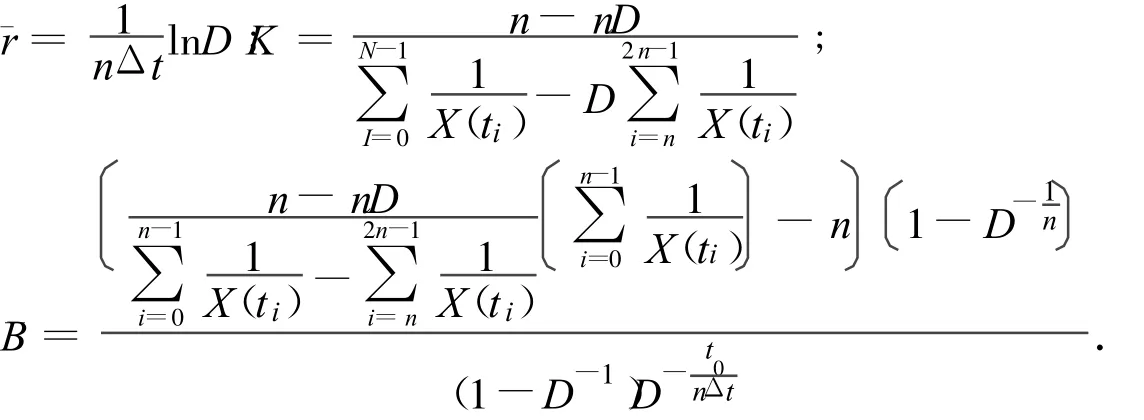
其中

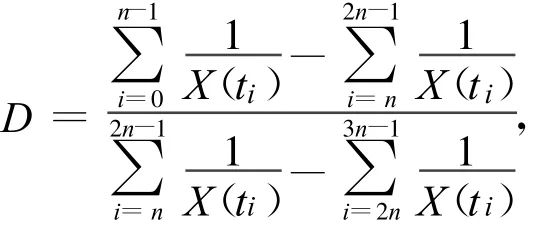
对于反Logistic增长模型

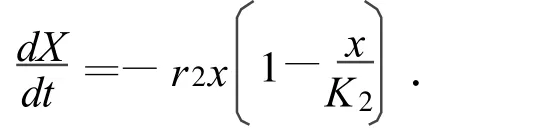
选取三点(t1,X(t1))、(ti,X(ti))、(tn,X(tn)),且满足时,K2,B2,r2估计分别为

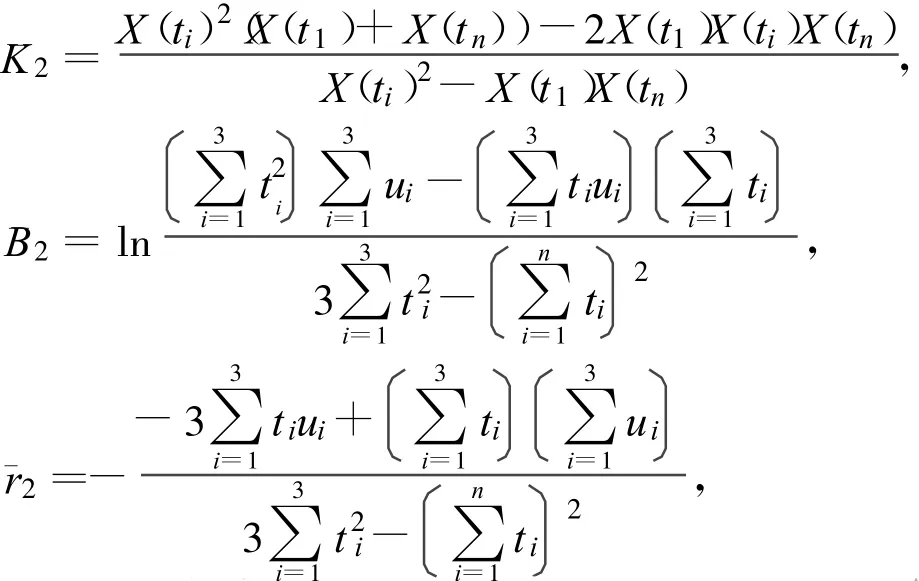
其中

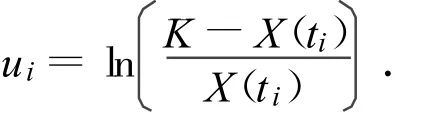
对于反Logistic增长模型

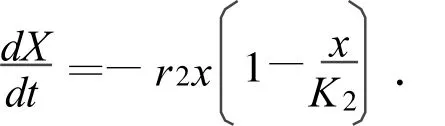
选取多点将整个实测序列数据分成时间间隔均相等的三段,且相邻观测时间间距相等Δt,实测时间序列数据X(x0),…,X(xn-1);X(x2n),…,X(x2n-1);X(x3n),…,X(x3n-1)顺序截取长度为n的三段,K2,B2,r2估计分别为

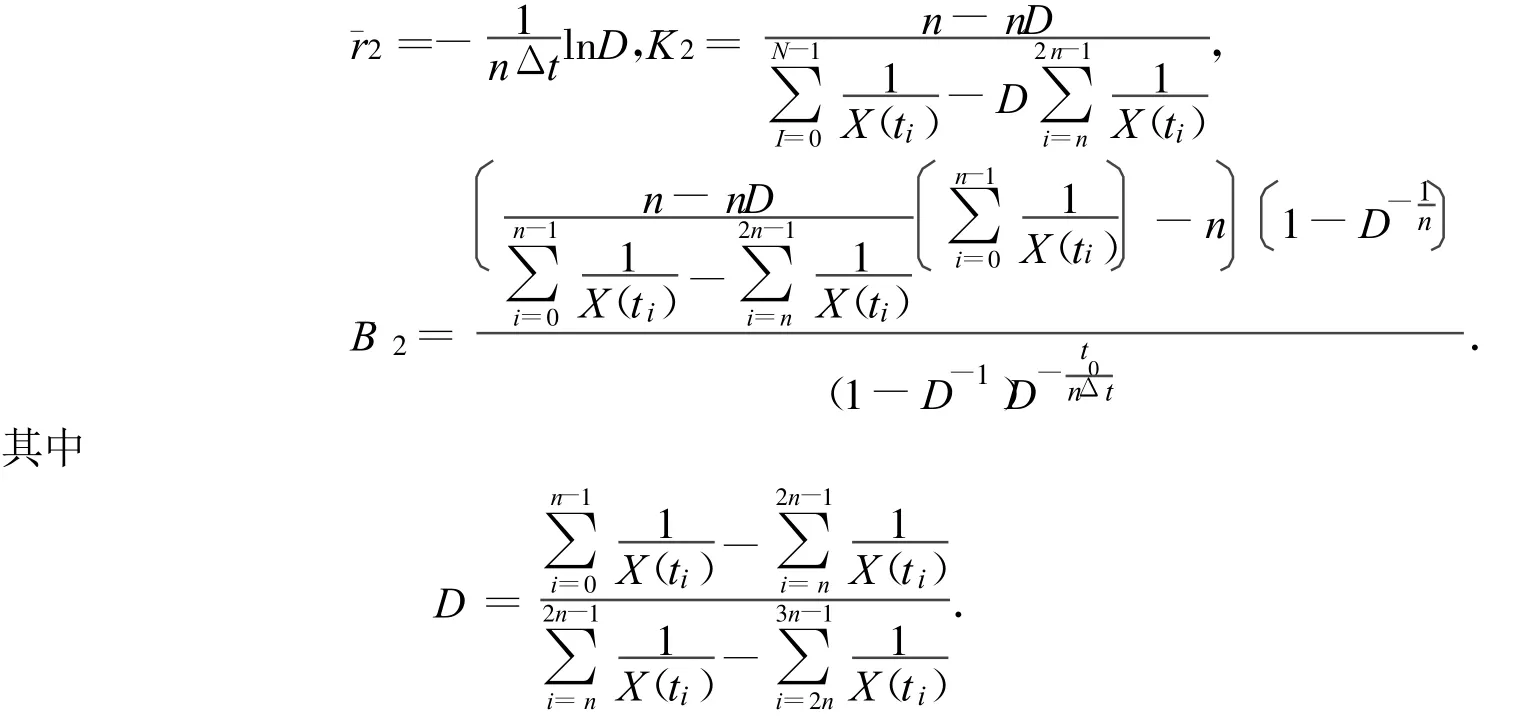
这样可以根据实测数据,预测棉蚜增长模型,及时出棉蚜随时间变化的数量,采取恰当的措施,及时做好棉蚜的防治工作.

[1] 张孝羲,赵静雅,张广学,等.棉蚜种群寄主转换的适应和变异规律研究[J].生态学报,2001,21(1):106-111.

[2] 中国农作物病虫害编辑委员会编.中国农作物病虫害[M].上册.北京农业出版社,1979.

[3] Smaal A C,Prints T C,Dankers N,et al.Minimum requirements for modeling bivalve carrying capacity[J].Aquatic Ecology,1997,31(4):423-428.

[4] 丁世飞,陈建.应用统计分辨原理预报害虫种群动态[J].应用概率统计,1998,3(14):333-335.

[5] 曹赤阳.中国棉花害虫综合防治的新进展[J].昆虫知识,1992,29(3):170-171

[6] 李林.一个描述昆虫的数学模型的定性分析[J].生物数学学报,2003,8(2):182-186.

[7] 赵惠燕,汪世泽.棉花苗蚜尖角突变模型及其分析[J].生态学报,1997,34(3):144-146.

[8] 邹运鼎,毕守东,陈高潮,等.棉花棉蚜种群动态及瓢虫对棉蚜种群数量的影响[J].应用生态学报,1998,9(5):499-502.

[9] 靳桂芝.运用模糊数学预棉花苗期棉蚜发生量[J].昆虫知识,1997,4(3):144-146.

[10] 黄春明,古风启,葛兰芬.棉讶发生规律及天敌控制效应[J].石河子科技,1995,20(1):49-511.

[11] 戈峰,谢宝瑜.不同类型棉田棉蚜种群动态研究[J].昆虫知识,1995,34(3):144-146.

[12] 张文军,汪世泽.棉蚜种群数量模拟的初步研究[J].生态学杂志,1990,9(5):26-28.

[13] 吴孔明,赵炳宜.棉蚜种群动态预报模型[J].应用生态学报,1994,5(3):287-291.

[14] 赵中华,沈佐锐.昆虫种群动态非线性建模理论与应用[J].生物数学学报,2001,16(4):439-447.

[15] 邢黎峰,孙明高,王元军,等.生物生长的Richards模型[J].生物数学学报,1998,13(3):348-353.

[16] 赵鼎新,周丽丽.棉花苗期棉蚜种群动态初探[J].昆虫知识,1988,25(2):79-80.

[17] 汪世则,赵慧燕,董应才.棉蚜体色分化与季节生物型问题[J].西北农学院学报,1983,11(2):9-23.

[18] 赵惠燕,张改生,汪世泽,等.棉蚜体色变化的生态遗传学研究[J].昆虫学报,1993,36(3):282-289.

[19] 郑立飞,赵惠燕,刘光祖,等.棉蚜种群数量动态模型[J].生物数学学报,2008,23(2):306-310.

[20] HutchinsonG E.An Introduction to Population Ecology[M].New Haven:Yale University Press,2002.