无穷时滞非线性脉冲积分微分系统的概周期解

卢钰松，林远华

(河池学院 数学系，广西 宜州 546300)

1 引言和主要结果

泛函微分方程的周期解的存在问题一直是大家所关心的问题［1－3］，近年来，对于中立型泛函微分系统的研究也引起了学者们的广泛关注。在许多实际问题中，要对其进行准确的描述，就必须同时考虑时滞和脉冲对系统的影响，这在研究时滞脉冲微分方程解的性态上具有更重要的现实意义，本文利用不动点方法并结合不等式分析技巧将文献［4－6］中的微分方程推广到时滞脉冲概周期系统。

考虑概周期脉冲系统

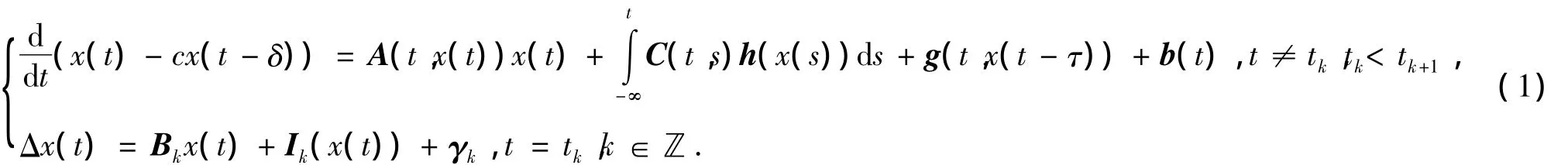
的概周期解的存在性。

这里 x∈ ℝn，A(t，x(t))，C(t，s)为 n × n 连续函数矩阵，h，g，b，为连续函数向量。Bk是矩阵序列，Ik为向量函数序列，γk为n维向量

对于系统(1)给出如下假设:

H1:A(t，x)关于t概周期的，即对∀ε＞0，对∀t∈ℝ，使得

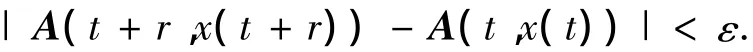
H2:矩阵序列{Bk}是概周期的，即对∀ε＞0，∃q∈ℤ，使得|Bk+q－Bk|＜ε.且行列式|E+Bk|≠0，这里E是单位矩阵。

H4:函数b(t)是概周期的，即对∀ε＞0，对∀t∈ℝ，使得|b(t+r)－b(t)|＜ε，{γk}也是概周期序列，即对∀ε ＞0，∃q∈ℤ ，使得|γk+q－γk|＜ ε.且存在正常数C0使得max{sup|b(t)|，max| γk| }≤C0.

H5: C( t，s) 是概周期的，即对∀ε ＞ 0，对∀t，s ∈ ℝ ，使得| C( t + r，s + r)－C( t，s) | ＜ ε. 且∀t，有

H6:函数h(x)在ℝ 上满足Lipschitz条件，即∃L1＞0，使得对∀x，y∈ℝn，都有|h(x)－h(y)|≤L1|x－y|.

H7:g(t，x)关于t是概周期的，即对 ∀ε ＞ 0，对 ∀t∈ ℝ ，使得 |g(t+r，x)－g(t，x)|＜ ε.且满足Lipschitz条件，即 ∃L2＞ 0 使得对 ∀x，y∈ ℝn，都有 |g(t，x)－ g(t，y)|≤ L2|x－y|，并有 g(t，0)=0.

H8:函数序列Ik(x)关于x∈ℝn是一致概周期的，即对∀ε＞0，∃q∈ℤ 使得|Ik+q(x)－Ik|＜ε.且Ik(x)满足Lipschitz条件，即∃L3＞ 0，使得对∀k∈ℤ ，x，y∈ℝn，都有|Ik(x)－Ik(y)|≤L3|x－y|，并有Ik(0)=0.

定理1 如果下列条件满足

(Ⅰ)条件H1～H8成立;

(Ⅱ)对任意连续概周期函数u(t)，线性系统x(t)=A(t，u(t))x(t)满足投影为P和常数为K，λ的指数型二分性，且二分常数K，λ不依赖于u(t);

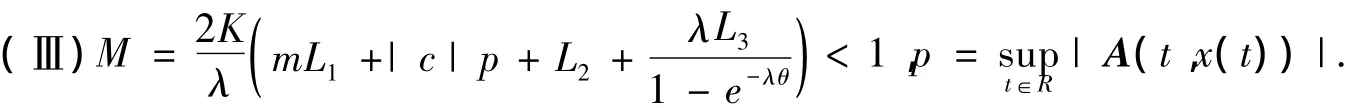
那么方程(1)存在唯一的概周期解x(t).

注:我们将文献［4－6］的周期系统推广到了概周期系统，得到了保证中立型系统概周期解存在性和唯一性的定理，由于周期函数是概周期函数的特例，因而我们推广了文献［4－6］的相关结果，即使是在脉冲效应消失的情况下，也推广了相关的结果。

2 准备知识

定义1［7］称序列的集合是一致概周期的，如果对∀ε＞0，对每个序列都存在共同的ε－概周期的相对紧集。

定义2［7］函数φ(t)∈PC(ℝ，ℝn)称为概周期函数，如果

(1)序列［tk］是一致概周期的，即对∀ε＞0，∃j∈ℤ，使得|tk+j－tk|＜ε.

(2)∀ε ＞ 0，∃δ＞ 0，使得t'，t″属于 φ(t)的同一连续区间，当 |t'－ t″|＜ δ时，满足|φ(t')－ φ(t″)|＜ ε.

(3)∀ε ＞0，存在一个相对紧集Q，对r∈Q，有|φ(t+r)－ φ(t)|＜ ε，这里|t－tk|＞ ε，k∈Z.集合Q中的元素称为φ(t)的ε—概周期。

考虑如下方程

和

这里A(t)是n×n概周期函数矩阵，Bk是概周期矩阵，即对任意给定的ε＞0，存在q∈ℤ，使得|Bk+q－Bk|＜ ε，同时行列式 |E+Bk|≠0，|γk+q－ γk|＜ ε，ε 是任意给定的正数，k，q∈ ℤ .

由文献［8］知，如果Uk(t，s)是系统

的柯西矩阵，那么系统(2)的柯西矩阵表示为

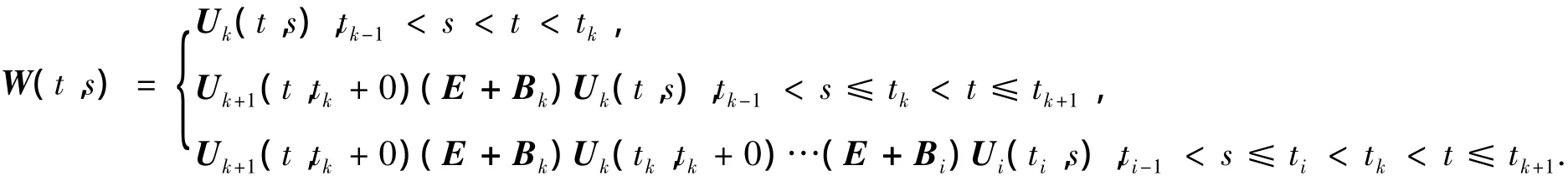
且系统(2)的解可以写成如下形式

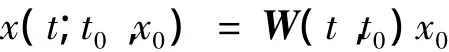
引理1［7］假设W(t，s)是脉冲概周期系统(2)的柯西矩阵，f(t)是n维向量概周期函数，γk是概周期序列，A(t)是矩阵概周期函数，Bk是概周期矩阵且行列式|E+Bk|≠0，则系统(3)存在唯一的概周期解，它可以表示为

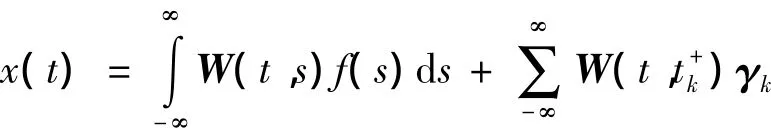
引理2［7］若存在正数K和λ，使得

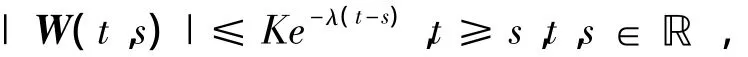
则对∀ε ＞0，t∈ℝ，s∈ℝ ，t≥s，|t－tk|＞ ε，|s－tk|＞ ε，k∈ℤ ，且存在一个与矩阵A(t)的ε－概周期相关的致密集T和一个正常数Γ，使得对r∈T，有|W(t+r，s+r)－ W(t，s)|≤ εΓe－(λ/2)(t－s)

3 定理的证明

定理1的证明:我们定义D={u(t):u∈PC，且u(t)为概周期函数}，并满足

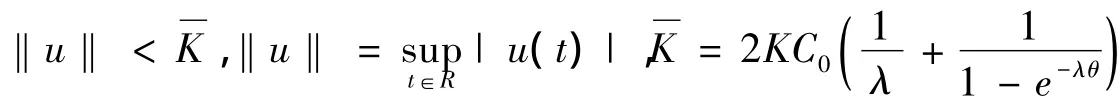
由条件(Ⅱ)和引理1可知，该系统存在唯一的概周期解

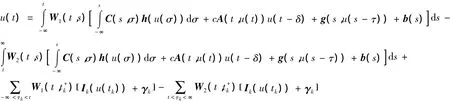
其中由条件(Ⅱ)，这里 W1(t，s)=X(t)PX－1(s)，W2(t，s)=X(t)(I－P)X－1(s)，也有 |W1(t，s)|≤Ke－λ(t－s)(t≥ s)，|W2(t，s)|≤ Ke－λ(s－t)(s≥ t). 在 D 中定义算子 S 如下

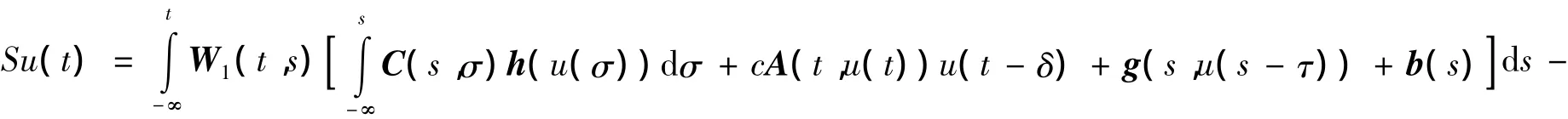
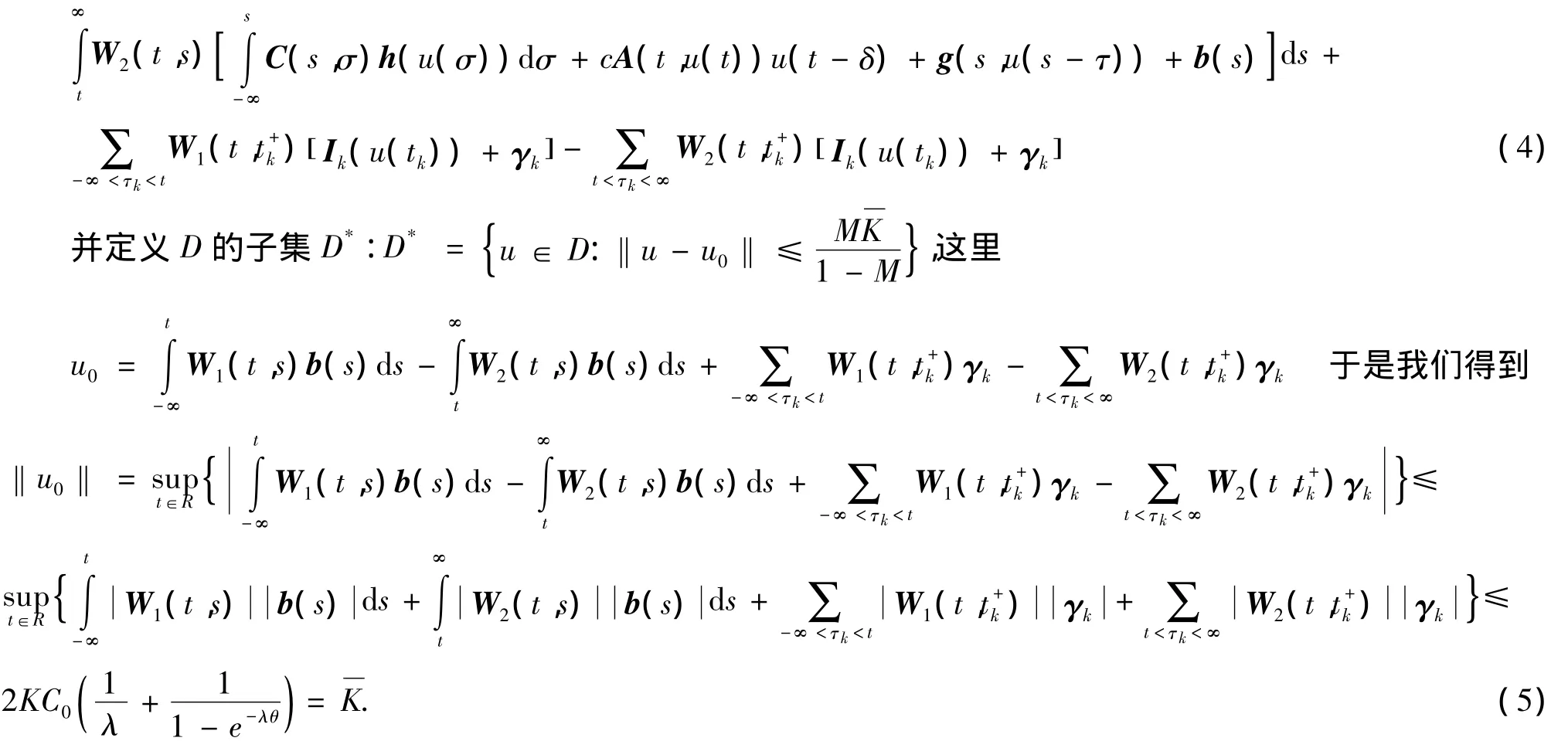
那么对任意的u∈D*，由(4)和(5)有

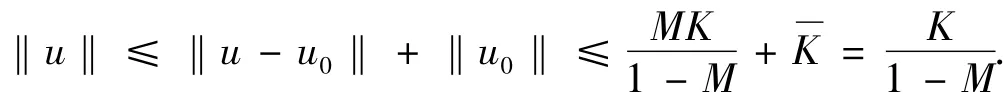
现在我们证明S是D到D的算子。

对任意的u∈D*，得到

并且对u∈D*，r∈ℤ，也得到

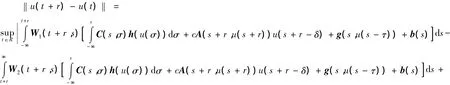
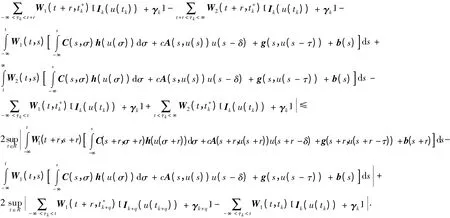
由此我们得到

既然ε充分小，那么εr也充分小，由(5)和(6)两式我们知道Su∈D*，即S是D*到D*的算子。又对任意的u∈D*，v∈D*我们也有

因为M ＜1，所以S是D*内的压缩算子，利用压缩映射原理知，S在D*中必存在唯一的不动点x(t)，所以方程(1)存在唯一的概周期解。证毕。

4 例子

考虑系统

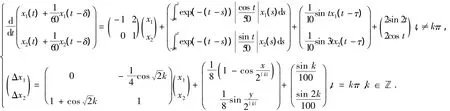
［1］王克.一类具偏差变元的微分方程的周期解［J］.数学学报，1994，37(3).

［2］曹进德，李琼.具时滞的高维周期系统周期解的存在性与唯一性［J］.数学学报，1997，40(2).

［3］周宗福.一类高维滞后型泛函微分方程的周期解［J］.数学杂志，2002，22(4).

［4］贺明科.一类中立型高维微分系统的周期解［J］.数学学报，1999，42(2).

［5］胡永珍，斯力更.具有无限时滞的中立型高维周期微分系统的周期解［J］.数学学报，2005，48(2)

［6］陈凤德.具无限时滞的非线性积分微分方程的周期解［J］.应用数学学报，2003，26(1).

［7］Samoilenko A M，Perestyuk N A.Differential equations with impulse effect［M］.Visca Skola:Kiev，1987.

［8］Bainov D D，Simeonov P S.Theory of impulsive differential equations:periodic solutions and applications［M］.Harlow:Longman，1993.

［9］Stamov G T.Impulsive cellular neural networks and almost periodicity［J］.Proc.Acad，2004，80(A).