单相短路时变压器角接绕组零序电流暂态特性及其影响

张军如，徐国俊，李 爽，鲁旭臣，韩洪刚

(1．华北电力大学，河北 保定 071003;2．辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006;3．沈阳工程学院，辽宁 沈阳 110136)

在220 kV及以上电力系统，变压器联接组别都采用YNd11连接，单相接地短路是电力系统常见故障之一。对于中性点直接接地的变压器，短路电流直接影响变压器主绝缘和纵绝缘［1－3］。国内曾发生过多起因单相短路而造成变压器绕组损坏事故，给电网带来重大损失。因此，有必要从暂态方面来研究零序电流对变压器绕组的影响。

短路发生时，零序电流除了对一次绕组产生影响外，同时还会影响到二次绕组。用对称分量法计算出的零序电流是在稳态时的值，不能反映出突发短路时零序电流对绕组的暂态冲击响应。对于三相一体式变压器，不能直接测出角接绕组中的零序电流。关于角接绕组中零序电流的计算方法，许多学者做了大量相关方面的研究［4－8］，但重点并不是研究其对绕组的影响，而是侧重变压器瞬时等效电感的计算，进而计算出空载合闸时励磁涌流。

1 计算模型推导

图1为联接组别为YNd11变压器绕组示意图。当发生单相接地短路时，各绕组将流过相应的短路电流，一次侧高压绕组可列出如下的微分方程:

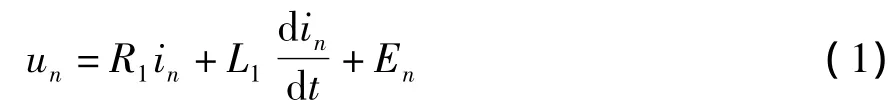
式中 un——一次绕组端电压;

In——流过一次绕组的电流;

En——各绕组的感应电动势 (n=A、B、C);

R1——一次绕组的电阻;L1——一次绕组漏电感。

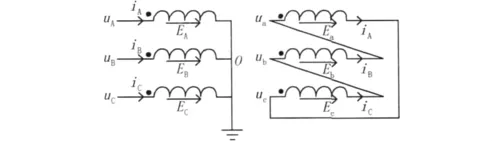
图1 YNd11变压器绕组连接示意图

根据T形等效电路原理，将变压器二次侧归算到一次侧，列写微分方程如下:

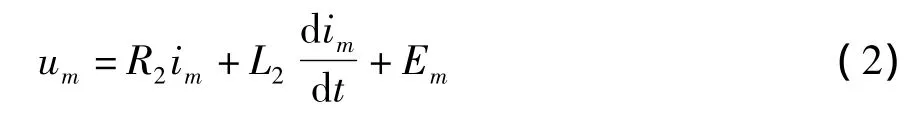
式中 um——二次绕组归算到高压侧的端电压;

Im——流过二次绕组归算到高压侧绕组的电流;

Em——二次各绕组归算到高压侧的感应电动势 (m=ac、ba、cb);

R2——二次绕组归算到高压侧的电阻;

L2——二次绕组归算到高压侧的漏电感。

由对称分量法可知，式 (1)、式 (2)有以下边界条件:

式中 u0——一次侧母线零序电压;

i0——变压器一次绕组零序电流;

ih——二次侧绕组归算到高压侧零序环流。结合上述4个边界条件，将式 (1)、式 (2)相加得:

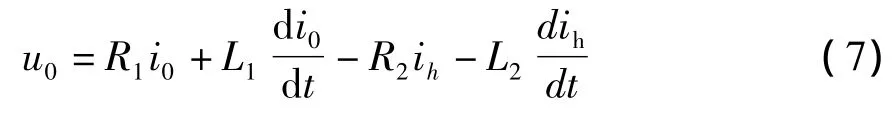
整理得:

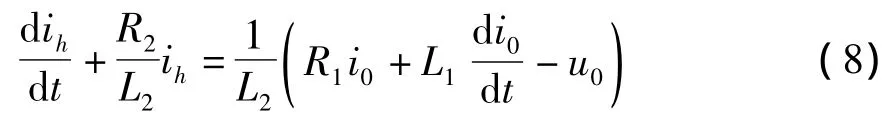
式 (8)属于一阶常系数非齐次微分方程，其解为

为便于程序编写，对式 (9)进行数值离散，得:

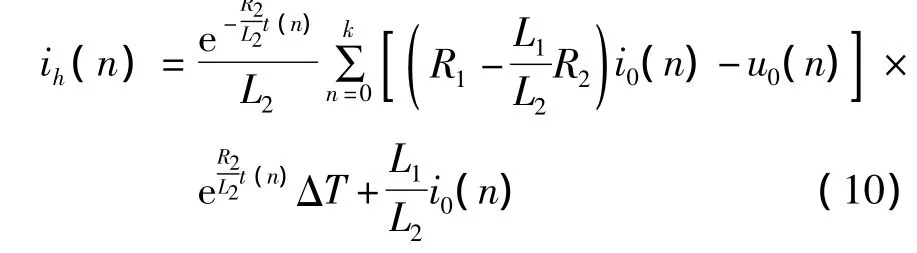
式中 n——计算的时间节点;

k——计算的终止时间;

ΔT——时间步长。

考虑到归算后，一、二次绕组的R1=R2、L1=L2，因此，式 (10)还可简化为

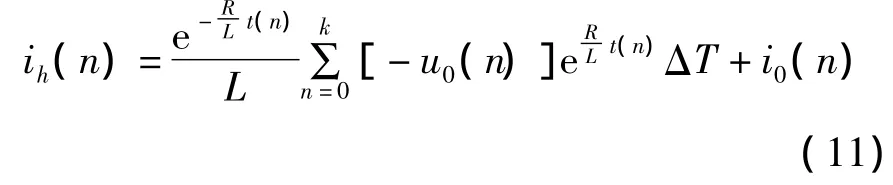
式 (11)就是所求的变压器角接绕组中归算到一次侧的暂态零序电流，角接绕组中实际的暂态零序电流还需在此基础上乘以变压器的变比。式(11)中的u0、i0还可从故障录波器上直接读取。

2 实例计算及分析

图2为某220 kV系统主接线图，E1、E2、E3分别为220 kV电网等值电源，等值电抗为34.54 Ω;1号、2号甲乙线为输电线路，其中1号线R1=1.268 4Ω、X1=7.263 9Ω、R0=3.339 4Ω、X0=12.544Ω、C1=0.162 3μF、C0=0.115 5 μF，输电线长26.47 km;2号甲线 R1=0.796 9 Ω、X1=5.106 9Ω、R0=2.575 1Ω、X0=9.527 4 Ω、C1=0.794μF、C0=0.111 3μF，输电线长11.47 km;2号乙线R1=0.823 187Ω、X1=3.872 Ω、R0=3.347 3Ω、X0=9.196Ω，输电线长12.42 km;T1、T2为2台同型号、同参数的变压器，变比为1.9，铭牌参数为Uk(%)=13.68、I0(%)=0.08、P0=88.4 kW、Pk=307.4 kW。

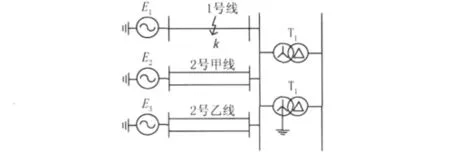
图2 某220 kV系统主接线图

假设A相发生单相对地短路。在1号线距变电站10 km处设置单相短路点，电弧电阻为0.01 Ω，在0.2 s时发生故障，故障持续时间0.2 s，故障时电源的初相位是90°。本文只考虑零序分量，故负载可忽略不计。如果变压器中性点不接地，其绕组中不会有零序电流，因此只有T2变压器绕组中才有零序电流。图3为发生单相接地短路时的电流波形。

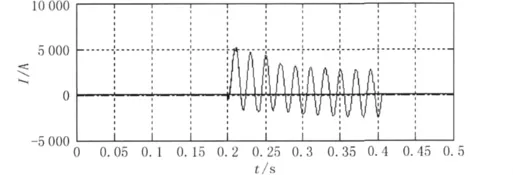
图3 单相接地短路电流波形

根据式 (11)计算得到变压器T2角接绕组中零序电流及频谱如图4所示。图4同时示出了本文方法和MATLAB/Simulink仿真结果的对比波形图。由波形图可以看出，本文的计算结果比仿真结果要大些，这是由于本文的计算方法没有考虑变压器励磁特性的影响，而在仿真模型中加入了变压器的励磁特性，因此造成差异。但两者波形的趋势吻合的很好。

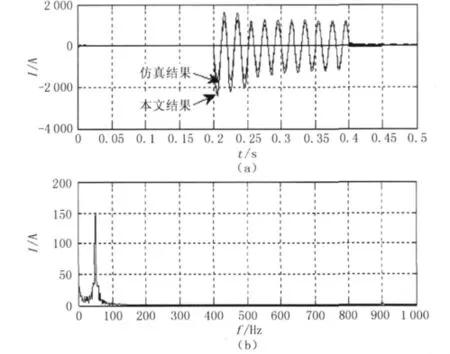
图4 单相接地时变压器角接绕组中的零序电流

由图4可知，零序电流中出现了零点漂移，包含有直流分量，这是由变压器的时间常数决定的。当电弧熄灭时引起了高频振荡，频率约在900 Hz，不过其幅值很低，不会对绕组绝缘带来伤害。但高频会使绕组的匝间容抗或层间容抗变小，对绝缘的薄弱处容易造成绝缘击穿［13－17］。

3 间歇性电弧接地对角接绕组零序电流的影响

假设系统发生3次间歇性电弧接地短路 (如图5所示)。图6为两种方法的计算结果，由图6可见，两者基本一致。

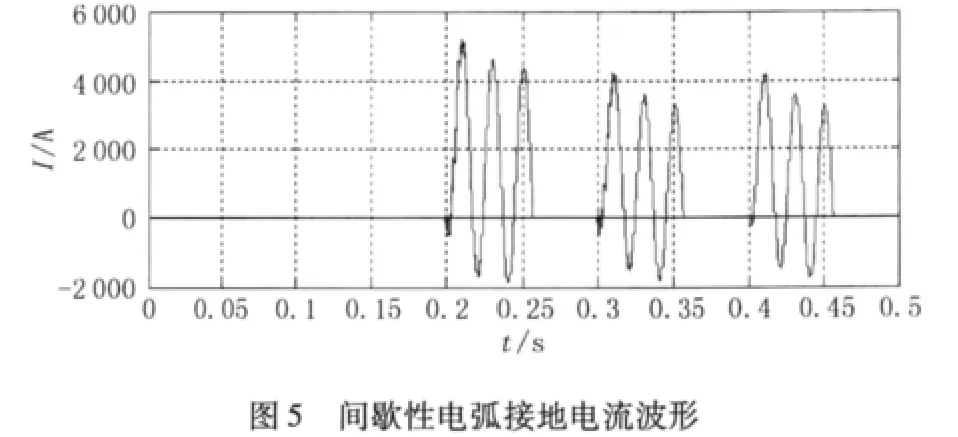
图6(b)说明在间歇性电弧接地情况下，系统包含了多种频率成分，有分频也有高频，说明间歇性电弧接地对电力系统的损害比单相接地故障大很多。这也是间歇性电弧接地容易引起系统谐振的主要原因。

在电弧熄灭瞬间引起了高频振荡，频率在900 Hz。从电流波形可知，第1次燃弧时峰值最高，以后发生的燃弧峰值有所下降，最终趋向稳定。

4 影响绕组中暂态零序电流的因素

根据单相对地短路的边界条件可知:正序、负序、零序电压的和为0，正序、负序、零序电流分量相等。由此可得零序电压和零序电流的表达式为

式中 Z1、Z2、Z0——分别为系统的正序、负序、零序等值阻抗;

Uf0——短路前的电源电压。

将式 (12)代入式 (11)，得:

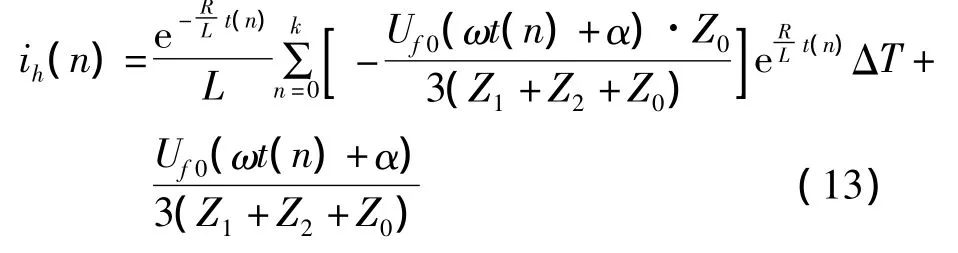
由式 (13)可知，暂态零序电流与电源的初始相角α、变压器绕组的电阻和漏感 (即时间常数(τ=L/R))及系统正序、负序、零序等值阻抗(即短路点的位置)有关。

4.1 电源初始相角对ih的影响

图7为变压器角接绕组中零序电流与电源初始相角的关系图。分别计算了初始相角为0°、60°、90°、120°、180°时的零序电流。从波形图可以看出，零序电流与电源初始相角的关系很大，α=0°和α=180°、α=60°和 α=120°时的电流波形相对于时间轴对称。

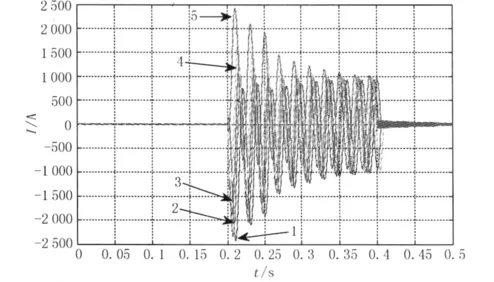
图7 零序电流与电源初始相角的关系

图7说明电源的初始相角影响零序电流的首次过零时间，对于α=0°到180°，随着初始相角的增大，零序电流的首次过零时间变短。α=0°和180°时对开断短路电流最苛刻。

4.2 变压器时间常数τ对ih的影响

变压器的时间常数由绕组的电阻和漏感决定，对变压器来说，它们是固定的，但却可以影响零序电流。表1给出了变压器时间常数与ih峰值的关系，由表1可见，电流峰值随时间常数的增大而增加。当τ≤0.2 ms时，电流突然增到无限大，因此在设计变压器时要注意避免出现此类参数。

表1 变压器时间常数与ih峰值的关系 kA

4.3 短路点位置对ih的影响

短路点的位置决定系统的正序、负序、零序等值阻抗。对于1号线，计算单相短路故障点距变电站距离分别为6 m、10 m、15 m、20 m、26 m时，变压器角接绕组中零序电流的最大值，图8给出了它们之间的关系。由图8可以看出，ih峰值与短路点位置呈现抛物线特性，在变压器出口处和电源出口处短路时，短路电流很大，在电源出口处发生短路，短路电流最大。在线路中间发生短路时，短路电流最小。

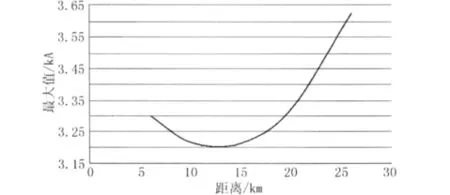
图8 零序电流与故障点位置的关系

5 结论

a． ih与一次侧零序电流具有相似性，出现了零点漂移。当接地短路消失时，会引起包含多种频率成分的暂态振荡，容易对绕组的绝缘造成损害。

b． α =0°(60°)和 α =180°(120°)时 ih相对于时间轴对称，对于α=0°到180°，随着初始相角的增大，零序电流的首次过零时间变短。

c． ih峰值随变压器时间常数的增大而增加。当τ≤0.2 ms时，电流突然增到无限大，在设计变压器时要注意避免出现此类参数。

d． 在电源出口处发生短路，ih峰值最大，而在线路中间发生短路，短路电流最小。ih峰值与短路点位置呈现抛物线特性。

［1］ 蒋 伟，吴广宁，黄 震，等．短路故障对部分接地方式下220 kV变压器影响分析 ［J］．电力系统自动化，2007，31(21):98－101．

［2］ 谢毓城．电力变压器手册 ［M］．北京:机械工业出版社，2003．

［3］ 祝瑞金，胡 宏，曹 路．基于人工单相接地短路试验的电力系统计算用模型参数校核方法研究［J］．电网技术，2007，31(5):58－63．

［4］ 毕大强，梁武星，柴建云，等．变压器三角形绕组中环流的构造方法 ［J］．电力系统自动化，2008，32(1):39－43．

［5］ 袁宇波，陆于平，陈久林，等．变压器三角形侧零序环流助增对差动保护的影响 ［J］．电力系统自动化，2006，30(3):44－50．

［6］ 索南加乐，焦在滨，宋国兵，等．一种适用于Y/△接线变压器的励磁电感计算方法 ［J］．电力系统自动化，2007，31(9):32－36．

［7］ 陆国庆，姜新宇，江 健，等．110 kV及220 kV系统变压器中性点经小电抗接地方式的研究及其应用 ［J］．电网技术，2006，30(1):70－74．

［8］ 蒋陶宁，李 军，孙成秋，等．交流特高压输电线路复杂地线系统单相短路电流的计算 ［J］．电网技术，2011，31(5):16－21．

［9］ 辜承林，陈乔夫，熊永前．电机学［M］．武汉:华中科技大学出版社，2007．

［10］ 李光琦．电力系统暂态分析 ［M］．北京:中国电力出版社，2011．

［11］ 林福昌．高电压工程［M］．北京:中国电力出版社，2007．

［12］ 邱关源．电路 ［M］．北京:高等教育出版社，2005．

［13］ 林 莘，李 爽，徐建源，等．考虑GIS外壳传输特性的VFTO计算模型［J］．电网技术，2010，34(11):203－207．

［14］ 曾昭华，林集明，班连庚，等．特快速暂态过电压及研究实例 ［J］．电网技术，1996，20(3):5－10．

［15］ 陈庆国，张乔根，邱毓昌，等．GIS在快速暂态过电压下的放电特性 ［J］．电网技术，2000，24(9):1－4．

［16］ 衣立东，吕世荣．750 kV输变电示范工程施工关键技术的研究与应用［J］．电网技术，2006，30(3):51－56．

［17］ 林 莘，李 爽，徐建源．特高压GIS壳体过电压特性［J］．沈阳工业大学学报，2009，31(6):606－610．