带时间窗车辆路径问题的多目标文化基因算法*
王 君
(天津财经大学商学院,天津300222)
1 引言
随着顾客对物流配送要求的提高,带时间窗的车辆路径问题VRPTW(Vehicle Routing Problem with Time Windows)一直是物流与供应链管理的热点问题。VRPTW是典型的组合优化问题,主要采用启发式优化算法进行求解。启发式算法分为以禁忌搜索TS(Tabu Search)[1]为代表的局部搜索和以遗传算法GA(Genetic Algorithm)[2]为代表的种群搜索两大类。现在更加趋向于多种搜索机制的结合,以弥补单一启发式算法的不足。
文化基因算法MA(Memetic Algorithm)是以文化进化思想为指导的智能优化算法,用局部搜索来模拟文化进化过程,既具有群体算法搜索范围大的优点,又具有局部算法搜索的深度优势[3],目前已经出现了用MA求解车辆路径问题的研究[4]。多目标文化基因算法MOMA(Multi-Objective MA)是采用多目标优化机制的MA算法,已经成功应用到车间调度[5]、物流网络设计[6]、飞机航线调度[7]等多目标优化问题中。
VRPTW需要同时考虑车辆的使用数和车辆行驶距离两个目标,因此它也是一个多目标优化问题,现有研究大部分采用多目标进化算法求Pareto最优解集[8,9],然而用MOMA解决VRPTW的研究十分罕见。本文基于以上研究成果,提出求解VRPTW的一种MOMA算法,运用不同的适应度函数分别支持种群和局部精英解的选择。对国际通用的benchmark数据进行仿真对比实验,表明本文提出的MOMA算法是求解VRPTW问题的有效方法。
2 问题描述与数学模型
一个VRPTW描述为:设G={I,E}为一个完备的无向图,其中,I={0,1,2,…,n}为节点集;E={i,j}为边集,i,j∈I且i≠j。0代表车库点,其余为顾客点,一队具有相同装载能力的车辆从车库点出发,实现对所有顾客点的配送服务,最终回到车库。每个顾客点有一个固定的需求和固定的服务时间,并且只能由一辆车服务。车辆必须在时间窗内到达顾客点,且不能晚于结束时间;如果车辆到达时间早于顾客规定的时间窗开始时间,那么车辆需要等待。优化目标是确定车辆的行驶路线,在满足顾客要求的前提下,使得总费用最小。
为描述方便,定义如下的标号和参数变量:
cij:表示节点i和节点j间的距离;
V:表示车辆集合;
tij、ati、wti、sti:分别表示车辆从节点i到节点j的行驶时间、到达节点i的时间、在服务节点i前的等待时间和服务节点i的持续服务时间;
[Ei,Li]:节点i的时间窗,最早和最迟开始服务时间;
di:表示第i个顾客的配送货物量;
Qv:车辆v的载重量;
xijv:是0-1类型的决策变量,即:
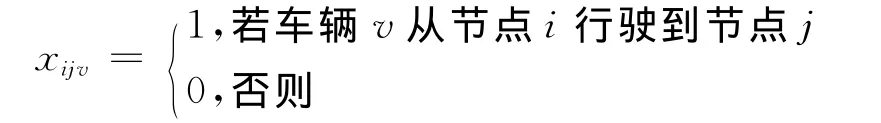
那么,VRPTW的数学模型为:

满足以下条件:
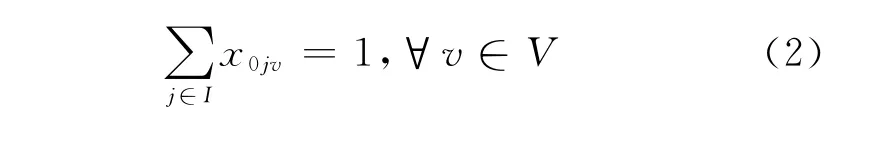

其中,式(1)表示目标函数,同时最小化使用车辆数和车辆行驶总路径长度两个目标。式(2)和式(3)表示每辆车都要从车库出发,最终回到车库。式(4)和式(5)表示每个顾客有且仅有一辆车为其服务。式(6)表示运货量不能超过车辆的载重量。式(7)、式(8)分别是车辆在节点i的等待时间、到达节点j的时间的计算公式,其中wt0=0,at0=0,st0=0。式(9)是时间窗约束,即顾客到达节点i的时间需在时间窗关闭之前。式(10)指决策变量是0-1变量。
3 多目标文化基因算法
3.1 精英解的存储和选择机制
MOMA算法是基于种群的全局搜索和基于个体的局部搜索的结合,因此首先要解决的是如何协调种群搜索和局部搜索得到的Pareto非占优解的相互关系。如图1所示,对父代种群经过交叉操作得到的每个新个体进行局部搜索,搜索得到的局部最优解作为子代的个体。采用一个容量足够大的存储池结构来存储局部搜索得到的Pareto非占优解。比较存储池中的解集,如果在局部搜索过程中得到了新的Pareto非占优解,那么就用其更新存储池中的一个劣解。局部搜索完成后,对父代种群、子代种群和存储池中的所有解采用基于Pareto排序和拥挤度的选择机制[10]进行选择操作,得到新的父代种群,然后进行新的一次迭代过程。
3.2 适应度函数
因为种群搜索和局部搜索的机制不同,所以在同时考虑个体的两个目标函数时,采用两种不同的适应度函数,分别应用于对种群的选择操作和对局部搜索的最优解选择操作。

Figure 1 Diagram of elite solutions storage and coordination mechanism图1 精英解的存储和协调机制示意图
种群的选择操作采用基于Pareto排序和拥挤度的度量方法[10],即:
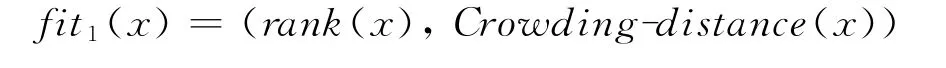
其中,第一项rank(x)表示Pareto占优的层级关系,rank(x)<rank(y)表示解x占优y。第二项Crowding-distance(x)是拥挤距离,描述了在同一rank中x与相邻两个解的距离,距离越大表示该解越好。在进行选择操作时,对父代种群、子代种群和存储池中的所有解按照第一关键字是rank升序、第二关键字是Crowding-distance降序的方式进行排序,然后选择前N个(N为种群规模200)个体进入下一代。
在局部搜索过程中,每次都要从候选的邻域解列表中选择一个最好的解来更新当前解,然后继续搜索其邻域,因此可以引入Pareto强度的概念来定义局部搜索运用的适应度函数[11]。
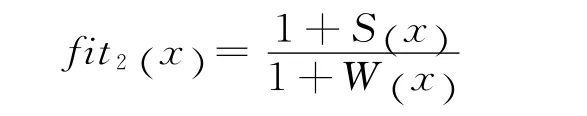
其中,S(x)是在存储池中被x占优的解的个数,W(x)是在存储池中占优x的解的个数。局部适应度函数反映了解x在解集中Pareto占优关系的强弱程度,若x强度大,则适应度高,表明x在解集中处于优势地位,可以在局部搜索过程中优先搜索处于优势地位解的邻域。
3.3 染色体编码方式、初始种群的生成及交叉算子
MOMA算法采用车辆行驶路径顺序的自然数编码方式。用自然数表示顾客;0表示车库,用来区分不同车辆的行驶路径。假如,三辆车的行驶路径分别为(1→2→3)、(4→5)和(6→7→8),车库中有五辆车,则染色体编码为(0,1,2,3,0,4,5,0,6,7,8,0,0)。
采用随机车辆配载方法生成初始种群个体,每个个体对应一个可行解。具体方法为:首选,对顾客按照时间窗结束时间Li由早到晚排序得到顾客序列,根据载重量和时间窗估计每辆车服务顾客的数量N*;然后,在顾客序列中以大致等长的间隔随机抽取N*个顾客组成一条路径,并保证满足时间窗和载重量约束。要求间隔的选择具有一定的随机性,这样就可以生成不同的初始解。
交叉算子采用Ombuki等[8]的方法,随机选择两个父代染色体P1、P2,每个染色体随机选取一辆车所服务的顾客序列作为交叉信息,记为…和s…,然后把…从P1中移除,应用插入可行邻域[12],再依次把…插回到P1中,得到子代个体。同样,把s…先从P中移除再2依次插回,得到另一个子代个体。
3.4 局部禁忌搜索机制
利用插入可行邻域和2-Opt可行邻域[12]两种邻域结构,对父代种群交叉操作后得到的中间种群进行禁忌搜索,邻域结构采取随机选择的策略。插入可行邻域的禁忌对象设置为邻域类型以及插入的顾客和插入点的紧后顾客组成的顾客对;2-Opt可行邻域的禁忌对象设置为邻域类型以及两个路径断点的紧后顾客组成的顾客对。禁忌长度设置最小值LMINTA和最大值LMAXTA,在局部搜索中禁忌长度由最小值均匀地增大到最大值。藐视准则为若禁忌对象对应的适应度函数fit2(x)优于最好解,则无视其禁忌属性而仍采纳其为当前选择。设置两种停止规则:一种是设置一个最大迭代数IMTA;另一种是在INMTA(INMTA<IMTA)次迭代内所发现的最好解无法改进,即停止局部搜索。
3.5 算法总体流程
MOMA结合了种群搜索和个体搜索,选择不同的进化操作和局部搜索策略构成不同的MOMA。本文选择对初始种群和进行交叉操作后得到的子代种群进行局部搜索,MOMA的具体流程如算法1的伪代码所示。


4 仿真实验
测试采用Solomon的r1和rc1两类benchmark数据(数据来自http://web.cba.neu.edu/~msolomon/problems.htm),r类数据集节点的地理位置为随机生成,rc类数据集的每个算例的一部分顾客需求是随机生成,另一部分顾客需求在地理位置或者服务时间窗上具有聚集特征。算法用VC++6.0编程实现,在Intel Pentium Dual T2410 CPU 2 GHz、1 GB内存、Windows XP SP3的主机上运行。
与不带局部搜索的多目标算法NSGA-Ⅱ和线性加权的单目标MA算法进行对比实验,以验证本文提出的MOMA算法的有效性。经多次反复实验设置MOMA算法的参数为:种群规模200,进化代数80,候选解数目300,LMINTA=5,LMAXTA=20,IMTA=1000,INMTA=100。MA采取顺序优化的方式,首先优化车辆使用数目标,然后优化车辆行驶总路径长度,可以加权目标函数为min(1000f1+f2),并作为个体的适应度,在种群选择过程中选取适应度小的个体进入下一代。
NSGA-Ⅱ参数为:进化代数800,变异算子为2-Opt可行邻域,变异概率0.2,其余参数和MOMA相同。GA较MA选择较大的进化代数是考虑了收敛效果和计算耗时两个因素。每个算例均独立运行10次,记录最好解。性能对比结果如表1所示,每个解包括使用的车辆数nv、总路径长度和平均运行时间。对比三种算法的求解结果,用加粗的字体显示了较好的解和较快的求解时间。
从计算耗时来看,NSGA-Ⅱ、MA和MOMA呈递增趋势,这是因为局部禁忌搜索需要在个体的基础上搜索大量的邻域结构,从而增加了程序的运行时间,而基于Pareto的排序又增加了MOMA的运算时间。但是,从求解质量上看,MA和MOMA都要明显优于NSGA-Ⅱ,说明局部搜索策略可以显著提高算法的寻优能力。比较MA和MOMA,有10个算例双方都得到了唯一解。这10个算例中MA和MOMA各有5个解要好于对方,说明基于Pareto的优化方式在求解有唯一最优解的情况时不差于线性加权的方法,鲁棒性较好。在其余的10个算例中,MOMA都得到了多个解,其中有7个算例MOMA得到的Pareto最优解都要好于MA,有2个算例(r102和r109)MA得到的最优解好于MOMA的某个最优解,而只有1个算例(rc101)MA得到的最优解好于MOMA得到的所有Pareto最优解,说明MOMA求解多目标问题时具有很大的优势。
5 结束语
本文提出了求解VRPTW问题的多目标文化基因算法,种群搜索采用遗传算法的进化模式,局部搜索采用禁忌搜索机制。种群的选择操作采用基于Pareto排序和拥挤度的度量方法来定义适应度函数,局部搜索采用Pareto强度来定义适应度函数。对比实验结果表明,带局部搜索机制的
MOMA明显优于不带局部搜索的NSGA-Ⅱ,而且
MOMA的多目标机制对优化最优解唯一的问题具有鲁棒性,是求解VRPTW问题的一种有效的多目标优化算法。这对研究其他类型的车辆路径问题和多目标优化方法提供了一定的参考。
[1] Gendreau M,Hertz A,Laporte G.A tabu search heuristic for the vehicle routing problem[J].Management Science,1994,40(10):1276-1290.
[2] Chen Sen,Jiang Jiang,Chen Ying-wu,et al.A class of nondeterministic vehicle routing problem model and its algorithm design[J].Computer Engineering,2011,37(14):186-188.(in Chinese)
[3] Krasnogor N,Smith J.A tutorial for competent memetic algorithms:Model,taxonomy,and design issues[J].IEEE Transactions on Evolutionary Computation,2005,9(5):474-488.
[4] Labadi N,Prins C,Reghioui M.A memetic algorithm for the vehicle routing problem with time windows[J].Rairo-Operations Research,2008,42(3):415-431.
[5] Qian B,Wang L,Huang D-X,et al.Scheduling multi-objective job shops using a memetic algorithm based on differential evolution[J].International Journal of Advanced Manufacturing Technology,2008,35(9-10):1014-1027.

Table 1 Experimental results表1 程序运行结果
[6] Pishvaee M S,Farahani R Z,Dullaert W.A memetic algorithm for bi-objective integrated forward/reverse logistics network design[J].Computers &Operations Research,2010,37(6):1100-1112.
[7] Burke E K,de Causmaecker P,de Maere G,et al.A multiobjective approach for robust airline scheduling[J].Computers &Operations Research,2010,37(5):822-832.
[8] Ombuki B,Ross B J,Hanshar F.Multi-objective genetic al-gorithms for vehicle routing problem with time windows[J].Applied Intelligence,2006,24(1):17-30.
[9] Jozefowiez N,Semet F,Talbi E G.An evolutionary algorithm for the vehicle routing problem with route balancing[J].European Journal of Operational Research,2009,195(3):761-769.
[10] Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[11] Carcangiu S,Fanni A,Montisci A.Multiobjective tabu search algorithms for optimal design of electromagnetic devices[J].IEEE Transactions on Magnetics,2008,44(6):970-973.
[12] Wang Jun,Li Bo.Multi-objective tabu search algorithm for vehicle routing problem with fuzzy due-time[J].Computer Integrated Manufacturing Systems,2011,17(4):858-866.(in Chinese)
附中文参考文献:
[2] 陈森,姜江,陈英武,等.一类非确定性车辆路径问题模型及其算法设计[J].计算机工程,2011,37(14):186-188.
[12] 王君,李波.带模糊预约时间的车辆路径问题的多目标禁忌搜索算法[J].计算机集成制造系统,2011,17(4):858-866.

