关联规则挖掘模型在大学生评价中的应用*

高晓红，刘 鹏

(楚雄师范学院数学系，云南 楚雄 675000)

1 引言

随着信息化时代的来临及网络和计算机应用的迅速普及，近几年各高校收集了学生的大量信息，并形成了一定的信息数据库。在学生队伍建设中，面对如此海量的信息，学校管理者如何发现具有实际指导意义的规律，特别是如何才能在选拔人才时综合考虑学生的实际能力，将成为研究热点。关联规则挖掘是数据挖掘的一个重要研究分支，其主要研究目的是从大型数据集中发现隐藏的、有价值的属性间存在的规律。本文用关联规则挖掘技术在这方面做了一定的探索和研究，期望能得到一些有益的启示。

2 相关概念

2.1 关联规则的基本原理

设I={i1，i2，…，in}是项的集合。包含K个项的项集称作K项集。设D是数据库记录的集合，其中每个事务T是项的集合，且T⊆I。设X是一个项集，事务T包含X，当且仅当X⊆T。

关联规则是形如X⇒Y的蕴涵式，这里X⊂I，Y⊂I，且X∩Y=φ。X称为规则的左部或规则的前提(简记LHS)，Y称为规则的右部或结论(简记RHS)。

度量规则的参数是支持度(Support)与置信度(Confidence)。支持度是指数据集中的实例同时包含条件属性与决策属性的共同概率，支持度揭示了规则的重要性。置信度表示实例在包含条件属性的前提下，也包含决策属性的条件概率，它揭示了规则的可信度。在粗糙集理论中支持度与置信度可以表示为:

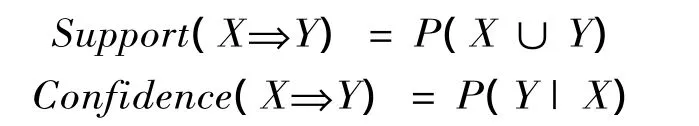
其中P(X)表示X在D中出现的概率，其余相似。Support(X⇒Y)指X、Y在D中同时出现的概率;Confidence(X⇒Y)表示在X出现的前提下Y出现的概率［1］。若得到的规则同时满足支持度不小于支持度阈值和置信度不小于置信度阈值，则该规则有意义［2］。

2.2 决策表的属性约简

在决策表中，不同的属性可能具有不同的重要性。要找出某些属性的重要性，就要从表中去掉一些属性，再来考察没有该属性后分类会有怎样的变化。若去掉该属性后分类变化较大，则说明该属性强度较大，重要性高;反之，则说明该属性重要性低。决策表的一般属性约简的具体步骤是:

(1)求多个条件属性 C1，C2，C3，…，Cn的等价类;

(2)计算从C中分别去掉C1，C2，C3，…和Cn后所有属性集下的等价类;

(3)求决策属性D与条件属性C的依赖度;

(4)检查从C中去掉C1，C2，C3，…和Cn时分类的变化情况，若分类发生较大变化，说明该属性不可去，否则可去。

3 关联规则挖掘模型

在大量实践的基础上，人们总结出了一个相对成熟的基于粗糙集的关联规则挖掘模型，其基本思想和步骤见图1。

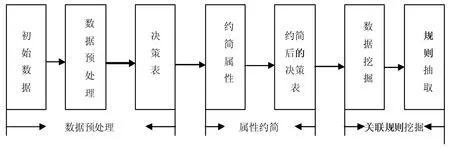
图1 基于粗糙集的关联规则模型

本文将基于粗糙集的关联规则的挖掘过程分为三步:数据预处理，属性约简与关联规则挖掘。

(1)数据预处理:通过对高校学生数据的初始信息进行数据清洗，缺失值处理，转换及数据选择，获取初始信息表，且将初始表转换为决策表形式，并明确条件属性集和决策属性;

(2)属性约简:对条件属性进行约简，删除多余属性，在此基础上利用一般属性约简算法进行属性约简并生成约简属性集;

(3)关联规则挖掘:输入支持度阈值和置信度阈值，根据数据约简结果，利用粗糙集理论文献［3］中的算法，进行关联规则的挖掘。

4 关联规则挖掘模型在大学生评价中的应用

本文以楚雄师院数学系学生信息为例(根据学生的智育成绩、综合成绩、证书总数等来评价学生的等级)，说明基于粗糙集的关联规则挖掘模型的实施过程。

根据上述构建的数据挖掘模型，利用属性约简算法对大学生数据进行约简。首先进行数据项处理，其次求出约简或近似约简，最后提取规则，可将其应用于新对象的分析和预测［4］。

4.1 数据预处理

用基于粗糙集的数据挖掘方法进行知识挖掘，需要获取数据表。本文以楚雄师院数学系部分学生信息为例，采用关系数据库模型，经关系数据库的导入及连接进行抽象﹑离散化等预处理。将影响学生评价的因素:生源地，家庭背景，政治面貌，高考成绩，毕业学校，学习程度，大学期间学生的智育平均成绩，大学期间学生综合平均成绩，英语水平，计算机水平，获奖证书总数作为系统的条件属性C，而将对学生的评价等级作为决策属性D。

对于具体的数据处理时可先将其抽象、离散化、使后续的表格简洁明了。生源地(a:云南省内 b:云南省外)，家庭背景(a:好 b:一般 c:差)，政治面貌(a:正式党员 b:预备党员

c:团员)，高考成绩(a:490－495分 b:496－500分 c:501－505分 d:506－510分 e:510分以上)，毕业学校(a:普通高中 b:重点高中 c:其它)，学习程度(a:努力 b:一般

c:不努力)，平均智育(a:0－75分 b:76－80分 c:81－85分 d:86－100分)，平均综合(a:0－75分 b:76－80分 c:81－85分 d:86－100分)，英语水平(a:通过四级 b:未通过四级)，计算机水平(a:国家二级 b:国家三级 c:国家四级 d:无)，证书总数(a:0－5b:6－10c:11－15d:15以上)，学生评价等级(a:优 b:良 c:中 d:差)。

注:划分等级的依据为学生的平均智育成绩、平均综合成绩和证书总数，若同时满足平均智育成绩在81－100分之间，平均综合成绩在81－100分之间和证书总数大于等于11个，则对该生的评价为优;若同时满足平均智育成绩在76－80分之间，平均综合成绩在76－80分之间和证书总数为6－10个，则对该生的评价为良;若满足平均智育成绩小于等于75分，或平均综合成绩小于等于75分，或证书总数小于等于5个，则对该生的评价为中;若同时满足平均智育成绩小于等于75分，平均综合成绩小于等于75分和证书总数小于等于5个，则对该生的评价为差。

对30个初始数据进行简单整理和离散化﹐将其再进行预处理(即数据清洗、转换和选择)后可得表1，如下所示。

表1 预处理后的大学生数据

4.2 属性约简

为了计算方便，用C1，C2，C3，C4，C5，C6，C7，C8，C9，C10，C11来表示条件属性，其中 C1={生源地}，C2={家庭背景}，C3={政治面貌}，C4={高考成绩}，C5={毕业学校}，C6={学习程度}，C7={平均智育}，C8={平均综合}，C9={英语水平}，C10={计算机水平}，C11={证书总数}，D表示决策属性，且D={评价等级}。通过一般属性约简方法对表1进行约简，具体过程如下:

由以上计算可知，C1，C2，C3，C4，C6，C9对D的依赖度为0，即它们在D中是不必要的，为冗余属性，将它们删除。因此 C 的属性约简集为{C5，C7，C8，C10，C11}，即 C={毕业学校，平均智育，平均综合，计算机水平，证书总数}。对属性约简后对应的表再次删除冗余对象，由于对象6、20与对象5重复，对象8、10、11与对象7重复，对象14、22与对象12重复，对象15与对象9重复，重复对象中保留一个即可，不妨保留对象5、7、9、12。于是，得到属性约简后的最终数据表，如表2所示。

表2 约简后的数据表

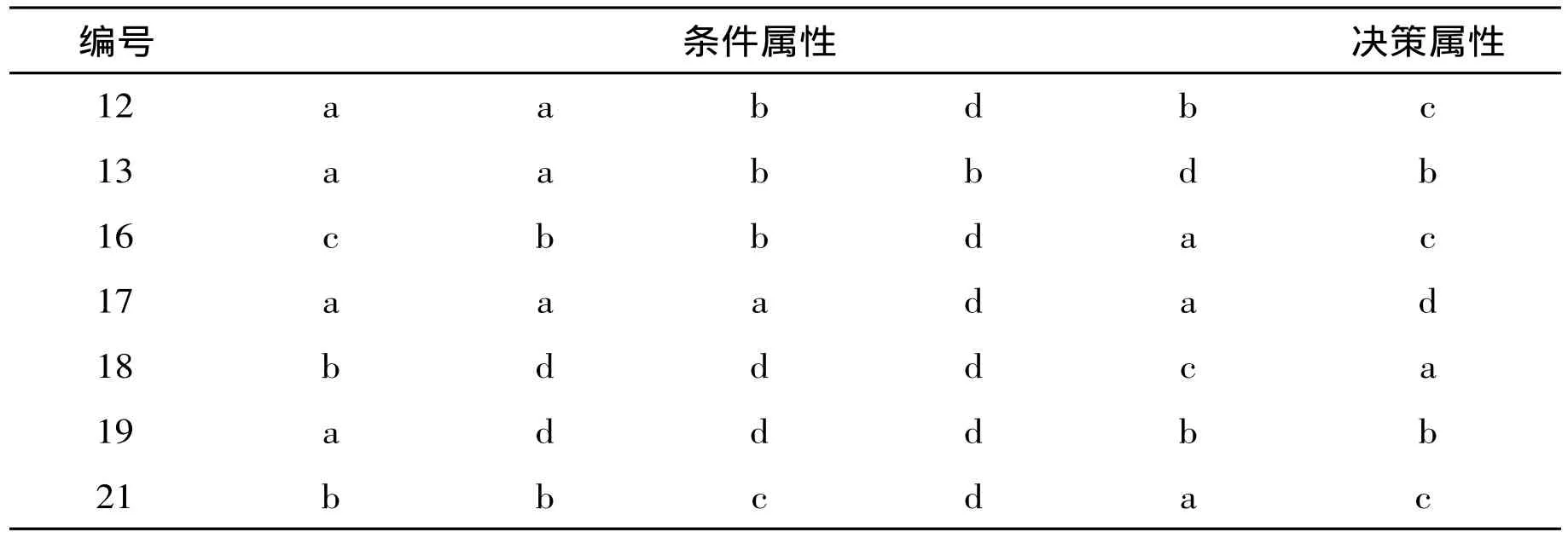
12 a a b d b c 13 a a b b d b 16 c b b d a c 17 a a a d a d 18 b d d d c a 19 a d d d b b 21 b b c d a c

再求表2条件属性对于决策属性的重要性，计算过程如下:

由以上计算可知:条件属性C5，C7，C8，C10，C11对于决策属性D都是很重要的，不可删除，且有σCD(C7)＞σCD(C11)＞σCD(C8)=σCD(C5)＞σCD(C10))，即在学生评价中，各属性对学生的重要性从大到小依次为:平均智育、证书总数、平均综合、毕业学校、计算机水平。其中σCD(Ci)表示条件属性集C中的属性Ci对决策属性D的重要性。

4.3 关联规则挖掘

给出支持度阈值为5%，置信度阈值为80%，根据表2得到的约简，将属性之间的隐含关系进行关联规则挖掘［5］，得到一些有意义的规则。

Rule1:if(毕业学校 =a)and(平均智育 =c)，then(学生评价 =a)，该规则置信度为100%，支持度为2/14=14.3%;

Rule2:if(毕业学校 =b)and(平均智育 =a)and(平均综合 =c)and(计算机水平 =d)and(证书总数 =c)，then(学生评价 =b)，该规则置信度为100%，支持度为1/14=7.1%;

Rule3:if(毕业学校 =a)and(平均智育 =b)，then(学生评价 =b)，该规则置信度为100%，支持度为2/14=14.3%;

Rule4:if(毕业学校 =b)and(平均智育 =b)and(平均综合 =b)and(计算机水平 =d)and(证书总数 =b)，then(学生评价 =b)，该规则置信度为100%，支持度为1/14=7.1%;

Rule5:if(毕业学校 =a)and(平均智育 =a)and(平均综合 =b)and(计算机水平 =d)then(学生评价 =c)，该规则置信度为100%，支持度为2/14=14.3%;

Rule6:if(毕业学校 =a)and(平均智育 =a)and(平均综合 =b)and(计算机水平 =b)and(证书总数 =d)，then(学生评价 =b)，该规则置信度为100%，支持度为1/14=7.1%;

Rule7:if(毕业学校 =c)and(平均智育 =b)and(平均综合 =b)and(计算机水平 =d)and(证书总数 =a)，then(学生评价 =c)，该规则置信度为100%，支持度为1/14=7.1%.

Rule8:if(毕业学校 =a)and(平均智育 =a)and(平均综合 =a)and(计算机水平 =d)and(证书总数 =a)，then(学生评价 =d)，该规则置信度为100%，支持度为1/14=7.1%;

Rule9:if(毕业学校 =b)and(平均智育 =d)and(平均综合 =d)and(计算机水平 =d)and(证书总数 =c)，then(学生评价 =a)，该规则置信度为100%，支持度为1/14=7.1%;

Rule10:if(毕业学校 =a)and(平均智育 =d)and(平均综合 =d)and(计算机水平 =d)and(证书总数 =b)，then(学生评价 =b)，该规则置信度为100%，支持度为1/14=7.1%;

Rule11:if(毕业学校 =b)and(平均智育 =b)and(平均综合 =c)and(计算机水平 =d)and(证书总数 =a)，then(学生评价 =c)，该规则置信度为100%，支持度为1/14=7.1%;

于是，上述规则均同时满足支持度不小于支持度阈值和置信度不小于置信度阈值，故以上11条规则都是有意义的。上述规则的含义如下:

由Rule1知:毕业学校为普通高中，平均智育成绩在81－85分之间，则对该学生的评价为优;由Rule2知:毕业学校为重点高中，平均智育成绩在0－75分之间，平均综合成绩在81－85分之间，无计算机证书，证书总数为11－15个，则对该学生的评价为良;由Rule3知:毕业学校为普通高中，平均智育成绩在76－80分之间，则对该学生的评价为良;由Rule4知:毕业学校为重点高中，平均智育成绩在76－80分之间，平均综合成绩在76－80分之间，无计算机证书，证书总数为6－10个，则对该学生的评价为良;由Rule5知:毕业学校为普通高中，平均智育成绩在0－75分之间，平均综合成绩在76－80分之间，无计算机证书，则对该学生的评价为中;由Rule6知:毕业学校为普通高中，平均智育成绩在0－75分之间，平均综合成绩在76－80分之间，获得计算机三级证书，证书总数为15个以上，则对该学生的评价为良;由Rule7知:毕业学校为其它，平均智育成绩在76－80分之间，平均综合成绩在76－80分之间，无计算机证书，证书总数小于等于5个，则对该学生的评价为中;由Rule8知:毕业学校为普通高中，平均智育成绩在0－75分之间，平均综合成绩在0－75分之间，无计算机证书，证书总数小于等于5个，则对该学生的评价为差;由Rule9知:毕业学校为重点高中，平均智育成绩在85分以上，平均综合成绩在85分以上，无计算机证书，证书总数为11－15个，则对该学生的评价为优;由Rule10知:毕业学校为普通高中，平均智育成绩在85分以上，平均综合成绩在85分以上，无计算机证书，证书总数为6－10个，则对该学生的评价为良;由Rule11知:毕业学校为重点高中，平均智育成绩在76－80分之间，平均综合成绩在81－85分之间，无计算机证书，证书总数小于等于5个，则对该学生的评价为中。

从以上规则可知，毕业学校，平均智育成绩，平均综合成绩，计算机等级证书及证书总数对学生的评价具有显著的影响。因此，建议社会各阶层在选拔人才时，改变传统的只看学历和毕业学校的观念，需多考虑以上因素，防止人才被埋没的现象，从而减少不必要的损失。

5 结论

本文在对数据挖掘相关技术、关联规则挖掘算法进行深入研究的基础上，归纳总结了基于粗糙集理论的关联规则挖掘模型和属性约简算法，利用楚雄师院数学系学生的数据，进行了关联规则的挖掘实验，并将其成功应用于大学生评价中，并对关联规则产生的结果进行了解释，为社会选拔人才提供有价值的参考。

［1］David Hand，Heiki Mannila，Padhraic Smith.Principles of Data Mining.机械工业出版社，中信出版社，2003.

［2］姜云苹，葛世伦，蒋家尚，王丽敏.基于粗糙集理论的关联规则挖掘在教师成长中的应用 ［J］.计算机与信息技术，2008，(01):57—58.

［3］白秀玲，崔林，王向阳.一种基于关联规则挖掘的粗糙集约简算法 ［J］.计算机工程与应用，2003，39(10):185—186.

［4］曾黄麟.基于粗集方法的智能专家系统 ［J］.中国工程科学，2001， (02):47—50.

［5］Han Jiawei Lamber M.数据挖掘概念与技术 ［M］.北京:机械工业出版社，2006:56—76.