用自制圆锥摆与Spss标定重力加速度*

吉明荣，王新春，王昆林，司民真

(楚雄师范学院物理与电子科学系，云南 楚雄 675000)

引言

目前，大学物理实验中测量重力加速的方法一般用单摆法及改进［1］、落球法及改进［2］、智能系统［3］等。单摆法由于极易受到空气阻尼的影响使得周期会衰减，对实验中摆球的起始状态很难控制，对周期的测量必然会产生很大的偏差，最终会导致实验结果变差;落球法误差主要来源于挡光片宽度及计时系统，不可避免;智能型系统测重力加速度，系统较为复杂，且不利于训练学生的实验能力。通过自制圆锥摆系统，用直流稳压电源提供小球做圆锥摆的稳恒能量，可明显减弱空气阻尼、刀口磨损等因素的影响，用光电门精确地测出圆锥摆振动周期，采用自制带千分头的测高探头测出摆球处于动态的高度。引入计算机辅助分析 (Spss)软件［4］的方法，可显著减小因仪器或人为因素 (人工作图)带来的误差，能得到更为准确的实验结果。

1 实验仪器

1.1 实验装置

自制圆锥摆实验系统装置如图1所示，主要由三角支架、直流稳压电源(YB1733A2A)、记时记数测速仪 (QF－MUJ58)、变速电机 (5－12V)、联轴器、小钢球(20g)、光电门及支架、测高探头组成。

1.2 仪器安装及调试

如图1所示，用螺钮将变速电机固定在高约70cm重约15kg铁制支架上，将质量约为20g的钢球用细线与电机上的联轴器固定好。直流电源用于驱动电机，记时记数测速仪用来测定周期，用测高探头测定摆球高度。调节支架水平泡，使支架上的联轴器与电机保持平面水平;直流电源一般控制在6V—7V范围内，可保证摆球做平稳圆锥摆动，可显著减弱滞后现象，从而可忽略空气阻力造成的影响;调整测高探头千分尺读取小球动态高度;起动电机的同时应给予小球一个合适的初速度，使小球能尽快进入平稳的圆周摆群运动状态。

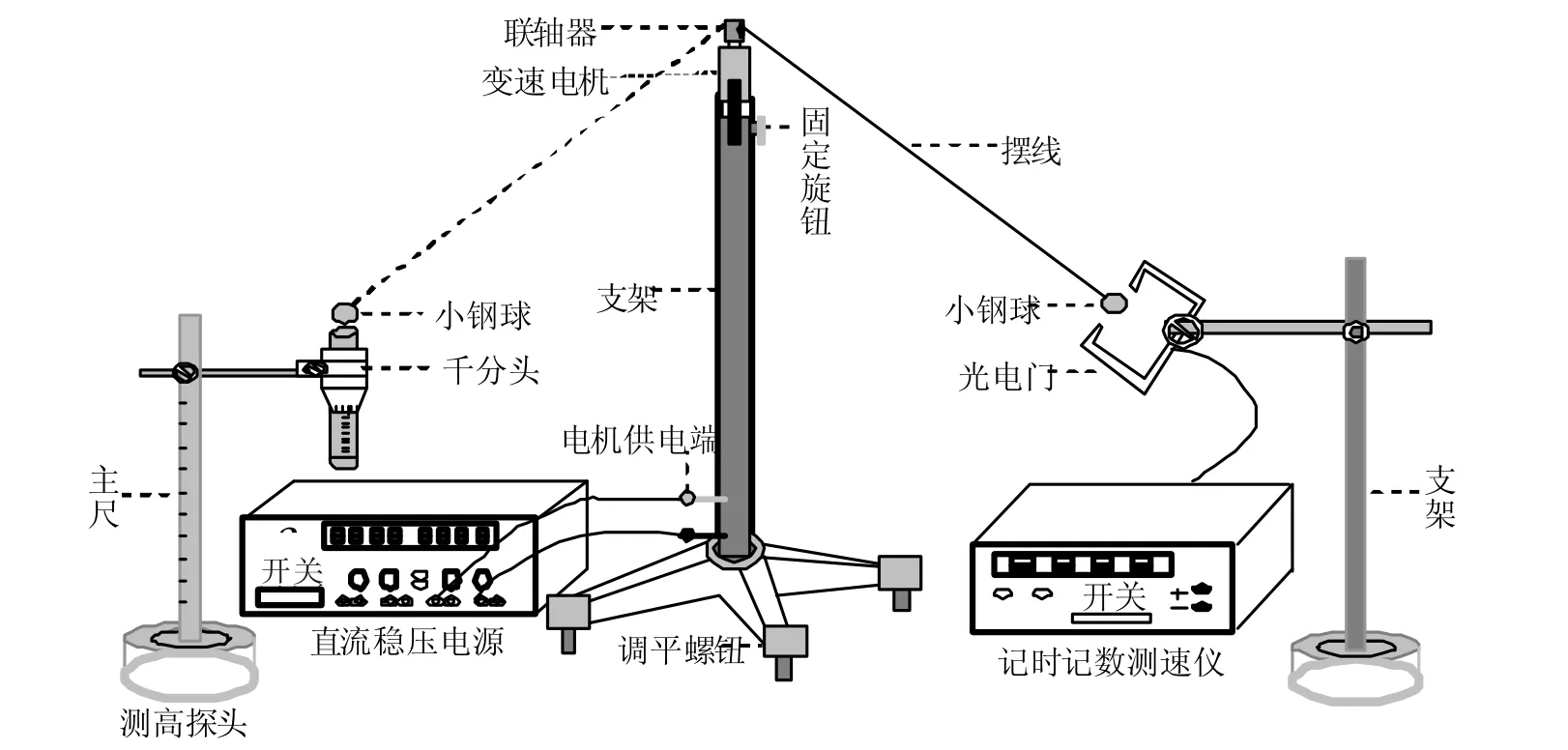
图1 实验装置简图

2 实验原理

2.1 测量原理

实验原理图如图2所示，在电机的驱动下，质量为m的小球作平稳的圆锥摆运动，摆角为θ，L为摆长，d1、d2、R 分别为小球、联轴器、小球做圆周运动的半径，H2、h1分别悬点、小球下边缘与桌面的高度。由此小球质心与桌面的高度为 H1=h1+d1/2。而且:sin θ=

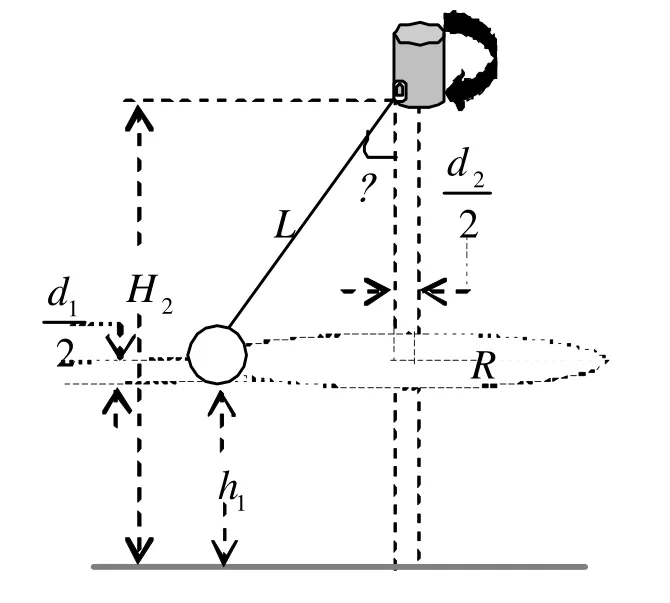
图2 实验原理图

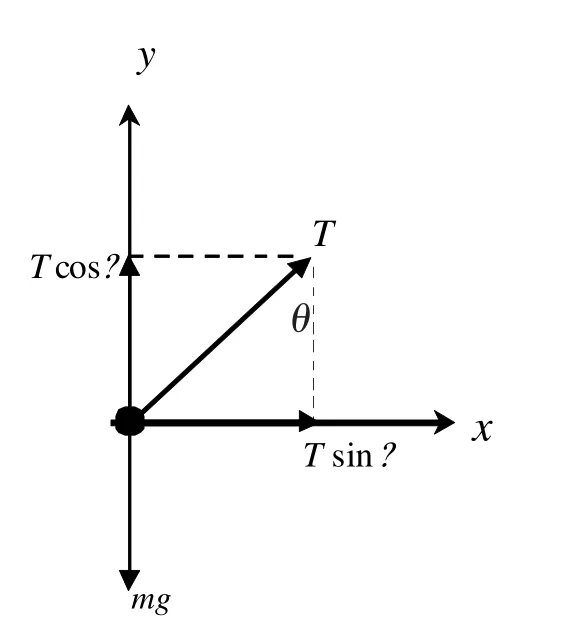
图3 小钢球受力分析图

由图3受力分析可得

由(1)、(2)可得

由图2 中 sin θ、tan θ 的表达式可得

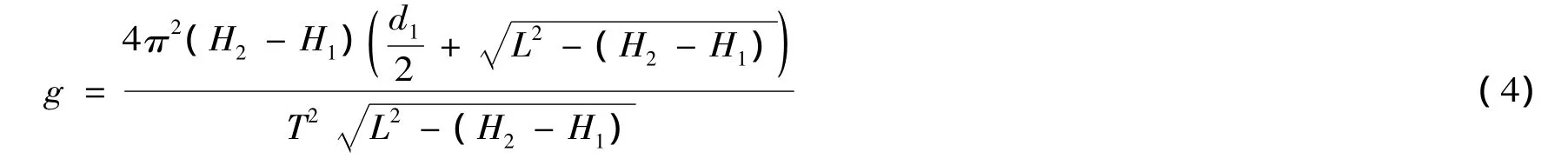
用直流稳压电源驱动调速电机，使小钢球作圆锥摆运动，通过对其周期测量，各长度的综合量的测量，应用Spss线性估计功能，分析长度综合量(Ai)与周期的平方(T2i)的线性关系，从而可以标定出重力加速度g，并对其不确定度做出估算。

3 对圆周摆测重力加速度不确定度的分析

3.1 直接测量的不确定度［5］

不确定度可分为A类、B类进行评定。测量列平均值的标准偏差为

对A类，若测量为6次，测量结果服从t分布，当p=0.95时，tp=2.57，即

对于B类分量，若其误差极限为△，若仪器误差服从均匀分布C=，当 p=0.95 时，kp=1.96，那么

(8)式中的 z可以分别表示 l、d1、d2、H1、H2，那么

直接测量z的合成不确定度为

3.2 间接测量量的不确定度

对间接测量 y=f(z1，z2，…，zi，…zm)，则 y 的标准不确定度 uc(y)为

y的相对不确定度ur(y)为

考虑(5)、(11)式，重加速度的相对不确定度为

由(17)式知，要减小A对ur(g)的影响，应合理选择测量工具，而T对ur(g)的影响为主要因数，应合理调整圆锥摆实验系统显得尤为重要(调整圆锥摆实验系统平衡，合理选择驱动电压、摆长、小球质量等)。

4 测量数据及结果

4.1 对各种长度(l、d1、d2、H2)的测量

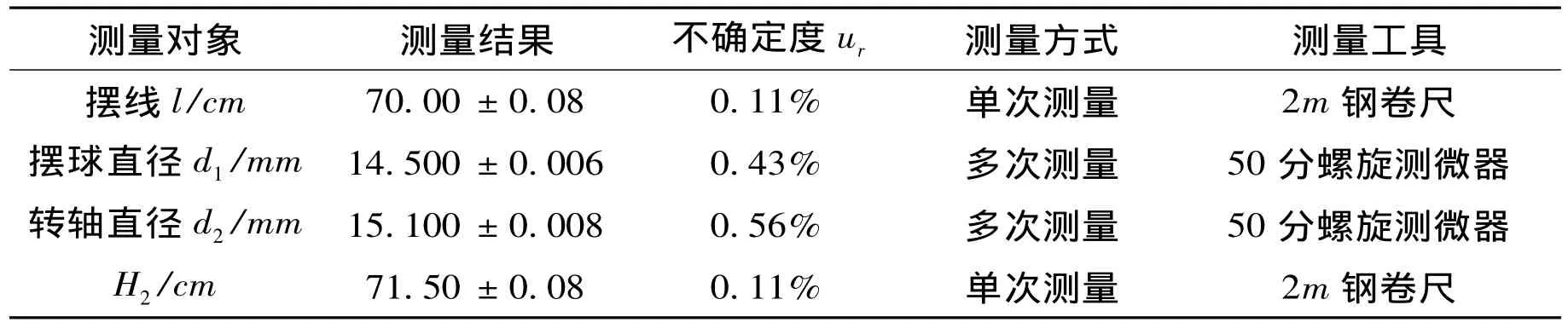
表1 对各长度(l、d1、d2、H2)的测量

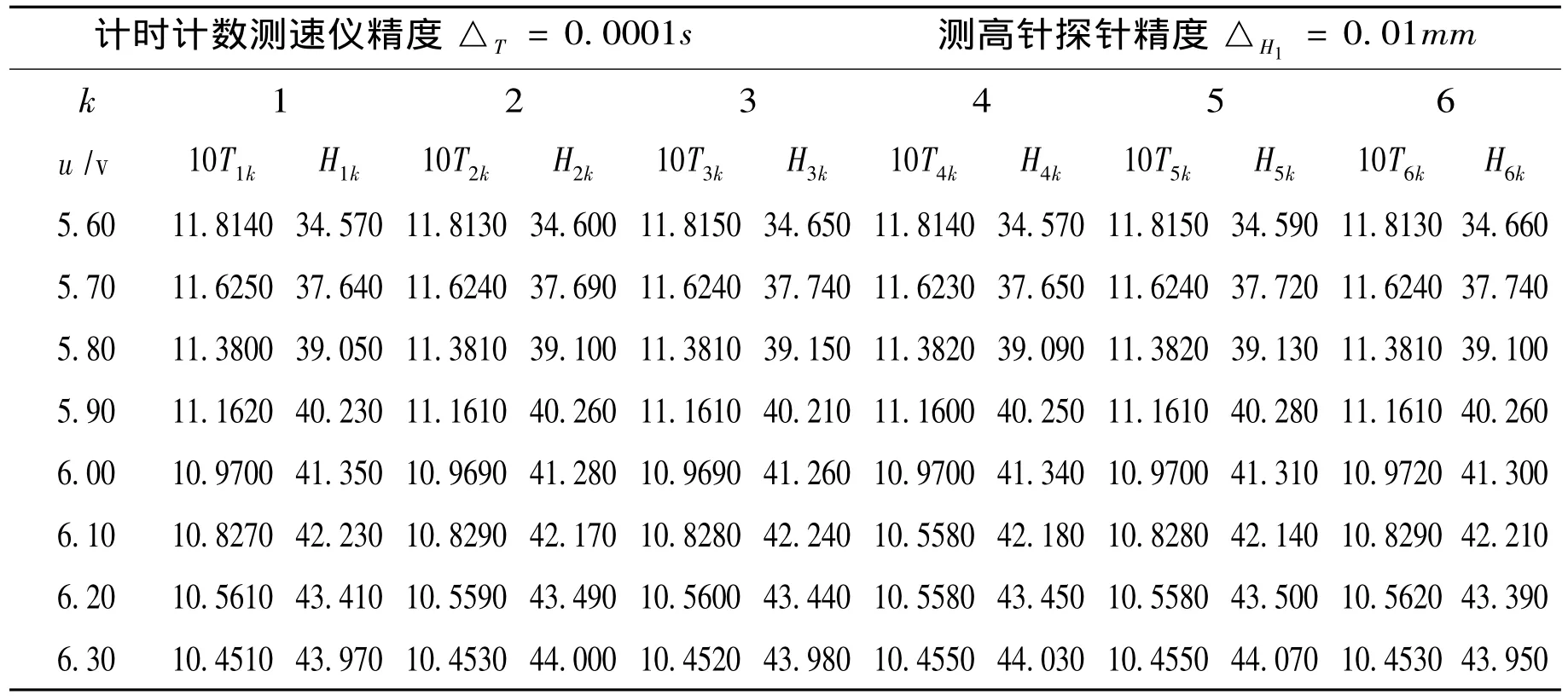
表2 不同电压下对应的周期T和H的测量值

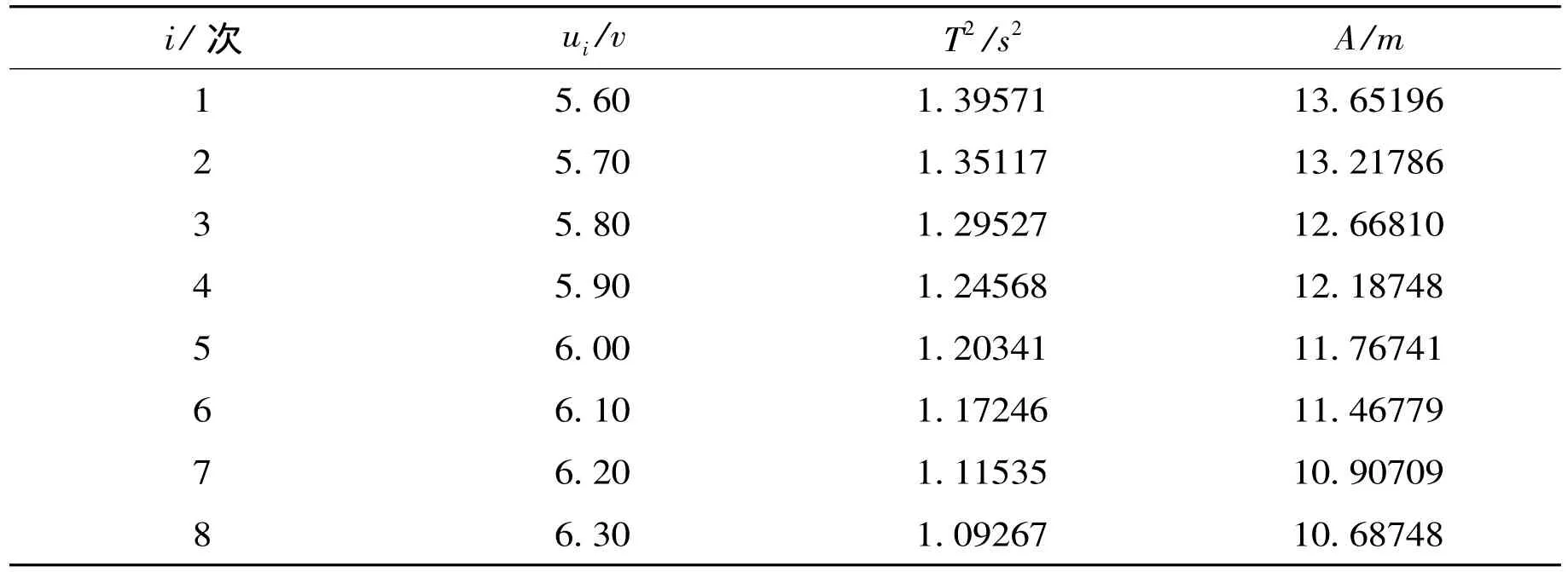
表3 由表1、2不同电压下的T2，A的实验数据

4.2 用Spss分析软件作A－T2定标曲线

把表3实验数据输入Spss软件中，应用Spss软件中的曲线估计功能，以长度综合测量量A为因变量，以做圆锥摆运动的周期平方(T2)为自变量，可得其定标方程为

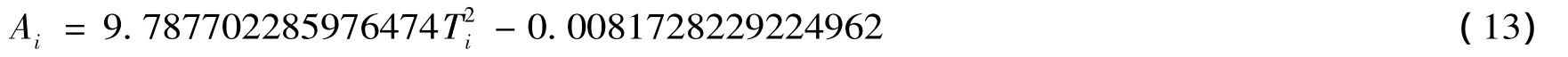
所得曲线如图4所示。

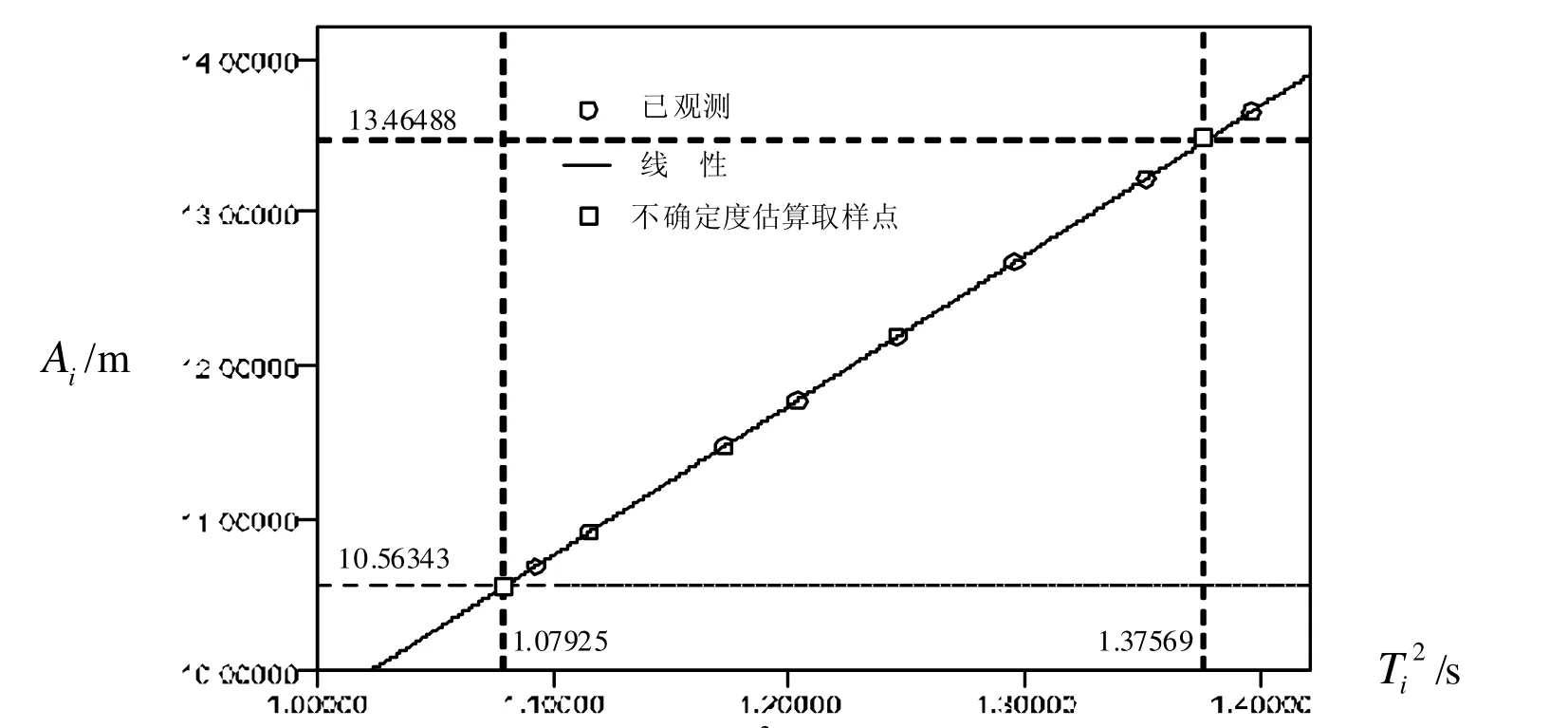
图4 A－T定标曲线

4.3 对重力加速度不确定度的估算

根据图4的A－T2定标曲线，在直线上适当取样值，合理估算g的不确定度。由(13)可得

由(15)可得

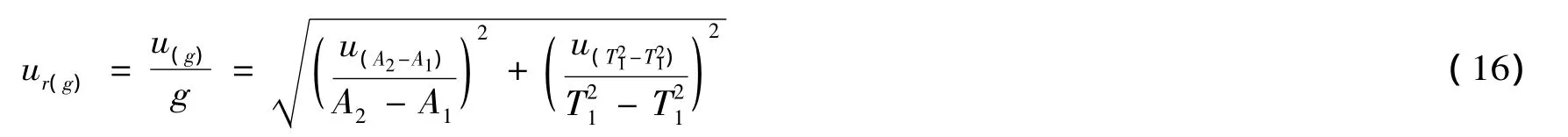
由图4不确定度评定取样点，结合(14)、(15)、(16)可得表3实验结果。

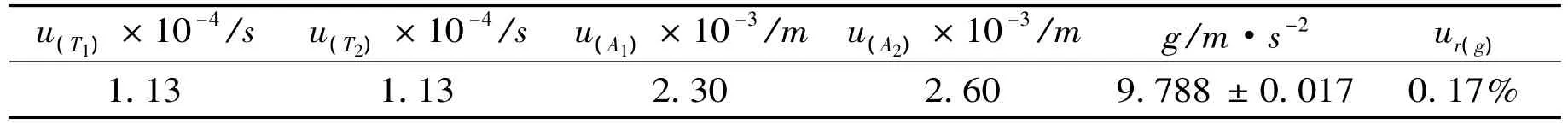
表3 实验结果

由纬度，海拔修正的重力加速度理论公式［6］为

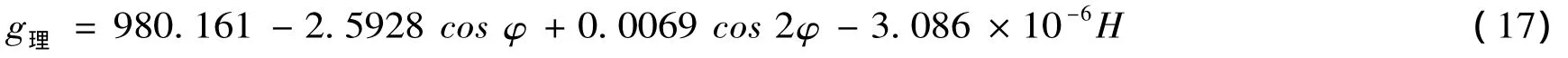
(17)式中，φ表示纬度，H表示海拔。经查阅，云南楚雄地处于北纬25.03°，海拔1773m，因此重力加速度理值为g理=9.783m/s2。

5 结论

由表3数据，应用Spss软件分析得定标方程(13)式及其图4，并得到Ai—T21定标曲线图。得出了自制圆锥摆的长度综合量(Ai)与圆锥摆周期的平方(T2i)成线性关系，实验曲线与理论分析(5)式具有一致性;

由表2、3驱动电压数据可知，若摆长设为70cm，小球质量为20g时，经多次实验验证，圆锥摆的驱动电压应控制在6—7伏，这样可以有效保证小球所做圆锥摆动运动较为平稳。若驱动电机电压低于6伏，小球所做圆锥摆运动会有起伏现象，使得对周期测量偏差较大，若驱动电机电压高于7伏，小球所做圆锥摆运动必须考虑空气阻尼的影响，存在滞后现象，使得测量原理原理的分析不够准确。

能够得到较为理想的(13)式、图4、表3的实验结果，除了借助了强有力的计算机辅助(Spss软件)分析手段外，表明所测量数据(表1、2)的质量较高，说明圆锥摆系统的调平工作，驱动电压值，计时系统的选择较为合理，摆球每次起始状态控制较好，使得因仪器或人为因素所致的偶然误差与系统误差已降为较小。

由表3重力加速度的实验结果，对照由纬度、海拔所修正重力加速度(17)式的计算结果，二者吻合度较好，尤其查看表3中的ur(g)，由该实验方案所得重力加速度的实验值只在千分位上可疑，而以往的实验方案所得重力加速度的实验值一般为十分位或百分位可疑。表明自制圆锥摆实验系统测量周期是合理的，借助Spss软件分析实验数据可提高实验结果的分析精度。

［1］安学立，田存伟.用单摆法测重力加速度实验中单摆周期的测定 ［J］.物理通报，2012，(03):74—75.

［2］朱道云，庞玮等.多管落求法测量重力加速度 ［J］.实验科学与技术，2012，29(04):59—61.

［3］郭敏强，郭启凯等.基于单片机的单摆法智能重力加速度测量装置的研制 ［J］.科学技术与工程，2012，12(26):6766—6771.

［4］宋志刚.SPSS 16.0 guide to data analysis［M］.北京:人民邮电出版社，2008:115—186

［5］丁相云，王新春等.用气轨系统与Spss标定物体的惯性质量 ［J］.大学物理实验.2012，25(03).

［6］张立.大学物理实验 ［M］.上海:上海交大出版社.1998:23—30.