干扰床分选机数学模型初探①

李 梅

(煤炭科学研究总院唐山研究院，河北唐山 063012)

0 引言

近年来，干扰床分选机已经成功地应用于粗煤泥的分选领域，由于其具有生产效率高、运行和维护成本低、自动化程度高等优点，干扰床分选机的应用还在逐步增加。干扰床分选机的结构见图1，物料从分选机主体的顶部通过给料装置进入槽体，与从槽体底部给入的上升水流相遇，形成干扰床层，固体颗粒在槽体内做干扰沉降，沉降速度低的颗粒随上升水流进入溢流而沉降速度大的颗粒进入底流，也就是低密度细颗粒的物料进入溢流而高密度粗颗粒的物料进入底流。

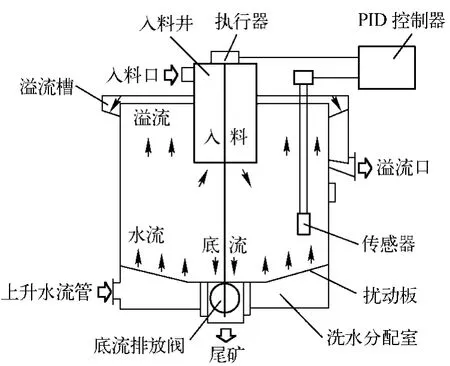
图1 干扰床分选机原理图

干扰床分选机的分选机理复杂且影响因素较多，因此有时操作人员要寻找最佳的操作条件是一件很困难的事，因此，有必要构建一个包括所有干扰床分选机设计和操作参数的数学模型，以预测给定条件下的分选结果或者各参数对分选过程的影响。模型将有助于寻找最佳的设计参数和运行条件。

国外目前已有一些描述颗粒的分选、预测干扰床分选机分选结果的数学模型。这些数学模型可以分成三类:简单的经验公式模型、数质量平衡模型和计算流体力学模型。分别由Galvin和 Das开发的模型属于第一类，Kohmuench模型是典型的数质量平衡模型，XIA利用计算流体力学的欧拉－拉格朗日法模拟了干扰床中的流体流态、颗粒运动和分选机理。在前两类模型中均利用干扰沉降速度经验公式确定颗粒在运动中的速度，而确定颗粒的自由沉降速度是确定干扰沉降速度的第一步，因此，作为构建数学模型的初步探索，本文主要探讨颗粒自由沉降速度的计算。

1 数学模型中自由沉降末速的计算

Galvin模型中颗粒自由沉降末速由式(1)计算得出，

式中Ut是颗粒自由沉降末速，Re是雷诺数，μ是流体粘度，ρ是流体密度，d是颗粒的直径。雷诺数利用Zigrang和Sylvester提出的公式(2)计算

式中ρs是颗粒的密度，g是重力加速度

Das模型中也使用公式(1)计算颗粒自由沉降速度，但是使用了不同的公式计算其中的雷诺数。Das模型利用公式(3)计算雷诺数的数值。

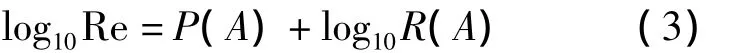
式中 P(A)=［(0.0017795A－0.0573)A+ 1.0315］A－1.26222

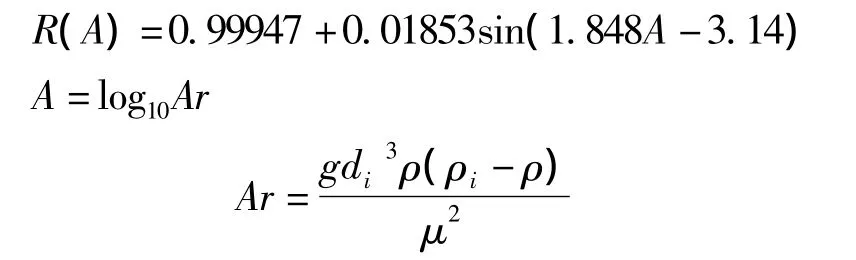
另外，有文献指出阿连公式是确定干扰床分选机中颗粒自由沉降速度的最佳公式【5】，阿连公式见公式(4)

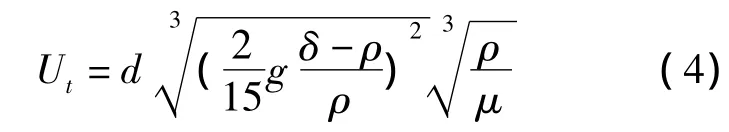
2 颗粒自由沉降速度实验

为了验证上面提及的公式计算结果的准确性，笔者进行了颗粒的自由沉降实验。研究中使用高度800 mm、直径200 mm的自由沉降柱作为实验设备。

本研究所用煤样来自山西省某选煤厂。煤样被分为五个密度级别，每个密度级别又被分成五个粒度级别，共25个煤样。通过自由沉降速度实验测定各颗粒自由沉降末速，结果见表1。表中以平均粒度来代表该粒度级的粒度，以平均密度来代表该密度级别的密度。

3 结果与讨论

由模型中经验公式计算得到的颗粒自由沉降末速和实验测得颗粒自由沉降末速分别见表1，Galvin模型中颗粒自由沉降末速随颗粒粒度、密度变化规律见图2，Das模型中颗粒自由沉降末速随颗粒粒度、密度变化规律见图3，阿连公式计算得到的颗粒自由沉降末速随颗粒粒度、密度变化规律见图4，实验测得颗粒自由沉降末速与颗粒粒度、密度关系如图5所示。

图2 Galvin模型自由沉降末速

图3 Das模型自由沉降末速

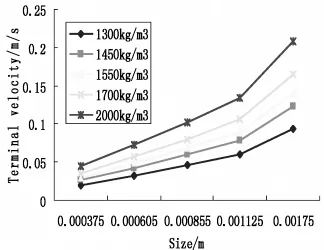
图4 阿连模型自由沉降末速

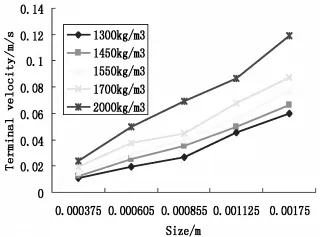
图5 自由沉降末速试验结果

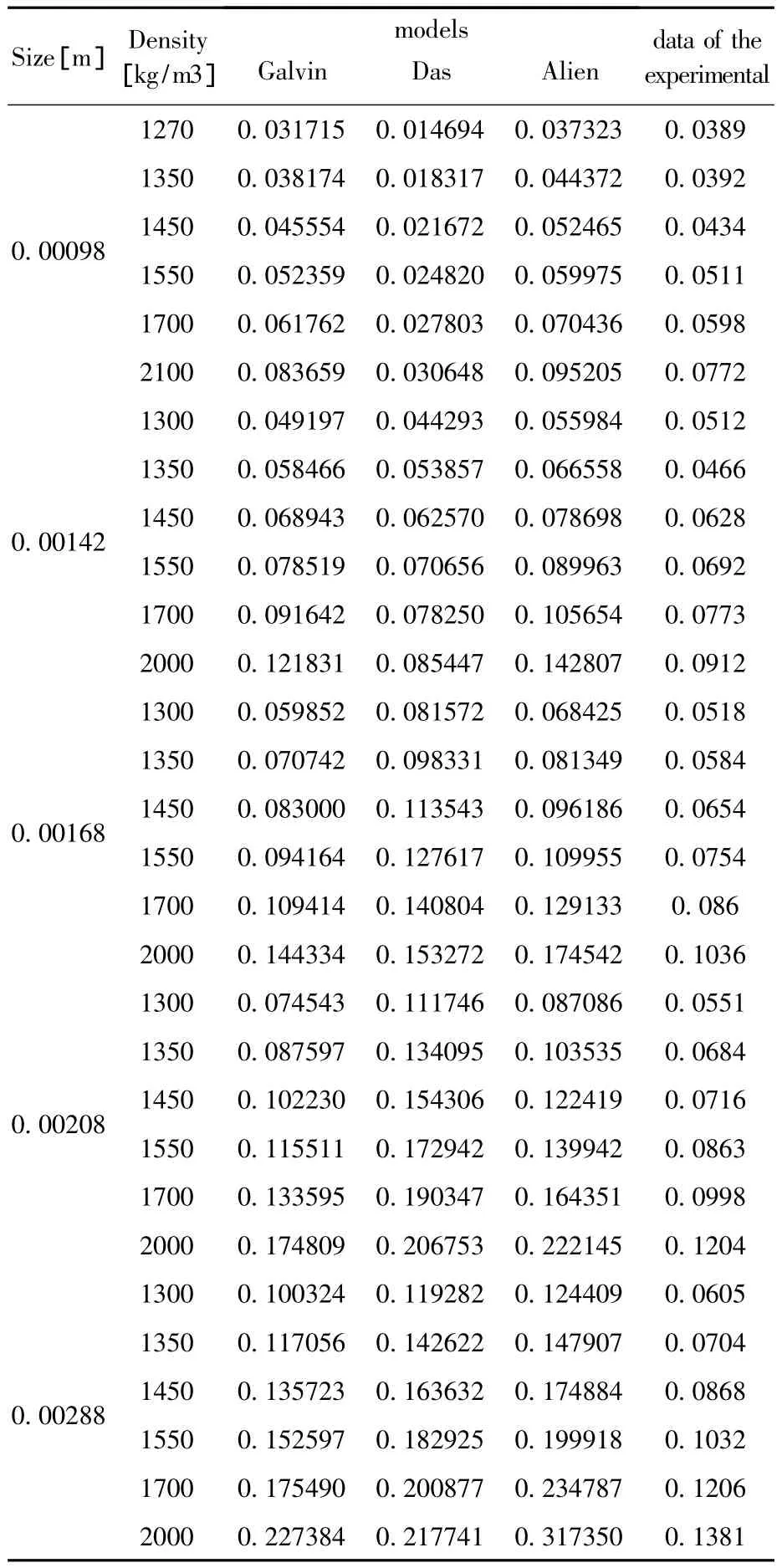
表1 自由沉降末速模型计算结果及试验结果

从表1中可以看出，Galvin模型中，颗粒的自由沉降速度随着粒度和密度的增加呈现增加的趋势，同样的，Das模型计算结果和阿连公式计算结果也呈现相同趋势。图1、2、3更清楚地表现了这一趋势。从图5中可以看出，颗粒自由沉降速度实验所获得的数据表明，颗粒自由沉降速度随着颗粒粒度和密度的增加而升高。因此，模型计算结果与实验数据在趋势上吻合度很好。为了更精确地评估各模型的适用性，本文计算了各模型模拟结果与颗粒自由沉降速度实验结果的偏差值，结果见表2。

表2 各模拟计算结果与试验结果偏差值

由表2可以看出，Galvin模型的计算结果与实验结果的平均偏差值最低，因此可以认为该模型中计算自由沉降速度的关系式更适于用来计算干扰床分选机中颗粒自由沉降速度值。

4 结论

为了建立干扰床分选机数学模型，本文首先讨论了颗粒自由沉降速度的计算方法，将模型计算结果与实验室颗粒自由沉降速度实验结果进行对比。利用Galvin模型和 Das模型以及阿连公式计算颗粒自由沉降速度，通过颗粒自由沉降速度实验测定了30个窄粒度级、密度级样品。通过对比发现Galvin模型计算结果与实验数据最为接近，因此，在今后干扰床分选机数学模型的进一步研究中建议使用Galvin模型计算颗粒自由沉降速度。

［1］ Galvin，K.P..Dense medium separation using a teetered bed separator［J］.Mineral Engineering，1999，12(9):23

［2］ Das，A.and B.Sarkar.Prediction of separation performance of Floatex Density Separator for processing of fine coal particles［J］.International Journal of Mineral Processing，2009，91:9

［3］ Kohmuench，J.N..Improving efficiencies in water－based separators using mathematical analysis tools［J］.Virginia Polytechnic Institute.2000，199

［4］ Xia，Y.K..CFD simulation of fine particle gravity separation in hindered－settling bed separators［J］.Chemical Product and Process Modeling，2007，2(3):11

［5］ 刘文礼.干扰床分选机分选粗煤泥的规律研究［J］.选煤技术，2007，(4):11－13