基于小波变换和GM-ARMA的导弹备件消耗预测

赵建忠 徐廷学

(海军航空工程学院兵器科学与技术系，烟台 264001)

葛先军 尹延涛

(海军航空工程学院科研部，烟台 264001)

备件是进行导弹装备使用和实施维修等保障任务的重要物质基础，准确地预测备件的消耗才能在有限的经费情况下，最大限度地满足导弹装备保障的备件需求.在备件预测领域，时间序列分析由于避免了影响因素调查与筛选、多重共线性等难点而得到广泛应用.导弹备件消耗大都呈现“短周期、小样本”的特点，这表明依靠大样本数据进行建模的方法来预测导弹备件的消耗，很难达到预期效果.灰色模型(GM，Grey Model)是建立系统运行趋势模型的有效方法，适用于动态预测，且只需知道少量已知信息就可建立预测模型.另外，自回归移动平均模型 (ARMA，Autoregressive and Moving Average)，是分析平稳随机信号的一种成熟而有效的方法，能处理周期性变化的序列，且建模时所需数据量少.由于2种模型对于时间序列的预测各有侧重，一些学者提出了GMARMA组合模型(grey model and autoregressive integrated moving average model)［1］.但子模型 GM(1，1)模型对波动大、非线性、非平稳的序列难以取得满意的预测效果，而数据变换技术为建立灰色模型创造先决条件;ARMA模型参数的估计过程是复杂的非线性回归过程，导致ARMA模型参数估计成为模型运用的一个难点，而阻尼最小二乘法为其提供了一条有效的途径.为此本文提出了改进的GM-ARMA模型以克服上述缺点，称为RGM-ARMA模型(revised GM-ARMA).

导弹备件消耗大都呈现非线性、非平稳特征，导致利用RGM-ARMA模型进行导弹备件消耗预测误差仍偏大.小波变换是近年来兴起的一种新的信号分析处理技术，具有多分辨分析的特点，在时域、频域都具有表征信号局部特征的能力，是处理非平稳随机时间序列的一种有效方法［2］.目前，小波变换技术广泛应用于信号处理、图像处理、计算机视觉等领域，但被用于备件预测方面的研究还几乎没有.为了解决备件消耗预测问题，本文尝试将小波变换技术引入到备件消耗预测领域.

至此，在分析导弹备件消耗特性以及备件消耗预测模型研究现状的基础上，提出一种基于小波变换和RGM-ARMA的导弹备件消耗组合预测方法，称为 WGM-ARMA模型(wavelet transform，revised grey model and autoregressive integrated moving average model).在充分拟合低频信息的同时，又避免对高频信息的过拟合，从而提高了非平稳时间序列的预测精度，为备件消耗预测提供了一种新的思路.

1 小波变换理论

小波变换有很多算法，常用的有快速变换算法:Mallat算法和A Trous算法等.本文根据备件消耗序列长度，采用Mallat算法，即塔式算法.该算法从空间概念方面形象地说明了多分辨分析特性，并给出了信号分解不同频率通道的算法及重构算法［3］.

2 GM-ARMA模型的改进

2.1 基于背景值优化和数据变换技术的改进GM(1，1)

2.1.1 振荡序列的改进

文献［4－5］论证了平移变换可以使任意的原始数据序列X变为一个单调递增的序列X1;文献［6－7］几何平均变换不但可使序列X1的随机波动性减弱，消除冲击干扰项对系统造成的数据“失真”现象，而且还能保持原有数据序列X1的单调性，并提高序列X1的光滑性.因此，通过对平移变换和几何平均变换后生成得到的数据序列建立GM(1，1)模型，可以有效地提高预测模型的模拟精度.

2.1.2 背景值的优化

设 X={x(1)，x(2)，…，x(n)}为原始时间序列，计算背景值 Z(1)时，Z(1)(i)=θx(1)(i－1)+(1 － θ)x(1)(i)(i=1，2，…，n).其中，X(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}为原始数据序列的一次累加序列，θ为(0，1)之间的待定常数.

2.1.3 模型的建立

先对X进行平移变换，得到的序列记作

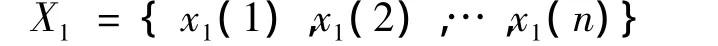
其中，x1(k)=x(k)d1，k=1，2，…，n;然后对 X1进行几何平均变换，生成的序列记作

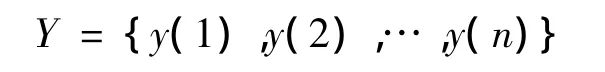
其中，y(k)=x1(k)d2，再以 Y={y(1)，y(2)，…，y(n)}为原始序列建立GM(1，1)微分方程.求解并作一次累减生成得

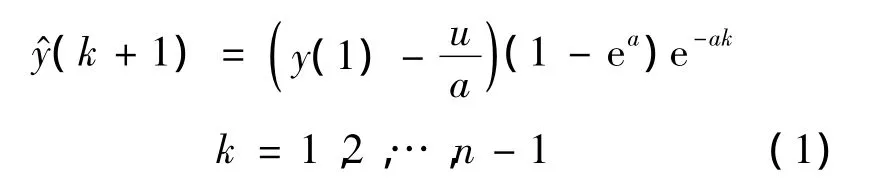
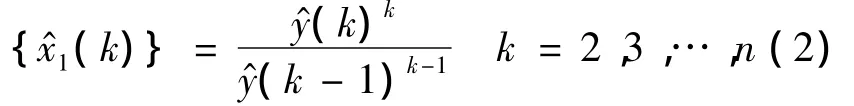
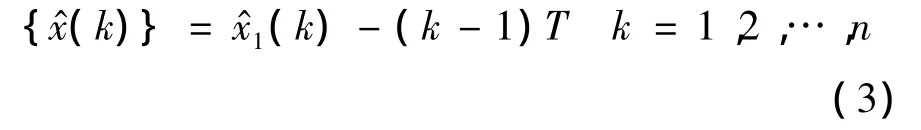
2.2 基于阻尼最小二乘法优化的ARMA

本文利用反向过程确定数据初值，结合阻尼最小二乘法，求解ARMA模型的参数［8－9］.

条件最小二乘法中的条件是指初值条件［10］，当一时间序列用ARMA模型来拟合，假设此序列中第一个时刻之前的p个时刻的值为0或者均值，相对应的残差序列的前q个时刻的值为0.

首先用反向过程确定初值，假设时间序列x1，x2，…，xn，需要去估计 x－i(i=1，2，…，n)，可以由反向模型所产生算子:φ(F)xk=θ(F)φk.

由于该算子的平稳性，在一定的范围k=ε以外，估计值基本上等于0［11］.因此，对充分的近似值，用式(4)来求解.

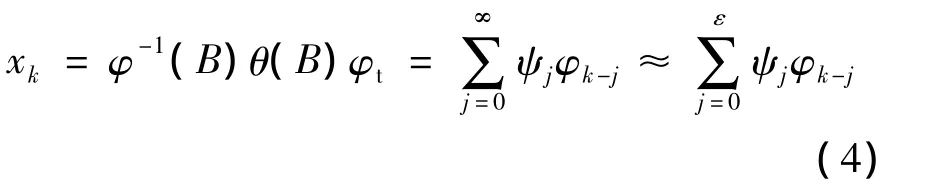
将混合过程用一个ε阶滑动平均过程代替.接着将模型线性化，而且要极小化

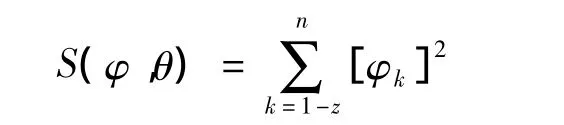
将［φk］用 Taylor级数展开，m=p+q个参数用β作为(φ，θ)的记号，在该值附近有一组推测的对应参数值 β0=(β1，0，β2，0，…，βm，0)，则有

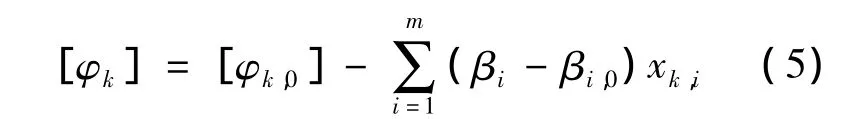
再使用阻尼最小二乘法进行计算，阻尼最小二乘法是Newton法与最速下降法的结合，不仅收敛速度快，而且精度高［12－13］.

对于给定的模型，值［φm|x，β1，0，β2，0，…，βm，0］对于 k=1 － ε，…，n 用递推方法，然后对［φm|x，β1，0+ δ1，β2，0，…，βm，0］重复递推计算，继而又对［φm|x，β1，0，β2，0+ δ2，…，βm，0］进行递推 计算，由

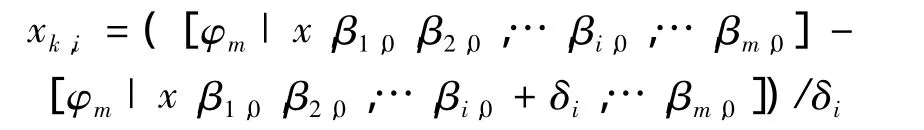
可得到具有足够精度的所需导数负值，求取［φk］，最后计算出预期的ARMA模型参数.

3 WGM-ARMA模型的构建

在上述分析和研究的基础上，对导弹备件消耗预测的思路和框架进行规划.首先对备件消耗序列进行分解与重构，然后对低频和高频信息分别建模和预测，最后将各个预测结果进行叠加，便得到原始序列的预测结果.预测框架见图1.

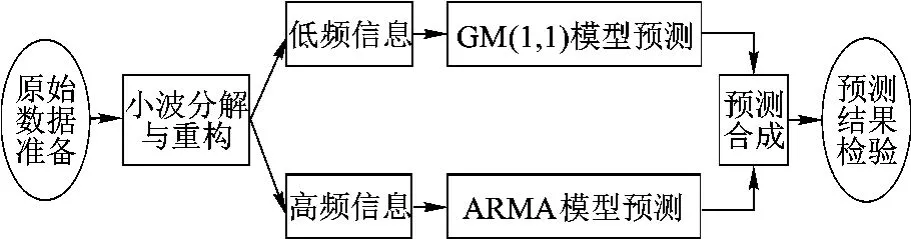
图1 基于WGM-ARMA的导弹备件消耗预测框架图

在WGM-ARMA模型中，需要整合3种模型，这里模型的整合优化是建立WGM-ARMA模型的关键.首先要对小波基和分解层数进行参数化:参数m代表小波基，参数k代表分解层数.在灰色模型GM(1，1)中的特征参数是θ，在ARMA模型特征参数是(p，q)，在小波分解的特征参数是(m，k)，而整合GM(1，1)，ARMA模型和小波分解的过程就是找到特征参数组合(θ，p，q，m，k)最佳组合的过程.建立组合模型基本的前提条件是θ，(p，q)和(m，k)的选择必须基于相同的统计准则［14］.显然参数(m，k)可以用总绝对值误差(TAE，Total Absolute Error)准则［15］选择，因此模型的整合可以依据TAE准则进行选择.

对于给定的时间序列 X=(x1，x2，…，xn)，已知小波基方程m和小波分解的层数k，根据小波分解，该时间序列X可以被分解为

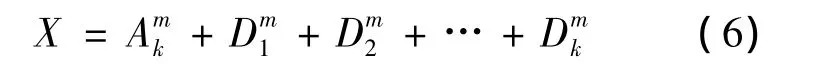
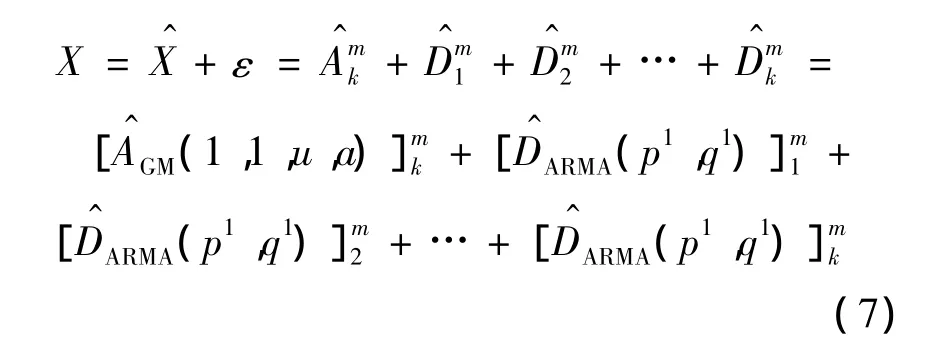
对参数(m，k，θ，p1，q1，p2，q2，…，pk，qk)设定上下限，得到一个离散的参数空间:

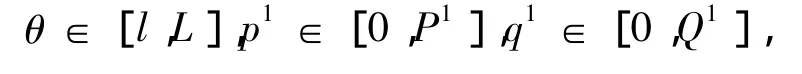
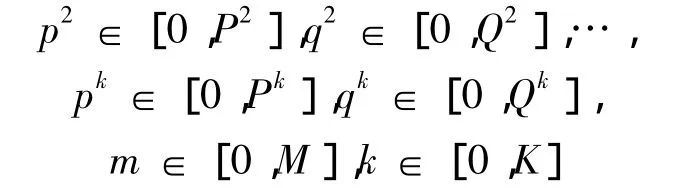
这样对于参数组合(m，k，θ，p1，q1，p2，q2，…，pk，qk)，通过式(7)计算出拟合序列 X=(x^1，x^2，…，x^n)，并计算出对应的总绝对值误差为

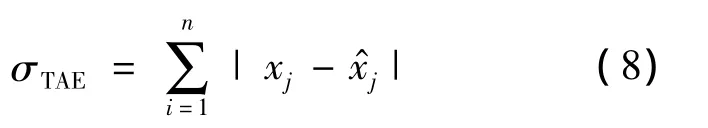
而最终的WGM-ARMA模型满足:

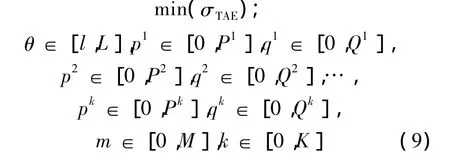
4 实例分析

据调研分析，某型导弹装备的使用和维修保障过程中，由于电流电压不稳或电子器件到寿、振动或冲击、橡胶老化或受力等因素，导致导弹装备出现电子件短路断路或击穿烧蚀、机械件断裂或磨损、橡胶件断裂或磨损等现象，进而导致相应备件的消耗.这里统计了该型导弹装备某种备件1998年－2010年的消耗情况(见表1).

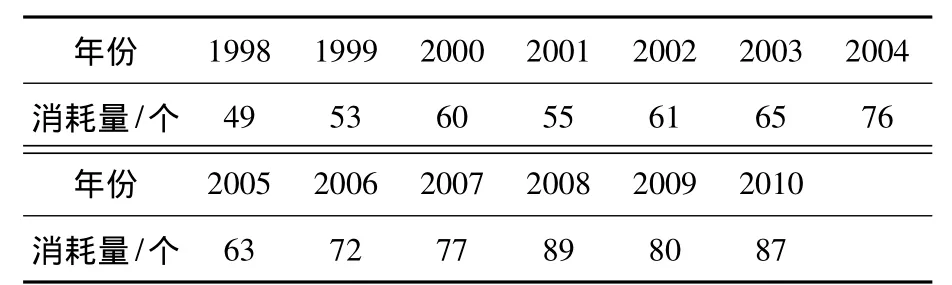
表1 1998年－2010年某种导弹备件的消耗数据

4.1 数据分析

由表1知，备件消耗序列是非平稳的时间序列，先采用小波分析理论把备件消耗序列进行分解和重构.这里数据样本共13组，选取前10组数据样本构建模型，拟合模型;后3组数据样本用来作为预测值的比较对象，以检验预测效果的好坏.

4.2 消耗预测

4.2.1 参数确定

首先对参数(m，k，θ，p1，q1，p2，q2，…，pk，qk)设定上下限.对参数m进行编号，如表2所示.经研究比较，对参数(k，θ，p1，q1，p2，q2，…，pk，qk)定义的上下界为 k∈［1，2，…，6］，θ∈［0，0.1，…，1］，p1，q1，p2，q2，…，pk，qk∈［0，1，…，5］.到此，对于每个参数组合(m，k，θ，p1，q1，p2，q2，…，pk，qk)都可以基于10个历史数据X=(x1，x2，…，x10)通过式(7)建立模型，并得到拟合序列X^，并通过式(8)计算出相应的σTAE，且WGM-ARMA模型满足式(9).

上述式(7)～式(9)的计算过程可以用Matlab编程实现，最终计算出来的σTAE最小的参数组合为:m=4，k=2，θ=0.6，p1=2，q1=1，p2=2，q2=2.根据第3节参数定义和表2可知，m=4表明首先要用小波基方程“db3”，k=2表明通过小波分解把原始序列X分解2层，低频逼近信号、高频细节信号和重构信号见图2.

表2 小波基方程的编号

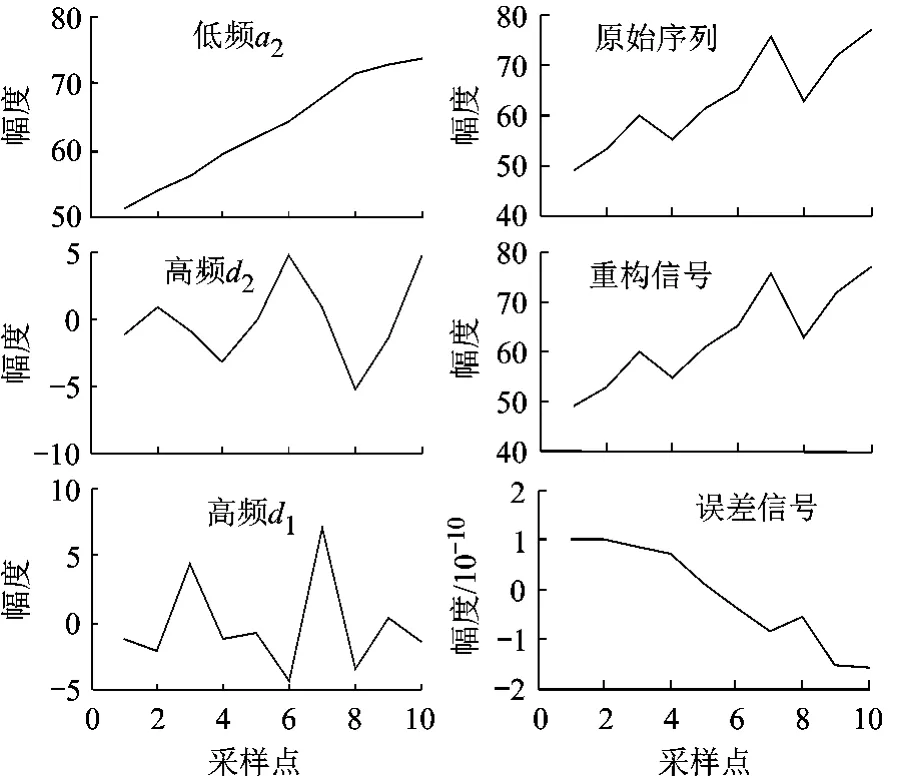
图2 备件消耗时间序列及用db3小波分解后重构结果

由于db N小波具有正交、时频支撑、高正规性和Mallat快速算法等特点，对非平稳时间序列的分解具有很好的特性，但消失矩不能太高，一般不超过4，即db2～db4比较合适;分解过程中本身存在计算误差，层数越多，误差越大，计算上的误差会带来预测的误差，使预测精度下降，一般为2～5层［16］.由此可见，在分解过程中小波基和分解层数的选择是比较合理的.

4.2.2 低频逼近信号预测

对小波分解后的低频逼近信号采用改进GM(1，1)模型(θ=0.6)进行预测，数据拟合情况如图3所示.后验差比值 C=0.032＜0.35，小误差概率P=1＞0.95，预测模型等级为优，可以用于低频逼近信号预测.

4.2.3 高频细节信号预测

对小波分解后的高频信号采用ARMA模型(p1=2，q1=1，p2=2，q2=2)进行预测，数据拟合情况及其误差相关系数如图4和图5所示.由此可见，ARMA模型的预测信号值和原始信号很接近，预测精度较高，可以用于高频细节信号的预测.

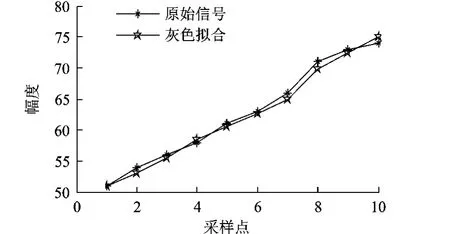
图3 低频信号的灰色拟合效果

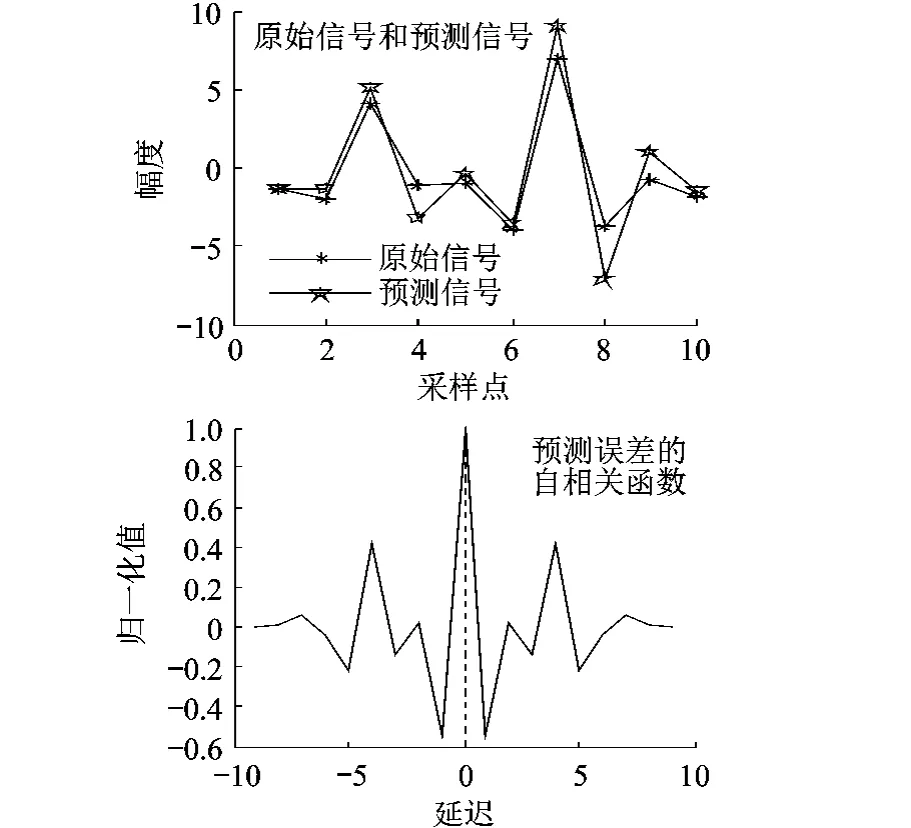
图4 高频信号1的ARMA拟合及其误差相关系数

图5 高频信号2的ARMA拟合及其误差相关系数

4.3 结果分析

在上述分析的基础上，把低频逼近信号和各层高频细节信号在第11～13时间点的预测值相加，便得到2008年－2010年的备件消耗量.作为对比，再采用传统的 GM(1，1)、改进的 GM(1，1)、ARMA模型、RGM-ARMA模型，分别对备件消耗进行预测，这5种方法的预测结果如图6所示，平均相对误差(MRE，Mean Relative Error)分别是0.0622，0.0465，0.0497，0.0344，0.0152.

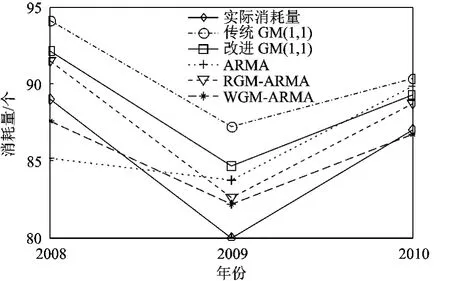
图6 预测误差对比

5 结 束 语

本文尝试把小波变换引入到导弹备件消耗预测中，提出了基于小波变换和改进GM-ARMA的导弹备件消耗预测方法，其显著特点是运用小波变换技术将非平稳的备件消耗时间序列分解为多层频率成分更加单纯、相关性更强的序列，并且针对各层的特点，用改进的GM(1，1)和ARMA模型分别对分解后的非线性低频趋势信息和相对平稳高频信息进行预测，叠加各子序列的最终预测效果优于单一预测模型.更为重要的是，本文提出了一个基于小波变换的全新的构建组合预测模型的思路，进而构建出更多更精确的备件预测模型.研究结果表明，基于小波变换的多种模型相结合的方法，不仅能够反映原始备件消耗数据的结构特征及变化规律，而且还可以发挥各模型的优势，取得了较高的预测精度且预测性能稳定，对进一步解决实际问题具有良好的应用前景.

References)

［1］胡效雷，何祖威.基于GM-ARMA组合模型的年电力需求预测［J］.广东电力，2007，20(2):10 －13 Hu Xiaolei，He Zuwei.Forecasting about annual electric consumption based on GM-ARMA combined model［J］.Guangdong Electric Power，2007，20(2):10 －13(in Chinese)

［2］ Amjady N，Keynia F.Short-term load forecasting of power systems by combination of wavelet transform and neuro-evolutionary algorithm［J］.Energy，2009(34):46 －57

［3］马林才，许玮珑，刘大学.基于小波变换的城市市区典型路段交通流量预测［J］.控制与决策，2011，26(5):789 －793 Ma Lincai，Xu Weilong，Liu Daxue.Prediction model of traffic flow along typical roads in city urban district based on wavelet transform［J］.Control and Decision，2011，26(5):789 －793(in Chinese)

［4］钱吴永，党耀国.基于振荡序列的GM(1，1)模型［J］.系统工程理论与实践，2009，29(3):149 －154 Qian Wuyong，Dang Yaoguo.GM(1，1)model of oscillation sequences［J］.Systems Engineering Theory ＆ Practice，2009，29(3):149－154(in Chinese)

［5］ Bo L，Yong W.Optimized GM(1，1)grey model based on connotation expression［J］.Journal of Grey System，2007(3):133－136

［6］赵宇哲，武春友.灰色振荡序列GM(1，1)模型及在城市用水中的应用［J］.运筹与管理，2010，19(5):155 －166 Zhao Yuzhe，Wu Chunyou.GM(1，1)model of grey oscillation sequences and its application to urban water consumption forecasting［J］.Oerations Research and Management Science，2010，19(5):155－166(in Chinese)

［7］ Wang M H.Grey-extension method for incipient fault forecasting of oil-immersed power transformer［J］.Electric Power Component and Systems，2004，32(10):959 －975

［8］ Ives A，Abbott K C，Ziebarth N L.Analysis of ecological time series with ARMA(p，q)model［J］.Ecology，2010，91(3):858－871

［9］ Carden E P，Brownjohn JMW.ARMA modeled time-series classification for structural health monitoring of civil infrastructure［J］.Mechanical Systems and Signal Processing，2008，22(2):295－314

［10］ Topres JL，Garcl A，Deblas M，et al.Forecast of hourly average wind speed with ARMA models in Navarre［J］.Solar Energy，2005(79):65－77

［11］ Kim H J，Shin K S.A hybrid approach based on neural networks and genetic algorithms for detecting temporal patterns in stock markets［J］.Applied Soft Computing，2007，7(2):569 －576

［12］ Bermudez JD，Segura JV.A decision support system methodology for forecasting of time series based on soft computing［J］.Computational Statistics ＆ Data Analysis，2006，51(1):177－191

［13］ 何永沛.ARMA模型参数估计算法改进及在股票预测中的应用［J］.重庆工学院学报:自然科学版，2009，23(2):109 －112 He Yongpei.Improved algorithm of parameter estimating for ARMA model and its application in the stock markets forecasting［J］.Journal of Chongqing Institute of Technology:Natural Science，2009，23(2):109 －112(in Chinese)

［14］吴朝阳.改进的灰色模型与ARMA模型的股指预测［J］.智能系统学报，2010，5(3):277 －281 Wu Zhaoyang.Forecasting stock index based on revised grey model and ARMA model［J］.CAAI Transactions on Intelligent Systems，2010，5(3):277 －281(in Chinese)

［15］吴朝阳.小波变换和GM-ARMA组合模型的股指预测［J］.智能系统学报，2011，6(3):279 －282 Wu Zhaoyang.Using wavelet transformation and a GM-ARMA model to forecast stock index［J］.CAAI Transactions on Intelligent Systems，2011，6(3):279 － 282(in Chinese)

［16］李持佳，焦文玲，赵林波.燃气短期负荷预测的小波分析综合模型［J］.天然气工业，2007，27(8):103 Li Chijia，Jiao Wenling，Zhao Linbo.A synthesis wavelet analysis method for short-term gas load prediction［J］.Natural Gas Industry，2007，27(8):103(in Chinese)