不确定型AHP 中专家可信度计算方法研究
陈孝珍,张学军
(1.南阳理工学院 土木工程学院,河南 南阳473004;2.南阳理工学院 机械与汽车工程学院,河南 南阳473004)
0 引言
利用层次分析法对桥梁结构的耐久性进行评估,建立相应的评估模型,对桥梁结构的性能进行层次化评估,使评估条理更加清晰[1]. 然而由于桥梁耐久性评估过程的模糊性、随机性和复杂性,不同的专家对同一结构的评估具有不确定性和模糊性,因此准确地建立判断矩阵十分困难,同时在评估过程中各层次的权重系数的选择是能否对桥梁结构的性能做出准确判断的关键[2],现有层次分析法中的权重系数的选择主要依赖专家的经验,因而建立的矩阵有较大的主观性[3-4].
刘文龙等[5]利用不同专家评价的不确定矩阵计算出了相应的权重系数,然后根据每位专家的经验、水平赋予不同的可信度系数,利用加权平均值方法计算最终权重系数.在现有研究中,计算各专家的可信度时首先要把各个专家利用区间数建立的不确定性矩阵转化为确定性矩阵[5]. 由研究可知[6],转换后的确定性矩阵的部分值并不在专家建立的不确定性矩阵的相应区间内,因此在由不确定性矩阵转化为确定性矩阵的过程中就已产生了一定误差,同时各专家对不同指标相对重要性的判断区间的上下限的准确程度也不同,而采用此方法计算得到的专家可信度系数的准确程度则有待于进一步研究.
笔者拟研究桥梁耐久性评估中专家可信度及评估指标权重系数的计算方法,利用现有专家对某桥梁结构指标进行评价构成不确定矩阵,针对于不同专家的评价矩阵分别形成上限矩阵和下限矩阵,利用相似性理论计算各专家评价的上限矩阵和下限矩阵的可信度矩阵,以上、下限矩阵的可信度矩阵的平均值作为不同专家对不同指标的可信度系数.计算权重系数时,在各专家评价的不确定矩阵各区间内随机选取数值作为两个指标间的相对重要性参数,形成多个判断矩阵,分别由各判断矩阵计算权重系数,不同专家判断的指标权重系数取其平均值,然后用加权和求解专家评价的最终权系数.用区间数表示的不确定型判断矩阵可以在很大程度上反映出专家判断的模糊性和不确定性,更好地反映桥梁的实际工作状态、减小不同专家权重系数选择的主观性,使评估结论更具可信性[7].
1 专家可信度计算
1.1 区间数判断矩阵
运用层次分析法对桥梁结构进行耐久性分析时,将评估目标分为目标层、准则层、指标层建立评估模型[6].
将评估模型各层的评估指标两两进行相对重要性比较,构造判断矩阵A,判断矩阵A 可以表达为:A=(aij)n×n,其中aij表示xi与xj关于某个评估指标的相对重要性程度,相对重要性标度如表1 所示[7].

表1 相对重要性标度Tab.1 Relative importance scale
运用层次分析法对结构耐久性进行评估时,某专家对两个指标的相对重要性可用介于1 /9与9 之间的一个数字来表达,但不同专家个人研究经验、偏好以及桥梁结构的本身的模糊性和不确定性,使专家不可能对两因素的相对重要性做出准确的判断,因此用区间数表达两因素间的相对重要性更切合实际[8].
1.2 根据专家建立的指标相对重要性矩阵分别形成上限矩阵和下限矩阵
巴东长江公路大桥是一座双塔双索面漂浮体系预应力混凝土斜拉桥,文献[5]中6 位专家给出了用区间数表达的巴东长江大桥安全性综合评估中的第一级评估指标的两两判断矩阵,如表2 所示.

表2 不同专家的区间数判断矩阵[5]Tab.2 Interval judgment matrix and comprehensive judgment matrix from different experts
由表2 可得,不同专家的判断矩阵的上、下限矩阵,如专家1 判断矩阵的上下限矩阵为

同理,其它专家的判断矩阵的上、下限矩阵可由表2 得到.
1.3 计算专家评价的相似性系数
若有n 维行向量α = (α1,α2,…,αn)、β =(β1,β2,…,βn),α、β 的相似性系数由下式[8]计算得到:

将6 位专家的判断矩阵的上、下限矩阵转化为行向量,利用式(1)计算每位专家的评价的上、下限矩阵与其它专家评价的上、下限矩阵的相似性系数.上、下限矩阵的相似性矩阵分别为η上限=


式中:m 为评判专家数量.
则第i 专家与其他专家评判结果的相似性表示为

将各专家判断矩阵的上、下限矩阵转化为m 个行向量,分别计算6 位专家相应的上、下限相似性系数矩阵:
u上限= (0.166 88,0.166 84,0.166 75,0.166 88,0.165 91,0.166 75)
u下限= (0.166 39,0.166 55,0.166 87,0.166 91,0.166 42,0.166 87).
1.4 专家评价的差异性
将各专家判断矩阵的上、下限矩阵转化为m个行向量α1,α2,…,αm,则各专家对第i 个指标评判值的均值为

则第k 个专家对第i 个指标评判值的差值为

为第k 个专家评判的差异度.
由6 位专家的评判矩阵计算得到上、下限矩阵的差异度为
λ上限= [0.170 78,0.169 87,0.116 71,0.170 78,0.255 16,0.116 71];
λ下限= [0.328 58,0.143 53,0.145 6,0.066 252,0.170 44,0.145 6].
1.5 专家评价的可信度
第k 个专家的可信度ωk为
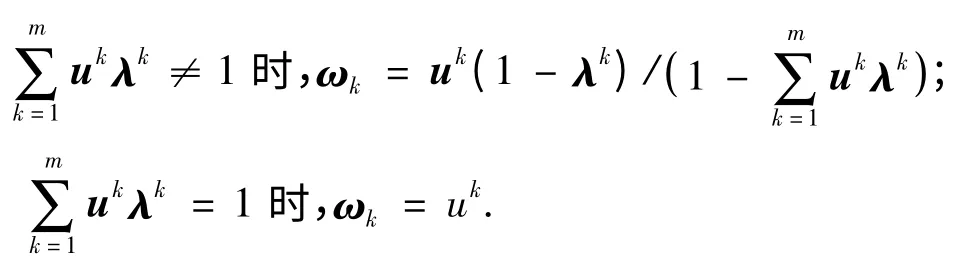
则6 位专家判断矩阵的上、下限矩阵可信度矩阵为
ω上限=[0.166 04,0.166 19,0.176 73,0.166 04,0.148 28,0.176 73];
ω下限=[0.134 10,0.171 19,0.171 03,0.186 95,0.165 70,0.171 03].
6 位专家的可信度取矩阵为判断矩阵的上、下限矩阵可信度的平均值ω 为
ω = [0.150 07,0.168 69,0.173 88,0.176 495,0.156 99,0.173 88].
其中,ωk表示第k 个专家对指标评价的可信度.
2 利用随机理论计算专家对指标评价的系数
根据表2 建立专家的不确定性判断矩阵:

同理其他5 位专家的不确定矩阵也可由表2 得到.
根据各个专家给出的区间数判断矩阵,各专家对两个因素的相对重要程度在相应的不确定矩阵R1,R2,…,R6随机选取,由于随机选取可产生无数个取值,形成多个矩阵. 为便于计算,在各取值区间中每0.5 取一个值形成相应取值的集合.
如由专家1 的不确定性矩阵可形成18 个矩阵确定矩阵,即

运用matlab 计算各判断矩阵的最大特征值λmax,对应式(2)矩阵的最大特征分别为λ1max=3.005 5,λ2max= 3.022 2,λ3max= 3.002 9,λ4max=3.016 5,…,λ15max= 3.013 2,λ16max= 3.036,λ17max= 3.009 2,λ18max= 3.029 1.
由于矩阵都是正反矩阵,因此只要矩阵An×n的最大特征值λmax≥n,则矩阵An×n是一致的[6].对不满足一致性的矩阵予以去除,满足一致性的矩阵作为计算权重系数的判断矩阵.
根据其他5 位专家的不确定矩阵分别可形成18,40,48,24 和40 个确定矩阵,并进行一致性检验,过程与上面相同.
3 权重系数计算
权重系数的计算有和法、根法、特征根法、对数最小二乘法、最小二乘法等,笔者采用和法计算权重系数.利用和法计算权重系数先将判断矩阵的每一列都归一化处理,得到矩阵B = (bij)n×n,然后按B 的行求和就可以得到权重系数,即

以式(2)的满足一致性的矩阵为判断矩阵,计算得到对应的权重系数,专家1 的权重计算结果如下:

则专家1 评价的指标最终权重系数取式(3)中各权重系数的平均值,即

同理可计算其他5 位专家评价的指标权重系数分别为

考虑不同专家的可信度,利用加权和求解6位专家对指标评价的最终权重系数为

刘文龙在计算权重系数时根据专家的经验、水平给每一位专家的评估结果赋予了可信度系数[6],计算得到的权重系数如下:

4 结论
根据不同专家所确定的不确定判断矩阵,本文利用不确定矩阵形成了相应的上限矩阵和下限矩阵,运用相似理论分析了上限矩阵、下限矩阵的相似性、差异性,计算得到了每位专家的可信度.本文计算专家可信度的方法综合考虑了专家对不同指标评判的准确度,同时也考虑了各专家对每一指标评判区间上下限评价的准确程度,充分反映了各专家的研究经历及经验.
在每位专家评价的不确定判断矩阵的基础上,运用随机理论在各评价指标的相应取值区间内随机取值作为两指标间的相对重要性参数,由此形成多个确定判断矩阵计算指标的权重系数,其平均值作为该专家对指标评价的权重系数. 本文中计算指标权重系数的方法减少了现有由不确定判断矩阵向确定性矩阵转化中的误差,使计算得到的权重系数更贴近专家的评价.
利用加权和的方法计算得到的指标的最终权重系数,与文献[4]相比最大误差为1.8%,本文的方法更全面地考虑了专家的水平、专家对不同指标的评价结论,避免了对专家经验、水平评价的主观性.
[1] SAATY T L. The analytic hierarchy process[M]. New York:McGraw Hill,1980.
[2] 闫磊,任伟. FRP 加固桥梁受弯构件的可靠性分析[J]. 郑州大学学报:工学版,2011,32(2):83-86.
[3] LIU B,LI H. Method of factor weights allocation based on combination of fuzzy and rough set[J]. Control and Decision,2007,12(22):1440 -1737.
[4] ZHAO B,REN F,YU H,et al. Research on application of customer satisfaction index model[J]. IEEE Press,2011.
[5] 刘文龙. 基于不确定型层次分析法桥梁安全性评估研究[D].武汉:武汉理工大学土木工程与建筑学院,2005.
[6] 刘均利,方志. 基于灰色关联度的在役双曲拱桥耐久性综合评估[J]. 湖南大学学报:自然科学版,2010,37(9):1 -6.
[7] 谢志坚,刘承平. 模糊数学方法及其应用[M]. 第3 版. 武汉:华中科技大学出版社,2006.
[8] 许树柏. 层次分析法原理[M]. 天津:天津大学出版社,1988.

