基于ADAMS和SIMULINK的气压伺服式六自由度运动平台仿真研究

张玉姝，李军

(哈尔滨工业大学机电学院气动技术中心，黑龙江哈尔滨150001)

六自由度并联机构作为机器人范畴的一个重要方面，得到了越来越深入的研究与广泛的应用。并联机构是相对于串联机构而言的，串联机构的运动是由前一级向后逐级传递的，而并联机构的运动是由几个运动的合成形成的，不会产生累计误差，运动精度高，结构刚度比串联机构高得多，承载能力也得到很大的提高。并且并联机构的运动部件较小，惯性小，速度响应较快，耦合程度与非线性程度也比传统的串联机构运动要小得多，所以整体上说并联机构的动态响应特性比串联机构好。

六自由度运动平台可以完成空间6 个自由度的运动，是并联平台研究的重点，可以模拟空间各种运动姿态，广泛应用到各种训练模拟器、飞船和潜艇空间对接平台、微动机构、并联机床、灵巧机器人以及动感电影、娱乐设备等领域，具有广阔的应用前景。

气动系统具有结构简单、价格低廉、无污染等优点，已广泛应用于社会生产活动的各个领域。随着气动技术的发展，结合气动技术与并联机构特点的气压驱动六自由度运动平台的研究与应用必将达到一个新的高度，并将更好地扩展气动技术与并联机构的应用领域。

1 总体仿真原理

平台位置仿真原理如图1所示。将运动平台的期望位姿反解，得到6 个气缸的位移曲线，作为控制量输入到气动伺服系统模型中，模型实际输出的位移作为反馈值，输入比较器，完成闭环控制。利用三维建模软件搭建平台虚拟模型，作为仿真的样机，虚拟模型的输入为气缸位移，输出为活塞受力，即气动伺服系统的负载。

图1 基于位置反解的平台仿真原理

2 反解算法

设动平台中心点的位置为［x，y，z］，动平台的姿态采用α，β，γ 3 个欧拉角(滚转角、俯仰角、偏航角)表示，对应的旋转顺序为绕x，y，z 轴旋转，则动平台的空间位姿可以用矢量q 来描述，q =［q1，q2，q3，q4，q5，q6］=［x，y，z，α，β，γ］。

由铰点分布图(图2)，用矩阵A 来表示上铰点Ai(i=1，2，…，6)在动坐标系中的坐标向量，用矩阵B 来表示下铰点Bi(i =1，2，…，6)在静坐标系中的坐标向量。

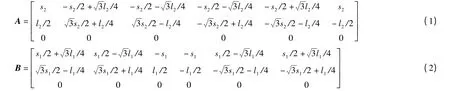
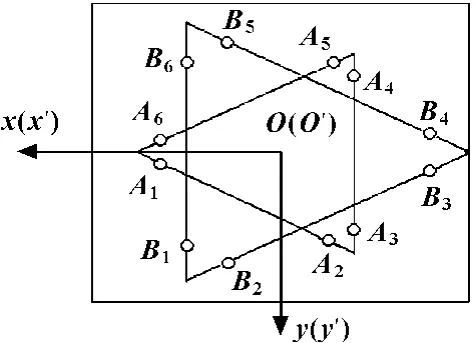
图2 铰点分布图

动平台在初始位置时，矩阵A 在两个坐标系的值完全一致，当其运动时，A 在动坐标系的值不变，在静坐标系中的值发生变化。上铰点在静坐标系的坐标向量用矩阵G 来表示，

其中T 为从静坐标系到动坐标系的变换矩阵:

活塞杆的伸缩量(即位移)可由上下铰点之间的实际距离减去初始长l0来确定。上下铰点间距离的计算公式为:

气缸活塞杆的伸缩量为:

3 平台虚拟样机

平台结构尺寸为:动平台铰链所在外接圆直径为450 mm，相邻铰点间距离为116.468 6 mm;静平台铰链所在外接圆直径为800 mm，相邻铰点间距离为138.918 5 mm;气缸直径40 mm，行程300 mm。平台所采用的是SMC 公司生产的CE1F40-300 型气缸，这种气缸的不回转杆上带有磁尺，缸体上装有检测传感器，外接计数器，行程可随时读出。

动平台的初始位置为中位，即6 个气缸同时伸出150 mm时的位置(气缸行程为300 mm)，此时，动静平台间的竖直距离为693.378 6 mm。在Pro/E 中装配完成的平台模型(负载质量30 kg)如图3所示。

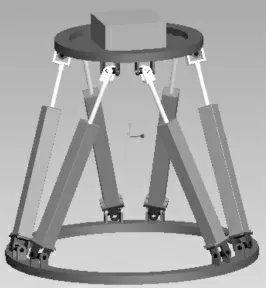
图3 六自由度运动平台装配图

将模型导入到ADMAS 中并添加约束，完成动力学仿真模型，效果图如图4所示。通过ADAMS 的模型校验工具检查模型，可以看到模型具有6 个自由度，没有冗余约束，模型校验成功。

图4 六自由度运动平台ADAMS 模型

4 比例阀控气动伺服系统

4.1 比例阀流量特性

在建立系统的数学模型之前，先做以下几点假设:

(1)工作介质为理想气体，即其性质及流动特性可统一用理想气体定律确切地描述出来;

(2)气体流经阀口及气缸运动时，气体的变化过程均为绝热过程;

(3)忽略泄漏。

则根据气体动力学有关理论，通过滑阀节流口的质量流量为:

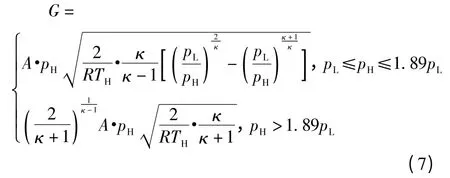
式中:pH、pL分别为阀的进出口压力;

κ 为绝热指数;

R 为气体常数;

TH为气体滞止温度;

A 为节流孔的有效开口面积。

4.2 气缸两腔压力微分方程

两腔的能量变化方程为:

式中:E 为气体内能，对于理想气体，E = CepV/R，Ce为气体等容比热，p、V 为容腔的压力和体积;

Qm为气体质量流量;

e 为单位质量的气体内能，对于理想气体e =CpT，Cp为气体等压比热;

Q 为气缸与外界传导的热量，由假设(2)，气体的变化过程均为绝热过程，因此dQ/dt=0;

W 为气体对外做的功，由W =pV，dW/dt 可以表示为pdV/dt;

设A1、A2为两腔截面积，v 为气体流速，L 为气缸工作行程，则无杆腔体积V1=A1vt，有杆腔体积V2=A2(L－vt)。

代入上式，整理得:

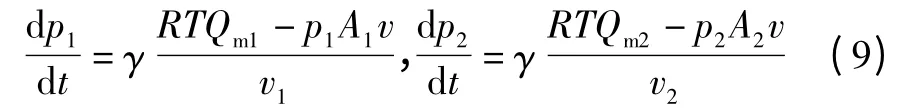
式中:γ 为气体定压比热Cp与定容比热Ce的比值。

4.3 气缸活塞力平衡方程

根据牛顿第二定律，可得:

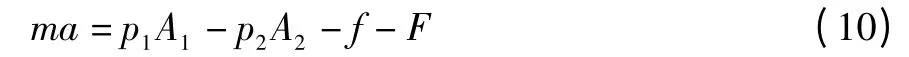
式中:f 为气缸摩擦力;m 为活塞和惯性负载的质量;F 为外力负载。

图5所示为在SIMULINK 中建立的比例控制气动伺服系统时域模型。

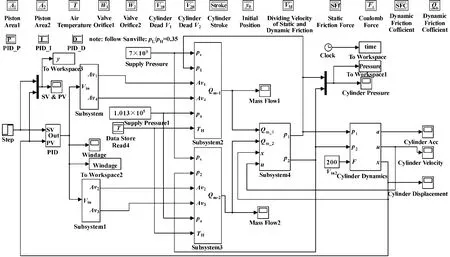
图5 比例控制气动伺服系统SIMULINK 模型

5 动力学仿真

在ADAMS 中，建立12 个变量，包括6 个气缸位移和6 个活塞杆受力(VARIABLEf_1、VARIABLEf_2、VARIABLEf_3、VARIABLEf_4、VARIABLEf_5、VARIABLEf_6)。在气缸缸体和活塞杆之间的圆柱副处添加直线驱动，定义直线驱动的输入值为6 个位移变量，然后将6 个受力变量取值为直线驱动的受力，这样就建立好了ADAMS 的输入和输出。

图6 MATLAB 与ADAMS 接口模块

利用Adams/Controls 模块，选择C++做为编译语言，将系统的控制参数导出为MATLAB 程序。在MATLAB 中运行生成的.m 文件并执行adams_sys，即可建立MATLAB 与ADAMS 的接口模块，如图6所示。

根据图1所示原理，将反解和气动伺服系统模块导入，连接完成的机械－气动联合动力学仿真系统模型如图7所示。

给定动平台姿态为绕z 轴的转动加沿z 轴的平动，转动的幅值是pπ/6，平动的幅值是50 mm，运行联合仿真，得到6 个气缸的位移曲线，如图8所示。可以看出，气缸基本能按设定轨迹运行，位置误差1 mm 左右。说明气压伺服式的运动平台是可行的。

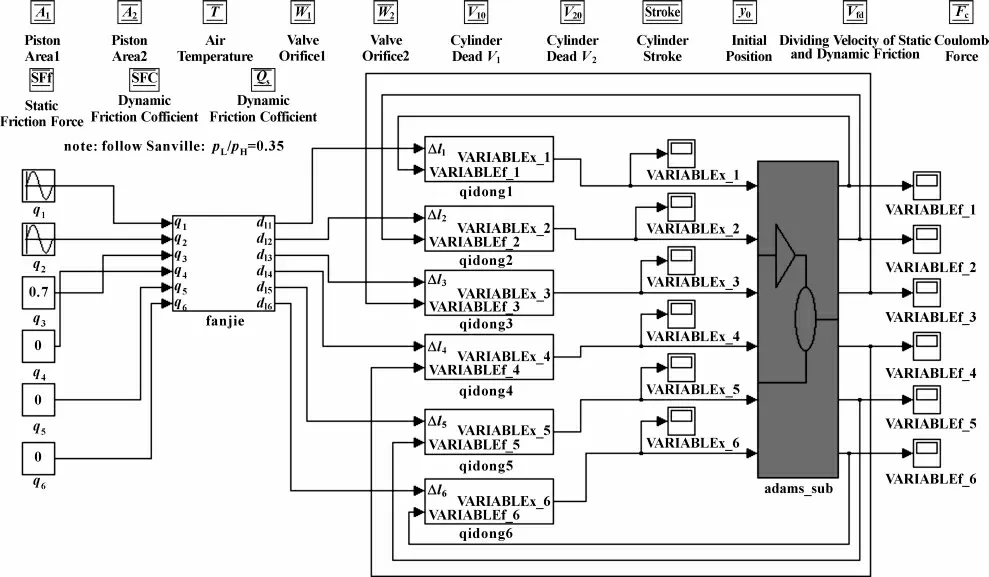
图7 机械－气动联合动力学仿真系统模型

图8 气缸位移曲线

6 结论

通过运用ADAMS 建立虚拟样机，避免了对并联机构进行繁琐的动力学分析和求解，考虑了气动系统的非线性，对气动伺服系统进行时域建模，完成了气压伺服式六自由度运动平台的动力学联合仿真，为平台的物理样机的制造奠定了理论基础。

从仿真的结果可以看出，气动式的六自由度平台的精度比液压式略低，但是响应速度较快，在轻载和对精度要求不高的场合，具有液压式所不具备的优势，并且可以降低设计和维护成本，减小污染，安全可靠。随着气压伺服技术的发展，气动式的六自由度运动平台必将拥有更广阔的研究和应用前景，并将更好地扩展气动技术与并联机构的应用领域。

【1】STEWART D.A Platform with Six Degree-of-freedom［C］//Proc.of the Institute for Mechanical Engineering，1965:371－386.

【2】黄真，孔令富，方跃法.并联机器人机构学理论及控制［M］.北京:机械工业出版社，1997.

【3】MAC CALLION H，PHAM D T.The Analysis of a Six Degrees of Freedom Work Station for Mechanized Assembly［C］//Proc.5th Word Congress on Theory of Machines and Mechanisms，1979:6－11.

【4】DASGUPTA B，MRUTHYUNJAYA T S.The Stewart Platform Manipulators:A review［J］.Mechanism and Machine Theory，2000，35(1):15－40.

【5】胡国才，侯志强，应朝龙.六自由度舰面模拟平台的数学建模与仿真［J］.海军航空工程学院学报，2006，21(3):307－310.

【6】陈聪，陈乐生.基于ADAMS 的六自由度运动平台运动学分析［J］.福州大学学报，2007，35(1):7－57.

【7】吴江宁，骆涵秀，李世伦.并联式六自由度电液伺服平台［J］.中国机械工程，1997，8(6):92－94.

【8】MERLET Jean Pierre.An Algorithm for the Forward Kinematics of General 6-DOF Parallel Manipulators［J］.Mechanism and Machine Theory，1990(12):4－6.

【9】杨灏泉，赵克定，吴盛林，等.飞行模拟器六自由度运动系统的关键技术及研究现状［J］.系统仿真学报，2002，14(1):84－87.

【10】GRAF R，VIERLING R，DILLMANN D.A Flexible Controller for a Stewart Platform［C］//Proceedings of the 1998 Second International Conference on Knowledgebased Intelligent Electronic Systems，1998:52－59.

【11】罗磊，莫锦秋，王时刚，等.并联机构动力学建模和控制方法分析［J］.上海交通大学学报，2005(1):75－78.

【12】BELSTERLING C A.Electrohydraulics Drives Flight Simulators［J］.Hydraulics ＆ Pneumatics，1984(2):37－40.