转子系统动静件碰摩故障的影响因素研究

华征潇，易风

（常熟理工学院机械工程学院，江苏常熟 215500）

转子系统动静件碰摩故障的影响因素研究

华征潇，易风

（常熟理工学院机械工程学院，江苏常熟 215500）

首先建立两自由度的转子系统碰摩的力学模型，而后采用Runge-Kutta数值方法进行仿真分析，主要研究转速变化时的时间历程、幅值谱和轴心轨迹.同时提取了转速和摩擦系数都发生变化时的振动特征，为有效诊断转子系统转静件碰摩程度提供了理论依据.

旋转机械；转速；碰摩；龙格库塔

碰摩是指旋转机械在转动过程中由于间隙不足造成的旋转件和静止件之间连续或间歇的接触行为[1].大型旋转机械，如汽轮发电机组动静件间碰摩故障时有发生，主要发生在机组动静叶片密封、转子轴封及滑动轴承等各个部位，为提高机组运行效率，常在动静件密封处调整间隙至较小，这就增加了动静件碰摩的可能性.研究表明，碰摩故障不同于转子不平衡、不对称等现象，它发生的时间短且位置不确定，因而难以检测和捕捉[2].国内外许多学者对动静碰摩做了大量的研究工作.文献[3]讨论了转子碰摩的稳定性；文献[4]利用傅氏级数分解说明了碰摩发生时不同谐波振动成分的来源；Bently和Ehrich[5]根据实验阐明了由于转子碰摩而产生的非线性运动；文献[6]利用数值积分方法对转子碰摩严重时的振动特征进行了初步分析；文献[7]对旋转机械动静碰摩的机理作了研究；文献[8]通过对转子局部碰摩故障的规律分析，介绍了碰摩故障的模糊诊断、灰色关联诊断及神经网络模型诊断的方法，并提出了一种新的转子碰摩故障模拟试验系统.研究表明转子动静碰摩故障属于典型的非线性振动故障.在实际工程中对于非线性振动问题的研究，一般有实验研究和理论研究，理论研究通常有数值方法、解析方法和几何方法等.本文首先建立二自由度的转子系统碰摩的力学模型，而后采用经典的Runge-Kutta数值解法对所建立的模型进行求解.

1 碰摩力学模型的建立

建立如图1所示的二个自由度的转子系统碰摩力学模型，该模型不计转轴质量，支承处弹性系数为Ks，阻尼系数为Ds.转子转动角速度为Ω，转子与定子的间隙为C，转静件偏心距用r0表示，转子质量为M，转子半径为ρ，转盘质量中心β与其几何中心O间距用rβ来表示，x、y为转子几何中心在任一时刻相对于定子几何中心在x、y方向的位移，转子系统绕z轴转动.

对上两式进行无量纲化可得

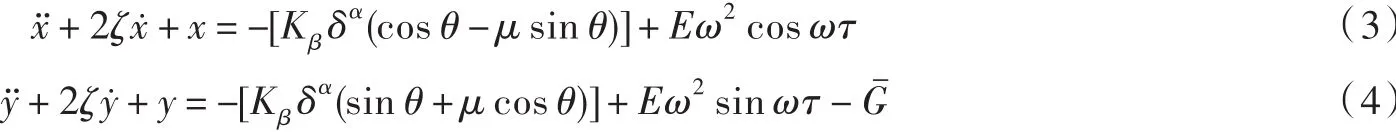
上两式中：

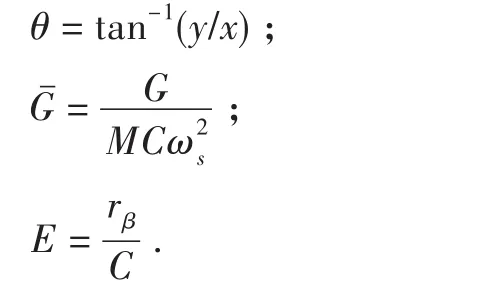
ζ—阻尼系数；

Ω—转子转速；

μ—摩擦系数；

α—变形指数；

Kβ—静子刚度.

2 数值仿真分析

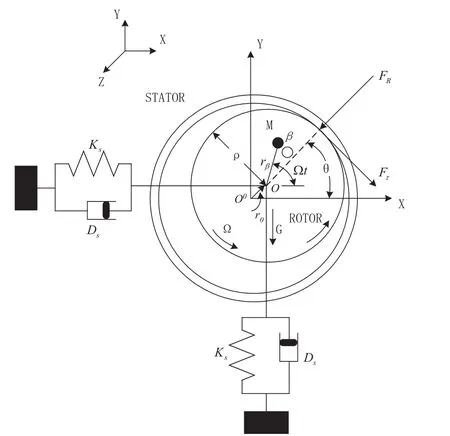
图1 转子碰摩的力学模型

对式（3）、（4）的非线性二阶微分方程进行降阶处理，将其转化为四个一阶的非线性微分方程组，然后在基于MATLAB平台下采用Runge-Kutta法对其进行数值积分.

各初始参数设置如下：

在其条件一定的情况下，通过改变参数转子转速Ω可以得到如图2的仿真结果.图2为无碰摩时的系统响应，其时域波形为正弦波，频谱图只有一个主要频率成份.轴心轨迹类似于椭圆.

随着转速的改变，振动也随之增加.出现了不同程度的碰摩故障.本文采集了三种不同转速下的系统响应（图3～图5）.

图2 转速为0.8398ωs时的系统响应

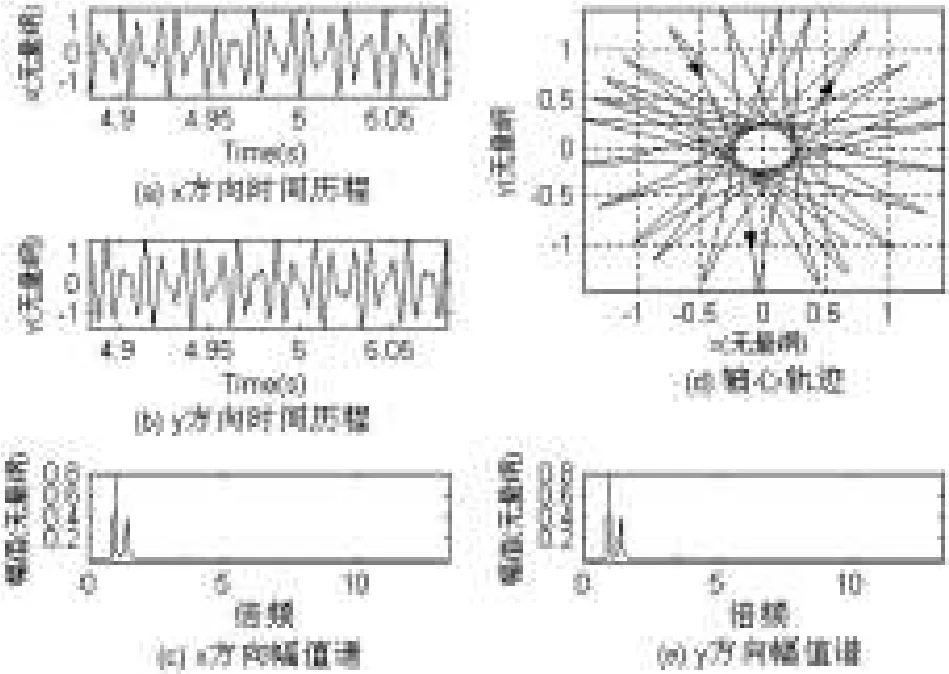
图3 转速为1.0954ωs时的系统响应

图4 转速为1.2926ωs时的系统响应

图5 转速为1.2945ωs时的系统响应

由图3～图5可知，当有碰摩发生时，其时域波形不再是有规则的正弦波.频谱图也出现了多个不同频率的振幅，带有多个频率成份.其轴心轨迹也明显不同.

图6～图8是在摩擦系数和转速同时改变时的特征图.在转速一定时，质量偏心距影响着振动的幅值：幅值越大，越容易发生碰摩；也影响着碰摩的程度.摩擦系数μ的大小关系到碰摩时碰摩切向力的大小，在摩擦系数较小时，由不平衡力引起的规则正进动在转子进动中起决定作用，在摩擦系数较大时，反向碰摩切向力可能使转子系统发生反向涡动，从而影响系统的稳定性.大量计算表明，随着摩擦系数μ的增加，保证转子稳定进动的Ωωn的范围减小.转子与定子的间隙对是否发生碰摩和碰摩的程度都有至关重要的影响.

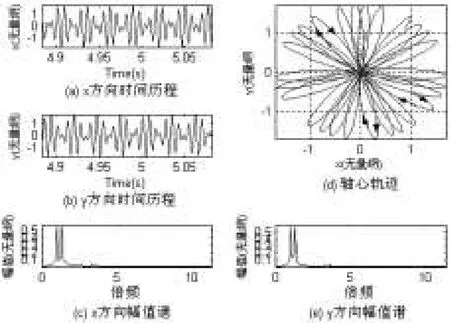
图6 摩擦系数μ=0.05、转速为1.2945ωs时的系统响应

图7 摩擦系数μ=0.06、转速为1.4369ωs时的系统响应

图9和图10是在不同转速下x、y方向振动信号傅氏变换组成的瀑布图.从瀑布图中可以看出，当碰摩发生时，开始出现高频分量，其中各倍频分量的附近还有一频率分量，这一系列分量无疑是由碰摩引起的，这里简称碰摩分量.随着转速的增加，碰摩分量在系统响应中所占的比例不断增加，而基频在系统响应中所占的比例相对减小，碰摩分量和基频分量之间频率间隔越来越小.当转速增加到某临界值时，两分量重合在一起，即引起转子系统的失稳.

改变系统参数，使μ=0.165，C=8×10-5m，Ds=1200 Nsm-1，转动角速度ω=250 rad/s，其他参数保持不变.得到图11所示的混沌运动.

3 结论

1）从振动信号时域波形特征的角度来分析：当转速较小时，没有发生碰摩故障，振动的时域波形为正弦波.当转子发生碰摩故障时，振动的时域波形发生畸变.

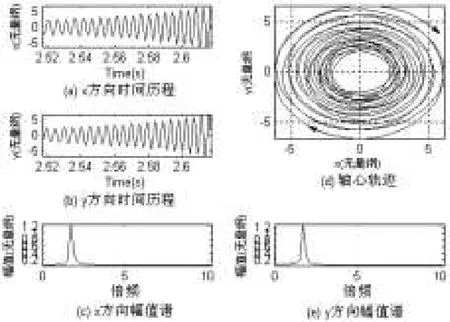
图8 摩擦系数μ=0.07、转速为1.4387ωs时的系统响应

图9 x方向振动信号傅氏变换瀑布图

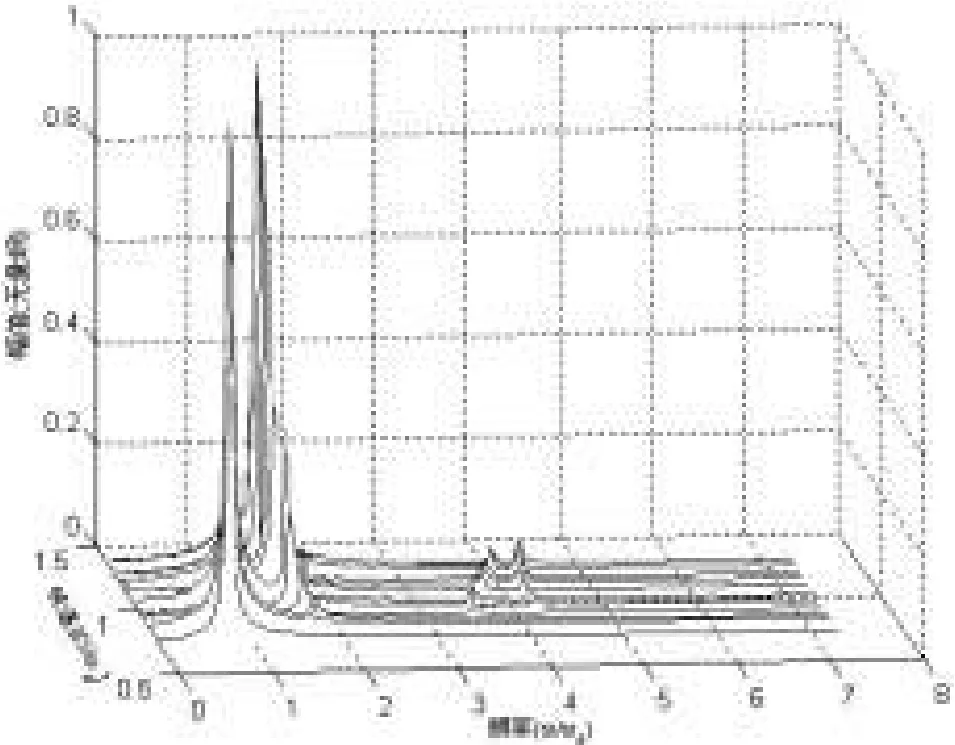
图10 y方向振动信号傅氏变换瀑布图

图11 混沌响应

2）从轴心轨迹的特征来分析：在转速较小时，转子系统在正常运转和轻度碰摩的情况下工作，轴心轨迹为一规则的圆或椭圆，见图2.但随着转速的增大，碰摩程度加深，轴心轨迹呈现花瓣形，见图3、4.随着转速的增加，会使轴心轨迹的拓扑结构发生变化，即转子系统发生失稳现象，轴心轨迹为多圆环缠绕，见图5.

3）频谱特征及分析：转子在正常运转情况下，其振动能量主要集中在与转速同频率的一次谐波（基波）上，其他频率的能量均很小.当转速较小时，系统振动也较小，因而系统未发生碰摩（转速小于0.8398ωs时，如图2所示）.由图6和图8知，在摩擦系数和转速由小到大变化时，反向碰摩切向力可能使转子系统发生反向涡动，从而影响系统的稳定性.由瀑布图图9和图10可知，当碰摩发生时，开始出现高频分量，其中各倍频分量的附近还有一频率分量，这一系列分量无疑是由碰摩引起的.随着转速的增加，碰摩分量在系统响应中所占的比例不断增加，而基频在系统响应中所占的比例相对减小，碰摩分量和基频分量之间频率间隔越来越小.当转速增加到某临界值时，两分量重合在一起，即引起转子系统的失稳.

4）振动性态分析：随着转速的增加，系统碰摩的程度在加深.分频、同频、倍频及其他一些频率成份的存在，是由于系统在转子转动频率和碰摩作用频率两者共同作用下的结果.假定转子转动频率为ω1，碰摩作用频率为ω2，则系统响应就有ω1±ω2、ω1±2ω2等频率成份出现.若这些信号成份的合成作用可以互相抵消，则整个系统响应表现为周期振动；若不可以互相抵消，则系统表现为拟周期振动.转子的运动一般要经历周期运动→拟周期运动→周期运动（摩擦系数μ较大时，在一定条件下还可发生失稳），一定参数下还可能出现混沌运动（见图11）.

5）各参数对系统响应的影响分析：模型对参数具有敏感依赖性，由图4和图5知，但转速从1.2926ωs增加到1.2945ωs时，转子系统从稳定状态跳跃到不稳定状态.可见转子转速对碰摩影响很大，此外，摩擦系数、质量偏心距和转子与定子的间隙等等对碰摩转子系统的动力学特性都具有显著的影响.

理论研究和实验研究已经表明，不同类型的碰摩故障和处于不同发展阶段的碰摩具有不同的故障特征，它们可以作为故障诊断的依据.然而这些仿真分析和研究结果与实际情况还有距离，因为相同的故障特征有可能对应着多种类型的故障，如质量不平衡、联轴节不对称、转子横向裂纹等，这些故障都会产生和碰摩故障类似的频谱特征.

其次，在对碰摩故障的监测诊断中，目前通常采用基于平稳过程的经典信号处理方法，根据碰摩的振动信号得到振幅、相位等特征频谱，传统的快速傅里叶变换（FFT）是长期使用的有效工具.但是，傅里叶变换需要假定信号在整个时间轴上是平稳的，也就是说它是从全局角度看信号的构成.当信号内含有局部信息时，使用傅里叶分析在一定程度上就失去意义，它不能反映出信号在时间局部区域上的频率特征，而这些局部化特征恰是故障的表现.碰摩过程中的摩擦和碰撞都具有高瞬态性，具有非线性特征，转子发生碰摩时的振动信号是含有丰富的高频、低频谐波分量的瞬态信号，所以，傅里叶分析对于碰摩故障的监测诊断不适用.显然，对于非平稳非正弦的碰摩故障动态信号，必须寻找能够反映时域特征又能够反映频域信息的新方法，才能提供故障特征全貌，正确有效地进行故障诊断.

[1]Sun Zhengce,Xu Jianxue,Zhou Tong.Analysis on Complicated Characteristics of a High-Speed Rotor System with Rub-Impact[J]. Mechanism and Machine Theory,2002,37(7):659-672.

[2]胡茑庆、张雨、刘耀宗，等.转子系统动静件尖锐碰摩时的振动特征试验研究[J].中国机械工程，2002，13（9）：23-26.

[3]Ehrich F F.Non-Linear Phenomena in Dynamic Response of Rotor in Anisotropic Mounting System.ASME[J].Journal of Mechanical Design,2012,117B:154-161.

[4]Choy F K,Padovan J.Non-Linear Transient Analysis of Rotor-Casing Rub Events[J].J Sound&Vibration,2007,113(3):529-545.

[5]Kim Y B,Noah S T.Bifurcation Analysis for a Modified Jeffcott Rotor with Bearing Clearances[J].Nonlinear Dynamics,1990,1(3): 221-243.

[6]岳国金，晏砺堂，李其汉，等.转子碰摩的振动特征分析[J].航空学报，2010，11（10）：499-502.

[7]戈志华，高金吉，王文永.旋转机械动静碰摩机理研究[J].振动工程学报，2003，16（4）：426-429.

[8]臧朝平，张思，许尚贤.转子局部碰摩故障的诊断方法[J].中国电机工程学报，2004，14（4）：50-56.

A Study on the Influence Factors of Rub-impact Fault in the Rotor System

HUA Zheng-xiao,YI Feng
(School of Mechanical Engineering,Changshu Institute of Technology,Changshu 215500,China)

This paper established mechanical model of rotor system’s rub-impact fault with two degrees of free⁃dom firstly,and conducted the simulation analysis with Runge-Kutta numerical method.The paper researched on time history,amplitude spectrum and orbit based on speed changes,got the vibration characteristics of speed and friction coefficient of common occurrence change,and provided theoretical basis for the effective diagnosis of rotor system’s rubbing degree.

rotating machine;rotational speed;Rub-impact;Runge-kutta

TK268

A

1008-2794（2013）04-0046-05

2013-04-09

华征潇，讲师，硕士，研究方向：基础力学，E-mail：huazhengxiao@cslg.edu.cn.